Abstract
The attack ratio in a subpopulation is defined as the total number of infections over the total number of individuals in this subpopulation. Using a methodology based on modified age-stratified transmission dynamics model, we estimated the attack ratio of COVID-19 among children (individuals 0-11 years) in Ontario, Canada when a large proportion of individuals eligible for vaccination (age 12 and above) are vaccinated to achieve herd immunity among this subpopulation, or the effective herd immunity with additional physical distancing measures (hence effective herd immunity). We describe the relationship between this attack ratio among children, the time to remove infected individuals from the transmission chain and the children-to-children daily contact rate, while considering the increased transmissibility of virus variants (using the Delta variant as an example). We further illustrate the generality and applicability of the methodology established by performing an analysis of the attack ratio of COVID-19 among children in the Canadian population. The clinical attack ratio, the number of symptomatic infections over the total population can be informed from the attack ratio, and both can be reduced substantially via a combination of higher vaccine coverage in the vaccine eligible population, reduced social mixing among children, and rapid testing and isolation.
1. Introduction
While the infection by the “Severe Acute Respiratory Syndrome-related Coronavirus type 2” (SARS-CoV-2) has been reported to affect all age-groups, including newborns and infants, children, adolescents and young adults (Gaythorpe et al., 2021), reliable and accurate epidemiological estimates of “Coronavirus disease 2019” (COVID-19) among children are particularly challenging to obtain (Hyde, 2021). The precise role of children in transmitting the pathogen has been controversial and a subject of debate (Gaythorpe et al., 2021; Hyde, 2021; Spielberger et al., 2021).
A recently published systematic review and meta-analysis (Gaythorpe et al., 2021) has synthesized 29 early studies of surveillance conducted during the first wave of COVID-19. Authors have found that the rate of children test-positive but clinically asymptomatic was 21.1%, whereas the rate of severely or critically symptomatic children was 3.8%. No studies on COVID-19 transmissibility in children could be retrieved, whilst susceptibility to COVID-19 among children was highly heterogeneous across studies included in the systematic review and meta-analysis. A recent study conducted in Norwegian families (Telle et al., 2021) has shown that young children can transmit COVID-19 virus to the same extent as adults. Available evidence is scarce, of poor quality and sometimes conflicting. However, cohort/population, network and household studies (Kim et al., 2021; Larosa et al., 2020; Li et al., 2020; Li et al., 2021; Macartney et al., 2020; Maltezou et al., 2021; Miller et al., 2021; Shah et al., 2021; Soriano-Ariandes et al., 2021; Yung et al., 2020) and meta-analyses of household surveys (Madewell et al., 2020; Xu et al., 2020; Zhu et al., 2021) seem to suggest that COVID-19 infection among children is generally asymptomatic or has a mild course, with “classical symptoms” such as cough, fever, anosmia and ageusia being less frequently reported with respect to nonspecific/gastrointestinal ones (Munro and Faust, 2020). However, as stated by Mehta et al. (2020) and by Hyde (2021), lower secondary attack rates in children may be due to the fact that children are less tested and exposed than adults. This seems more plausible than hypothesizing a biological difference in susceptibility. Some studies seem to confirm this reporting bias: Reukers et al. (2021) have applied a dense sampling approach in 55 Dutch households, with a total of 187 household contacts, computing a secondary attack rate of 35% among children. This rate is lower than the rate computed among adults (51%), but is considerably higher than the rate among children reported in previously published studies. On the other hand, some data seem to point to a shorter shedding period in children compared to adults, with an immunologically different response to the novel coronavirus in terms of antibody kinetics (Hyde, 2021; Mehta et al., 2020).
Moreover, previously reported epidemiological trends may be not updated in those settings and scenarios characterized by an increasing circulation of variants of the COVID-19 virus, such as the variant B.1.1.7 (also known as the Alpha variant). A recent study conducted in Germany (Loenenbach et al., 2021) found that secondary attack rate among children could be as similar as to the rate among adults. With children going back to schools, it is of paramount importance to compute the impact of re-opened schools on COVID-19 transmission dynamics. Sero-epidemiological surveys and contact tracing studies, such as the study conducted by (Boey et al., 2021), are needed, as well as mathematical models to inform and guide the decision-making process of public health decision- and policy-makers in terms of protocols and interventions to adopt and implement.
The present modelling study aimed at estimating the attack ratio among children, 0-11 years of age, when vaccination coverage alone or together with the implementation of some additional non-pharmaceutical interventions (such as use of face-masks or physical distancing) would enable the achievement of herd immunity. We here develop a methodology, based on analysis of a disease transmission dynamics model, to estimate the age-stratified attack ratio within a population. We then demonstrate the usage of this methodology by estimating the attack ratio of COVID-19 among children (specifically, individuals 0-11 years of age) in Ontario, Canada as a function of different adjustable model parameters, such as their activity levels and time to removal from the transmission chain. We explore the sensitivity of the attack ratio on these key parameters to gain insights into practical recommendation as to how to reduce this attack ratio of COVID-19 among children, which is key to ultimately reduce disease burden in this subpopulation while partially resuming social and economic activities. To illustrate the usage of the methodology in a different jurisdictional setting, we also provide a similar analysis of the attack ratio of COVID-19 for the entire country Canada.
2. Methods
2.1. The study setting and transmission dynamics model
We modified the transmission dynamics model (Tang et al., 2020), and its age-stratified analogue (McCarthy et al., 2020) to calculate the attack ratio of COVID-19 among children (0-11 years), defined as the total number of infected children over the total number of children in this age interval. We then estimated the model parameters according to the Canadian province of Ontario. We then estimated the attack ratio among children in Ontario against a variety of adjustable model parameters including the vaccine coverage and daily contact rate within the vaccine-eligible population (12 years of age and older), children-to-children daily contact rate (which we used as a proxy for school opening capacity), the testing and isolation of infectious individuals (potentially through contact tracing) considering the increased transmissibility of the Delta variant and decreased transmissibility through the utilization of masks and other physical distancing measures. As a demonstration of the generic methodology established, we also performed an analysis of similar scope for the attack ratio in Canada, based on specific features of the region reflected through different vaccination uptake and social mixing.
In our model, the population is divided into susceptible (S), exposed (E), asymptomatic infectious (A), infectious with symptoms (I), and recovered (R) compartments according to the epidemiological status of individuals. The population is further stratified by age, sub-index 1 for those eligible for vaccination (12 years and older) while sub-index 2 for children (0-11 years), so for example, S1 is the compartment of susceptible individuals eligible for vaccination, while I2 is the compartment for symptomatically infected children. The transmission dynamics model is given by a system of ordinary differential equations as follows:
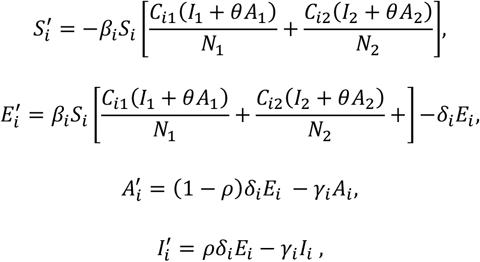for each age group i = 1,2. The model parameters, with the appropriate sub-indices (1 for vaccine eligible (12 + years), 2 for children (0-11 years), are defined as follows:
β: the transmission probability per contact;
θ: the relative infectiousness of asymptomatic infectious vs the symptomatic infectious;
δ: the inverse of the latent period;
ρ: the proportion of exposed individuals becoming symptomatic infectious;
γ: the rate at which the infected individuals are removed (recovery or isolation).
The contact mixing is described by:
C11: number of vaccine eligible-to-vaccine eligible contacts per day;
C12: number of vaccine eligible-to-children contacts per day;
C21: number of children-to-vaccine eligible contacts per day;
C22: number of children-to-children contacts per day.
N1 and N2 are the total number of vaccine eligible individuals and children, and S1(0) is the initial population of susceptible vaccine eligible individuals, and this is (given that the number of initially infected vaccine-eligible individuals is small) S1(0) = (1 − p)N1, with
p: the effective vaccine coverage, defined as the percentage of individuals in the vaccine eligible population vaccinated multiplied by the effectiveness of vaccination against infection.
2.2. The age-group specific attack ratio
By definition,the age group-specific attack ratio among vaccine eligible individuals and children are given by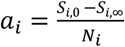 
, the difference of the initial and final size of the susceptible individuals in the population, divided by the total population. Through a mathematical analysis of the transmission dynamics model introduced in Section 2.1, we obtained a system of nonlinear equations which we solved to estimate the age-specific attack ratio (see Appendix A). Specifically, these were calculated by solving the coupled system of nonlinear algebraic equations (the so-called final-size equations) for x1 = 1 − a1, x2 = 1 − a2:
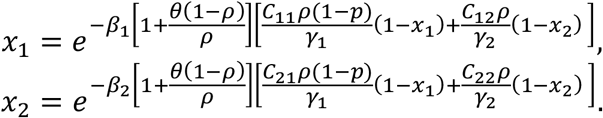
2.3. Non-VoC and VoC (the Delta variant) transmission rate
The baseline transmission rate β1 for the originally dominant strain (ancestral strain or non-VoC) was calculated from Ontario estimates assuming a baseline reproduction number R1,0 = 3.0 during the first wave among the vaccine eligible population. With pre-pandemic contact rates (c11 = 12.73), γ1 = 1/7, ρ = 0.7 and θ = 0.0275, the transmission rate β1 was computed by inverting the formula
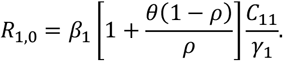
This calculation gave an estimated baseline transmission rate of β1 = 0.0466. To obtain the transmission parameters for the Delta variant, we assumed an increase in the transmissibility from the non-VoC to the Alpha variant by 1.4 (Volz et al., 2021; Davies et al., 2021) and an increased transmissibility by 1.6 from the Alpha to the Delta variant (Campbell, 2021; SPI-M-O, 2021), giving β1 = 0.1043, and we assumed that children are half as susceptible to infection by SARS-CoV-2 compared to the population of vaccine eligible (i.e., β2 = 0.05215). In the conclusion and discussion section, we will comment on how these baseline parameters can be adjusted and how the adjusted values change the calculated attack ratio in children.
2.4. Contact mixing in Ontario
We calculated the pre-pandemic contact mixing in Ontario and Canada, using the method developed in established work (McCarthy et al., 2020), updated to use the 2020 population data in Ontario and in Canada. We obtained the Ontario contact mixing matrix entries:
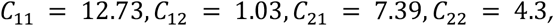and the mean connectivity was 13.5 daily contacts. The population profile for Ontario for the two age groups are N1 = 12,932,471, N2 = 1,801,543 (Statistics Canada, 2020). Similarly, we have for Canada the following:
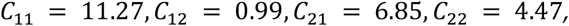and the mean connectivity was 12.14 contacts/day. The population profile for Canada for the two age groups are N1 = 33,198,268, N2 = 4,806,970.
2.5. Effective vaccination coverage
We computed the effective vaccine coverage by considering the protection granted by both the partial (1 dose) and full vaccination (2 doses) among individuals eligible for vaccination in the Ontario population as:
7% of coverage among vaccine-eligible (Government of Ontario, 2021) times 35% effectiveness against infection for single dose status = 0.07*0.35 plus
76% of coverage among vaccine-eligible (Government of Ontario, 2021) times 79% of effectiveness against infection for two dose status = 0.76*0.79,
which yields a total of 62.5% effective coverage for both vaccination statuses, as of August 27, 2021. The vaccine effectiveness against symptomatic disease for Delta for a single dose and two doses was estimated to be 35% and 79%, respectively (Public Health England, 2021). Hence, we here assumed that the vaccine effectiveness against infection is equal to vaccine effectiveness against symptomatic infection.
2.6. Simulation strategy and scenario analysis
We assessed the attack ratio according to different scenarios of the activity levels C11, C22 and the time to removal 1/γ1, 1/γ2. For this, we solved the system of nonlinear system of algebraic equations obtained in Section 2.2, the model parameters estimated in Sections 2.3 – 2.5 and the baseline parameter values listed in Table 1. Additionally, we assessed the time dynamics of the number of symptomatic and asymptomatic infections according to different values of 1/γ2 (3, 4, 5 days) by numerically solving the transmission dynamics model.
The parameter notation, description, baseline values and corresponding source are reported.
3. Results
3.3. Attack ratio among children and measures to reduce it
Using the methodology and parameter estimates established in Methods, we investigated a variety of scenarios to assess the impact of several adjustable model parameters on the attack ratio of COVID-19 among children 0-11 years of age in Ontario. Table 2 summarizes the numerical results when the activity among the vaccine-eligible population (C11) reaches its pre-pandemic level, namely, C11 = 12.73. We considered the value of γ1 = γ2 as 1/3, so infected individuals were assumed to be removed from the transmission chain (either through isolation or recovery) after three days on average, and varied the value of the children-to-children daily contact rate used here as a proxy for school opening capacity. The attack ratio decreased from 14.4% with the pre-pandemic children-to-children contact level (C22 = 4.3) to 9.2% and 6.4% when this contact is reduced by half or completely. With C11 = 12.73, the effective reproduction number in the vaccine-eligible population is 1.27 so the attack ratio of 6.4% in children is generated by an outbreak sustained by the vaccine-eligible population. To avoid an outbreak sustained by the vaccine-eligible population with about 62.5% effective vaccine coverage (see calculation above) for both single and double dose status, the activity level of the vaccine-eligible population must be below 10.02 contacts per day given the current parameter configuration.
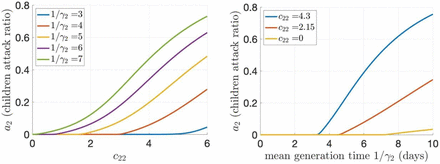
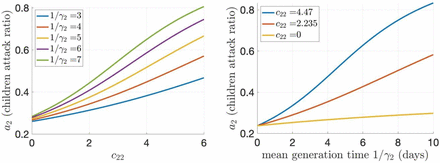
Figure 1 below provides additional information on the attack ratio in Table 2 (when C11 = 12.73). Specifically, the attack ratio a2 is explored with respect to different children-to-children daily contact rates, C22, and different values of the mean generation time 1/γ2 (Figure 1 left and right panels).
The attack ratio is depicted as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 3 and C11 = 12.73.
We also considered the activity level among the vaccine-eligible population C11 = 10 to avoid the outbreak sustained by the vaccine eligible population, approximately the activity level that was estimated in Ontario during its Stage 3 reopening in the 2nd wave (Wu et al., 2021). With C11 = 10, the attack ratio among children varies between 0.0368% with children-to-children level reaching its estimated pre-pandemic level, and this is reduced to 0.0115 when the children-to-children activity level is reduced by half (Table 3). The lower limit is 0.0068%, when the children-to-children contacts are reduced to zero (Table 3).
Figure 2 below provides additional information on the attack ratio in Table 3 (when C11 = 10). Specifically, the impact of social mixing and the time to removal from the transmission chain on the attack ratio is illustrated (Figure 2).
The attack ratio depicted as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 3 and C11 = 10.
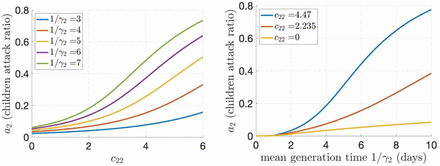
We also explored the significant role that rapid testing and isolation can play in determining the attack ratio among children 0-11 years in Ontario (Table 4). Here we fixed C11 = 10 as done previously, but assumed it takes 4 days, rather than 3 days used in Table 2 and Table 3, for an infectious individual to be removed from the transmission chain. The result is alarming; the attack ratio among children was estimated to reach 32.1% with full children-to-children activity and 13.1% even if all children-to-children contacts are eliminated in the limit case (Table 4).
Figure 3 below provides additional information on the attack ratio in Table 4 (when C11 = 10), in terms of its dependence on activity levels among children C22 and the mean generation time 1/γ2.
The attack ratio is assessed as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 4 and C11 = 10.
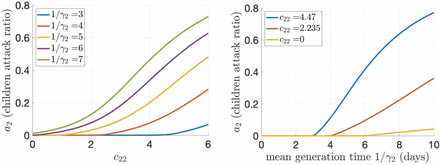
Similar to Table 4, Table 5 further illustrates the significant role that rapid testing and isolation can play. Here we fixed C11 = 10, but assumed it takes 5 days, rather than 3 and 4 days used in Table 2, Table 3 and Table 4, for an infectious individual to be removed from the transmission chain. The results are alarming; the attack ratio in children was estimated to reach 54.2% with full children-to-children activity levels and 27% even if all children-to-children contacts are eliminated in the limit case (Table 5).
Figure 4 below provides additional information on the attack ratio in Table 5 (when C11 = 10).
The attack ratio is shown as function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 5 and C11 = 10.
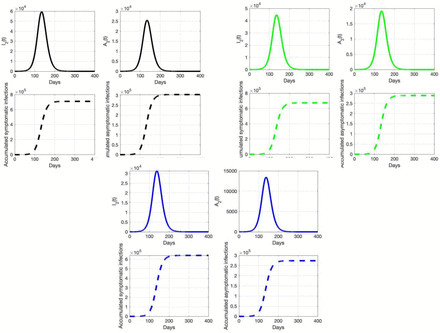
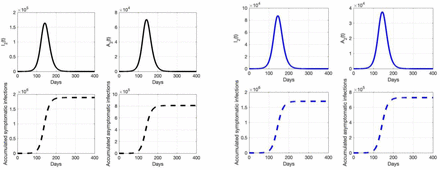
We also explored the time dynamics of asymptomatic and symptomatic infections as a function of the mean generation time (Figure 5). Specifically, Figure 5 below provides three epidemic curves as an illustration about the duration of an outbreak, the number of asymptomatic infections and symptomatic infections at the peak time, and the accumulated cases of COVID-19 in Ontario. We remark that the attack ratio is independent of the initial infections; but, the epidemic curves are impacted by the choices of initial conditions (Figure 5). For the similar analysis of the attack ratio of COVID-19 in Canada, see Appendix B.
Here the symptomatic and asymptomatic infections are assessed according to the configuration C22 = 2.15, C11=10, 1/γ1 = 7, for different values of 1/γ2 (black color for 5 days (top left), green color for 4 days (top right), and blue color for 3 days (bottom middle)). Initial infections for the vaccine-eligible are 100 and 10 for children 0-11 years of age.
4. Discussion and conclusions
Investigating the epidemiology of COVID-19 among children is of crucial importance in that it can inform relevant stakeholders in making informed decisions on how to devise and implement interventions aimed at preserving educational continuity and minimizing the disruption induced by the virus as much as possible.
In the existing scholarly literature, some mathematical models have simulated the effects of reducing children-to-children contacts. Abdollahi et al. (2020) devised an age-structured agent-based simulation model to simulate the effects of closing schools in Ontario, Canada, on the COVID-19 epidemic curve. The authors found that, without enforcing self-isolation of mild symptomatic cases, the impact was very limited, in terms of reduced intensive care unit (ICU) admissions. The burden imposed by the coronavirus was significantly reduced by the implementation of self-isolation practice. However, the precise effect of shutting/reopening schools may depend on the specific setting/country (Stage et al., 2021): in countries/territories where community transmission is low, school closing is a non-pharmaceutical intervention characterized by a limited impact, whereas it becomes more relevant in countries where community transmission is higher and more sustained. Some outbreaks have been, indeed, reported linked to school communities, for example, in Israel (Stein-Zamir et al., 2020), even though other observational studies could not find additional health risks generated by school reopening and in-person attendance (Aiano et al., 2021; Hershow et al., 2021; Mullane et al., 2021; Varma et al., 2021). All the previously mentioned mathematical models recommended to continue implementing non-pharmaceutical interventions, such as self-isolation and robust test-and-trace measures. This recommendation is particularly valid in those settings and scenarios characterized by an increasing circulation of variants of the COVID-19 virus, which have demonstrated increased transmissibility. In these settings, the computed secondary attack rate among children is not dissimilar to the rate among adults (Loenenbach et al., 2021).
There are several limitations to the analysis presented within. We here have assumed that individuals under the age of 12 are half as susceptible to infection by SARS-CoV-2 as those above 12 years. Future studies may explore sensitivity of the study results (e.g., the estimated attack ratio and its dependence on time to isolation and activity levels) in terms of the relative susceptibility between the two age classes. We here have assumed Delta has completely replaced the previously circulating strains, hence may slightly overestimate the transmission probability per contact as there are still a (relatively small) number of cases detected in Ontario associated with strains such as Alpha. We also assumed homogeneity among the two age classes which span large age groups: those individuals under 12 years and those individuals 12 years and above. The potential differences or heterogeneity in activity levels, susceptibility to infection by SARS-CoV-2 and vaccination coverage rates may be accounted for in subsequent studies.
In the present study, we have devised an algorithm to calculate the attack ratio among children under different scenarios of the activity level of the vaccine-eligible population and the children-to-children contact rate, and the speed in which infectious individuals are removed from the transmission chain. We remark that the algorithm is generic and therefore the attack ratio analysis presented within may be conducted for different geographic regions, which we have demonstrated in Appendix B by producing an analysis of similar scope for Canada. With the increased transmissibility of the Delta variant, a reduction from 12.73 to 10 contacts per day within the vaccine-eligible population in Ontario is necessary to avoid an outbreak sustained by the vaccine-eligible population due to lower vaccine coverage or vaccine efficiency against infection. With this contact level slightly higher than the estimated activity level during the Stage 3 reopening in Ontario (Wu et al., 2021), the attack ratio among children depends critically on how quickly infectious individuals are removed from the transmission chain, increasing from 3 to 4 and 5 days, meaning the attack ratio among children is estimated to increase from 0.0115% to 19.9% and 38.4% respectively.
Data Availability
All data used in the this study is publicly available and were openly available before the initiation of the study and can be accessed without application, or screening, or registration for access. All external data sources have been cited within and their source reported in the reference list. For verification purposes, the direct links for the dataset/web page which includes the vaccination coverage in Ontario, Canada and Canada used in the study are available at the links provided in the Data Availability Links. The two links provided are for the vaccination coverage in Canada dataset (Reference 40) and vaccination coverage in Ontario, Canada (Reference 30), provided in the form of an archive link to the web page live on August 27, 2021. Regarding the simulation code, inquiries can be directed to the corresponding author.
https://health-infobase.canada.ca/src/data/covidLive/vaccination-coverage-map.csv
https://web.archive.org/web/20210827212748/ https://covid-19.ontario.ca/data
Data accessibility
All data used for the simulations and analysis in this research are public and their source reported within. Regarding the simulation code, inquiries can be directed to the corresponding author.
Authors’ contributions
JW conceptualized the research. ZM and JD acquired the data to carry out the research. FS and JD performed the numerical simulations. JW, NLB, FS, ZM and JD contributed to writing the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This project has been partially supported by the Canadian Institute of Health Research (CIHR) 2019 Novel Coronavirus (COVID-19) rapid research program, and the Natural Science and Engineering Research Council of Canada (NSERC) and Public Health Agency of Canada (PHAC) Emerging Infectious Disease Modelling program for MfPH, Mathematics for Public Health. FS is supported by the UKRI through the JUNIPER modelling consortium [grant number MR/V038613/1].
Acknowledgements
JW is a member of the Ontario COVID-19 Modeling Consensus Table, and a member of the Expert Panel of the Public Health Agency of Canada (PHAC) Modeling group. FS is a member of INdAM Research group GNCS and of UMI Research group “Modellistica socio-epidemiologica”.
Appendix A: Calculating the final size and attack ratios
Let Si,∞ be the final size of susceptible populations (i = 1,2), namely, Si,∞ = Si,∞. Similarly, let Si,0 = Si (0). Integrating the equations for susceptible populations, we get
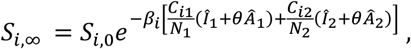where 
, and 
.
Using the equation for A and I, we get
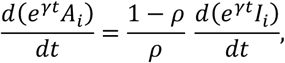from which we obtain
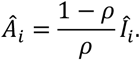
Substituting this into the equation for Si,∞ yields
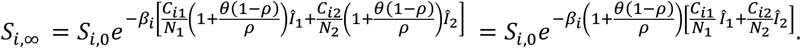
Finally, we observe that
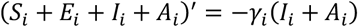
Therefore, we get
and
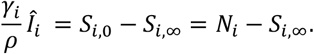
This leads to
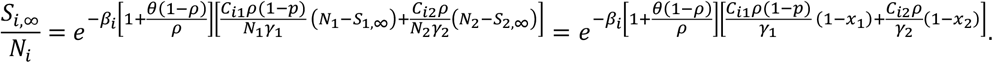
Appendix B: Analysis of the attack ratio among children 0-11 years of age in Canada
We here performed similar analysis as presented in the main text for the province Ontario as for the country Canada. Table B1 summarizes the results when the activity of the vaccine-eligible population reaches its pre-pandemic level, namely, C11 = 11.27. We considered the value of γ1 = γ2 as 1/3, so infected individuals can be removed from the transmission chain (either through isolation or recovery), and varied the value of the children-to-children contacts per day. The attack ratio decreases from 9.1% with the pre-pandemic children-to-children contact level to 4.4% and 2.3% when this contact is reduced by half or completely. With C11 = 11.27, the attack ratio 2.3% among children is generated by an outbreak sustained by the vaccine-eligible population. To avoid an outbreak sustained by the vaccine-eligible population with about 61% effective vaccine coverage for both single and double dose status, the activity level of the vaccine-eligible population should be below 10.02. We computed the effective vaccine coverage by considering the protection granted by both the partial and full vaccination as:
9.14% of coverage (Public Health Agency of Canada, 2021) times 35% of effectiveness (Public Health England) against infection for a single dose status = 0.0914*0.35 plus
72.99% of coverage (Public Health Agency of Canada, 2021) times 79% of effectiveness (Public Health England) against infection for a two dose status = 0.7299*0.79, which gives about 61% of effective coverage for all vaccinations.
Figure B1 below provides additional information on the attack ratio in Table B1 (when C11 = 11.27).
among children ages 0-11 years as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 3 and C11 = 11.27.
In Table B2, we considered the activity of vaccine-eligible population C11 = 10. With C11 = 10, the attack ratio among children varies between 0.17% with children-to-children level reaching its estimated pre-pandemic level, and this is reduced to 0.018% when the children-to-children activity level is reduced by half. The lower limit is 0.0091%, when the children-to-children contact is reduced to zero.
Figure B2 below provides additional information on the attack ratio in Table B2 (when C11 = 10).
among children 0-11 years as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 3 and C11 = 10.
Table B3 illustrates the significant role that rapid testing and isolation can play. Here we fixed C11 = 10, but assumed it takes 5 days, rather than 3 days used in Table B1 and Table B2, for an infectious individual to be removed from the transmission chain. The result is alarming, the attack ratio among children can reach 55.3% with full children-to-children, to 27.2% even if all children-to-children contacts are eliminated in the limit case.
Figure B3 below provides additional information on the attack ratio in Table B3 (when C11 = 10).
among children ages 0-11 years as a function of C22 (left panel) and 1/γ2 (right panel) for different values of 1/γ2 (left panel) and C22 (right panel) when 1/γ1 = 5 and C11 = 10.
Figure B4 below provides three epidemic curves as an illustration about the duration of an outbreak, the number of asymptomatic infections and symptomatic infections at the peak time, and the accumulated cases in Canada.
among children ages 0-11 years when C22 = 2.235, C11=10, 1/γ1 = 7, for different values of 1/γ2 (left panel in black color for 5 days, and right panel in blue color for 3 days). Initial infections for the vaccine-eligible are 100 and 10 for children.
References
