Abstract
Typically, mathematical simulation studies on COVID-19 pandemic forecasting are based on deterministic differential equations which assume that both the number (n) of individuals in various epidemiological classes and the time (t) on which they depend are quantities that vary continuous. This picture contrasts with the discrete representation of n and t underlying the real epidemiological data reported in terms daily numbers of infection cases, for which a description based on finite difference equations would be more adequate. Adopting a logistic growth framework, in this paper we present a quantitative analysis of the errors introduced by the continuous time description. This analysis reveals that, although the height of the epidemiological curve maximum is essentially unaffected, the position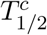 
obtained within the continuous time representation is systematically shifted backwards in time with respect to the position 
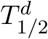predicted within the discrete time representation. Rather counterintuitively, the magnitude of this temporal shift 
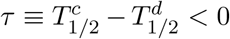is basically insensitive to changes in infection rate κ. For a broad range of κ values deduced from COVID-19 data at extreme situations (exponential growth in time and complete lockdown), we found a rather robust estimate τ ≃ −2.65 day−1. Being obtained without any particular assumption, the present mathematical results apply to logistic growth in general without any limitation to a specific real system.
Competing Interest Statement
The authors have declared no competing interest.
Funding Statement
The author received no funding for this research.
Author Declarations
I confirm all relevant ethical guidelines have been followed, and any necessary IRB and/or ethics committee approvals have been obtained.
Yes
The details of the IRB/oversight body that provided approval or exemption for the research described are given below:
This is a single-author paper. I am the only one entirely responsible for the content of this manuscript.
All necessary patient/participant consent has been obtained and the appropriate institutional forms have been archived.
Yes
I understand that all clinical trials and any other prospective interventional studies must be registered with an ICMJE-approved registry, such as ClinicalTrials.gov. I confirm that any such study reported in the manuscript has been registered and the trial registration ID is provided (note: if posting a prospective study registered retrospectively, please provide a statement in the trial ID field explaining why the study was not registered in advance).
Yes
I have followed all appropriate research reporting guidelines and uploaded the relevant EQUATOR Network research reporting checklist(s) and other pertinent material as supplementary files, if applicable.
Yes
Data Availability
All relevant data have been included in the manuscript.
