Abstract
The decline of active COVID-19 cases in many countries in the world has proved that lockdown policies are indeed a very effective measure to stop the exponential spread of the virus. Still, the danger of a second wave of infections is omnipresent and it is clear, that every policy of the lockdown has to be carefully evaluated and possibly replaced by a different, less restrictive policy, before it can be lifted. Tracing of contacts and consequential tracing and breaking of infection-chains is a promising and comparably straightforward strategy to help containing the disease, although its precise impact on the epidemic is unknown. In order to quantify the benefits of tracing and similar policies we developed an agent-based model that not only validly depicts the spread of the disease, but allows for exploratory analysis of containment policies. We will describe our model and perform case studies in which we use the model to quantify impact of contact tracing in different characteristics and draw valuable conclusions about contact tracing policies in general.
1 Introduction
The outbreak of COVID-19 presents a great challenge for governments and decision makers of the affected countries. To keep the number of infected people at a level the national health system can handle, a variety of different policies can be applied.
Most of these measures, such as closing schools, shops and restaurants proved to be effective in stopping the initial growth of the pandemic and lead to a decrease in the new infections per day. However, due to socioeconomic reasons lockdown policies can not be upheld long enough to eradicate the disease completely. After a certain time most of them have to be lifted again, while other measures have to be enforced to prevent a new upswing of the disease.
Contact tracing seems to be a viable method to keep the epidemic at bay. It allows to detect and isolate potentially infected contact partners even before they become infectious, leading to many successfully broken infection-chains. Yet, besides many successfully detected and isolated new infections, also a lot entirely unharmed contact partners would be put into preventive quarantine this way. The latter can be interpreted as the socioeconomic costs of tracing and should be minimised if possible.
Although stigmatised as a violation of personal freedom, tracing is not always related to personal-data-tracking devices like mobile apps. Successful tracing of contacts starts by isolation of household members or by temporarily closing workplaces of confirmed COVID-19 patients. Clearly, a lot of potentially infectious contacts can be traced by a simple patient-interviews as well.
Anyway, finding evidence that proves or quantifies the success of different tracing strategies is still difficult due to the novelty of the situation. In particular in Austria, as one of the first countries worldwide to overcome the peak of the disease [6], simulation models are basically the only opportunity to estimate the future impact of strategic changes. In this process, the TU Wien and the dwh GmbH closely collaborate with the Austrian Ministry of Health and the Federal Chancellery to provide at least a rough evidence for future policies via simulation models.
We developed an agent-based model (ABM) to reproduce the current outbreak of COVID-19 in Austria that allows for exploratory analysis of tracing in different characteristics. Aim of this work is to present this model and use it to evaluate and compare different tracing policies. We ask, whether containment of the disease can be achieved by successful tracing alone or if we need additional policies, and how we can quantify the benefits of tracing in general.
2 Methods
There is a large variety of simulation methods that allows for simulation of epidemics like SARS CoV-2, such as the classic differential equation based SIR model by Kermack and McKendrick [24]. Yet, as we are not only interested in the spread of the disease alone, but the evaluation of tracing policies, models that depict individuals are necessary. Consequently, an agent-based strategy was chosen. The model is comparable with similar models from Australia [15] and UK [16], but stands out by the following features:
It is based a very accurate spatial and demographic image of the Austrian population.
It utilises a contact network based on different locations, such as households, workplaces and schools.
It allows for tracing of agent-agent contacts and, consequently, for analysis of related tracing policies.
We explain our agent-based COVID-19 model based on the ODD (Overview, Design Concepts, Details) protocol by Volker Grimm et.al. [19,20]. The paper itself contains the Overview and the Design Concepts section, the Details section as well as a full list of parameter values and sources are found in the Appendix.
2.1 Overview
The dynamics of the agent-based COVID-19 model origins from the interaction of four modules.
Population Module. Altogether, the model is based on the Generic Population Concept (GEPOC, see [13]), a generic stochastic agent-based population model of Austria. It validly depicts the current demographic as well as the regional structure of the population on a microscopic level. The flexibility of this population model makes it possible to modify and extend it by almost arbitrary modules for simulation of population-focused research problems.
Contact Module. In order to develop a basis for infectious contacts, we modified and adapted a contact model previously used for simulation of influenza spread. This model uses a distinction of contacts in different locations (households, schools, workplaces) and is based on the POLYMOD study [30], a large survey for tracking social contact behaviour relevant to the spread of infectious diseases.
Disease Module. We implemented a module for the course of the disease that depicts the current disease-pathway of COVID-19 patients starting from infection to recovery and linked it with the prior two modules.
Policies Module. A module for implementation of interventions, ranging from contact-reduction policies, hygienic measures and, in particular, contact tracing. This module can be imagined as a timeline of events at which certain policies are introduced or lifted.
2.1.1 Purpose
The agent-based COVID-19 model aims to give an idea about the potential impact of certain policies and their combination on the spread of the disease, thus helping decision makers to correctly choose between possible policies by comparing the model outcomes with other important factors such as socioeconomic ones. In order to fulfil this purpose, it is crucial that the agent-based COVID-19 model validly depicts the current and near future distribution and state of disease progression of infected people and their forecasts.
2.1.2 Entities and State Variables
The model essentially contains only one class of agents, which we also call person-agents. Each person-agent models one inhabitant of the observed country/region. We describe state variables of a person-agent sorted by the corresponding module.
Population Module. Each person-agent contains the population specific state variables sex, date of birth (≅ age) and location. The latter defines the person-agent’s residence in form of latitude and longitude and uniquely maps to the agent’s municipality, district and federal state.
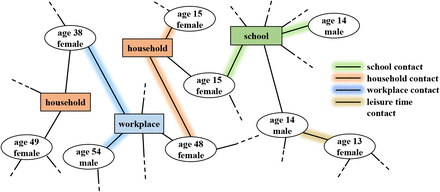
Contact Module. The person-agent features a couple of contact network specific properties. These include a household and might include a workplace or a school. We summarise these as so-called locations which represent network nodes via which the person-agent has contacts with other agents. Assignment of person-agents to locations is based on distance of the agent’s residence to the position of the location. Each day, an agent has a certain number of contacts within each of its assigned locations, which leads to spread of the disease. To model contacts apart from these places, every person-agent has an additional amount of leisure time contacts, which are sampled randomly based on a spatially-dependent distribution. The contact network is schematically displayed in Figure 1.
Contact network of agents in the agent-based COVID-19 model. Regular contacts between agents occur via locations (schools, workplaces and households), while random leisure time contacts extend the standard contact network.
Disease Module. To model the progression of the disease, each person-agent has a couple of states that display the current disease/health status of the agent. They are infected,, infectious, symptoms, hospitalised,, critical, confirmed, severe, asymptomatic, home-quarantined and recovered. These states can either be true or false, multiple of them can be true at a time and they enable or disable certain person-agent actions. The influence of these state variables and how they change is described in Section 2.1.4.
Policies Module. Policies either affect locations or person-agent-behaviour directly and require additional agent properties. All locations except for households are defined open or closed which marks whether this place is available for having contacts. For person-agents the state preventive quarantine is introduced which marks agents isolated due to tracing.
We address mentioned parameters as attributes for the corresponding agents, i.e. an agent whose infectious state is true is termed as “infectious agent”.
2.1.3 Scales
Unlike other ABMs the model cannot be run with a scaled-down number of agents, e.g. one agent representing 10 or 100 persons in reality. This is due to the problem that an agent’s contact-network cannot be scaled this way. Consequently, one simulation run always uses agents according to the size and structure of the actual population in the country/region.
2.1.4 Process Overview and Scheduling
Like the underlying population model, the agent-based COVID-19 model can be interpreted as hybrid between a time-discrete and a time-continuous (i.e. event-updated) ABM:
The overall simulation updates itself in daily time steps, wherein each step is split into three phases. In the first phase, the planning phase, each agent is called once to plan what it aims to do in the course of this time step. In the second phase, each agent is, again, called once to execute all planned actions for this time step in the defined order. In the third step, a recorder-agent keeps track of all aggregated state variables.
On the microscopic scope each person-agent is equipped with its own small discrete event simulator. In the mentioned planning phase, each agent schedules certain events for the future which may, but not necessarily must, be scheduled within the current global time step. In the second phase, the agent executes all events that are scheduled for the currently observed time interval, but leaves all events that exceed this scope untouched.
This strategy comes with a couple of benefits. First of all, in contrast to solely event-based ABMs, the event queue is distributed among all agents which massively increases the speed for sorting (a solely event-based ABM with millions of complex agents would not be executable in feasible time). Moreover, in contrast to solely event-based ABMs, usage of daily transition probabilities/rates instead of transition times is possible as well. Finally, in contrast to solely time-discrete ABMs, agents can operate beyond the scope of time steps and sample continuous time-intervals for their state-transitions.
We shortly describe all actions that are scheduled and executed by one person-agent within one time step sorted by the specified module.
Population Module. As briefly described in [13], agents trigger birth and death events always via time- and age-dependent probabilities that apply for the observed time step (i.e. the observed day). Note that in contrast to the basic population model, immigration and emigration events are disabled in the agent-based COVID-19 model due to closed borders in reality.
Contact Module. Also contact specific events are scheduled and executed within the scope of only one time step: First of all, the agent schedules a contact event with every other member of its household. Moreover, if such a location is present in the contact network, a certain number of workplace or school contacts, respectively, are scheduled and corresponding partners drawn randomly from the assigned location. Finally, a certain number of leisure time contacts are sampled and partners are drawn based on a region-specific distribution: a leisure time contact partner is drawn uniformly from the same municipality with probability pm, from a different municipality within the same district with probability pd, from a different district in the same federal state with probability pf, and finally, from a different federal state with probability pa.
As mentioned, some states limit the agents’ capabilities of interaction. Quarantined or preventive quarantined agents have no random leisure time contacts and no contacts at work or school. Furthermore, hospitalised agents do not even contact their household members. The impact of potentially infectious contacts to hospital personal is neglected as it lies outside the scope of the model.
Disease Module. First of all, it is important to mention that the model is not parametrised by a reproduction number R0 or Reff, but by a contact specific probability. Nevertheless, the ABM provides the opportunity to carry out estimates for R0 and Reff as model output. This is done using the original definition of these epidemic parameters: the average number of secondary infections of an infected agent.
Anyway, in case of an aforementioned contact, infectious agents spread the disease to susceptible agents with a certain infection probability which triggers the start of the newly-infected agent’s disease-pathway. This pathway describes the different states and stations an agent lives through while suffering from the COVID-19 disease and can be interpreted as a sequence of events of which each triggers the next one after a certain sampled duration.
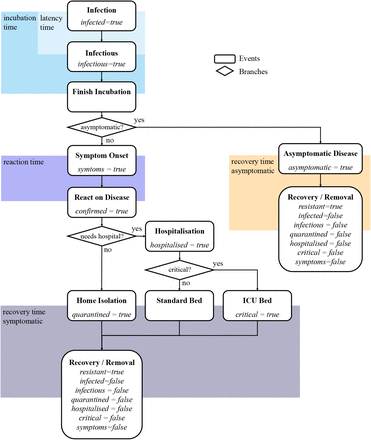
We show this infection strategy in a state chart in Figure 2 and describe how to interpret this figure by explaining the initial steps in the pathway in more detail: As soon as the “Infection” event is executed for a person-agent, its infected state is set to true and a latency period is sampled according to a specific distribution. The corresponding “Infectious” event is scheduled for the sampled period in the future. As soon as this “Infectious” event is executed, the infectious parameter is set to true and a random process decides whether the person will develop symptoms or not. This point marks the first branch in the patient’s pathway and whether the “Symptoms Onset” event or the “Asymptomatic” Event is scheduled. The prior would be planned after a sampled time span corresponding to the difference between latency and incubation time, the latter would be triggered instantaneously. All other elements of the pathway follow analogously.
Finally, it is important to clarify that the model does not specifically consider deceased agents as this is not within the scope of the model (see Section 4.3). Consequently, any recovered agent can be considered as either immunised or deceased.
Policies Module. Policies are timed events that can be fed into the model as a timeline. Every policy input is then interpreted and scheduled as a global timed-event and executed in the course of the corresponding simulation time-step. The elements of this timeline may include the following policies:
Close/Open Location. The model classifies a fraction of locations of a certain type as closed (except household) and makes them unavailable for contacts.
Reduce Contacts. Agents reduce the daily number of contacts within a certain location or in leisure time by a scaling factor. This policy can be parametrised to reduce leisure time contacts for all or only for agents within a certain age-class.
Increase Awareness. Person-agents start to react more quickly to their symptoms and reduce their reaction time, i.e. the time between symptom onset and becoming confirmed and isolated.
Hygienic Measures. At specific locations the infection probability is reduced.
Location Tracing. Locations are closed precautionarily, if one of its assigned person-agents becomes confirmed.
Individual Tracing. A certain fraction of agents record their contacts. If the agent becomes confirmed, the traced contacts become isolated precautionarily.
State chart of the patient pathway of a person-agent in the agent-based COVID-19 model. Only those state variables that are changed by the corresponding event are labelled, all others remain at the current value. The initial state of all infection-specific state variables is false.
2.2 Design Concept
2.2.1 Basic Principles
In order to fulfil the modelling purpose, the ABM is designed as simple as possible yet depicting the most important features for evaluation of policies. Consequently, lots of details within the pathway of an infected person and, in particular, lots of details within the personal daily routine are simplified to avoid indeterminable model parameters and unpredictable model dynamics.
2.2.2 Emergence
In addition to the classic emergence of nonlinear epidemiological effects it is one of the key objectives of the model to analyse the effects of interplay of different measures. Hereby, seemingly unconnected policies like school closure and contact reduction for the elderly might lead to surprising effects when applied simultaneously. More generally speaking, the model displays that the individual effects of applied policies do not add up linearly.
2.2.3 Sensing
Agents’ perception is one of the key problems of modelling COVID-19. In the agent-based COVID-19 model, three levels of perception are distinguished:
Perception of the individual. First of all, no agent is actually aware of its own disease and, more importantly, infectiousness before symptoms occur. Therefore, agent parameters can be distinguished into two sets: the ones the agent is aware of (e.g. symptoms, hospitalised), and the ones it is not (e.g. infected, infectious).
Perception of the general public. Within the reaction time period agents already know about their illness (they have symptoms), yet, the COVID-19 case is not yet confirmed and the case does not appear into the national statistics. So, the general public is not aware of this case.
Perception of the omniscient observer. Finally, an omniscent observer is able to track, but not influence, anything that happens within the model (see Section 2.2.6).
Consequently, the levels of perception can be sorted with regards to their amount of knowledge:
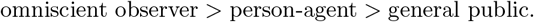
These three levels seem insignificant, but make it possible to validly parametrise the model via data with reporting delay.
2.2.4 Interaction
Interaction between agents only occurs in form of contacts at locations or during leisure time. The features provided by the underlying population model make it possible to investigate contacts on a very local level. As described before, leisure time contacts are weighted by their regionality. Also school and workplace contacts are biased locally as the corresponding locations are assigned person-agents via distance-dependent probabilities (see Section 6.1.1). Consequently, interactions between agents follow a spatially-continuous locally-biased contact network.
2.2.5 Stochasticity
Basically all model processes, including the initialisation, contain sampling of random numbers. Therefore, Monte Carlo simulation is applied, results of runs are averaged and their variability is assessed (see Section 6.2).
2.2.6 Observation
As mentioned, a “recorder agent” takes care of tracking and aggregating the current status of the simulation. At the end of each global time step, all person-agents report to the recorder agent which furthermore keeps track of all necessary aggregated model outputs. This includes for example confirmed cumulative cases, hospitalised agents, asymptomatic agents, pre-symptomatic agents, recovered agents, agents in a certain hospital, or averagenumber of contacts per infectious agent. For the specified tracing scenarios the confirmed active cases and preventive quarantined agents are the key observables of the model.
2.3 Details
We only give a rough overview of the model initialisation and calibration process. For more specific model details (third pillar of the ODD protocol), we refer to the appendix, in specific, Section 6.1.
2.3.1 Initialisation
In order to start the simulation at the specified time t0, publicly available data, i.e. the reported total number of positive tests and current data for hospitalisations, are not sufficient, especially, as the majority of the new infections are caused not by the detected but the undetected persons.
Consequently, an initialisation phase validly simulates the progress of the disease from a fictional 40 newly infected agents in February until to. For a more technical information about this initial phase, we refer to the Appendix (Section 6.1.2).
Anyway, the initialisation phase is calibrated to depict the correct doubling rates of the confirmed cases before introduction of policies as well as the positive impact of the lockdown.
2.3.2 Calibration
To successfully calibrate the model to the real timelines, a bisection method is used that allows us to adjust one parameter at a time.
In particular this refers to the infection probability which is fitted to the time before lockdown. The lockdown-policies and their parametrisations are partially calibrated to fit the observed flattening of the curve and partially abstracted from real policies made in Austria. For example, nationwide closure of schools is modelled as such: the location type school becomes unavailable for contacts.
For more information on the calibration process, the reader is referred to Section 6.1.4.
2.4 Model Implementation
The simulation of ABMs like the specified agent-based COVID-19 model is a huge challenge with respect to computational performance. As the model cannot be scaled down, almost 9 million interacting agents need to be included into the model in order to simulate the spread of the disease in Austria.
These high demands exclude most of the available libraries and software for agent-based modelling including AnyLogic [18], NetLogo [34], MESA [27], JADE [11] or Repast Simphony [31]. Most of these simulators cannot be used as their generic features for creating live visual output generates too much overheads.
Consequently, we decided to use our own agent-based simulation environment ABT (Agent-Based Template, see [3]), developed in 2019 by dwh GmbH in cooperation with TU Wien. The environment is implemented in JAVA and specifically designed for supporting reproducible simulation of large-scale agent-based systems. Technical details are found in the appendix, Section 6.2.
2.5 Scenario Definitions
In this section, we briefly describe the simulation scenarios, we used to analyse the impact of tracing policies. For detailled parameter-tables of the scenarios, we will partially refer to the Appendix.
First of all, we chose April 9th 2020, 08:00 AM as our initial time of the simulation – we will henceforth denote this time by t0. By this time, countrywide lockdown in Austria had already managed to reduce Reff, the effective transmission rate of the disease, below 1 causing the number of newly infected people per day to decrease. About 12900 positive virus tests had been reported until this date1.
2.5.1 Scenario: Initialisation Phase until t0
The country realised nationwide closure of schools and workplaces on March 16th, yet our calibration process revealed that this lockdown should rather be modelled as a process with several steps, which are briefly listed in the appendix in Table 7. It is clear that the modelled policy events and, in particular, their parametrisation cannot be taken into account separately – some of them might have a larger, some a smaller impact in reality than the model – yet the summary of all policies allowed us to calibrate the current curve of the disease by feasible and causally-founded assumptions.
2.5.2 Scenario: Baseline
To create a reference, we established three fictional baseline scenarios, a high, a medium and a low compliance scenario, that simulate the further course of the epidemic. They start from to (April 9th 2020) under the ongoing lockdown policies and consider the subsequent lifting of the implemented measures. In all three fictional baseline scenarios, the lockdown policies are almost fully lifted on May 1st. Contacts in schools, workplaces and households are back on the basis level and only the leisure time contacts are slightly reduced. Hereby, the compliance is varied by different assumptions of the population to maintain leisure time hygiene standards (distancing) and quantity of leisure time contacts:
high compliance: Leisure time infection probability is reduced by 50%, contact numbers are reduced by 75%.
medium compliance: Leisure time infection probability is reduced by 50%, contact numbers are reduced by 50%.
low compliance: Leisure time infection probability is reduced by 50%, contact numbers are not reduced at all.
A detailed specification of the three scenarios can be found in the appendix in Table 8.
We want to emphasise that all baseline scenarios defined here are entirely fictional and they do not and are not designed to represent the current and future situation in reality. For example, they do not include school closings during the summer or other holidays, and weekends are not considered either. Furthermore, we assume an unlimited testing capacity such that, even at the height of the epidemic, all symptomatic persons can be tested without increasing the reaction time between symptom onset and becoming a confirmed case. Yet, the scenarios allow to solely focus on the specific impact of tracing related policies without any other disturbances. In particular, they are chosen so that none of the tracing policy scenarios instantaneously pushes Reff below the critical point 1. Having such a bifurcation within the parameter study would make it impossible to compare any two scenarios quantitatively.
2.5.3 Scenario: Location Tracing
The first measure to be evaluated by the simulation model are location tracing policies. We define this policy as the reaction of a person’s direct surrounding in response to a positive COVID-19 virus test result. While isolation of the affected person is done as usual, now also all persons in the direct surrounding of the infected person will become isolated as well, independent of their current disease state. In this process, the surrounding is defined as the group of persons that commonly visit the same locations as the infected person. By this measure we expect to find and isolate a high percentage of infected persons before they even become visible to the system.
In the model, we studied the effects of location tracing regarding two location types: household and workplace. The policy household tracing means that as soon as an agent enters the confirmed status, all other members of the agent’s household are isolated as well. In workplace tracing, the workplace of a confirmed COVID-19 patient is temporarily closed and all the coworkers are put into preventive quarantine.
In isolation, agents only have contacts with the other members of their household. They do not attend school or work and do not have leisure time contacts. After a fixed number of days - we chose 14 days for our scenarios - agents are released from isolation and can resume their normal behaviour, if they turn out to be unaffected by the virus. Clearly, the availability of a precise test could reduce the required quarantine length, yet this feature is not included in the model thus providing conservative estimates.
We evaluated the impact of the location tracing for households and for workplaces separately as well as in combination, henceforth denoted as combined tracing scenario. In the simulation, the policies have been implemented on May 15th, a time at which the new upswing of the epidemic can already be observed by an increasing number of new infections.
2.5.4 Scenario: Individual Tracing
Extending the ideas of location tracing we studied the effects of individual tracing of contacts. For this tracing policy, we assume that a certain amount of people record their contacts outside of their household, for instance by using a tracing app on their smartphone or on a similar device. In this process, a contact is recorded if both involved persons use the tracing device. We assume that the tracing is completely accurate. In this way, all contacts between persons using the tracing device are recorded and, most importantly, there is no infection between two tracing people that goes undetected. These contacts are saved for a specific recording period. If a person using the tracing device becomes a confirmed case of COVID-19, the recorded contacts are informed and placed under preventive quarantine. The implications of the preventive quarantine are the same as in Section 2.5.3.
The effectiveness of this policy has been evaluated on top of the location tracing policies for households and workplace contacts, i.e. the combined tracing scenario. We considered rates of 50% and 75% of people using the tracing device and a recording period of 7 days. The length of the preventive quarantine is fixed at 14 days and the implementation date is May 15th, the same as the policies from Section 2.5.3.
3 Results
3.1 Initialisation Phase until t0
Although not directly related with tracing policies, we first want to give an image of the results of the initialisation phase defined in Section 2.5.1.
On the average, by March 16th, the modelled total contacts per day were reduced by about 78%, with additionally reduced infectivity of contacts at workplace and in leisure time by 50%. As mentioned in the model description, the calibrated model provides the opportunity to carry out estimates for the reproduction numbers Reff and, most importantly, R0. The fitted model results indicate R0 ≈ 4.5.
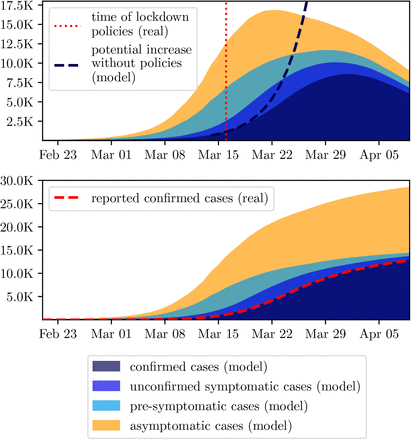
Figure 3 depicts the results of the initialisation phase. It nicely displays that the confirmed cases are only one part of the total infected population and that it is necessary to consider all of them to generate a feasible initial population at t0: the asymptomatic, that never feel any or only mild symptoms and remain undetected, the pre-symptomatic, that are still within the incubation period, and the unconfirmed symptomatic, that have not yet reacted on their symptoms or wait for being tested.
Comparison of the initial phase and reported data from Austria. Upper plot shows active cases while the lower plot displays cumulative.
3.2 Baseline Scenarios
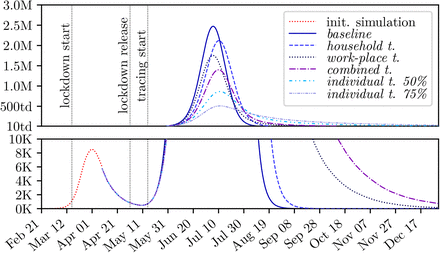
In the three baseline scenarios high, a medium and low compliance, defined in Section 2.5.2, a new upswing of the disease occurs around 14 days after the lifting of the lockdown policies. In the scenario with the low compliance, the epidemic reaches a peak of around 2.47 million confirmed cases (28% of the population) approximately 9 weeks after the end of the lockdown. In total, the model contained 4.25 million confirmed agents (47% of the population) and 8.5 million infected agents (95% of the population), which includes asymptomatic and pre-symptomatic agents as well.
In the scenario with the medium compliance, the peak of the confirmed cases is reached around 11 weeks after the lifting of the lockdown policies with a value of 1.86 million agents (21% of the population). At the end of the pandemic, there has been a total of 3.87 million confirmed cases (43% of the population) and 7.74 million infected agents, which accounts for 86% of the population. The reduction of the leisure time contacts in the scenario with the high compliance lead to a 26% reduction for the peak of the epidemic compared to the scenario with low compliance.
In the scenario with the high compliance, the epidemic reaches a peak of 1.43 million confirmed agents (16% of the population) 12 weeks after the lifting of the lockdown policies. Around 3.44 million agents (38% of the population) were confirmed in total, 6.88 million agents were infected (77% of the population). The further reduction of the leisure time contacts managed to reduce the peak of the epidemic by 42% compared to the scenario with low compliance.
The simulated timelines for the confirmed agents of the baseline runs are displayed in Figure 4.
Simulation of the baseline scenarios high, medium and low compliance. The plot is split into two parts to allow a detailed image of the different scales without logarithmic scaling.
3.3 Location Tracing
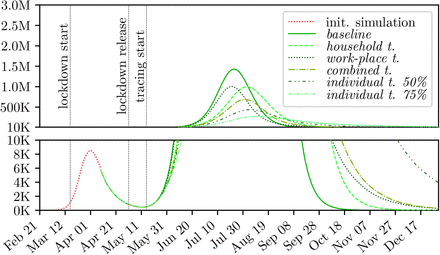
The results of the three location tracing scenarios household workplace and combined tracing, defined in 2.5.3, can be seen in Figures 5, 6 and 7, and Table 1, respectively.
Comparison of different tracing policies for the low compliance baseline.
Comparison of different tracing policies for the medium compliance baseline.
Comparison of different tracing policies for the high compliance baseline.
Simulation results for location tracing policies.
To evaluate the policies, we considered the reduction of the peak of the active confirmed cases as well as the peak of the agents currently placed in preventive quarantine. As a measure for the effectiveness of the policy, we defined the cost c by

where pq denotes the peak of the people in preventive quarantine and rc denotes the reduction of the peak of the confirmed cases. The higher this number, the more people have to be placed in preventive quarantine to achieve the same reduction of peak of the disease wave.
It can be seen that the location tracing based on shared workplaces achieves a peak reduction by about 30% regardless of the compliance level, whereas the household tracing performs better with an increasing compliance. Moreover, household tracing leads to a slight delay of the epidemic peak. For all three compliance levels, combined tracing for households and workplaces achieves the greatest peak reduction, performing better with a higher level of compliance.
3.4 Individual Tracing
The results of the individual tracing scenario, defined in Section 2.5.4 are shown in Figures 5, 6, and 7 and Table 2, respectively.
Simulation results for individual-tracing policies.
For all levels of compliance, individual tracing manages to further decrease the epidemic peak without increasing the peak of the people placed under preventive quarantine. Interestingly, the reduction of the epidemic peak achieved by a tracing rate of 75% does not vary much based on the compliance level. However, since the height of the epidemic peak decreases with an increasing compliance level, fewer people have to be placed under preventive quarantine to achieve this reduction. Thus, with an increasing level of compliance tracing becomes more effective.
4 Discussion
4.1 Evaluation of Tracing Policies
First of all, the model results indicate that tracing, in any characteristic, is a suitable policy to contain the disease and can supplement lockdown policies with high contact reduction. Yet, isolating persons due to a preventive quarantine measure is always related to economic and social problems – in particular, if the isolation turns out to be unnecessary. Consequently, any tracing measure should focus on keeping the total number of isolated persons as small as possible to reduce socioeconomic damage.
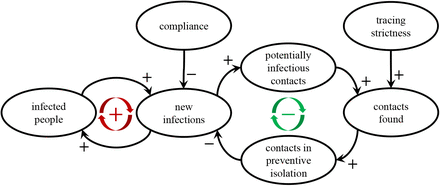
Hereby, highly interesting dynamics occur due to the interplay of two feedback loops which are depicted in Figure 8. As long as the feedback loop of the infectious and infected persons dominates the system, a lot of new infections will increase the number of persons in preventive isolation and therefore the economic costs. Increasing the strictness of the tracing measure, i.e. trace more rigorously, will contribute to make the right feedback loop dominant and contain the disease. Yet, it directly increases the number of quarantined people at first. Combined with compliance among the population, both, the infected and the preventive isolated people can be held on a low level.
Causal Loop Diagram of relevant system components with respect to tracing measures. The more dominant the feed-back loop on the left-hand side, the more potentially infectious contact partners need to be isolated to contain the disease.
The defined cost function c is used to quantify the efforts of a specific tracing strategy and relates with the direct benefit of the policy regarding the flattening of the curve. As a result of the high baseline runs, also the quarantine measures come at a comparably high price. Hereby, it directly correlates with the accuracy of the measure, i.e. the probability that a preventive isolated person is actually infected. Temporary closing of workplaces is clearly the least “precise” of the modelled policies as it affects the highest number of persons. Isolating household members is more “accurate”, but leaves many infections outside of households untraced. Our model suggests that the better the disease is contained, the higher the percentage of infections within households, and consequently, the more effective isolation of household members of infectious persons turns out to be.
Figure 9 shows a comparison between the height of the peak of the disease and the maximum number of agents in preventive isolation for all baselines and tracing policies. It reveals a highly interesting interplay between the number of isolated persons and the maximum peak height of the disease wave: On the one hand, a lower peak height implies stricter quarantine policies and more persons affected by them. On the other hand, a lower peak height leads to fewer persons requiring isolation. As the latter impact is nonlinear, the negative correlating impact dominates the positive one: if the disease is contained well, strict tracing policies are less costly than loose ones. For example, the number of preventive quarantined persons in the high compliance scenario increased to about 37% of the population with the combined tracing and decreased again to 28% with the 75% individual tracing although the policy is more restrictive. Compared to the low compliance scenario in which the corresponding numbers were 53% and 51% the same effect is visible, but less marked.
Impact of all location and individual tracing policies on both the epidemic peak and the number of persons isolated at home. Although tightening the policies leads to higher number of quarantined people at first, the number of isolated persons tends to decrease with the epidemic peak size if the policies are effective.
Clearly, the defined cost function can not remain the only one that should be considered in order to evaluate and compare measures. We must consider costs with respect to implementation and control of the policy and, in particular, heavy losses of personal freedom that can hardly be quantified at all. Unfortunately, the model indicates that the least efficient policies are the ones which could be implemented the easiest and vice versa.
In summary, the model indicates that all tracing measures contribute to reduction of the maximum peak-height. Hereby the effect of the policy can be set in relation with an alternative policy that focuses on reduction of leisure time contacts. As displayed in Table 2, the baseline peak of high compliance scenario is very similar as the combined location tracing peak of the low compliance scenario. Consequently, according to the definition of the baseline scenarios in Section 3.2, the model indicates that well performed location tracing could supplement a reduction of the number of leisure time contacts by 75%. Additional individual tracing would supplement for an even higher reduction. If only household or workplace tracing is applied, the benefits vary with the compliance – the higher the compliance, the more effective tracing of households becomes in comparison to workplace tracing.
In general, the findings of this work match the experience of countries that already implemented large-scale contact tracing like Singapore, provinces of China or South Korea [29,33,35]. Yet, in particular the chosen strategy in South Korea underlines, that pure contact tracing alone might not be sufficient to fully contain the disease. With respect to quantity, the reduction of the peak under tracing measures tops with 80% for the 75% individual tracing scenario, which matches with the highest estimate in [32] – in this summary of 29 COVID-19 studies (10 modelling studies) the reduction of incident cases under quarantine measures ranges from 44% to 81%.
4.2 Estimate of R0 and General Consequences for Disease Containment
Although not directly related with tracing, the calibration process revealed a modelled basic reproduction number R0 of COVID-19 in Austria of about 4.5, which is considerably high compared to most other estimates in literature. We assume that this is mainly due to two reasons: First of all, the number originates from the calibration data which is not cleaned with respect to a reporting bias. It is legitimate to assume that the slope of the actual curve at the beginning of the disease-wave is smaller than reported (see report for “nowcasting” attempts by the Robert Koch Institute(RKI, [21]) in Germany. Yet, the second, more important reason for our comparably high R0 is that typical estimates for this number, gained by fitting a Susceptible-Infectious-Recovered (SIR) or an exponential model, are usually lower than analogous R0 estimates based on fitting a Susceptible-Exposed-Infectious-Recovered (SEIR) model – or generally any model that includes a latency/incubation phase (see [26]).
Anyway, the modelled R0 indicates that the infection rate needs to be reduced below 1/R0 ≈ 22% of its original value in order to reach a fully contained behaviour of the disease, either by reduction of contacts and/or strict distancing and hygiene measures. As a matter of fact, this number is almost impossible to interpret in real life, mainly because there are lots of processes for which infectivity can hardly be reduced properly. The most important of these are definitely contacts within households which hardly be reduced by any measurement or policy.
Our model considers this problem and makes it possible to implement policies much more realistically: Considering that household contacts cannot be target of any policy, our model indicates that all other contacts would have to be reduced below approximately 12%, instead of 22%, of their original value to achieve full containment. Only considering policies for reduction of leisure time contacts, but not school or workplace contacts, this point cannot be reached at all. Consequently, it is not surprising that the chosen baseline scenarios do not lead to a properly contained disease in the model.
4.3 Model Features and Limitations
Due to the highly flexible policy timeline, the model is capable of testing and combining lots of different policies in different characteristics and at different times. Hence, it can easily depict almost any specified policy announced in reality, if estimates for the policy parameters are available.
The latter statement particularly refers to combination of policies: although the model correctly depicts the epidemiological impact of the combination of policies, the social impact needs to be parametrised manually. For instance, the causal relation between closed schools and intensified grandparents-children contacts needs to be parametrised and is not given by the model dynamics.
As the model cannot be scaled down, a huge number of agents leads to long computation times, and the necessity of Monte Carlo simulation for flattening of stochastic results increases the time required to get simulation output even more. As a consequence, the simulation’s capabilities of dealing with multi-variate calibration problems are limited and the model is unhandy to generate short-time prognoses.
Finally, the model disregards “death” as a final disease state as the model does not distinguish between deceased and recovered agents. Though this feature could easily be added to the model, we made this simplification as a conscious decision at the beginning of the modelling process. First, this feature is irrelevant for our modelling purpose and secondly, we did not intend to contribute to the rising panic among the population due to death-count prognoses.
5 Conclusion
We presented am agent-based simulation model that is capable of evaluating different tracing policies. By doing so we showed the limits of classical macroscopic cohort models, as comparable scenarios would not be feasible with aggregated modelling approaches: By aggregating individual contacts into global contact rates, individual contact-chains are lost and tracing cannot be modelled.
In the simulation case studies, we investigated three baseline scenarios for a second outbreak of COVID-19. The chosen scenarios allowed us to simulate and quantify the impact of different tracing policies and draw conclusions about tracing in general.
The results show that tracing of potentially infectious contacts and subsequent isolation of affected persons is a very useful measure to slow the spread of COVID-19 and that there are many different ways to do so. In particular, if the compliance for hygiene and contact reduction among the population is high, tracing policies are not only successful, but also cheap with respect to the number of isolated persons.
The features for evaluating the effectiveness of tracing policies is only one of many features of this advanced ABM. Although the model has limitations it is a well-founded basis for COVID-19 related decision support as it is capable of including complicated model-logic and diverse and high-resolution data.
Data Availability
All parametrisation data and links to data sources are found in Appendix and References.
6 Appendix
6.1 Model Details
Clearly, Section 2.1 could only outline the basic concepts of the model and left a lot of technical and modelling details open that are necessary for a reproducible model definition. In particular, this refers to the highly non-trivial initialisation process of the model. Hereby, two problems occur that require completely different approaches. The first problem considers the generation of the person-agents, locations and hospitals in the first place. The second problem deals with the initialisation of the status quo of the distribution of the disease states of the agents for the specified initial date.
6.1.1 Initialisation of Person-agents, Locations and Hospitals
A lot of problems that deal with the sampling of the initial population have already been solved in the original GEPOC model [13]. In particular this refers to the delaunay-triangulation-based sampling method for locations. We apply this method to merge information from the national statistics institute and the global human settlement layer [17]. Consequently, besides initialisation of the disease states which is described in the next section, only new methods for location- and hospital-generation had to be implemented.
Schools are initialised based on known distributions w.r.t. average school size and number of pupils in total. A school-sampler iteratively generates schools with a random size/capacity (truncated normal distribution) until the sum of all capacities matches the known number of pupils in reality. Each school is furthermore sampled a position (latitude and longitude) analogous to the sampling for person-locations (see [13]). In a second step, schools are “filled” with person agents. In this process, model agents with age between 6 and 18 are assigned to a school via a region-specific distribution analogous to the sampling of leisure-time contacts (see 2.1.4). Clearly, the number of model agents in this age group is larger than the number of known pupils. Consequently, we force distribution of all 6 to 14 year old agents, and distribute as many 15 to 18 year old agents as possible. All remaining 15 to 18 year old agents are considered to be working.
Workplaces2 are initialised analogously to schools. A workplace-sampler iteratively generates workplaces with size/capacity according to a discrete distribution (see Table 4). The sampler stops generating if the sum of all capacities matches (a + b)(1 − α), whereas a denotes all model agents between 19 and 64, b denotes all agents between 15 and 18 that have not yet been assigned a school, and α denotes the current unemployment rate. Location sampling and “filling” works analogously to the school-sampler.
Hospitals are generated based on publicly available data. This includes capacities (beds, intensive-care units) as well as their location (latitude and longitude).
6.1.2 Initialisation of the Disease State
The spread of SARS-CoV-2 displays probably better than any other system, that the most dangerous enemy is the invisible one. While confirmed infected persons are detected and well known, they hardly contribute to the spread of the disease – they are already isolated properly, and most infections occur even before the onset of symptoms.
Consequently, it is not possible to simply “start” the simulation with a certain number of confirmed cases, acquired for example from official internet sources. Valid values for pre-symptomatic (e.g. persons within latency and incubation period) and asymptomatic persons need to be acquired as well – yet, this number is hardly measurable in reality.
In order to solve this problem, a three stage concept, henceforth denoted as initialisation phase, was designed to generate a feasible initial state for a certain time t0:
Initialise-Simulation. The agent-based COVID-19 model is set up with a small number of initially infected agents. This number corresponds to an estimated count of initial infection clusters in the country, but actually hardly influences the outcome. Furthermore, the agent-based simulation is run and interrupted by a state event, namely if the cumulative number of confirmed agents in the model is greater or equal to a specific value C(t−1), where t−1 refers to a self chosen point in time and C(t−1) to the reported number of positive tests in reality until t−1. For this process, t−1 must be chosen properly so that the reported number of positive tests is large enough to be representative yet before implementation of any policies.
As soon as the simulation is interrupted by the state-event, the timelines of simulation and reality are synced: t−1 in reality becomes t−1 in the simulation.
The initialise-simulation is continued, considering all policies that have been implemented in reality, until, finally, t0 is reached. Properly calibrated by a calibration routine (see Section 6.1.4), the initialise-simulation contains approximately the same cumulative number of confirmed agents as the corresponding reported number in the real system.
The initialise-simulation is finished by exporting parts of the final state of the simulation. This refers to all households that contain either infected or recovered agents which are finally written into a file. With this strategy, an initial population is generated that contains not only a valid approximation of the confirmed cases, but also a valid estimate for the unknown pre-symptomatic and asymptomatic persons, a correct distribution of their future planned events and a correct household distribution as well.
Fine Tuning. Even with best calibration routines (see Section 6.1.4) it is not possible to perfectly match the model output with the status quo in reality, in particular w.r.t. regional distribution. Therefore, a bootstrapping algorithm was implemented that corrects the small differences between the initialise-simulation output and the real data (confirmed cases, hospitalisation, intensive-care units and recoveries per region) to make sure, that the initial state of the actual simulation matches the current state precisely. This step can be omitted, if matching the current state precisely is not required.
Load Households. Finally, the actual simulation is initialised with the previously recorded and fine-tuned agents from the initialise-simulation. To be precise, this process does not only include agents themselves, but also the households these agents live in. With this approach, at least, the fundamental network structure from the initialise-simulation can be maintained.
6.1.3 Parametrisation
We finally state a list of used parameters and parameter-values including corresponding sources and/or justifications. They are found in Tables 3, 4, and 6.
List of population specific parameters
6.1.4 Calibration
Clearly, there is no valid data available for direct parametrisation of the infection probability in case of a direct contact. First of all, this parameter is hardly measurable in reality and moreover strongly depends on the definition of “contact”. Consequently, this parameter needs to be fitted in the course of a calibration loop.
The calibration experiment is set up as follows:
We vary the parameter infection probability using a bisection algorithm.
For each parameter value, the simulation, parametrised without any policies, is executed ten times (Monte Carlo simulation) and the results are averaged.
The average time-series for the cumulative confirmed cases is observed and cropped to the beginning upswing of the epidemic curve, to be specific, all values between 200 and 3200. In this interval the growth of the curve can be considered as exponential.
The cropped time-series is compared with the corresponding time-series of real measured data in Austria, specifically the confirmed numbers between March 10th and 20th 2020 (source EMS system, [2]).
Both time-series are compared w.r.t. the average doubling time of the confirmed cases. The difference between the doubling times is taken as the calibration error for the bisection algorithm.
Note: As the sample standard deviation of each observable of the runs has been observed to be at most a fifth of the sample mean, the iteration number of nine for the Monte Carlo simulation has been considered to be sufficient for calibration purposes w.r.t. the ideas in [14,23].
6.2 Technical Implementation Details
The implementation of the agent-based COVID-19 model uses JAVA 11 and applies the UniformRandomProvider random number generator (RNG) by Apache Commons [1]. This RNG implements a 64 bit version of the Mersenne Twister [28] and exceeds the standard RNG of JAVA, a simple Linear Congruential Generator, in both performance and quality.
The simulation itself is always executed in a Monte Carlo setting and several runs with different RNG seeds are averaged. Due to the huge number of agents, a Law-of-Large-Numbers-effect can be observed (similar to [12] Chapter 5.2), and the standard deviation of the model output is always comparably small. Consequently, Monte Carlo replication numbers of 10 to 20 are usually enough to estimate the mean sufficiently well (we apply the algorithms from [14,23]).
6.3 Detailed Scenario Definition
In order to give a reproducible definition of scenarios, we explain the used policy-timelines in detail in tables 7 and 8. The prior shows the calibrated timeline of initialisation phase, the latter displays the timeline of the baseline scenarios.
List of contact specific parameters. Note that all parameter values are specified for the standard model without policies. The Γ-distribution is given as Γ(k, θ).
List of disease specific parameters (1/2).
List of disease specific parameters (2/2).
Model policies introduced to fit the current lockdown time-series in Austria
Baseline Scenarios high, medium and low compliance: Lift of the lockdown measures on May 1st 2020.
Footnotes
↵1 This number corresponds to the actual state of the confirmed cases on the specified date at the specified time. Due to a reporting bias, this number is subject to constant changes and will probably increase in the future.
↵2 Workplaces should not be confused with total companies. They rather represent the different teams where the members are in regular contact with each other.