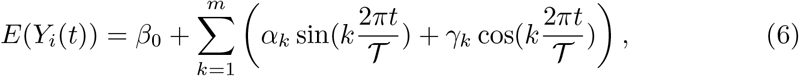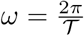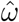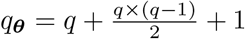Assessing COVID-19 pandemic excess deaths in Brazil: years 2020 and 2021

Saditt Rocio Robles Colonia, Lara Morena Cardeal, Rogério Antonio de Oliveirax, Luzia Aparecida Trinca
doi: https://doi.org/10.1101/2022.07.27.22278096

Abstract

We estimated the impact of the COVID-19 pandemic on mortality in Brazil for 2020 and 2021 years. We used mortality data (2015-2021) from the Health Ministry, Brazil government, to fit linear mixed models for forecasting baseline deaths under non-pandemic conditions. An advantage of the linear mixed model is the flexibility to capture year-trend while dealing with the correlations among death counts over time. Following a specified model building strategy, estimation of all-cause excess deaths at the country level and stratified by sex, age, ethnicity and region of residence, from March 2020 to August 2021. We also considered the estimation of excess deaths by specific causes. Estimated all-cause excess deaths was 199 108 (95% PI: 171 007; 227 209, P-Score=17.3%) for weeks 10-53, 2020, and 417 167 (95% PI: 372 075; 462 259, P-Score=50.1%) for weeks 1-32, 2021. P-scores ranged from 5.4% (RS, South) to 36.2% (AM, North) in 2020 and from 29.3% (AL, Northeast) to 94.9% (RO, North) in 2021. Differences among men (18.9%) and women (14.2%) appeared in 2020 only, and the P-scores were about 51% for both sexes in 2021. Except for youngsters (< 20 years old), all adult age groups were badly hit, especially those from 40 to 79 years old. In 2020, the Indigenous+East Asian population had the highest P-score (27%), and the Black population suffered the greatest impact (61.9%) in 2021. The pandemic impact had enormous regional heterogeneity and substantial differences according to socio-demographic factors, mainly during the first wave, showing some population strata benefits from the social distancing measures when able to adhere to them. In the second wave, the burden was very high for all but extremely high for some, highlighting our society needs to tackle the health inequalities experienced by groups of different socio-demographic and economic status.

Introduction

By the end of 2021, Brazil’s coronavirus disease (COVID-19) death toll was 619 334 (11.4% of the world), putting the country among the most affected, behind the USA only [1]. Accounting for the total impact of pandemics on mortality is relevant for a better understanding of its consequences while acknowledging deficiencies and hardships population groups are subjected to. This may be captured by estimating the excess deaths attributable to the pandemic, the difference between the observed and the predicted expectation or baseline deaths, over the same period, had the pandemic not happened [1–6]. Excess death measures are preferable to COVID-19 deaths because they account for direct and indirect effects of the pandemic and circumvent the issues related to limited testing and death-cause misreporting countries were subject to [7, 8]. Mortality might increase due to several other factors apart from COVID-19, e.g. disrupted health systems and treatment interruptions. In a countrywide survey, Horta et al. [9], found that about 25% of the interviewees reported failing to seek care due to a health problem or missed a routine examination during the first six months of the pandemic. Additionally, mitigation measures imposed to control transmission can impact mortality downwards by lowering the risk of accidents, homicides and exposure to other infectious diseases [3, 4, 10].

There are several methods of excess deaths estimation, from the simple previous years’ averaging to quite demanding models requiring census data [2, 3, 6]. Recently Barnard et al. [6] compared several models while Verbeeck et al. [3] pointed out, apart from other problems, the data violations on assumptions of some of the models frequently used. A common data violation is the implicit correlations of the historical mortality time series not incorporated in several models. Another point is that some methods fail to account for the specific-year mortality trend. Verbeeck et al. [3] acknowledged the issues with the usual approaches and showed that a linear mixed model, capable of capturing the mean and the variance-covariance patterns of historical mortality data, is well suited to forecast the year-specific baseline mortality for 2020. Employing the LMM model and the Brazilian mortality data (Health Ministry, Brazil Government), we estimate excess death due to the COVID-19 pandemic from March 2020 to early August 2021.

Pandemic excess death in Brazil’s mortality has been studied by several authors, using different data sources, locations and periods [4, 10–18]. Santos et al. [4] presented an account on excess deaths for the year 2020 by using the Negative Binomial regression model. Their modeling did not consider correlations between deaths counts time series and required population census data. Our paper aims to extend this work by using more up to date data and the flexible linear mixed model (LMM). A criticism of LMM is the underlying normality assumption but since weekly mortality assume large values, good approximation is attained [3, 10]. Advantages of the LMM are that it does not require information from the population beyond mortality and offers more conforming standard errors for the predictions since we can model the variability among years and the correlations between counts over time.

Brazil’s territory is organized into five major regions, each sub-divided into several federation units: 26 states and the Federal District, hereafter referred to as states for simplicity. Each state/municipality government was responsible for ruling the pandemic control measures. Although most states adopted some mitigation measures to control the virus spread [19], at least at some point, several factors contributed to the high Brazilian figure. The lack of unity of institutions in delivering the right messages to the population, difficulties for low-income people accessing social security and engaging in physical distancing and some delay in starting vaccination all seem to have contributed to the worse [10, 12, 20, 21]. Allied to that there is the huge regional diversity concerning health services, cultural and socio-demographic factors across the country. We investigate the regional patterns of excess all-cause deaths and patterns for demographic factors such as sex, age and race/skin color at the country level. For insights to understand excess and/or deficit we also predicted excess deaths due to other causes.

Materials and methods

Data

We obtained the publicly available data (2015-2021) from the Mortality Information System (SIM) [22], Ministry of Health, Brazil Government, on 7 March 2022. Each SIM record refers to an unidentified death, including death date, some socio-demographic factors and basic cause. We grouped deaths by epidemiological week (US CDC definition) at several levels of stratification: country, state, sex, age group, race/skin color and basic death cause. For death cause classification, we used the criteria of Santos et al. [4] and formed eight classes: COVID-19, Other Infectious Diseases, Neoplasms, Cardiovascular Diseases, Respiratory Diseases, Ill-Defined Causes, External Causes and Others.

For data preparation and handling, we acknowledge enormous benefit from the publicly available program code of Santos et al. [4].

The linear mixed model

The first documented COVID-19 death occurred on 12 March 2020, allowing a non-pandemic period of 9 weeks to estimate the 2020-specific trend. Thus, historical weekly mortality data from week 1, 2015 to week 9, 2020, was used to select the appropriate LMM for forecasting the all-cause deaths: a) at the country level, b) stratified by state, c) stratified by sex, d) stratified by age group and, e) stratified by race/skin color. In addition, deaths stratified by basic cause was modeled for accounting for the pandemic effects on other diseases.

In the mixed model framework, each year is considered a unit or cluster and weeks within a year are the observational units. A linear mixed model involves the modeling of three components: the mean or fixed-effects structure, the random-effects structure and the serial correlation structure. Using standard notation, let Yi denote the response vector (Ti × 1) for year i (i = 1, 2, …, M). Ti refers to the number of epidemiological weeks of year i and M = 6 is the number of years (2015-2020). For the period considered, all years have 52 weeks except 2020 that has 53 weeks. However, for the mixed model, 2020 data from weeks 10 to 53 are considered missing since this is the pandemic period and the mixed model will be used to predict baseline mortality under non pandemic circumstances. 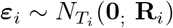The LMM is Embedded Image wherein Xi is the mean model matrix (Ti × p); β is the vector of fixed parameters (p × 1); Zi is the model matrix for the random terms (Ti × q); bi ∼ Nq(0; Di) is the year-specific random effects vector and Embedded Image is the random measurement errors vector. As standard, bi and εi are assumed independent. There are many choices for each part of the model. The columns of Xi could be indicators for weeks or could accommodate some function of weeks, as a quantitative explanatory variable, selected from a wide class of functions. The selected function should capture seasonal and trend effects. Other relevant covariates for explaining the mean of death counts could be included as well. The columns of Zi depend on the required random components to explain clustering and variability from year-to-year death patterns. The forms of the covariance matrices Di and Ri should account for the variances and correlation patterns of the random terms and depend on other parameters θi. Usually, it is assumed the random components share the same distribution among units, that is, θi = θ, Di = D and Ri = R for i = 1, 2, …, 6, but that is not a requirement. In that case, θ is a qθ × 1 vector. For the model under these assumptions and further independence among all random terms, that is, D and R = σ2I diagonal matrices, qθ = q + 1. The model in (1) implies that 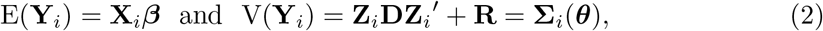Embedded Image the so called marginal model. Given the year-specific effects bi, we have the conditional model, 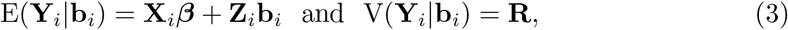Embedded Image responsible for predicting year-specific baseline mortality once the parameters are estimated.

Classical methods for estimation of the LMM parameters are Maximum Likelihood (ML) and Restricted Maximum Likelihood (REML) [23–25]. It is known that, given θ, the β ML estimator can be obtained from the generalized least squares formula (mixed model equations), 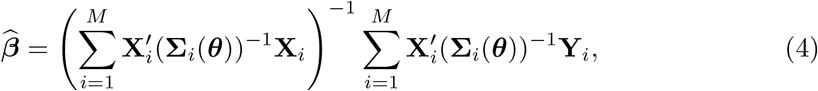Embedded Image which is the best linear unbiased estimator (BLUE) for β. Predictions for the random effects are also derived 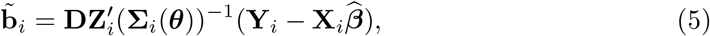Embedded Image resulting in the best linear unbiased predictor (BLUP) for bi.

For unknown θ, both parameter vectors can be estimated by ML using some iterative procedure, however, rendering biased estimates for θ. REML, proposed by [23], is preferable since it accounts for the degrees of freedom loss in the process of β estimation and is expected to yield less biased estimators for θ. Substituting 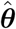Embedded Image in Eqs (4) and (5) results in the so called empirical BLUE and empirical BLUP, respectively.

Likelihood ratio type tests, information criteria, residuals and other measures for model fitting diagnostic analysis such as those proposed in [26] are all useful to model selection. Extra care should be thought since changes in one component can affect the other, and it is not clear which strategy is the best. It is usually agreed that one should search for a good representation of the mean and proceed by adding random effects as necessary to account for clustering and specific effects for units. And, for last, proceed to account for serial correlations as required. With this general strategy in mind, and considering week effects in the fixed part, we outline the steps proposed to select a parsimonious model to predict the baseline number of deaths.

Modeling strategy

  1. Fit of a linear fixed effects model considering the years as a blocking factor and the weeks as a qualitative factor. This will be referred as Model 0.

  2. Search for functions of time that adequately capture the yearly cyclic pattern. Functions based on Fourier series (FS), as suggested by [3], showed to be adequate, except for modeling External Causes mortality that required a conventional quadratic model. The FS for the mean (marginal) model is Embedded Image wherein Yi(t) is the number of death at time t, in year i, 𝒯 is the series period and m is the number of terms required in the FS. To select the period 𝒯 (or equivalently the frequency Embedded Image) the approach indicated in [24] was used, that is, we fitted a non-linear model to estimate the ω parameter. In the case of our data, we fitted a non-linear model with years as a blocking factor and m = 2. This is convenient since the model captures the year effect but remains partially linear, requiring an initial value for ω only. Once Embedded Image is obtained, the regression linear model can be fitted and tested for lack-of-fit against Model 0 and some basic residual analysis performed. Under evidence of lack-of-fit of the model, we can search for a more complex function of time, increasing the number of terms in the FS, for example. Some degree of lack of fit might be tolerated (but this was not the case in our applications) since it can be captured in the mixed model in the next steps as the mixed model allows the inclusion of the random part for the regression parameters. That would take into account the possible interactions between years and weeks, for example. The final model in this step will be referred as Model 1.

  3. Fit, by REML, a linear mixed model with the mean part found in step 2 including full random effects, one for accounting for years variability and one associated to each element of β, assuming unstructured D. This will be called Model 2, with the number of parameters in θ given by Embedded Image.

  4. Try simplification of the structure of D by declaring D diagonal. Explore other models, possibly dropping some random effects based on the magnitude of variance component estimates and their standard errors or performing some formal tests. The simpler model not showing lack-of-fit, when compared to the more complex one, is kept. This will be Model 3.

  5. Update Model 3 by incorporating some structure in the matrix R. Some usual possibilities are first-order auto-regressive (AR(1)), Gaussian and Spherical correlation patterns [24]. These models can be compared by AIC and/or BIC values. In the case of AR(1), it is nested in Model 3 and the likelihood ratio test is applicable. Select the more parsimonious model and call it Model 4.

  6. Check for further simplification of the random part as some random effects in bI might not be relevant. Keep the more parsimonious model (Model 5).

  7. Refit Model 5 by ML (call it Model 6) and check for simplification of the mean model by dropping some terms of the FS. Keep the more parsimonious model (Model 7).

  8. Refit Model 7 by REML (call Model 8) and perform detailed diagnostic analysis of the fit. In case of evidence of violations, some fix may be possible by following recommendations in [26].

To compare nested mixed models in the random structure with the same fixed terms, we used the likelihood ratio test, based on the REML method. In the case of hypothesis for variances, the p-values were corrected by the chi-bar-square distribution [27]. To compare nested models in the fixed part with the same random structure, we used the likelihood ratio test based on the ML method. Once simplified, the final model was refitted by REML as indicated in step 8.

Prediction Accuracy

To assess the prediction accuracy of the LMM we used the square root of forecast error (RMSE) and the mean absolute percentage error (MAPE). For this task, we used data from 2010-2019 such that for each year i in turn, from 2015 to 2019 (i = 1, 2, …, 5), we fitted each model being compared using data from the previous five-year history and the 9 first weeks of year i. 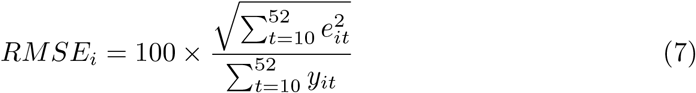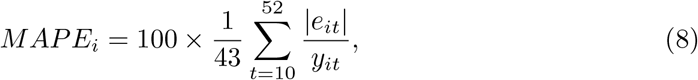Then, for year i, we obtained forecasts for t = 10, 11, …, 52 and evaluated: Embedded Image and Embedded Image wherein eit is the difference between the observed and the forecast in week t (t = 10, 2, …, 52), for each year in turn (i = 1, 2, …, 5).

Baseline death prediction intervals

The 2020-specific conditional empirical best linear unbiased predictor from the final model was used as the 2020 baseline mortality. Let 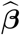Embedded Image be the empirical BLUE of β and 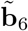Embedded Image be the empirical BLUP of b6 (i = 6 refers to 2020). It is instructive to write the 2020 prediction vector in two parts, one for weeks 1-9 (pre-pandemic, data is available and used to fit the model), given by 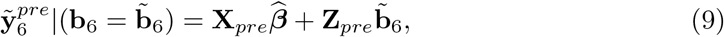Embedded Image wherein pre stands for the part of the matrices referring to the pre-pandemic period. For weeks 10-53 (pandemic period, no data are available) the predictions are 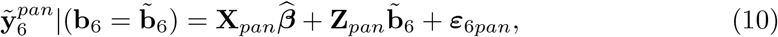Embedded Image wherein pan refers to the pandemic period. For obtaining 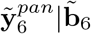Embedded Image in (10) we substitute ε6pan by its best predictor available, i.e the null vector, and the distinction between predictions formulae (9) and (10) is with respect to their variances. 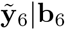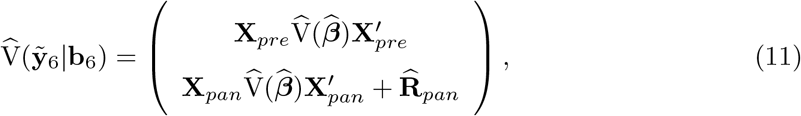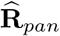The variance-covariance matrix of the complete predicted vector Embedded Image is Embedded Image wherein Embedded Image is the block of the matrix 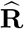Embedded Image with respect to weeks 10-53 and 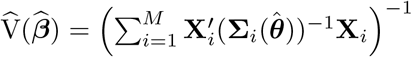Embedded Image is the first-order approximation estimator of the variance-covariance of 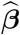Embedded Image. Note that for the pandemic period, we want to forecast non-observable mortality and variability due to the random measurement error should be taken into account. The fitted model offers a forecast for week 53 since this time point is close to the upper limit of the time range of the data used for the baseline modeling, e. g. extrapolation error is not a big issue here. We need to accommodate 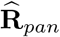Embedded Image as well for week 53. Under the homogeneous errors assumption, which we will see the data show no violation, this is easy do deal with.

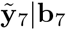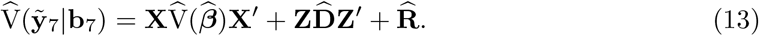For the year 2021 (i = 7), no non-pandemic data is observable and there is no prediction of the year-specific effect. Thus, Embedded Image is Embedded Image and the best predictors for both, b7 and ε7, are zero, from the assumed model. Then, the variance-covariance is Embedded Image For prediction intervals (PI), standard errors 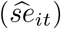Embedded Image are estimated by the squared root of the diagonal elements of (11) and (13). 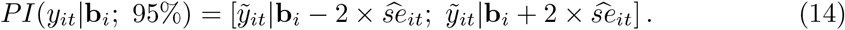Approximate 95% PI’s are calculated using the standard method (Normal approximation): Embedded Image

Excess deaths

Excess deaths in week t for years 2020 and 2021 (i = 6, 7) are estimated as the observed number of deaths (yit) minus the predicted baseline deaths: Embedded Image These were obtained for all-cause deaths as well as for the cause-specific models, both stratified by the factors described earlier.

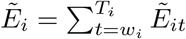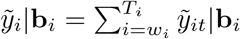For year summaries and fairer comparisons between strata we used the per capita of excess deaths denoted P-score [28], and the ratio excess by COVID-19 deaths, denoted RatioEC [4]. The year-accumulated P-score is defined as Embedded Image wherein Embedded Image and Embedded Image are, respectively, the annual predicted excess and the baseline deaths in year i (wi = 10 for year 2020 and wi = 1 for year 2021).

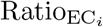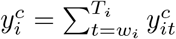The year-accumulated Embedded Image is Embedded Image wherein Embedded Image is the annual observed COVID-19 confirmed deaths. The 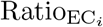Embedded Image is a measure of the COVID-19 pandemic effect on deaths attributable to other causes. Values below one mean that COVID-19 surpassed excess deaths such that there was a deficit in reporting deaths due to other causes, while values above one mean extra deaths due to other causes beyond COVID-19 amounted.

Computational resources

We used R [29] for all computations and package nlme [30] for fitting the linear mixed models. We compared nested models in the random parts using likelihood ratio tests based on REML with the p-values corrected by the chi-bar-square distribution, varTestnlme package [31], respectively. For the fitting diagnosis we used the R function lmmdiagnostic freely available for download at http://www.ime.usp.br/~jmsinger/lmmdiagnostics.zip.

Results

Excess deaths at the country level

Table 1 shows the fit information for modeling the all-cause weekly deaths in the whole country. To start with, two terms of the Fourier series (Model 1) with the estimated frequency 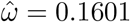Embedded Image, resulting in a period of approximately 39 weeks, showed a good approximation for the fixed part (p-value= 0.661 for the comparison of this simpler model to the full Model 0). The first mixed model fitted (Model 2) included five fixed parameters (the intercept plus four slopes for two waves of the Fourier series) and five random components, with unstructured D and diagonal R = σ2I (no serial correlations and homogeneous errors), such that qθ = 5 + 10 + 1 = 16. 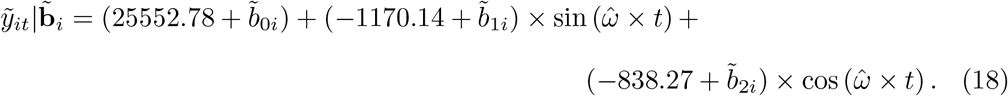Application of the selection strategy previously outlined resulted in the following final fitted baseline model: Embedded Image

View this table:
Table 1. Baseline model fitting information for all-cause weekly deaths based on historical data from week 1, 2015 to week 9, 2020.

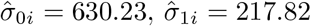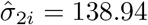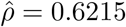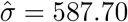The best selected structure for D was diagonal with variance component estimates given by Embedded Image and Embedded Image. The best structure for R was found to be the AR(1), with Embedded Image and Embedded Image. Table 1 shows the sequence of steps to the final model and the prediction accuracy measures summarized by the range of values obtained for five years. For comparison, the last row of the table shows the accuracy measure values using the historical five-year weekly average as the forecasts. The values were calculated for each year from 2015 to 2019, always using the previous five-year mortality data. The final and more parsimonious mixed model shows very good performances, with very slight differences in comparison to more complex models and much better than the five-year average approach (RMSE ranged from 0.4% to 0.7% and from 0.7% to 1.3% for our model and the average method, respectively; MAPE ranged from 2.0% to 3.9% and from 4.4% to 7.3% for our model and the average method, respectively). Diagnostics graphs did not reveal any concern about violations of the fitted model (see S1 Fig), reassuring the usefulness of the LMM approach for weekly mortality using historical data.

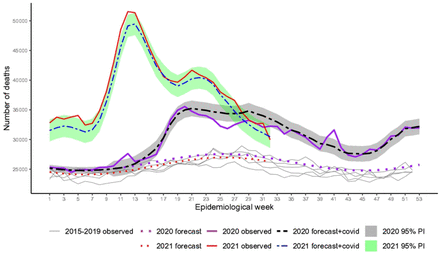
Fig 1 shows the observed weekly all-cause mortality for week 1, 2015 to week 32, 2021, the baseline forecasts for both years, and the 95% PI for expected mortality plus reported COVID-19 deaths (forecast + COVID-19). Excess occurred over the whole period since the surge of the first wave, 2020 and reached alarming figures in the second wave in 2021. In the beginning, excesses indicate more deaths occurred beyond COVID-19. From week 13 to around week 24, 2020 (last week of June), excesses agree well with COVID-19 as the main cause. From week 24 to, approximately, week 32, 2020, (beginning of August), COVID-19 exceeded deaths from all causes, i.e, deaths due to other causes were smaller than expected. A peak of excess deaths occurred again in week 41 (around 10 October). From week 44 to the end of the year, deaths increased with the second wave, and numbers agree well with COVID-19 deaths. In 2021, the spread of variant Gamma before vaccination began, associated with relaxation of social distancing, had a huge impact. Only by mid of July 2021, death numbers lowered down to the level of the worst period of the previous year. For occasion of the peak, around weeks 12-13 (end of March) only 2% of the country population was fully vaccinated. Vaccination for classified as high-risk groups, e.g. elderly and health workers, started very slowly in 18 January 2021 [32, 33].

Fig 1.
Fig 1. Weekly all-cause mortality in Brazil from week 1, 2015 to week 32, 2021.

Recorded and baseline mortality forecast by the LMM and the forecast plus observed COVID-19 deaths including 95% prediction intervals (PI) for 2020 and 2021.

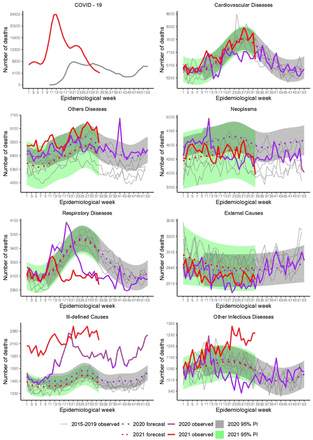
Table 2 includes summaries of expected and excess/deficit deaths accumulated according to specific causes and Fig 2 shows that excesses and deficits occurred for most causes, at different points in time, except for Ill-defined Causes showing substantial deaths since the pandemic started, totaling 18 596 (27.8%) and 24 923 (54.3%) excesses in 2020 and 2021, respectively (Table 2). For Respiratory, excesses occurred essentially at the beginning of the pandemic up to around week 21 (end of May 2020). After that, the impact was negative, with deficits until week 41 (early October). Overall the impact was negative with a deficit of −9 195 (−6.7%). In 2021, deaths had a quick increase by week 12 (end of March), but after that, mortality was smaller than expected during the rest of the period, resulting in a deficit of −12 192 (−12.2%). Mortality under Other Infectious Diseases showed a somewhat similar pattern to Respiratory in the year 2020, although on a smaller scale, with deficit deaths occurring during the weeks in the middle of the year (−2.9). However, in 2021, expressive mortality occurred, resembling the pattern of Ill-defined Causes (9.9%).

View this table:
Table 2. Reported, expected and estimated excess/deficit deaths by basic selected cause, accumulated for two periods, weeks 10-53, 2020 and weeks 1-32, 2021.
Fig 2.
Fig 2. Weekly mortality in Brazil, stratified by death cause, from week 1, 2015 to week 32, 2021.

Recorded and baseline mortality forecast by the LMM including 95% prediction intervals (PI) for 2020 and 2021.

Deficit deaths due to Neoplasms (−5.3%) and Cardiovascular Diseases (−2.4%) occurred from March to August in 2020, the period of tighter control measures, although a peak stands out for Neoplasms in the very beginning of the pandemic. For 2021, mortality followed the expected pattern closely.

Overall, External Causes did not suffer noteworthy impact as it would be expected due to the reduction of traffic and outdoor movements during restrictions, perhaps by the fact that many people were unable to comply to the rules.

From these inspections, we note that the first peak of excess deaths (week 12) in Fig 1 is related mainly to Ill-defined Causes, Neoplasms, Respiratory and Other Infectious Diseases. The peak in week 41, 2020, is related to these causes, except for Neoplasms. Accumulated deaths by each year showed 211 531 COVID-19 and 199 108 estimated excess deaths (95% PI: 171 007 to 227 209; RatioEC = 0.94) for weeks 10-53, 2020, and 380 180 COVID-19 and 417 167 estimated excess deaths (95% PI: 372 075 to 462 259; RatioEC = 1.10) for weeks 1-32, 2021 (Table 2). The P-Score estimates pointed out 17.3% and 50.1% more deaths than expected in 2020 and 2021, respectively.

Excess deaths by state

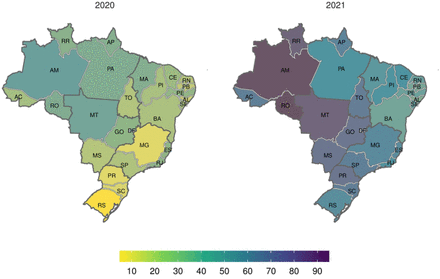
Excess deaths occurred in all states but with enormous heterogeneity across the country (S1 Tab). P-Scores ranged from 5.4% (RS, South) to 36.2% (AM, North) in 2020 and from 29.3% (AL, Northeast) to 94.9% (RO, North) in 2021 (Fig 3). The North and Central-West presented the enormous percentages in both years with RO and AM suffering alarming mortality per capita (> 90%) in 2021 while the South and part of Southeast showed smaller percentages in 2020, joined by the Northeast in 2021 although, as the map shows, P-scores were above 40% in almost the whole country in 2021.

Fig 3.
Fig 3. Regional variation with respect to cumulative P-Score (excess relative to expected deaths in %).

Weeks 10-53, 2020 and weeks 1-32, 2021.

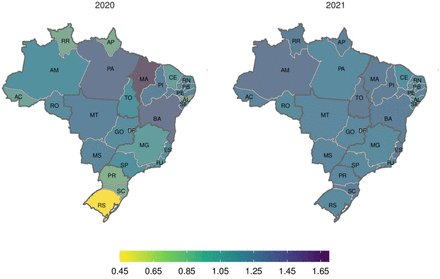
Fig 4 shows the regional heterogeneity concerning the excess and COVID-19 deaths ratio (RatioEC) accumulated at each year. In 2020 several states suffered at least 10% more excess deaths than COVID-19 (MA, BA, PI and PE in the Northeast, MT, MS and DF, in the Central-West and PA the North). A few others showed deficit deaths, with RS (South) presenting the minimum ratio (0.46). However, for the second wave, in 2021, the impact across the country was tantamount. Only one state (SE, in the Northeast) showed a ratio of 0.94. All other states showed a ratio very close to one or greater, with BA, MA, PI (Northeast), ES (Southeast), AM and TO (North) showing over 20% of excess surpassing COVID-19 deaths.

Fig 4.
Fig 4. Regional variation with respect to cumulative RatioEC (excess relative to COVID-19 deaths).

Weeks 10-53, 2020 and weeks 1-32, 2021.

Detailed results along time, shown in S2 Fig to S6 Fig, inform that, in general, the states that coped better with the pandemic in the first year (as pointed out above) showed deficit deaths during the first wave, suggesting that their population afforded better care for other diseases and, perhaps, afforded better compliance to isolation recommendations. However, cause-diagnostic mistakes and COVID-19 under-reporting, mainly in remote states, could also contribute to the figures.

In 2021, deficit deaths are not apparent in any of the states as the pandemic hit so badly the whole country and it was much more difficult for the population to practice isolation. Still, some states showed notable positive discrepancies between forecast+COVID-19 deaths and reported deaths again, mainly in the North, Northeast and Central-West regions.

Excess deaths according to sex, race/skin color and age

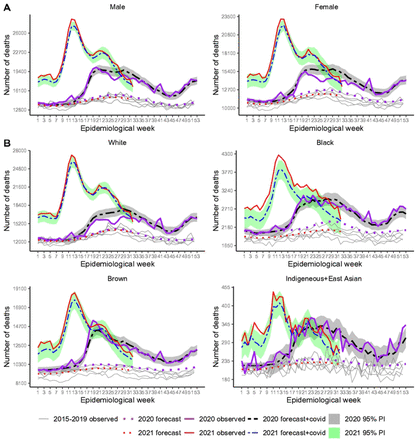
With respect to sex, Fig 5 (A) and Table 3 show that for female, excess (14.2%) was smaller than for male (18.9%). Nonetheless COVID-19 surpassed excess during several weeks in the middle of 2020 (RatioEC = 0.81) for female, while for male, differences were smaller and for shorter period resulting in RatioEC = 1.00. However, sex differences disappeared in 2021 with ratios of 1.10 and 1.09 and P-Score of 51.3% and 50.4% for female and male, respectively.

Fig 5.
Fig 5. Weekly mortality in Brazil, stratified by sex (A) and race/skin-color (B), from week 1, 2015 to week 32, 2021.

Recorded and baseline mortality forecast by the LMM including 95% prediction intervals (PI) for 2020 and 2021.

View this table:
Table 3. Reported, expected and estimated excess/deficit totals deaths and deaths by sex, race/skin color and age group, accumulated for two periods, weeks 10-53, 2020 and weeks 1-32, 2021.

Regarding race/skin color (Fig 5 (B)), the most striking result is the larger observed than predicted (forecast+COVID-19) deaths among blacks, mainly in 2021, an indication that excess surpassed COVID-19 deaths. The RatioEC ranged from 0.82 (White) to 1.13 (Others) in 2020, and from 1.06 (White) to 1.36 (Black) in 2021. The P-Score varied from 14.7% (White) to 27.0% (Others) and from 47.4% (Brown) to 61.9% (Black), in 2020 and 2021, respectively, showing how severely the black population was hit from both viewpoints, higher per capita mortality and excess deaths due to other causes beyond COVID-19.

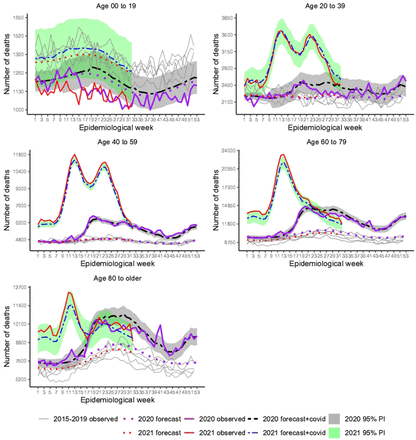
Fig 6 shows results stratified by age group. Deficit death prevailed in the group younger than 20 years old in 2020 (−5.7%) and 2021 (−17.0%). There is also some slight indication of deficit deaths, during the first wave, for the group 20-39 years old, but that disappeared from week 36, showing some peaks matching the loosening of isolation measures and the end of the year. The pattern for older groups is somewhat qualitatively similar to that shown in Fig 1. The decline after week 14, 2021, for the group aged 60 to 79 years old, may be related to better immunity as vaccination was advancing. It is also worth noting that, for 80 years old or more, mortality decreased with vaccination but soon increased again and kept at ≈ 10 000 fatalities per week after week 16, 2021. As summarized in Table 3, except for the already mentioned younger group, there were excess deaths in all age groups, with P-Score ranging from 6.4% (20-39 years old) to 22.2% (60-79 years old) and from 32.8% (20-29 years old) to 81.3% (40-59 years old) in 2020 and 2021, respectively.

Fig 6.
Fig 6. Weekly mortality in Brazil, stratified by age group, from week 1, 2015 to week 32, 2021.

Recorded and baseline mortality forecast by the LMM including 95% prediction intervals (PI) for 2020 and 2021.

Discussion

Since the COVID-19 pandemic declaration, in March 2020, excess deaths in Brazil amounted to 17.3% and 50.1% more than expected in 2020 and 2021, respectively. For 2020, our results, using LMM, unfold similar patterns published by Santos et al. [4], although estimates varies because the different modeling approaches and slight changes in the data set due updating. As also reported in other studies [4, 8, 18], our investigation highlights the enormous heterogeneity across Brazil, showing the South was less impacted (5.4%, in RS, to 11.7%, in SC), while the North and Central-West had the highest scores (∼ 30%) in terms of excess deaths in 2020. In 2021, however, P-scores ranged from 29.3% to 94.9%, with even RS (South) showing 47.5% more deaths. The state of RO presented the greatest P-score, followed by AM, both belonging to the North region. While several factors resulting in societal inequalities are likely to contribute to regional differences, for Brazil, we should add the failing of the country in delivering, as a whole, the awareness of the disease severity and the relevance of non-pharmacological measures [8, 21, 34].

Mortality profiles along time showed excess deaths smaller than reported COVID-19, indicating deficits due to other causes in 2020 only. Deficit deaths were noted mainly in the South and Southeast, where the population is usually better served in terms of healthcare and more advantaged economically which possibly contributed to better engagement in social distancing during the first wave. Cause-specific expected mortality indicated deficits for Respiratory, Other Infectious Diseases, Neoplasms and Cardiovascular Diseases. With the social distancing recommendations, we expect lower exposure to risk factors associated with the first two, while deficits for Neoplasms and Cardiovascular diseases might be explained by the evidence that people suffering from these illnesses were at high risk for serious COVID-19 conditions and died from COVID-19 in the first wave [14, 35–37]. While these arguments are plausible, we should keep in mind that misdiagnosis is always an issue mainly to deaths that happened outside hospitals and clinics and in regions with poor resources for proper diagnosis [13]. Of these diseases, only Respiratory maintained the deficit pattern in part of 2021, after week 22.

Excesses deaths beyond COVID-19 were typical at the beginning of the pandemic, about the end of the first wave, and all over 2021, from week 1 to week 32, (the period considered in our analysis), a signal of possible death cause misreporting [4, 8, 38, 39]. Temporal and regional differences were also present. In both years, excess deaths predominate for Ill-defined Causes with Other Infectious Diseases added in 2021. In most states from the North and Northeast regions, the excess beyond COVID-19 is noteworthy, raising, again, the debate of misdiagnosis and the lack of resources in an already impaired health infrastructure further aggravated by the pandemic [7].

Studies around the world [4, 5, 14, 40, 41 ] reported COVID-19 mortality affects more males than females, although some authors did not find relevant differences once baseline is considered [42]. Our results for 2020, based on excess deaths, are somewhat in line with [4], with 18.9% against 14.2% more extra deaths in males and females, respectively. However, for 2021, 51% more deaths were estimated for both sexes. Our analysis pointed out more prominent female deficit deaths only during the plateau of the first wave, an indication that in 2020, women might have been able to engage better in social distancing and avoided contamination by other infections. That could be a consequence of the well-known vulnerable forms of employment (informal self-employing, housework and children care responsibilities) females share, mainly in South American countries [40].

The pandemic impacted age groups differently as expected and shown in other studies [4, 5, 41, 43] with larger impact for people aged between 40 to 79 years old, in both years. The group younger than 20 showed deficit deaths in both years while for the elderly, COVID-19 surpassed excess deaths in the first year.

Excess exceeded deaths from COVID-19 in all race/skin color groups, except White, who had a deficit of deaths during part of the first wave and, once again, the relationship between race/skin color, socio-economic status and heath in Brazil is evident. By 2021, all groups were largely affected. However, the non-white population experienced an extra burden, either showing expected deaths from diseases other than COVID-19 or more likely to experience death-cause misdiagnosis. This is not surprising, unfortunately, as well exposed by several studies [44–47].

Data Availability

Data are available from Ministério da Saúde, Governo do Brasil: https://opendatasus.saude.gov.br/dataset/sim-1979-2019 https://opendatasus.saude.gov.br/dataset/sim-2020-2021 However data from 2021 is considered preliminary and might be moved to another url once consolidated.

Supporting information

S1 Fig. Diagnostic graph analysis for assumptions of the fitted LMM for all-cause deaths in Brazil (Eq 18). Standardized marginal residuals against marginal fitted response, standardized conditional residuals against predicted response, Normal probability plot for standardized least confounded conditional residual, Chi-square probability plot for Mahalanobis distance and Modified Lesaffre-Verbeck measure index plot.

S1 Tab. Reported, expected and estimated excess/deficit totals deaths by state, accumulated for two periods, weeks 10-53, 2020 and weeks 1-32, 2021

S2 Fig. Weekly all-cause mortality in the North Region states, Brazil, from week 1, 2015 to week 32, 2021. Recorded and baseline mortality forecast by the LMM and the forecast plus observed COVID-19 deaths including 95% prediction intervals for 2020 and 2021 (shaded areas).

S3 Fig. Weekly all-cause mortality in the Northeast Region states, Brazil, from week 1, 2015 to week 32, 2021. Recorded and baseline mortality forecast by the LMM and the forecast plus observed COVID-19 deaths including 95% prediction intervals for 2020 and 2021 (shaded areas).

S4 Fig. Weekly all-cause mortality in the Southeast Region states, Brazil, from week 1, 2015 to week 32, 2021. Recorded and baseline mortality forecast by the linear mixed model and the forecast plus observed COVID-19 deaths including 95% prediction intervals for 2020 and 2021.

S5 Fig. Weekly all-cause mortality in the South Region states, Brazil, from week 1, 2015 to week 32, 2021. Recorded and baseline mortality forecast by the linear mixed model and the forecast plus observed COVID-19 deaths including 95% prediction intervals for 2020 and 2021.

S6 Fig. Weekly all-cause mortality in the Central-West Region states, Brazil, from week 1, 2015 to week 32, 2021. Recorded and baseline mortality forecast by the linear mixed model and the forecast plus observed COVID-19 deaths including 95% prediction intervals for 2020 and 2021.

Acknowledgments

The first and second authors acknowledge research scholarships from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001.

References

  1. 1.↵
    Ritchie H, Mathieu E, Rodés-Guirao L, Appel C, Giattino C, Ortiz-Ospina E, et al. Coronavirus pandemic (COVID-19); 2020. https://ourworldindata.org/coronavirus.
  2. 2.↵
    Helleringer S, Queiroz BL. Commentary: Measuring excess mortality due to the COVID-19 pandemic: progress and persistent challenges. Int J Epidemiol. 2022;51:85–87. doi:10.1093/ije/dyab260.
    OpenUrlCrossRef
  3. 3.↵
    Verbeeck J, Faes C, Neyens T, Hens N, Verbeke G, Deboosere P, et al. A linear mixed model to estimate COVID-19-induced excess mortality. Biometrics. 2021;00:00–00. doi:10.1111/biom.13578.
    OpenUrlCrossRef
  4. 4.↵
    Santos AM, Souza BF, Carvalho CA, Campos MAG, Oliveira BLCA, Diniz EM, et al. Excess deaths from all causes and by COVID-19 in Brazil in 2020. Rev Saúde Públ. 2021;55:1–12. doi:10.11606/s1518-8787.2021055004137.
    OpenUrlCrossRef
  5. 5.↵
    Cúellar L, Torres I, Romero-Severson E, Mahesh R, Ortega N, Pungitore S, et al. Excess deaths reveal the true spatial, temporal and demographic impact of COVID-19 on mortality in Ecuador. Int J Epidemiol. 2022;52:54–62. doi:10.1093/ije/dyab163.
    OpenUrlCrossRef
  6. 6.↵
    Barnard S, Chiavenna C, Fox S, Charlett A, Waller Z, Andrews N, et al. Methods for modelling excess mortality across England during the COVID-19 pandemic. Stat Methods Med Res. 2021; p. 1–13. doi:10.1177/09622802211046384.
    OpenUrlCrossRef
  7. 7.↵
    Orellana JDY, da Cunha GM, Marrero L, Moreira RI, da Costa Leite I, Horta BL. Excesso de mortes durante a pandemia de COVID-19: subnotificação e desigualdades regionais no Brasil. Cad Saúde Pública. 2021;doi:10.1590/0102-311X00259120.
    OpenUrlCrossRef
  8. 8.↵
    Carvalho TA, Boschiero MN, Marson FAL. COVID-19 in Brazil: 150,000 deaths and the Brazilian underreporting. Diagn Microbiol Infect Dis. 2021;99:115258. doi:10.1016/j.diagmicrobio.2020.115258.
    OpenUrlCrossRef
  9. 9.↵
    Horta BL, Silveira MF, Barros AJD, Hartwig FP, Dias MS, Menezes AMB, et al. COVID-19 and outpatient care: a nationwide household survey. Cad de Saúde Pública. 2022;38:e00194121. doi:10.1590/0102-311x00194121.
    OpenUrlCrossRef
  10. 10.↵
    Borrego-Morell JA, Huertas EJ, Torrado N. On the effect of COVID-19 pandemic in the excess of human mortality. The case of Brazil and Spain. PLoS ONE. 2021;16:1–14. doi:10.1371/journal.pone.0255909.
    OpenUrlCrossRefPubMed
  11. 11.
    Alves THE, Souza TA, Silva SA, Ramos NA, Oliveira SV. Underreporting of death by COVID-19 in Brazil’s second most populous state. Frontiers in Public Health. 2020;8:1–7. doi:10.3389/fpubh.2020.578645.
    OpenUrlCrossRef
  12. 12.↵
    Azevedo e Silva G, Jardim BC, Santos CVB. Excesso de mortalidade no Brasil em tempos de COVID-19. Ciênc Saúde Colet. 2020;25:3345–3354.
    OpenUrl
  13. 13.↵
    Brant LCC, Nascimento BR, Teixeira RA, Lopes MACQ, Malta DC, Oliveira GMM, et al. Excess of cardiovascular deaths during the COVID-19 pandemic in Brazilian capital cities. Heart. 2020;106:1898–1905. doi:10.1136/heartjnl-2020-317663.
    OpenUrlAbstract/FREE Full Text
  14. 14.↵
    Fernandes GA, Junior APN, Azevedo e Silva G, Feriani D, França e Silva ILA, Caruso P, et al. Excess mortality by specific causes of deaths in the city of São Paulo, Brazil, during the COVID-19 pandemic. PLoS ONE. 2021;16:e0252238. doi:10.1371/journal.pone.0252238.
    OpenUrlCrossRef
  15. 15.
    Freitas ARR, Medeiros NM, Frutuoso LCV, Beckedorff OA, Martin LMA, Coelho MMM, et al. Tracking excess deaths associated with the COVID-19 epidemic as an epidemiological surveillance strategy-preliminary results of the evaluation of six Brazilian capitals. Rev Soc Bras Med Trop. 2020;53:e20200558. doi:10.1590/0037-8682-0558-2020.
    OpenUrlCrossRef
  16. 16.
    Marinho MF, Torrens A, Teixeira R, Brant LCC, Malta DC, Nascimento BR, et al. Racial disparity in excess mortality in Brazil during COVID-19 times. Eur J Public Health. 2022;32:24–26. doi:10.1093/eurpub/ckab097.
    OpenUrlCrossRef
  17. 17.
    Gimenez Junior GAA, Zilli PK, Silva LFF, Pasqualucci CA, Campo AB, Suemoto CK. Death trends based on autopsy data compared to the beginning of the coronavirus pandemic in Brazil. Braz J Med Biol Res. 2021;54:1–7. doi:10.1590/1414-431X202010766.
    OpenUrlCrossRef
  18. 18.↵
    Orellana JDY, Cunha GM, Marrero L, Moreira RI, da Costa Leite I, Horta BL. Excess deaths during the COVID-19 pandemic: underreporting and regional inequalities in Brazil. Cad Saúde Pública. 2021;37:1–16. doi:10.1590/0102-311X00259120.
    OpenUrlCrossRef
  19. 19.↵
    da Silva LLS, Lima AFR, Polli DA, Razia PFS, Pavão LFA, Cavalcanti MAFDH, et al. Social distancing measures in the fight against COVID-19 in Brazil: Description and epidemiological analysis by state. Cad Saúde Pública. 2020;36:e00185020. doi:10.1590/0102-311X00185020.
    OpenUrlCrossRef
  20. 20.↵
    Barberia LG, Gómez EJ. Political and institutional perils of Brazil’s COVID-19 crisis. Lancet. 2020;396:367–368. doi:10.1016/S0140-6736(20)31681-0.
    OpenUrlCrossRefPubMed
  21. 21.↵
    Burki T. No end in sight for the Brazilian COVID-19 crisis. Lancet Microbe. 2021;2:e180. doi:10.1016/S2666-5247(21)00095-1.
    OpenUrlCrossRefPubMed
  22. 22.↵
    Brasil Ministério da Saúde. Banco de dados do Sistema Único de Saúde-OpenDataSUS; 2022. https://opendatasus.saude.gov.br/dataset/sim-1979-2019;https://opendatasus.saude.gov.br/dataset/sim-2020-2021.
  23. 23.↵
    Patterson HD, Thompson R. Recovery of interblock information when block sizes are unequal. Biometrika. 1971;58:545—-554. doi:10.2307/2334389.
    OpenUrlCrossRefWeb of Science
  24. 24.↵
    Pinheiro JC, Bates D. Mixed-effects models in S and S-PLUS. New York: Springer-Verlag; 2000.
  25. 25.↵
    1. R. Hoboken
    Demidenko E. Mixed models: Theory and applications with R. Hoboken, New Jersey: John Wiley & Sons; 2013.
  26. 26.↵
    Singer JM, Rocha FMM, Nobre JS. Graphical tools for detecting departures from linear mixed model assumptions and some remedial measures. Int Stat Rev. 2017;85:290–324. doi:10.1111/insr.12178.
    OpenUrlCrossRef
  27. 27.↵
    Baey C, Cournede PH, Kuhn E. Asymptotic distribution of likelihood ratio test statistics for variance components in nonlinear mixed effects models. Computational Statistics & Data Analysis. 2019;135:107—-122.
    OpenUrl
  28. 28.↵
    Aron J, Muellbauer J. The US excess mortality rate from COVID-19 is substantially worse than Europe’s; 2020. https://voxeu.org/article/us-excess-mortality-rate-covid-19-substantially-worse-europe-s.
  29. 29.↵
    R Core Team. R: A Language and Environment for Statistical Computing; 2021. Available from: https://www.R-project.org/.
  30. 30.↵
    Pinheiro J, Bates D, DebRoy S, Sarkar D, R Core Team. nlme: Linear and nonlinear mixed effects models; 2021. Available from: https://CRAN.R-project.org/package=nlme.
  31. 31.↵
    Baey C, Kuhn E. varTestnlme: variance components testing in mixed-effect models; 2019. Available from: https://github.com/baeyc/varTestnlme.
  32. 32.↵
    Associação Médica Brasileira. Vacinação COVID-19 no Brasil: Passado, Presente e Desafios Futuros - AMB; 2021. https://amb.org.br/noticias/vacinacao-covid-19-no-brasil-passado-presente-e-desafios-futuros/.
  33. 33.↵
    Institute for Health Metrics and Evaluation - IHME. COVID-19; 2022. https://covid19.healthdata.org/brazil?view=cumulative-deaths&tab=trend.
  34. 34.↵
    The Lancet. COVID-19 in Brazil: “So what?”. Lancet. 2020;395:1461. doi:10.1016/S0140-6736(20)31095-3.
    OpenUrlCrossRefPubMed
  35. 35.↵
    Jardim B, Migowski A, Miranda Corrêa F, Azevedo e Silva G. Covid-19 no Brasil em 2020: impacto nas mortes por câncer e doenças cardiovasculares. SciELO Preprints Collect. 2021;00:2021–2028. doi:10.11606/s1518-8787.2022056004040.
    OpenUrlCrossRef
  36. 36.
    Ng WH, Tipih T, Makoah NA, Vermeulen JG, Goedhals D, Sempa JB, et al. Comorbidities in SARS-CoV-2 patients: a systematic review and meta-analysis. mBio. 2021;12:1–12. doi:10.1128/mBio.03647-20.
    OpenUrlCrossRef
  37. 37.↵
    Izcovich A, Ragusa MA, Tortosa F, Marzio MAL, Agnoletti C, Bengolea A, et al. Prognostic factors for severity and mortality in patients infected with COVID-19: A systematic review. PLoS ONE. 2020;15. doi:10.1371/JOURNAL.PONE.0241955.
    OpenUrlCrossRef
  38. 38.↵
    Prado MF, Paula Antunes BB, Santos Lourenço Bastos L, Peres IT, Araújo Batista Silva A, Dantas LF, et al. Analysis of COVID-19 under-reporting in Brazil. Rev Bras Ter Intensiva. 2020;32:224–228. doi:10.5935/0103-507X.20200030.
    OpenUrlCrossRef
  39. 39.↵
    Kupek E. How many more? Under-reporting of the COVID-19 deaths in Brazil in 2020. Trop Med Int Health. 2021;26:1019–1028. doi:10.1111/tmi.13628.
    OpenUrlCrossRef
  40. 40.↵
    PAHO Incident Management System Team and the PAHO Office for Equity, Gender and Cultural Diversity. COVID-19 Health Outcomes by Sex in the Americas. From January 2020 to January 2021; 2021. https://iris.paho.org/handle/10665.2/53372.
  41. 41.↵
    Aburto JM, Kashyap R, Schöley J, Angus C, Ermisch J, Mills MC, et al. Estimating the burden of the COVID-19 pandemic on mortality, life expectancy and lifespan inequality in England and Wales: a population-level analysis. J Epidemiol Community Health. 2021;75:735–740. doi:10.1136/JECH-2020-215505.
    OpenUrlAbstract/FREE Full Text
  42. 42.↵
    Krieger N, Chen JT, Waterman PD. Excess mortality in men and women in Massachusetts during the COVID-19 pandemic. Lancet. 2020;395:1829. doi:10.1016/S0140-6736(20)31234-4.
    OpenUrlCrossRef
  43. 43.↵
    Michelozzi P, De’Donato F, Scortichini M, Pezzotti P, Stafoggia M, Sario MD, et al. Temporal dynamics in total excess mortality and COVID-19 deaths in Italian cities. BMC Public Health. 2020;20:1–8. doi:10.1186/S12889-020-09335-8.
    OpenUrlCrossRefPubMed
  44. 44.↵
    Kawachi I. COVID-19 and the ‘rediscovery’ of health inequities. Int J Epidemiol. 2020;49:1415–1418. doi:10.1093/IJE/DYAA159.
    OpenUrlCrossRefPubMed
  45. 45.
    Werneck GL. A pandemia de COVID-19: desafios na avaliação do impacto de problemas complexos e multidimensionais na saúde de populações. Cad Saúde Pública. 2022;38:e00045322. doi:10.1590/0102-311xpt045322.
    OpenUrlCrossRef
  46. 46.
    Passos VMA, Brant LCC, Pinheiro PC, Correa PRL, Machado IE, Santos MR, et al. Higher mortality during the COVID-19 pandemic in socially vulnerable areas in Belo Horizonte: Implications for vaccine prioritization. Rev Bras Epidemiol. 2021;24:E210025. doi:10.1590/1980-549720210025.
    OpenUrlCrossRef
  47. 47.↵
    Oliveira RGD, Cunha APD, Gadelha AGDS, Carpio CG, Oliveira RBD, Corrêa RM. Racial inequalities and death on the horizon: COVID-19 and structural racism. Cad Saúde Pública. 2020;36:e00150120. doi:10.1590/0102-311X00150120.
    OpenUrlCrossRef
Back to top
Posted July 29, 2022.
Download PDF
Data/Code
Email
Assessing COVID-19 pandemic excess deaths in Brazil: years 2020 and 2021
Saditt Rocio Robles Colonia, Lara Morena Cardeal, Rogério Antonio de Oliveirax, Luzia Aparecida Trinca
medRxiv 2022.07.27.22278096; doi: https://doi.org/10.1101/2022.07.27.22278096
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area