Classifying sex with MRI

2.1. Characterization of data basis

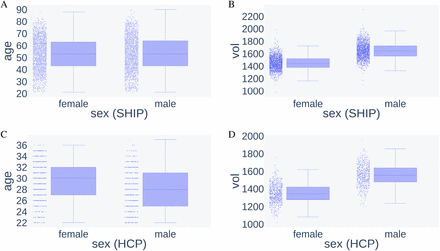
In this study, we used two data sets from two different cohorts, the Human Connectome Project (HCP) and the Study of Health of Pomerania (SHIP). The SHIP data set includes data from the SHIP-2 and the SHIP-TREND-0 cohorts. Both cohorts include participants from the region of West Pomerania, Germany. SHIP-2 examinations were conducted from 2008 to 2012 and for SHIP-TREND-0 from 2008 to 2011 (Völzke et al., 2011). Both SHIP cohorts were pooled together, resulting in a data set of 3308 MRI scans. Participants ages ranged from 21 to 90 years with a mean of 53 years and an almost balanced sex (48.7% self-reported ‘male’ and 51.3% self-reported ‘female’). The overall mean TIV was 1545 ml (978 - 2311 ml), with 1646 ml for male and 1450 ml for female brains. The average TIV of men was 13.5% larger than that of women, matching approximately the aforementioned finding. The SHIP data set was primarily used for training and evaluation of the models.

To assess cross-population performance of the models, we used the HCP S1200 data set of the Human Connectome Project (Van Essen et al., 2013). The HCP data set contains 1113 T1w MRI scans, acquired from 2012 to 2015 on healthy young adults of age 22 – 37 (mean 29) and a near-balanced sex (with 45.5% self-reported males and 54.5% self-reported females). The overall mean TIV was 1441 ml (1017 – 1960 ml), with 1553 ml for male and 15.3% more than the 1347 ml for female brains. See Figure 1 for an illustration of data set properties.

• Download figure
• Open in new tab

Figure 1:

Data set properties age and TIV (vol) in male and female groups of both data sets. A) Age distribution in female and male samples in the SHIP data set. B) TIV distribution in female and male samples in the SHIP data set. C) Age distribution in female and male samples in the HCP data set. D) TIV distribution in female and male samples in the HCP data set.

The primary feature to be assessed by our proposed model was the voxel-wise gray matter volume (GMV) of high resolution T1-weighted anatomical MRI scans. For this purpose, tissue segmentation was performed using the SPM and CAT12 toolboxes running on the MATLAB platform. The following software versions were used: SHIP cohort data SPM v6225, CAT12 v1073; HCP cohort data SPM v7487, CAT12 v1450. At first, a spatial adaptive non-local means (SANLM) denoising filter (Manjón et al., 2010) improved signal-to-noise ratio, which was followed by internal resampling to properly accommodate low-resolution images and anisotropic spatial resolutions. The data were then bias-corrected and affine-registered to further improve the out-comes of the following steps, followed by the standard SPM “unified segmentation” (Ashburner and Friston, 2005). This acted as a starting point for the refinement stage. After skull-stripping, the brain was then parcellated into the left and right hemisphere, subcortical areas, and the cerebellum. Furthermore, local white matter hyperintensities were detected to be later accounted for during the spatial normalization. Subsequently, a local intensity transformation of all tissue classes was performed, which is particularly helpful to reduce the effects of higher gray matter intensities in the motor cortex, basal ganglia, or occipital lobe before the final adaptive maximum a posteriori (AMAP) segmentation. This final AMAP segmentation step (Rajapakse et al., 1997), which is independent of a priori information of the tissue probabilities, was then refined by applying a partial volume estimation (Tohka et al., 2004), which effectively estimates the fractional content for each tissue type per voxel, encoded as a probability value between 0 and 1 for each tissue type. As a last default step, the gray matter (GM) tissue segments were spatially normalized to a common reference space (MNI152 NLIN 6th generation) using DARTEL (Ashburner, 2007) registrations. For the HCP cohort prior to spatial normalization a cohort-specific template was calculated using the DARTEL template creation procedure of SPM. The spatially normalized GM images were modulated in a way, that each voxel encodes the local GMV prior to spatial normalization. As a spatial non-linear normalization removes most of the volume differences to the common template, the local volumetric changes due to this transformation have to be encoded. For this purpose the Jacobian determinant of the local transformations were used to modulate each voxel intensity, which afterwards encode dilation and contraction during that transformation to the common template space. As a result, after spatial normalization, the sum ∑_j X_j of all voxel values of an individual equals his or her total gray matter volume up to small errors in the scale of 1 cm³. Further, then every voxel coordinate of each participant’s GM tissue segment point to the equal anatomical location, enabling the statistical comparison of location and GMV.

Afterwards, a reference template based mask of GM tissue probability (thresholded to 0.5 and binarised) was applied to each single image to retain highly probable GM voxels only. Then, each single image was standardized with a Z-score normalization where μ and σ are the mean and standard deviation of voxel values in the image. Training and classification was performed on the final preprocessed images .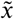

Z-score normalization was important not only as a way of feature scaling for the machine learning algorithms, it also removed the correlation of the sum of voxel values in each image with the TIV. Before Z-score normalization, the voxel sum and TIV showed a positive correlation with Pearson’s correlation coefficient r = 0.645 (see Supplementary Figure 1). Through Z-score normalization, the voxel values in each image sum up to zero, which removes this correlation and is another important measure to rid our data from the nuisance variable TIV.

2.2. Machine learning classifiers

We compared two models for sex prediction, a convolutional neural network (CNN) and logistic regression. Both models are parametrized functions that take as input an image of dimension m = 121 × 145 × 121 and output a ‘femaleness’ score z and a ‘femaleness’ probability p = σ (z) ∈ [0, 1] (see Figure 5), where σ is the logistic sigmoid function, i.e. p = 1/(1 + exp(−z)). We classify a brain as female if and only if p > 0.5 or equivalently if the femaleness score is positive (z > 0) and otherwise as male. The accuracy is computed as the percentage of samples, where the predicted and actual sex agree.

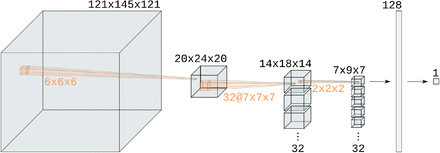
The CNN, that is the basis of our BraiNN model, uses at its core the eponymous 3-dimensional convolutional layer. Further it uses pooling layers, a dropout layer for regularization and two fully-connected (‘dense’) neural network layers as depicted and detailed in Figure 2. The initial pooling layer was added to reduce the number of model parameters. We tried different pooling sizes and found that 6 × 6 × 6 pooling works well and with negligible impact on model performance (data not shown). The dropout rate in the dropout layer was 0.5. The activation function for the convolution and the 128 unit dense layer was PReLU (parametrized rectified linear unit). The second dense layer (the output layer) had a single unit with sigmoid activation function. In total, BraiNN has 1, 930, 625 parameters (or “weights”).

• Download figure
• Open in new tab

Figure 2:

Illustration of BraiNN’s architecture. The layer dimensions are written above the layers, the pooling and filter dimensions in orange. The first layer is the input image, a 121 × 145 × 121 voxel MRI scan with one gray value per voxel. It is followed by a 6 × 6 × 6 max pooling (same stride), resulting in a 20 × 24 × 20 layer. To this, a 7 × 7 × 7 convolution with 32 filters is applied, yielding a 32 × 14 × 18 × 14 layer. This is again max-pooled with 2 × 2 × 2 (stride ‘same’), resulting in a 32 × 7 × 9 × 7 layer. This is flattened and fully connected to a 128 unit dense layer (left arrow). A dropout layer (not shown) with rate 0.5 is applied before the final dense layer (right arrow). The last layer outputs a single unit – the femaleness probability.

Logistic regression (here abbreviated as LogReg) uses weight w_j for each input voxel 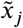as well as a bias ameter w₀ computes the femaleness score very simply as 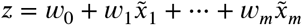and therefore requires to train m + 1 = 2, 122, 946 parameters. As training criterion, the cross entropy error was minimized. The models were implemented using the TensorFlow framework (Abadi et al., 2015). Training used a stochastic gradient descent algorithm (Adam optimizer, learning rate 0.0001).

The BraiNN and LogReg parameters were estimated on the SHIP data set during a 5 × 5-fold cross-validation as described in the next section. BraiNN was trained for 100 epochs on the complete cohort data set and for 200 epochs on the matched data set, LogReg was trained for 30 epochs in both cases.

2.3. Cross validation

We used k × ℓ-fold cross-validation with k = ℓ = 5 for training, validation and evaluation. For this, the SHIP data set was randomly and under the uniform distribution split into five equally sized subsets. We then performed 5 “outer” training rounds, each time with a different one of the five subsets held back as a test set. The respectively remaining four subsets were combined to use for training. In each of the “outer” training rounds, we performed a nested cross validation by again randomly splitting the training data into 5 equally sized subsets. Again, five “inner” training rounds were performed, while holding back each time a different one of the five inner subsets as a validation set. The respectively four remaining inner subsets ((4/5)² = 64% of the data) were combined to the actual training set. We then trained the model on the training set, using the validation set during training to monitor and control the training process. When the loss on the validation set did not decrease significantly (i.e. by more than 0.0001) for more than four epochs, the learning rate was reduced by multiplying it with 0.75. The model weights were stored each time the validation loss reached a new minimum. After training was finished, the model performance was evaluated on the test set. For this, the weights from the point of the lowest validation loss during training were used. At each training round, it is ensured that the test and validation data were not used for parameter estimation and that the test data was never seen during the training procedure. This way, we trained the model 25 times on different random splits of the data set, and report the average performance of the single models on their respective test data as result. Performing cross-validation reduces random effects where a single split of the data into training, validation and test set works particularly good or bad and gives a more confident estimate of how well the model will perform on upcoming new data.

2.4. Human expert classification

We challenged an experienced MRI-researcher and neurologist (author Martin Lotze) to compete against BraiNN in classifying the sex based on a subset of MRI scans. We randomly sampled 100 scans from the SHIP data set. He was allowed to look at the original complete MRI scans but sex information was withheld. We trained BraiNN on the remaining 3208 SHIP images and let it classify the same 100 images as Martin Lotze. BraiNN was only shown preprocessed images as before. The human expert principally had an advantage as the preprocessing for BraiNN removed helpful information such as TIV, head shape and the size of the ventricular system.

2.5. Correction for TIV sex differences through matching

It is well known that brain size, and for that matter body height, correlate with sex (Ruigrok et al., 2014). In fact, the self-reported sex in our SHIP data set can be classified with 80.7% accuracy when simply classifying any scan below a TIV threshold of 1551.91 ml as female and otherwise as male. Accuracies up to about 80% are therefore trivially achievable and irrelevant unless some correction for brain volume is performed.

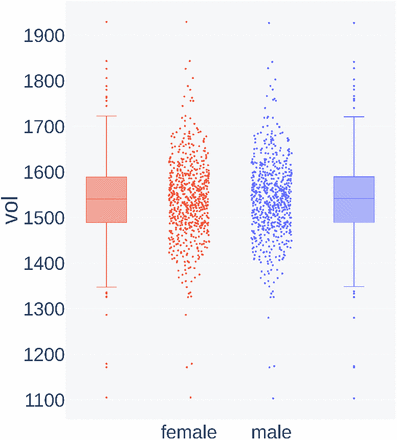
Although the MRI scans are normalized for gray matter volume and should only encode local volume differences, we performed experiments on matched data sets to make sure the model does not benefit even from remains of global brain volume information. For this, the samples of the SHIP data set were grouped by sex and by TIV in steps of 10 ml. For each volume group, the larger of both sex subgroups was identified and a random sample of the same size as the smaller subgroup was taken. This way, we created a reduced ‘matched’ data set of 1274 images in which both sexes have virtually the same TIV distribution, shown in Figure 3, and cannot be distinguished based on that parameter any more.

• Download figure
• Open in new tab

Figure 3:

Distribution of TIV (vol, in cm³) in female and male MR images in the volume-matched data set.

Since the matched data set is much smaller than the complete cohort data set (39%), a reduced performance of a parameter rich model is to be expected simply from the fact that fewer training images were available. To assess this effect, we also created a reduced data set by randomly sampling 1274 images from the complete SHIP data set and trained our models on this reduced data set. To reduce stochastic effects, we repeated the random sub-sampling five times. Each time, training was performed with 5-fold cross validation. Here, the data is again randomly split into five equally sized subsets. Then, in five training rounds, each time a different subset is held back as test set and the remaining subsets are combined into the training set. This time, no validation sets are created for use during training. This way, the models were also trained 25 times on the reduced data set.

2.6. Regions of interest

To investigate the contributions of certain brain regions to the accuracy of sex prediction, we performed occlusion experiments respecting prior neuroanatomical knowledge. For this purpose we created 17 different binary regions of interest (ROI), compiled from 136 labels of the Neuromorphometrics atlas (provided by Neuromorphometrics, Inc. under academic subscription) as included in SPM12 and saved in the same dimensions as the MRI images. See Figure 7 for the list of regions and supplementary file Neuromorphometrics_Derived_ROIs.xlsx for an exhaustive overview. In one experimental setting (‘only ROI’), we applied each ROI mask to each input image in a way that only the respective brain region was left in the image, and the remaining voxels were set to zero. In a second setting (‘masked ROI’), we did the opposite, i.e. only setting the corresponding ROI voxels to zero and leaving the remaining image voxels unchanged. Thus, in the ‘only ROI’ setting, the classification results indicate how well the models perform on just small regions of the brain, and the ‘masked ROI’ classification results indicate, how much the models rely on a brain region. We use the area under the receiver operation characteristics curve (AUC) to evaluate the model performances. In the ‘only ROI’ results, a high AUC for one or more ROIs could indicate that the respective regions are sufficiently different between the sexes. In the ‘masked ROI’ results, a much worse performance compared to the models that used the whole brain images would mean that the respective region was key to successful classification and thus could also indicate that the remaining regions are of low information about the sex.

3.1. Performance using complete cohorts

First we compared the two machine learning classifiers BraiNN and LogReg with each other using all – and therefore unmatched – data of the complete SHIP cohort as described in Section 2.3. Recall, that the spatial non-linear normalization described in Section 2.1 is supposed to control for overall brain size already. The average performances are shown in Table 1. LogReg performed better on the SHIP test data with 94.59% accuracy, but BraiNN also got a high accuracy of 89.78%. This is also mirrored in the area under the receiver operation characteristic curve (AUC). LogReg had an AUC of 0.988, BraiNN of 0.962 on the SHIP test data. Supplementary Figure 2 shows these ROC curves on the left.

The LogReg accuracy is just under the maximum reported accuracy we found in the literature: Feis et al. (2013) had reported a sex classification accuracy of 96%, achieved with a support vector machine. However, their study did not describe any control for overall brain size, indicating this comparison may not be fair. Further, their data set contained only n = 67 + 55 individuals, suggesting a relatively low precision of the accuracy estimate.

3.2. On volume-matched participants

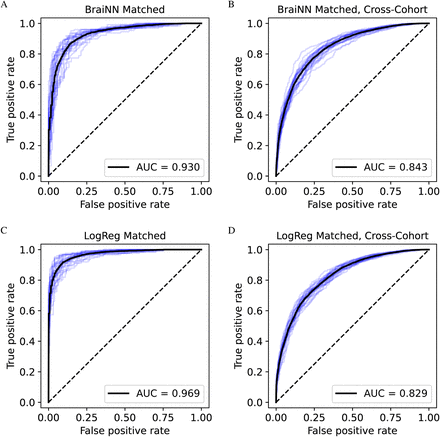
In order to ensure that possible undetected remains of lobal brain volume information in the data do not distort the models, we then used the matched SHIP data set described in Section 2.5 for training of a LogReg and BraiNN. Both methods were evaluated using 5 × 5-fold cross-validation. As can be seen from the results in Table 1, LogReg still performed better on the SHIP test data with an accuracy of 90.91% compared to BraiNN with 86.15%. The AUCs for the matched data set show the same trend as with the complete cohort data set. LogReg has an AUC of 0.969, BraiNN of 0.930. See the left side of Figure 4 for the ROC curves.

• Download figure
• Open in new tab

Figure 4:

Receiver operation characteristic (ROC) curves for BraiNN (CNN) and LogReg on the matched SHIP data set. The ROC curves of each single training run are shown in blue, the black curves are the respective averaged ROC curves. The mean area under the curve (AUC) is shown in the bottom right of the plots. A) ROC and AUC for BraiNN, trained on the matched SHIP data set when predicting the SHIP test data. B) ROC and AUC for BraiNN, trained on the matched SHIP data set when predicting the HCP data set. C) ROC and AUC for LogReg, trained on the matched SHIP data set when predicting the SHIP test data. D) ROC and AUC for LogReg, trained on the matched SHIP data set when predicting the HCP data set.

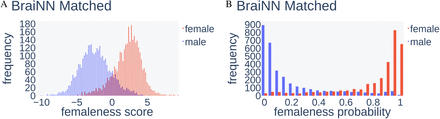
The distribution of the femaleness score z and femaleness probability p output by BraiNN for the test images is shown in Figure 5. The femaleness score distribution for male images peaks at around -3 to -4 and for female images at around +3 to +4, both distributions appear to be approximately normal distributed. BraiNN is correctly and confidently predicting the sex of the majority of test images. There are few extreme cases of women classified as very likely male and vice versa. However, the shape of Figure 5A does not suggest that there is a substantial fraction of label errors, in which case either distribution would be expected to have a second mode. The femaleness probability is correctly close to 0 or 1 for most images and the default classifier threshold of 0.5 appears to be a reasonable choice in this setting.

Previously, Wang et al. (2012) had performed sex classification on a volume-matched data set of only 35 male and 35 female subjects. Their support vector machine had as input combined structural MRI and resting-state fMRI data and obtained a mean classification accuracy of 89%. Our similar accuracy confirms the result that even with a careful gold-standard control for brain volume the sexes can be distinguished quite accurately. Furthermore, our much larger data set of 1274 images allows for more precise estimates of the accuracy and we here used only part of the input features that Wang et al. (2012) had used.

3.3. Influence of training cohort size

Using a volume-matched subset in Section 3.2 reduced the prediction accuracy of both studied methods with respect to using the complete SHIP cohort in Section 3.1. As hypothesized, this could be a consequence of what is sometimes called feature leakage in the machine learning domain. This could be the case if at least partial information from the total brain volume is still represented in the complete cohort data set, even though some normalization method was applied. On the other hand, smaller training sets also generally lead to less accurate models, when their number of parameters is large. To assess the impact of the latter, i.e. of the reduced number of training images, we also trained the models on randomly sampled subsets from the SHIP data set. As one of the subset sizes we chose the size of the matched data set, 1274, in order to make comparisons that allow to disentangle the two expected causes for said difference.

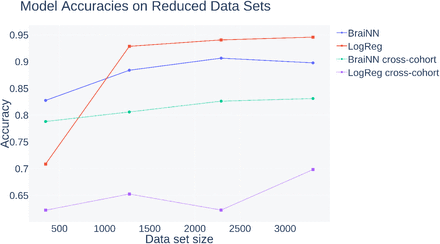
Figure 6 shows the accuracies of our methods as a function of cohort size. Note that with the cross-validation we use, a larger cohort size both allows a better parameter training and a more precise evaluation of the accuracy.

• Download figure
• Open in new tab

Figure 5:

Distribution of femaleness score and femaleness probability from BraiNN on SHIP test images after training on the matched SHIP data set. A) Distribution of the femaleness score, red bars depict the frequency (y axis) of the score (x axis) for female scans, blue for male scans. A score below 0 leads to classification of the image as male, otherwise as female. B) Distribution of the femaleness probability. Scans with a femaleness probability above 0.5 are classified as female.

• Download figure
• Open in new tab

Figure 6:

Influence of the data set size (347, 1274, 2291 and 3308) on the model accuracies. The smaller sized data sets were randomly sampled from the complete cohort data set and training was performed as described in Section 2.5.

• Download figure
• Open in new tab

Figure 7:

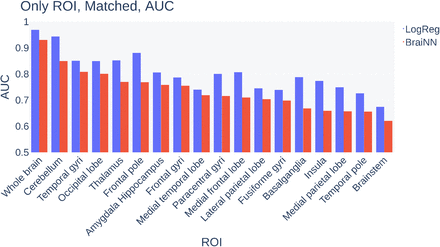
AUC of LogReg and BraiNN for SHIP images of “whole brain” or only a certain ROI. The volume-matched SHIP data set was used for training.

In comparison, the performance on the randomly reduced data set of the same size of the matched data set was 92.87% accuracy for LogReg and 88.40% for BraiNN on the SHIP test data. Thus, less than half of the lost percent points from the whole data set training to the matched data set training can be explained by the reduced training set size. If we subtract the losses due to a smaller (random subset) cohort size from the losses due to using a volume-matched data set, we obtain estimates of the effect of feature leakage: For BraiNN, an estimated (89.78−86.15)−(89.78− 88.4) = 2.25 percent points and for LogReg an estimated (94.59 − 90.91) − (94.59 − 92.87) = 1.96 percent points of the loss in accuracy when using a volume-matched data set rather than a normalization approach can be attributed to an incomplete accounting for TIV. This confirms quantitatively that matching for TIV is the gold standard for removing the influence of body size on brain comparisons between males and females. Naturally, if not done with matching, the choice of a brain-size normalization procedure may have a large influence on sex predictability (Sanchis-Segura et al., 2020).

The leftmost data points in Figure 6 show the accuracy for a data set size of 347, which is the number of children of which Kurth et al. (2021) classified their sex using relevance vector regression (RVR) following a principal component analysis (PCA). On their data set Kurth et al. achieved a classification accuracy of 80.4%. When we downsample our data set to the same size in order to correct for advantages from our larger data set, BraiNN achieves an accuracy of 82.8%. This suggests that our convolutional neural network is competitive with or better than the approach of Kurth et al. (2021).

The solid curves crossing each other in Figure 6 show also very prominently that BraiNN is more accurate than LogReg on smaller data sets below roughly 1000 participants. Logistic regression, as performed by us, looses accuracy very quickly when the cohort size is small and – although better for large cohorts – would likely be noncompetitive for many of the cohort sizes from the relevant literature.

3.4. Cross cohort prediction

A major concern for translation of machine learning (ML) methods to clinical use is their robustness with respect to differences in machines, protocols, preprocessing software and practices. A ML method could perform better than a human expert when applied to data from the same distribution as the data it was trained on but perform poorly and much worse than an expert when applied to data, say, from a different machine. In order to study the robustness of our methods we used a second data set with data from the Human Connectome Project (HCP), which is unrelated to the SHIP cohort and its age distribution is narrower and with a much smaller mean. This allows to assess how well the trained models generalize to new images from a different scanner and population. We then performed within-data set and between-data set experiments. In the first, SHIP images were used both for training and performance evaluation, in the later, SHIP images were used for training and HCP data for performance evaluation. In both cases 5 × 5-fold cross-validation was performed. Table 1 shows the results for logistic regression and our CNN.

As expected, in a cross-cohort prediction the accuracy drops for both methods compared to the within-cohort results (Table 1). When training on the complete SHIP cohort and predicting on HCP, the LogReg performance steeply dropped to 69.83% accuracy (AUC 0.919, see right side of Supplementary Figure 2). In the cross-cohort predictions, BraiNN retained a higher accuracy of 83.11% (AUC 0.927). When trained on the volume-matched SHIP data set, the accuracies on the HCP cohort were 71.45% for LogReg and 73.34% for BraiNN (AUC 0.829 and 0.843, respectively, see right side of Figure 4).

The training set size had a smaller impact when training cross-cohort, presumably as the performance is overall lower and a good fit to the training cohort is not necessarily an advantage (Figure 6). BraiNN is consistently more accurate than LogReg by about 15 percent points, e.g. the HCP performance dropped to 65.26% for LogReg and 80.60% for BraiNN when trained on a random subset of size 1274 of the SHIP data set. Overall these experiments in which BraiNN always performed more accurately than LogReg suggest that our BraiNN convolutional neural network is more robust than logistic regression towards the changes in the data set distribution stemming from changes in the scanner, its software and the population.

3.5. Regions of interest

We performed the ROI experiments on both the complete cohort and matched SHIP data set. We observed overall the same effects in both cases and will therefore only describe the matched data set results in more detail. The other results can be found in the Supplementary Material. Note that in some experiments we found a poor model accuracy but a rather high AUC. For example, using only the cerebellum for training resulted in an accuracy of 0.483 for LogReg when using the default classifier threshold of 0.5 (see Section 2.2), while the AUC was 0.824. Here we observed a tendency to predict values close to zero for both males and females (not shown). With a classifier threshold of 0.5, this then leads to almost every image being predicted as male and thus the poor accuracy. However, the high AUC indicates that LogReg was indeed able to accurately predict the test data with a better suited classifier threshold. We thus here compare the ROIs based on the more meaningful AUC measure rather than the accuracies.

The first experimental setting ‘only ROI’, where only one region is ’visible’ to the classifier, revealed that for both models any of the investigated single brain regions are enough to classify brains with an AUC of at least 0.620. While slightly better than random guessing, this is a poor performance compared to the whole brain images, where LogReg and BraiNN achieve 0.969 and 0.930, respectively. However, some single ROIs performed quite well on their own. Especially the cerebellum showed the highest AUC for both models with 0.943 and 0.849 for LogReg and BraiNN, respectively. When classifying the HCP data set, the cerebellum also performed best with an AUC of 0.824 and 0.759 for LogReg and BraiNN (whole brain images: 0.829 (LogReg) and 0.843 (BraiNN)). See Figure 7 for a bar plot comparing the AUC of the “whole brain” images and the single ROIs for both models. Supplementary Figure 3 shows a bar plot of the model performances on the HCP data set. The exact values are shown in Supplementary Table 2. Other regions with an AUC > 0.8 (LogReg, BraiNN) were temporal gyri (0.850, 0.808) and occipital lobe (0.849, 0.801).

The second experimental setting (‘masked ROI’) showed for both models and both training data sets only slight differences in model AUC, i.e. leaving out any ROI could be compensated by the models and performed almost as good as when the whole brain was input. See the Supplementary Material for bar plots illustrating the different AUCs for “whole brain” images and images with masked ROIs for both models and both training data sets, and the performances on the cross cohort data (Suplementary Figures 2, 4 and 6). The exact values are shown in Supplementary Tables 3 and 4.

3.6. Machine versus human expert

Of the 100 test scans given both to BraiNN and Martin Lotze, BraiNN correctly classified 87 scans and ML correctly classified 62 scans. 36 images were correctly classified by the program and not by the expert, whereas 11 images were correctly classified by the human and not by the program, 51 were correctly predicted by both. BraiNN is more accurate at sex classification than this expert (p < 0.0004, two-sided sign test).

Limitations of the study

The ROIs we chose for the occlusion experiments are rather coarse. Further examinations could possibly improve interpretability by using a finer partition of the brain or a ’searchlight’ approach (Weaverdyck et al., 2020). Another limitation is that the sex attribute was self-reported and not complemented by sex-specific measurements, such as those of testosterone or oestrogen. We carefully excluded the information that brain size holds on sex. Also, male and female individuals had very similar age distributions in the SHIP cohort. Furthermore, the broad differentiation of ROI-specific recognition rates are an argument that neuroanatomy is indeed the factor modulating correct classification. However, another limitation is that we cannot exclude the possibility that some other further attribute of individuals – unknown to us or unrecognized – correlates with sex, is detectable in MR images but is irrelevant to the question how male and female brains differ principally.