Short Telomeres and a T-Cell Shortfall in COVID-19: The Aging Effect

James J. Anderson, Ezra Susser, Konstantin G. Arbeev, Anatoliy I. Yashin, Daniel Levy, Simon Verhulst, Abraham Aviv
doi: https://doi.org/10.1101/2021.05.19.21257474

Abstract

The slow pace of global vaccination and the rapid emergence of SARS-CoV-2 variants suggest recurrent waves of COVID-19 in coming years. Therefore, understanding why deaths from COVID-19 are highly concentrated among older adults is essential for global health. Severe COVID-19 T-cell lymphopenia is more common among older adults, and it entails poor prognosis. Much about the primary etiology of this form of lymphopenia remains unknown, but regardless of its causes, offsetting the decline in T-cell count during SARS-CoV-2 infection demands fast and massive T-cell clonal expansion, which is telomere length (TL)-dependent. We have built a model that captures the effect of age-dependent TL shortening in hematopoietic cells and its effect on T-cell clonal expansion capacity. The model shows that an individual with average hematopoietic cell TL (HCTL) at age twenty years maintains maximal T-cell clonal expansion capacity until the 6th decade of life when this capacity plummets by more than 90% over the next ten years. The collapse coincides with the steep increase in COVID-19 mortality with age. HCTL metrics may thus explain the vulnerability of older adults to COVID-19. That said, the wide inter-individual variation in HCTL across the general population means that some younger adults with inherently short HCTL might be at risk of severe COVID-19 lymphopenia and mortality from the disease.

Significance Statement Declining immunity with advancing age is a general explanation for the increased mortality from COVID-19 among older adults. This mortality far exceeds that from viral illnesses such as the seasonal influenza, and it thus requires specific explanations. One of these might be diminished ability with age to offset the development of severe T-cell lymphopenia (a low T-cell count in the blood) that often complicates COVID-19. We constructed a model showing that age-dependent shortening of telomeres might constrain the ability of T-cells of some older COVID-19 patients to undertake the massive proliferation required to clear the virus that causes the infection. The model predicts that individuals with short telomeres, principally seniors, might be at a higher risk of death from COVID-19.

Introduction

Transient lymphopenia is a common feature of acute viral respiratory infections (1). The drastic and prolonged lymphopenia of COVID-19, however, is distinctive and largely stems from falling counts of T cells (2-5). Regardless of the still poorly understood primary causes of this T-cell lymphopenia (2,3), the decline in T-cell count in COVID-19 demands fast and massive T-cell clonal expansion, which is telomere length (TL)-dependent (6,7). As hematopoietic cell TL (HCTL) shortens with age (8), T-cells from some older adults might lack the clonal expansion capacity required to offset the development of COVID-19 lymphopenia or recover from it (9). These individuals, we hypothesize, are at a higher risk of developing COVID-19 T-cell lymphopenia and severe disease.

In absence of an acute infection, the T cell turnover is slow because of the relatively long biological half-lives of naïve T cells and memory T cells in the circulation, i.e., ∼ 5 years and ∼ 5 months, respectively (10). In the face of SARS-CoV-2 infection, however, diminished TL-dependent T-cell proliferative capacity in older adults could result in a shortfall between T-cell depletion and repletion (11). Moreover, the clearance of SARS-CoV-2 requires clonal expansion and differentiation of naïve T cells into SARS-CoV-2 antigen-specific effector/memory (henceforth memory) T cells (2,3,5). Short naïve T-cell telomeres might thus limit adaptive immunity against the virus even without infection-mediated T-cell lymphopenia. We therefore modelled the relationships of TL-dependent T-cell clonal expansion capacity with age and virtually examined its relation to COVID-19 mortality in the general population.

Results

Note: Abbreviations, symbols and units used in the mathematical development of the model are presented in Box 1.

Box 1.

Abbreviations, meanings, units and values

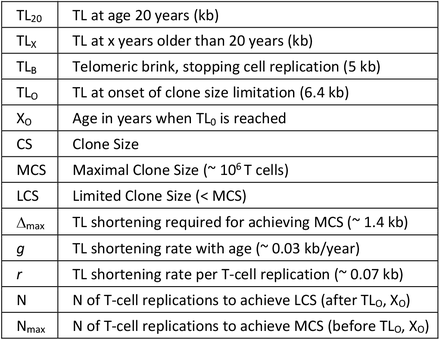
Figure

The following assumptions on T-cell replication and T-cell clone size (CS) drive our model (Fig. 1a): (i) T-cell TL-dependent cessation of replication is defined by a “telomeric brink” (TLB) that stops replication at 5 kilobases (8). (ii) TL of a naïve T cell at age 20 years (TL20) progressively shortens at a rate g of 0.03 kb/year (12,13) until it reaches the TLB. (iii) In exponential growth, i.e., 1→ 2→ 4→ 8→16, etc., a single naïve T cell can generate a maximal CS (MCS) of ∼ 106 (one million) memory T cells through ∼ 20 replications (Nmax); this value was estimated based on the ∼ 1.4 kb TL difference between circulating naïve and memory T cells and the ∼ 0.07 kb telomere shortening per replication of cultured T cells (14). (iv) We denote the maximal TL shortening due to clonal expansion as Δmax and the TL shortening per replication as r. (v) Due to age-dependent TL shortening, a naïve T-cell TL reaches the “telomeric onset” (TLO = 6.4 kb) at “age of onset” (XO). Until XO, a naïve T cell can generate MCS. After XO, a naïve T cell can generate only a limited clonal size (LCS < MCS), as the TL of the clonal cells converges to the TLB. (vi) Most memory T cells are formed in response to new antigens during childhood and early adulthood (15), when HCTL is comparatively long (16-18), enabling the achievement of MCS.

Fig. 1.
Fig. 1. Age-dependent T-cell telomere length (TL) and its relation to T-cell clonal expansion.

a displays age-dependent TL before Embedded Image and after Embedded Image clonal expansion. Naïve T-cell clonal expansion shortens telomeres by Δ, where Δmax is T-cell telomere shortening resulting from expansion to form the maximal clonal size (MCS). The telomeric brink (TLB) of 5 kb is TL that increases the risk of cessation of replication. TL20 is TL at 20 years, TLO is telomeric onset, which indicates the shortest T-cell TL that enables attaining MCS. XO is age of onset of clonal expansion limitation. b displays T-cell clonal expansion size vs age from onset XO. Circle areas depict relative clonal size in 2-year intervals after XO. Light blue circle is MCS.

We define CS by the number (N) of T-cell replications producing CS = 2N. As a clone expands, TL of its T cells progressively shortens, i.e., Δ= rN, where r is the telomere shortening due to T-cell replication. Prior to XO, the maximum number of T-cell replications in clonal expansion is Nmax = Δmax/r = 20. After XO, the number of T-cell replications in clonal explansion is N = (TLX − TLB)/r, where X designates age and the corresponding age-dependent TL of a naïve T cell is TLX = TL20 − g (X − 20), where g is the TL shortening in the naïve T cell each year. The resulting XO is the number of years it takes for a naïve T cell to reach TLO. 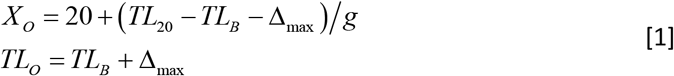These measures are defined: Embedded Image

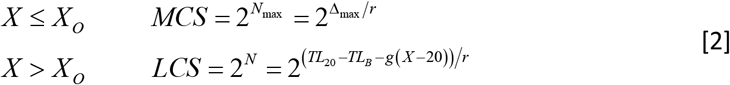
The clone size depends on age relative to XO as follows: Embedded Image

Note that after XO, while TL continues to shorten at its slow pace of 0.03 kb/year below TLO of 6.4 kb (Fig. 1a), the clonal expansion capacity of T cells plummets exponentially. Consequently, in one decade after XO, the clonal expansion capacity of naive T cells is 5% of MCS (Fig. 1b).

The following considerations are relevant for appraising the model’s parameters and assumptions: First, while the MCS is based on the in vivo TL difference between naïve and memory T cells, the data on telomere shortening per T-cell replication are from cultured cells (14). A similar approach (based on data from circulating hematopoietic cells and telomere shortening in cultured cells) was previously used to generate consistent information on hematopoietic cell replicative kinetics (19,20). Second, the model’s TL parameters are derived from a large population-based study (8) that measured HCTL by Southern blotting (21). Its telomere data are consistent with another large-scale study that used Flow-FISH to measure HCTL (18). Third, the model is based on age-dependent shortening of HCTL and not T-cell TL. As TL differences among leukocyte lineages within the individual are far smaller than the inter-individual HCTL variation (22), T-cell TL largely mirrors HCTL. Fourth, the TL signal for cessation of cell replication originates from the shortest telomeres in the nucleus and not their mean TL (23,24). Using the Telomeres Shortest Length Assay (TeSLA), a method that tallies and measures the shortest telomeres (25), we recently showed that in patients with COVID-19 the shortest telomeres in peripheral blood mononuclear cells were associated with low lymphocyte counts (11). The principles that drive our model thus likely apply to the T cell’s shortest telomeres.

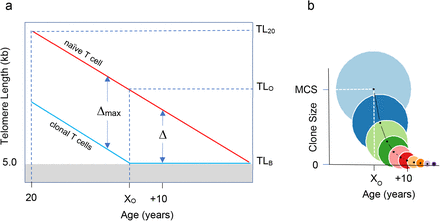
Consider now three individuals with average, long (one SD above the mean) and short (one SD below the mean) naïve T-cell TL20 (Fig. 2a) whose TL shortens with age (Fig. 2b): Up to XO of 50 years, the naive T cells of the individual with the average TL20 can attain the MCS of ∼106 cells. Thereafter, however, the ability of these naïve T cells to clonally expand declines in an exponential manner from the MCS to 0.43 x 106, 0.24 x 106 and 0.13 x 106 cells at ages 53, 55 and 57 years, respectively (Fig. 2c). Next consider the individual with long T-cell TL20 (Fig. 2a). The ability of naive T-cells of this individual to achieve MCS extends to the XO of 70 years (Fig. 2c). This suggests that even among older adults, some individuals can develop MCS when infected with SARS-CoV-2. In contrast, naïve T cells of the individual with short T-cell TL20 are able to achieve MCS only until the XO of 30 years (Fig. 2c), inferring that some young adults might generate a poor T-cell response to SARS-CoV-2 infection. Our model thus suggests that in the overwhelming majority of the general population, naïve T cells can achieve MCS before early adulthood. Later, post XO, while age-dependent shortening of T-cell telomeres remains slow (Figs. 1a and 2b), it has a striking effect on clonal expansion of naïve T cells because the exponential nature of the process (Figs. 1b and 2c).

Fig. 2.
Fig. 2. Population distribution of T-cell TL at age 20 (TL20), T-cell TL shortening with age, and age-dependent change in T-cell clone size (CS).

a displays the TL20 distribution, showing mean TL = 7.3 kb Embedded Image, long TL (mean + SD) = 7.9 kb Embedded Image, and short TL (mean – SD) = 6.7 kb Embedded Image. b displays age-dependent change in T-cell for mean, long and short TL20. Past the telomeric onset (TLO = 6.4 kb), TL is insufficient to produce MCS because a full clonal expansion drops TL below the telomeric brink (TLB = 5 kb). The TLO is reached at different ages of onset (XO), i.e., an older age for T-cells with long T-cell telomeres and younger with T-cells with short telomeres. The age-dependent T-cell TL shortening (0.03 kb/year) for T cells with mean, long and short telomeres at TL20 is shown by the lines. c shows that the T-cell CS is partitioned by the XO into plateau and slope regions. T cells with mean, long or short TL20 achieve MCS on the CS plateau, but their CS exponentially collapses (slope) once their TLs shorten below TLO of 6.4 kb and exceed XO (at different ages).

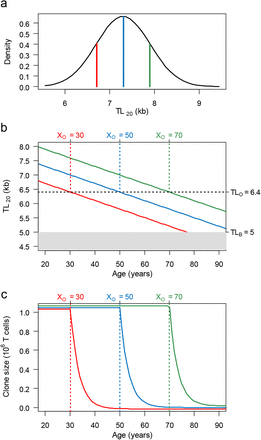
With aging, T cells of an increasing proportion of the population reach XO (Fig. 3a). After reaching this TL landmark, LCS contracts rapidly to < 1% of MCS over 16 years. This rapid LCS contraction means that at any age, the individuals largely separate into two sub-populations: those with naïve T cells that can generate MCS and those with naïve T cells that can only generate LCS, which a few years after XO is a small fraction of MCS. While naïve T cells of individuals in their twenties can overwhelmingly generate MCS, naïve T cells of most individuals in their seventies can at best generate clones that are typically less than one tenth of MCS (Fig. 3b).

Fig. 3.
Fig. 3. Shifts by age in naïve T-cell TL distribution and relative frequency (0 to 10) of T-cell clone size (CS) in the population.

a displays the shift in TL20 distribution (Fig. 2a) resulting from age-dependent shortening of 0.03 kb/year. It depicts TL < TLO (6.4 kb) by blue bars Embedded Image and TL > TLO by red bars Embedded Image. b displays relative frequency of CS’s generated by naïve T-cell clonal expansion corresponding to the categories of TL below or above TLO. It shows that maximal CS (MCS) of ∼ 106 cells occurs in individuals with naïve T-cell TL > TLO, while limited CS (LCS) occurs in those with naïve T-cell TL ≤ TLO. At age 20, naïve T cells of nine out of ten individuals can generate MCS. At age 70, naïve T cells of less than two out of ten individuals can generate MCS, and seven out of ten generate clone sizes that are less than 0.1 MCS. At age 50 the population is approximately equally divided between the MCS and LCS groups.

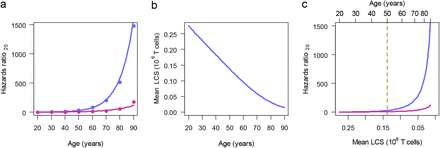
What then might be the minimal TL-dependent T-cell CS that enables survival of an individual contracting COVID-19? The definitive answer awaits telomere and T-cell data in populations of COVID-19 patients. That said, we infer this CS based on Centers for Disease Control and Prevention (CDC) reports of the age-specific COVID-19 mortality rates for the United States (26) and the population size by age in 2019 (27). We computed an age-dependent hazards ratio of mortality relative to age 20 years (Hazards20) from COVID-19 and from general causes (27) other than COVID-19 (Methods). The Hazards20 yields an exponential increase of COVID-19 mortality with age, and for comparison, we also display Hazards20 for mortality from non-COVID-19 causes (Fig. 4a).

Fig. 4.
Fig. 4. Steps linking mean limited clone size (LCS) to COVID-19 mortality and general mortality Hazards ratios20 in the population.

a displays data based on COVID-19 mortality Embedded Image and non-COVID-19 mortality Embedded Image, and corresponding exponential fitted relationships for Hazards ratios20 (Embedded Image and Embedded Image). b displays the relationship of mean LCS in units of 106 cells with age, generated with Eq. 2, using the TL20 distribution of Fig. 2a. c displays the relationships of Hazards ratios20 generated from COVID-19 mortality and non-COVID-19 mortality plotted against mean LCS obtained from b. The top of the panel also displays age. The divergence between the COVID-19 and non-COVID-19 mortalities occurs at mean LCS of ∼ 0.13 x 106 T cells. At the corresponding age, 50 years, the population is about evenly divided into the LCS and MCS sub-populations (Fig. 3b). After this age, the majority of the population is in the LCS subpopulation, which is susceptible to COVID-19 mortality, whereas the MCS group is not.

We assumed that, as a subpopulation, individuals who generate MCS experience no T-cell TL-related COVID-19 mortality. We therefore calculated the mean CS for the LCS subpopulation only, i.e., adults older than XO (Fig. 3a). The TL-limited clonal expansion of individuals in the LCS subpopulation, we assumed, might contribute to their propensity to die from COVID-19, given the association between lymphopenia and COVID-19 mortality. Fig. 4b shows that the mean LCS in adults older than XO decreases in a near linear manner with age. Plots of the mean LCS vs. Hazards ratios20 of COVID-19 mortality and non-COVID-19 mortality suggests a divergence between the two trajectories during the 6th decade (Fig. 4c). The figure also displays the mean LCS at the age of 50 years, which corresponds to the age at which the size of LCS subpopulation is similar to that of the MCS subpopulation (Fig. 3b). Mean LCS at this age amounts to ∼ 0.13 x 10−6 T cells.

The divergence of COVID-19 mortality from non-COVID-19 mortality when the mean LCS is about one tenth of MCS suggests the following: In the absence of COVID-19, ∼ 10% MCS is generally sufficient to accommodate the low turnover of T-cells (10). This LCS, however, might contribute to mortality in the face of SARS-CoV-2, because the infection demands massive T-cell clonal expansion to offset the primary cause of the dropping naïve T-cell count, and to generate memory T-cells that clear the virus.

Although our model is deterministic with fixed rates selected as best estimates from available literature, analyses reveals that uncertainty in the parameters and assumptions on the LCS cutoff definition have little effect on model conclusions. In SI Appendix A1 an analysis of the propagation of error from r, g, TLB and Δmax indicate a 1.5% uncertainty in TLO and ∼ 3.5 years uncertainty in XO (Fig. S1a). The uncertainty in N and CS are significant prior to XO but decline afterwards (Fig. S1b, c). However, the properties of the model are expressed in terms of the ratio of CS/MCS, so the model properties are independent of the absolute value of MCS.

The comparison of the COVID-19 and non-COVID-19 Hazards ratio20 (Fig. 4) assumes that COVID-19 mortality only occurred for CS < MCS. Correspondingly, other LCS cutoff levels, e.g., < 0.5 MCS or < 0.15 MCS, result in different relationships of LCS, hazards ratio20 and age. SI Appendix A2 explores these relationships with alternative LCS cutoff levels. Alternative cutoffs have a minor effect on the percent of the population assigned to the LCS group (Fig. S2a) and therefore the cutoff has little effect on the distribution of the COVID-19-susceptible population with age as characterized by the bar colors in Fig. 3. However, the slope of mean LCS vs age declines with lower cutoff levels (Fig. 2b), which in turn compresses the hazards ratio20 curve vs the mean LCS (Fig. S2c). Consequently, the cutoff level changes the critical mean LCS at which the COVID-19 and non-COVID-19 hazards ratios20 diverge but this critical level is proportional to the cutoff level. Thus, a significant divergence of COVID-19 and non-COVID-19 hazards ratios20 is robust to the definition of the CS level susceptible to mortality.

Discussion

With the exception of heritability (28), no other single factor so profoundly affects HCTL as does aging, explaining the key conclusion of our model. As SARS-CoV-2 memory T cells play a greater role than neutralizing antibodies in recovering from the infection (5), the aging effect on HCTL could impede adaptive immunity and heighten the risk for severe COVID-19. Moreover, we assume that MCS of ∼106 cells applies not only for naïve T cells that clonally expand to produce memory T cells but also naïve T cells that clonally expand to produce naïve T cells. This means that regardless of the primary cause of COVID-19 T-cell lymphopenia, the T cell response after XO will be compromised on two levels, i.e., formation of SARS-CoV-2-specific memory T-cells and replenishing the loss of naïve T-cells.

As illustrated in Figs. 2 and 3, our model might also apply to naïve T cells of a small subset of younger adults, whose HCTL is ranked at the lower range of the HCTL distribution in the general population (8,18). Comparatively short HCTL might also diminish naïve T-cell clonal expansion in response to SARS-CoV-2 infection in males, whose HCTL is shorter than in females from birth onwards (8,16,18,28), persons with atherosclerotic cardiovascular disease (29), obese persons and smokers (31,32), whose HCTL is respectively shorter than that in healthy, lean and non-smoking individuals. All these individuals with shorter HCTL are at a higher risk of severe COVID-19 and death from the disease (33-37).

Humans have comparatively short telomeres relative to their long lifespan (38,39), and therefore our model may not apply to most terrestrial mammals, including laboratory animal models that are used for viral research. For instance, TL-mediated replicative aging is probably not consequential during the 2-3-year lifespan of mice, considering their long telomeres (mean TL > 30 kb) and robust telomerase activity in their somatic cells. In contrast, the average human TL at birth is only ∼ 9.5 kb (16). As telomerase activity is repressed in replicating human somatic cells, their short telomeres experience further age-dependent shortening after birth. Although naïve T cells have some telomerase activity, it is insufficient to prevent their age-dependent telomere shortening, and aging may thus undermine the T-cell clonal expansion in many older humans. Whereas lymphopenia is a major prognostic feature of COVID-19 in older adults, when present, it is transient and of little prognostic value in children (40-42). The longer HCTL during early life potentially explain this clinical course.

Relatedly, the model shows that naïve T-cells with TL20 of one SD below the mean are unable to achieve MCS as early as after the third decade of life. This unexpected finding suggests that (a) under-estimation of naïve T-cell TL using population-based HCTL data, or (b) in response to pathogens, more naïve T cells might be tapped for clonal expansion (43) in young adults with short T-cell telomeres. Older adults may not have sufficient naïve T cells, particularly, naïve CD8 T cells, for this purpose (44).

We acknowledge the following limitations: The model draws on HCTL data from populations comprising principally whites of European ancestry in high-income countries. It should also be tested in populations of different ancestries and in low- and middle-income countries. The TL difference between naïve T cells and memory T cells likely reflects the clonal expansion in response to not only a single encounter but multiple encounters with a given antigen and its cross-reactive antigens. Thus, the MCS and LCS definitions in absolute T-cell numbers might be off the mark. Of note, however, the MCS and LCS can be expressed in the model in relative units of MCS (i.e., 0.5 MCS, 0.25 MCS, etc.) rather than absolute units (i.e., 0.5 x 106, 0.25 x 106 T cells, etc.), yielding identical results to those based on absolute T-cell numbers. Therefore, the principles of our model are likely to hold notwithstanding the above limitations.

In conclusion, the TL effect on naïve T-cell clonal expansion probably influences the outcome of SARS-CoV-2 infection. The insight generated by our model might set the stage for measurement of TL parameters not only in older adults but also the general adult population, helping to identify individuals vulnerable to severe COVID-19 because of short T-cell telomeres. These individuals might also be less likely to develop a lasting T-cell-mediated adaptive immunity in response to anti-SARS-CoV-2 vaccines. Finally, the ramifications of these conclusions go beyond the influence of TL on T-cell response to SARS Cov-2 infection and vaccination against the virus. They suggest that TL might be a limiting factor in immunotherapies whose efficacies depend on clonally expanding (in vivo and in vitro) transplanted hematopoietic cells, chimeric antigen receptor T cells, and tumor-infiltrating lymphocytes.

Materials and Methods

The relationships between the age-dependent T-cell TL density and the relative proportion of CS in a population (Fig. 3) were derived from the distribution of HCTL at age twenty, extrapolated from age-specific density plots of HCTL (8). In Fig. 3a, the T-cell TL distribution for age 20 was derived from 1,000,000 random generations from a normal distribution with a mean = 7.3 kb and SD = 0.6 kb.

The combined male and female hazards ratios relative to age 20 in Fig. 4a were calculated from age-specific COVID-19-linked mortalities and total non-COVID-19 linked mortalities normalized by the age-specific US population. The hazards ratios, defined Hazards20 = (mortalityage/populationage)/(mortality20/population20), are based on the CDC records of 494,234 provisional COVID-19 deaths and 3,845,819 total deaths between January 1, 2020 through March 8, 2021 (26) and the 2019 US Census (27). Non-COVID-19 mortalities were estimated by subtracting the COVID-19 mortalities from the total mortalities for each age group.

R Code for generating the figures is provided in SI Appendix B.

Data Availability

Data used in paper is available in supplemental material

Disclaimer

The views expressed in this manuscript are those of the authors and do not necessarily represent the views of the National Heart, Lung, and Blood Institute; the National Institutes of Health; or the U.S. Department of Health and Human Services.

Supplementary Information

A1. Effects of parameter estimates on model response

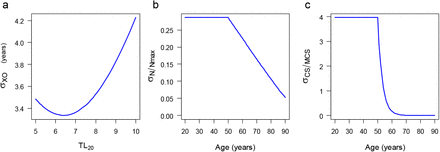
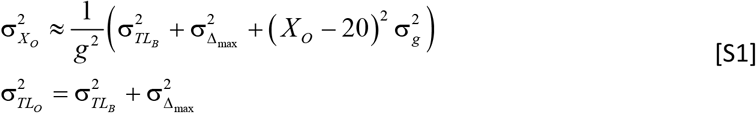
Parameters (MCS, LCS, XO, TLO, g, r, TLB, TL20, and Δmax, Box 1 in the paper) were derived from published data (Table S1 shows references). To demonstrate the contribution of these terms to the model uncertainty, we use the propagation of error approach assuming uncorrelated terms. Based on the equation XO = 20 + (TL20 − TLB − Δmax)/g the uncertainty in the TLO measures is Embedded Image

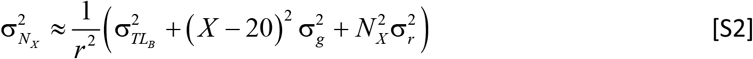
To estimate uncertainty of CS, first define the number of T-cell replications in clone expansion as NX = (TL20 − g (X − 20) − TLB)/r where age is X. Then variance in replications is Embedded Image

Next, to estimate uncertainty in CS, define clone size in terms of number of replications as 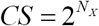Embedded Image, then the variance in the CS for a clone with limited expansion ability is Embedded Image and the variance on MCS is calculated from equation (S3) by setting X to XO giving Embedded Image

The uncertainties for these measures are calculated using the parameter estimates and standard deviations given in Table S1.

The uncertainty in the TL of the TLO from Eq. [S1] is 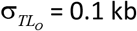Embedded Image kb, or 1.5%. The uncertainty in XO depends on TL20. Fig. S2a shows that the uncertainty varies slightly with TL20. Using the population mean TL20 of 7.3 kb the uncertainty is 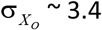Embedded Image years.

The uncertainty in CS and number of replications depend on age X (Fig. S2 b, c). In the figures the uncertainty is normalized by measures prior to TLO, i.e., Nmax = 20 and MCS = 220. In panels b and c, the relative uncertainties decrease after the TLO, here set to XO = 50 years to represent individuals with average TL20 of 7.3 kb. Notably, the large uncertainty in the MCS is wholly dominated by σr through Eq.[S2]. While the uncertainty in CS is significant, the properties of the model are expressed in terms of the ratio CS/MCS and not the actual value of MCS.

Fig. S1.
Fig. S1.

Uncertainty in parameter estimates. (a) Uncertainty in XO with TL20. (b) Uncertainty in clone replication number (N) with age normalized by Nmax. (c) Uncertainty with age in CS normalized by the MCS.

View this table:
Table S1. Parameter estimates and uncertainties.

A2. Effect of limited clone size (LCS) definition on model response and correlation with observed mortality

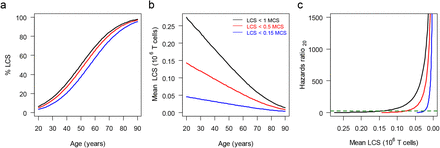
The model assumes that mortality from COVID-19 only occurs when T-cell clonal expansion cannot achieve maximum clone size (MCS). We were unable to a priori select how LCS might affect mortality. We explored instead the relationship of mean LCS with years and the Hazards ratio20 for three cutoff levels used for defining LCS: (I) LCS < MCS, (II) LCS < 0.5 MCS, and (III) LCS < 0.15 MCS (Fig. S2). In cutoff I, any clone that cannot achieve a MCS is included in the LCS subpopulation and therefore susceptible to COVID-19 mortality. In cutoff II, only clones that are less than half the MCS are included in the LCS subpopulation and in cutoff III only clones that are less than 15% of the MCS are included.

The percent of the subpopulation in the LCS category (%LCS) increases from ∼ 5% at age 20 to ∼ 90% at age 90 (Fig. S2a). These percentages change little between the three cutoff levels. The maximum difference in % LCS in the definitions occurs at age 50 years. This close tracking with age indicates that the LCS cutoff has a minimal effect on the partition of the subpopulations in Figs. 3a and b. Note that the height of the histogram bars in Fig. 3b does not depend on the LCS cutoff.

Fig. S2b illustrates that the LCS cutoff has a strong effect on the mean LCS pattern with age. But for all cutoffs the mean LCS declines in a nearly linear manner with age. Thus, the assumption of a linear age-dependence of mean LCS with age is unaffected by the LCS cutoff choice.

Fig. S2c depicts the effect of the LCS cutoff on the Hazard ratio20. Here, because the cutoffs do not significantly affect linearity of mean LCS with age, they rescale the mean LCS at which the Hazards ratio20 of COVID-19 and non-COVID-19 diverge, which for Fig. 4c is taken as the critical Hazards ratio20 = 25.4. Then the mean LCS associated with this critical Hazards ratio20 linearly scales with the LCS cutoff as 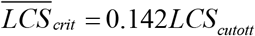Embedded Image.

Fig. S2.
Fig. S2.

Model properties with three LCS cutoff levels: LCL < 1.0 MCS (―), LCL < 0.5 MCS Embedded Image and LCL < 0.15 MCS Embedded Image. (a) % of population in LCS group by age for cutoff levels, (b) mean LCS vs age for cutoff levels, (c) Hazards ratio20 vs mean LCS for cutoff levels. Dashed line Embedded Image depicts Hazards ratio20 (25.4) at which COVID-19 and non-COVID-19 mortalities diverge.

Acknowledgments

AIY and KGA research is supported by NIH grant RF1AG046860. SV human telomere research is funded NIH grant 5U24AG066528. AA telomere research is supported by NIH grants R01 HL134840, U01AG066529 and a grant from the Norwegian Research Council (NFR) ES562296.

Footnotes

  • Author Contributions: J.J.A. and A.A. designed research and wrote paper; J.J.A. created and tested the model; S.V., E.S., K.G.A., A.I.Y., D.L. contributed to writing the paper.

  • Competing Interest Statement: No competing interests.

  • Declining immunity with advancing age is a general explanation for the increased mortality from COVID-19 among older adults. This mortality far exceeds that from viral illnesses such as the seasonal influenza, and it thus requires specific explanations. One of these might be diminished ability with age to offset the development of severe T-cell lymphopenia (a low T-cell count in the blood) that often complicates COVID-19. We constructed a model showing that age-dependent shortening of telomeres might constrain the ability of T-cells of some older COVID-19 patients to undertake the massive proliferation required to clear the virus that causes the infection. The model predicts that individuals with short telomeres, principally seniors, might be at a higher risk of death from COVID-19.

References

  1. 1.↵
    McClain, M.T., Park, L.P., Nicholson B, Veldman T, Zaas AK, Turner R, Lambkin-Williams R, Gilbert AS, Ginsburg GS, Woods CW. Longitudinal analysis of leukocyte differentials in peripheral blood of patients with acute respiratory viral infections. J Clin Virol. 58, 689– 95 (2013).
    OpenUrlCrossRefPubMed
  2. 2.↵
    Sette, A., Crotty, S. Adaptive immunity to SARS-CoV-2 and COVID-19. Cell. 12, S0092- 8674(21)00007-6. doi: 10.1016/j.cell.2021.01.007. Online ahead of print. PMID: 33497610 (2021).
    OpenUrlCrossRefPubMed
  3. 3.↵
    Chen Z, John Wherry E. T cell responses in patients with COVID-19. Nat Rev Immunol. 2020 Sep;20(9):529–536. doi: 10.1038/s41577-020-0402-6. Epub 2020 Jul 29. PMID: 32728222
    OpenUrlCrossRefPubMed
  4. 4.
    Diao B, Wang C, Tan Y, Chen X, Liu Y, Ning L, Chen L, Li M, Liu Y, Wang G, Yuan Z, Feng Z, Zhang Y, Wu Y and Chen Y (2020) Reduction and Functional Exhaustion of T Cells in Patients With Coronavirus Disease 2019 (COVID-19). Front. Immunol. 11:827. doi: 10.3389/fimmu.2020.00827
    OpenUrlCrossRefPubMed
  5. 5.↵
    Rydyznski Moderbacher C, Ramirez SI, Dan JM, Grifoni A, Hastie KM, Weiskopf D, Belanger S, Abbott RK, Kim C, Choi J, Kato Y, Crotty EG, Kim C, Rawlings SA, Mateus J, Tse LPV, Frazier A, Baric R, Peters B, Greenbaum J, Ollmann Saphire E, Smith DM, Sette A, Crotty S. Antigen-Specific Adaptive Immunity to SARS-CoV-2 in Acute COVID-19 and Associations with Age and Disease Severity. Cell. 2020 Nov 12;183(4):996-1012.e19. doi: 10.1016/j.cell.2020.09.038. Epub 2020 Sep 16. PMID: 33010815
    OpenUrlCrossRefPubMed
  6. 6.↵
    Patrick M, Weng NP. Expression and regulation of telomerase in human T cell differentiation, activation, aging and diseases. Cell Immunol. 2019 Nov; 345:103989. doi: 10.1016/j.cellimm.2019.103989. Epub 2019 Sep 19. Review. PMID: 31558266
    OpenUrlCrossRefPubMed
  7. 7.↵
    Hodes RJ, Hathcock KS, Weng NP. Telomeres in T and B cells. Nat Rev Immunol. 2002 Sep;2(9):699-706. Review. PMID: 12209138
    OpenUrlCrossRefPubMedWeb of Science
  8. 8.↵
    Steenstrup T, Kark JD, Verhulst S, Thinggaard M, Hjelmborg JVB, Dalgård C, Kyvik KO, Christiansen L, Mangino M, Spector TD, Petersen I, Kimura M, Benetos A, Labat C, Sinnreich R, Hwang SJ, Levy D, Hunt SC, Fitzpatrick AL, Chen W, Berenson GS, Barbieri M, Paolisso G, Gadalla SM, Savage SA, Christensen K, Yashin AI, Arbeev KG, Aviv A. Telomeres and the natural lifespan limit in humans. Aging (Albany NY). 2017 Apr;9(4):1130–1142. doi: 10.18632/aging.101216. PMID: 28394764
    OpenUrlCrossRefPubMed
  9. 9.↵
    Aviv A. Telomeres and COVID-19. FASEB J. 2020 Jun;34(6):7247–7252. doi: 10.1096/fj.202001025. Epub 2020 May 19. PMID: 32427393
    OpenUrlCrossRefPubMed
  10. 10.↵
    Vrisekoop N, den Braber I, de Boer AB, Ruiter AF, Ackermans MT, van der Crabben SN, Schrijver EH, Spierenburg G, Sauerwein HP, Hazenberg MD, de Boer RJ, Miedema F, Borghans JA, Tesselaar K. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc Natl Acad Sci U S A. 2008 Apr 22;105(16):6115–20. doi: 10.1073/pnas.0709713105. Epub 2008 Apr 17. PMID: 18420820
    OpenUrlAbstract/FREE Full Text
  11. 11.↵
    Benetos A, Lai TP, Toupance S, Labat C, Verhulst S, Gautier S, Ungeheuer MN, Perret-Guillaume C, Levy D, Susser E, Aviv A. The Nexus between Telomere Length and Lymphocyte Count in Seniors hospitalized with COVID-19. J Gerontol A Biol Sci Med Sci. 2021 Feb 2:glab026. doi: 10.1093/gerona/glab026. Online ahead of print. PMID: 33528568
    OpenUrlCrossRefPubMed
  12. 12.↵
    Steenstrup T, Hjelmborg JV, Kark JD, Christensen K, Aviv A. The telomere lengthening conundrum--artifact or biology? Nucleic Acids Res. 2013 Jul;41(13):e131. doi: 10.1093/nar/gkt370. Epub 2013 May 13. PMID: 23671336
    OpenUrlCrossRefPubMed
  13. 13.↵
    Nettle D, Gadalla SM, Lai TP, Susser E, Bateson M, Aviv A. Telomere length measurement for longitudinal analysis: implications of assay precision. Am J Epidemiol. 2021 Feb 10:kwab025. doi: 10.1093/aje/kwab025. Online ahead of print. PMID: 33564874
    OpenUrlCrossRefPubMed
  14. 14.↵
    Weng NP, Hathcock KS, Hodes RJ. Regulation of telomere length and telomerase in T and B cells: a mechanism for maintaining replicative potential. Immunity. 1998 Aug;9(2):151–7. doi: 10.1016/s1074-7613(00)80597-x. PMID: 9729035
    OpenUrlCrossRefPubMedWeb of Science
  15. 15.↵
    Farber DL, Yudanin NA, Restifo NP. Human memory T cells: generation, compartmentalization and homeostasis. Nat Rev Immunol. 2014 Jan;14(1):24–35. doi: 10.1038/nri3567. Epub 2013 Dec 13. PMID: 24336101
    OpenUrlCrossRefPubMed
  16. 16.↵
    Factor-Litvak P, Susser E, Kezios K, McKeague I, Kark JD, Hoffman M, Kimura M, Wapner R, Aviv A. Leukocyte Telomere Length in Newborns: Implications for the Role of Telomeres in Human Disease. Pediatrics. 2016 Apr;137(4):e20153927. doi: 10.1542/peds.2015-3927. Epub 2016 Mar 11. PMID: 26969272
    OpenUrlAbstract/FREE Full Text
  17. 17.
    Benetos A, Verhulst S, Labat C, Lai TP, Girerd N, Toupance S, Zannad F, Rossignol P, Aviv Telomere length tracking in children and their parents: implications for adult onset diseases. FASEB J. 2019 Dec;33(12):14248–14253. doi: 10.1096/fj.201901275R. Epub 2019 Oct 25. PMID: 31652401
    OpenUrlCrossRefPubMed
  18. 18.↵
    Aubert G, Baerlocher GM, Vulto I, Poon SS, Lansdorp PM. Collapse of telomere homeostasis in hematopoietic cells caused by heterozygous mutations in telomerase genes. PLoS Genet. 2012;8(5):e1002696. doi: 10.1371/journal.pgen.1002696. Epub 2012 May 17. PMID: 22661914
    OpenUrlCrossRefPubMed
  19. 19.↵
    Sidorov I, Kimura M, Yashin A, Aviv A. Leukocyte telomere dynamics and human hematopoietic stem cell kinetics during somatic growth. Exp Hematol. 2009 Apr;37(4):514–24. doi: 10.1016/j.exphem.2008.11.009. Epub 2009 Feb 12. PMID: 19216021
    OpenUrlCrossRefPubMedWeb of Science
  20. 20.↵
    Shepherd BE, Guttorp P, Lansdorp PM, Abkowitz JL. Estimating human hematopoietic stem cell kinetics using granulocyte telomere lengths. Exp Hematol. 2004 Nov;32(11):1040–50. doi: 10.1016/j.exphem.2004.07.023. PMID: 15539081
    OpenUrlCrossRefPubMedWeb of Science
  21. 21.↵
    Kimura M, Stone RC, Hunt SC, Skurnick J, Lu X, Cao X, Harley CB, Aviv A. Measurement of telomere length by the Southern blot analysis of terminal restriction fragment lengths. Nat Protoc. 2010 Sep;5(9):1596–607. doi: 10.1038/nprot.2010.124. Epub 2010 Sep 2. PMID: 21085125
    OpenUrlCrossRefPubMedWeb of Science
  22. 22.↵
    Kimura M, Gazitt Y, Cao X, Zhao X, Lansdorp PM, Aviv A. Synchrony of telomere length among hematopoietic cells. Exp Hematol. 2010 Oct;38(10):854–9. doi: 10.1016/j.exphem.2010.06.010. Epub 2010 Jun 25. PMID: 20600576
    OpenUrlCrossRefPubMedWeb of Science
  23. 23.↵
    Hemann MT, Strong MA, Hao LY, Greider CW. The shortest telomere, not average telomere length, is critical for cell viability and chromosome stability. Cell. 2001;107(1):67–77. Epub 2001/10/12. doi: 10.1016/s0092-8674(01)00504-9. PubMed PMID: 11595186.
    OpenUrlCrossRefPubMedWeb of Science
  24. 24.↵
    Zou Y, Sfeir A, Gryaznov SM, Shay JW, Wright WE. Does a sentinel or a subset of short telomeres determine replicative senescence? Mol Biol Cell. 2004;15(8):3709–18. Epub 2004/06/08. doi: 10.1091/mbc.e04-03-0207. PubMed PMID: 15181152; PMCID: PMC491830.
    OpenUrlAbstract/FREE Full Text
  25. 25.↵
    Lai TP, Zhang N, Noh J, Mender I, Tedone E, Huang E, Wright WE, Danuser G, Shay JW. A method for measuring the distribution of the shortest telomeres in cells and tissues. Nat Commun. 2017;8(1):1356. Epub 2017/11/09. doi: 10.1038/s41467-017-01291-z. PubMed PMID: 29116081; PMCID: PMC5676791
    OpenUrlCrossRefPubMed
  26. 26.↵
    CDC. 2021. Deaths involving coronavirus disease 2019 (COVID-19) reported to NCHS by sex and age group and week ending date. (https://data.cdc.gov/NCHS/Provisional-COVID-19-Death-Counts-by-Sex-Age-and-W/vsak-wrfu/data).
  27. 27.↵
    CB. 2019. 2019: ACS 1-year estimates subject tables. Survey/Program: American Community Survey TableID: S0101. U.S. Census Bureau. (https://data.census.gov/cedsci/all?q=S0101).
  28. 28.↵
    Hjelmborg JB, Dalgård C, Möller S, Steenstrup T, Kimura M, Christensen K, Kyvik KO, Aviv The heritability of leucocyte telomere length dynamics. J Med Genet. 2015 May;52(5):297–302. doi: 10.1136/jmedgenet-2014-102736. Epub 2015 Mar 13.PMID: 25770094
    OpenUrlAbstract/FREE Full Text
  29. 29.↵
    Benetos A, Toupance S, Gautier S, Labat C, Kimura M, Rossi PM, Settembre N, Hubert J, Frimat L, Bertrand B, Boufi M, Flecher X, Sadoul N, Eschwege P, Kessler M, Tzanetakou IP, Doulamis IP, Konstantopoulos P, Tzani A, Korou M, Gkogkos A, Perreas K, Menenakos E, Samanidis G, Vasiloglou-Gkanis M, Kark JD, Malikov S, Verhulst S, Aviv A. Short Leukocyte Telomere Length Precedes Clinical Expression of Atherosclerosis: The Blood- and-Muscle Model. Circulation Research. 2018;122(4):616–23. Epub 2017/12/16. doi: 10.1161/circresaha.117.311751. PubMed PMID: 29242238; PMCID: PMC5821479.
    OpenUrlAbstract/FREE Full Text
  30. 30.
    Valdes AM, Andrew T, Gardner JP, Kimura M, Oelsner E, Cherkas LF, Aviv A, Spector TD. Obesity, cigarette smoking, and telomere length in women. Lancet. 2005;366(9486):662–4. Epub 2005/08/23. doi: 10.1016/s0140-6736(05)66630-5. PubMed PMID: 16112303, PMC2810865.
    OpenUrlCrossRefPubMedWeb of Science
  31. 31.↵
    Nawrot TS, Staessen JA, Gardner JP, Aviv A. Telomere length and possible link to X chromosome.Lancet. 2004 Feb 14;363(9408):507–10. PMID: 14975611
    OpenUrlCrossRefPubMedWeb of Science
  32. 32.↵
    Bateson M, Aviv A, Bendix L, Benetos A, Ben-Shlomo Y, Bojesen SE, Cooper C, Cooper R, Deary IJ, Hägg S, Harris SE, Kark JD, Kronenberg F, Kuh D, Labat C, Martin-Ruiz CM, Meyer C, Nordestgaard BG, Penninx Bwjh, Pepper GV, Révész D, Said MA, Starr JM, Syddall H, Thomson WM, van der Harst P, Whooley M, von Zglinicki T, Willeit P, Zhan Y, Nettle D. Smoking does not accelerate leucocyte telomere attrition: a meta-analysis of 18 longitudinal cohorts. R Soc Open Sci. 2019 Jun 5;6(6):190420. doi: 10.1098/rsos.190420. eCollection 2019 Jun. PMID: 31312500
    OpenUrlCrossRefPubMed
  33. 33.↵
    Nimgaonkar I, Valeri L, Susser E, Hussain S, Sunderram J, Aviv A. The age pattern of the male-to-female ratio in mortality from COVID-19 mirrors that of cardiovascular disease in the general population. Aging (Albany NY). 2021 Feb 7;13(3):3190–3201. doi: 10.18632/aging.202639. Epub 2021 Feb 7. PMID: 33550276
    OpenUrlCrossRefPubMed
  34. 34.
    Promislow DEL. A Geroscience Perspective on COVID-19 Mortality. J Gerontol A Biol Sci Med Sci. 2020 Sep 16;75(9):e30–e33. doi: 10.1093/gerona/glaa094.PMID. 32300796
    OpenUrlCrossRef
  35. 35.
    Bae S, Kim SR, Kim MN, Shim WJ, Park SM. Impact of cardiovascular disease and risk factors on fatal outcomes in patients with COVID-19 according to age: a systematic review and meta-analysis. Heart. 2021 Mar;107(5):373–380. doi: 10.1136/heartjnl-2020-317901. Epub 2020 Dec 17. PMID: 33334865
    OpenUrlAbstract/FREE Full Text
  36. 36.
    Popkin BM, D. S, Green WD, Beck MA, Algaith T, Herbst CH, Alsukait RF, Alluhidan M, Alazemi N, Shekar M. Individuals with obesity and COVID-19: A global perspective on the epidemiology and biological relationships. Obes Rev. 2020 Nov;21(11):e13128. doi: 10.1111/obr.13128. Epub 2020 Aug 26. PMID: 32845580
    OpenUrlCrossRefPubMed
  37. 37.↵
    Patanavanich R, Glantz SA. Smoking Is Associated With COVID-19 Progression: A Meta-analysis. Nicotine Tob Res. 2020 Aug 24;22(9):1653–1656. doi: 10.1093/ntr/ntaa082. PMID: 32399563
    OpenUrlCrossRefPubMed
  38. 38.↵
    Gomes NMV, Oliver A. Ryder, Marlys L. Houck, Suellen J. Charter, William Walker, Nicholas R. Forsyth, Steven N. Austad, Chris Venditt, Mark Pagel, Jerry W Shay, Woodring E. Wright. Comparative biology of mammalian telomeres: hypotheses on ancestral states and the roles of telomeres in longevity determination. Aging Cell. 2011 Oct; 10(5): 761–768. Published online 2011 Jun 1. doi: 10.1111/j.1474-9726. PMCID: PMC3387546
    OpenUrlCrossRefPubMedWeb of Science
  39. 39.↵
    Calado RT, Dumitriu B. Telomere dynamics in mice-and humans. Semin Hematol. 2013 Apr;50(2):165–74. doi: 10.1053/j.seminhematol.2013.03.030. PMID: 23956466
    OpenUrlCrossRefPubMed
  40. 40.↵
    Du H, Dong X, Zhang JJ, Cao YY, Akdis M, Huang PQ, Chen HW, Li Y, Liu GH, Akdis CA, Lu XX, Gao YD. Clinical characteristics of 182 pediatric COVID-19 patients with different severities and allergic status. Allergy. 2020 Jun 10:10.1111/all.14452. doi: 10.1111/all.14452. Online ahead of print. PMID: 32524611
    OpenUrlCrossRefPubMed
  41. 41.
    Ma X, Liu S, Chen L, Zhuang L, Zhang J, Xin Y. The clinical characteristics of pediatric inpatients with SARS-CoV-2 infection: A meta-analysis and systematic review. J Med Virol. 2020 Jun 19:10.1002/jmv.26208. doi: 10.1002/jmv.26208. Online ahead of print. PMID: 32558955
    OpenUrlCrossRefPubMed
  42. 42.↵
    Zachariah P, Johnson CL, Halabi KC, Ahn D, Sen AI, Fischer A, Banker SL, Giordano M, Manice CS, Diamond R, Sewell TB, Schweickert AJ, Babineau JR, Carter RC, Fenster DB, Orange JS, McCann TA, Kernie SG, Saiman L; Columbia Pediatric COVID-19 Management Group. Epidemiology, Clinical Features, and Disease Severity in Patients With Coronavirus Disease 2019 (COVID-19) in a Children’s Hospital in New York City, New York. JAMA Pediatr. 2020 Jun 3:e202430. doi: 10.1001/jamapediatrics.2020.2430. Online ahead of print. PMID: 32492092
    OpenUrlCrossRefPubMed
  43. 43.↵
    Mayer A, Zhang Y, Perelson AS, Wingreen NS. Regulation of T cell expansion by antigen presentation dynamics. Proc Natl Acad Sci U S A. 2019 Mar 26;116(13):5914–5919. doi: 10.1073/pnas.181280011. PMID: 30850527
    OpenUrlAbstract/FREE Full Text
  44. 44.↵
    Goronzy JJ, Weyand CM. Mechanisms underlying T cell ageing. Nat Rev Immunol. 2019 Sep;19(9):573–583. doi: 10.1038/s41577-019-0180-1. Epub 2019 Jun 11. PMID: 31186548; PMCID: PMC7584388.
    OpenUrlCrossRefPubMed

SI References

  1. 1.
    T. Steenstrup, J. V. Hjelmborg, J. D. Kark, K. Christensen, A. Aviv, The telomere lengthening conundrum--artifact or biology? Nucleic Acids Res 41, e131 (2013).
    OpenUrlCrossRefPubMed
  2. 2.
    Aviv et al., Impartial comparative analysis of measurement of leukocyte telomere length/DNA content by Southern blots and qPCR. Nucleic Acids Res 39, e134-e134 (2011).
  3. 3.
    N. P. Weng, K. S. Hathcock, R. J. Hodes, Regulation of telomere length and telomerase in T and B cells: a mechanism for maintaining replicative potential. Immunity 9, 151–157 (1998).
    OpenUrlCrossRefPubMedWeb of Science
  4. 4.
    T. Steenstrup et al., Telomeres and the natural lifespan limit in humans. Aging 9, 1130– 1142 (2017).
    OpenUrl
Back to top
Posted July 10, 2021.
Download PDF
Data/Code
Email
Short Telomeres and a T-Cell Shortfall in COVID-19: The Aging Effect
James J. Anderson, Ezra Susser, Konstantin G. Arbeev, Anatoliy I. Yashin, Daniel Levy, Simon Verhulst, Abraham Aviv
medRxiv 2021.05.19.21257474; doi: https://doi.org/10.1101/2021.05.19.21257474
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area