Visible and real sizes of the COVID-19 pandemic in Ukraine

Igor Nesteruk
doi: https://doi.org/10.1101/2021.03.19.21253938

ABSTRACT

To simulate how the number of COVID-19 cases increases versus time, various data sets and different mathematical models can be used. In particular, previous simulations of the COVID-19 epidemic dynamics in Ukraine were based on smoothing of the dependence of the number of cases on time and the generalized SIR (susceptible-infected-removed) model. Since real number of cases is much higher than the official numbers of laboratory confirmed ones, there is a need to assess the degree of data incompleteness and correct the relevant forecasts. We have improved the method of estimating the unknown parameters of the generalized SIR model and calculated the optimal values of the parameters. It turned out that the real number of diseases exceeded the officially registered values by about 4.1 times at the end of 2020 in Ukraine. This fact requires a reassessment of the COVID-19 pandemic dynamics in other countries and clarification of world forecasts.

Introduction

The studies of the COVID-19 pandemic dynamics are complicated by incomplete information about the number of patients (e.g., reported by WHO [1]), a very large percentage of whom are asymptomatic. In the early stages of the pandemic, there was also a lack of tests and knowledge about the specifics of the infection spread. Because of this, there are more and more evidences of COVID-19 patient appearances before the first officially-confirmed cases [2-6]. These hidden periods of the epidemics in different countries and regions were estimated in [7-11] with use of the classical SIR model [12-14] and the statistics-based method of the parameter identification developed in [15, 16]. In particular, first COVID-19 cases probably have appeared already in August 2019 [9-11].

For Ukraine, different simulation and comparison methods were based on official accumulated number of laboratory confirmed cases [17, 18] (these figures coincided with the official WHO data sets [1], but WHO stopped to provide the daily information in August 2020) and the data reported by Johns Hopkins University (JHU) [19]. In particular simple comparisons of epidemic outbreaks in Ukraine neighboring countries can be found in [20-22]. The classical SIR model was used in [7-11, 23-25]. The weakening of quarantine restrictions, changes in the social behavior and the coronavirus activity caused changes in the epidemic dynamics and corresponding parameters of models. To detect and simulate these new epidemic waves, a simple method of numerical differentiations of the smoothed number of cases and generalized SIR model were proposed and used in [11, 26-30]. In particular, nine epidemic waves in Ukraine were calculated [11, 26-30]. Since the Ukrainian national statistics does not look complete (see, e.g., the results of total staff testing in two schools and two children gardens in the Ukrainian city of Chelnytskii, [31]), there is a need to assess the extent of this incompleteness and determine the true size of the COVID-19 epidemic in Ukraine, which became the subject of this article.

Data

We will use the data set regarding the accumulated numbers of confirmed COVID-19 cases in Ukraine from national sources [17, 18]. The corresponding numbers Vj and moments of time tj (measured in days) are shown in the supplementary Table A. It must be noted that this table does not show all the COVID-19 cases occurred in Ukraine. Many infected persons are not identified, since they have no symptoms. For example, employees of two kindergartens and two schools in the Ukrainian city of Chmelnytskii were tested for antibodies to COVID-19, [31]. In total 292 people work in the surveyed institutions. Some of the staff had already fallen ill with COVID-19 or were hospitalized. Therefore, they were tested and registered accordingly. In the remaining tested 241 educators, antibodies were detected in 148. Therefore, the number of identified patients (51) in these randomly selected institutions was 3.9 times less than the actual number (51+148) of COVID-19 cases. Many people know that they are ill, since they have similar symptoms as other members of families, but avoid making tests. Unfortunately, one laboratory confirmed case can correspond to several other cases which are not confirmed and displayed in the official statistics. The number of cases in Ukraine reported by COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [19] is 2-3 % higher than the Ukrainian national statistics [17, 18] yields (see [30]). Nevertheless, the special simulations will demonstrate a significant incompleteness of both data sets.

Generalized SIR model

The classical SIR model for an infectious disease [12-14] was generalized in [11, 27-30] to simulate different epidemic waves. We suppose that the SIR model parameters are constant for every epidemic wave, i.e. for the time periods: 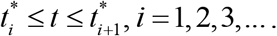Embedded Image Than for every wave we can use the equations, similar to [12-14]: Embedded Image Embedded Image Embedded Image Here S is the number of susceptible persons (who are sensitive to the pathogen and not protected); I is the number of infected persons (who are sick and spread the infection); and R is the number of removed persons (who no longer spread the infection; this number is the sum of isolated, recovered, dead, and infected people who left the region). Parameters αi and ρi are supposed to be constant for every epidemic wave.

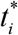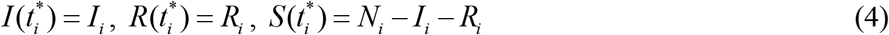
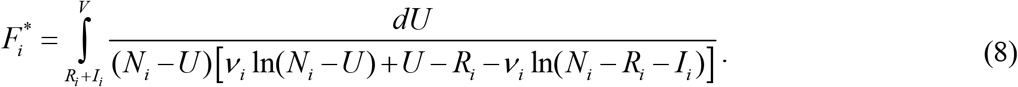
To determine the initial conditions for the set of equations (1)–(3), let us suppose that at the beginning of every epidemic wave Embedded Image: Embedded Image Embedded Image In [11, 27-30] the set of differential equations (1)-(3) was solved by introducing the function Embedded Image corresponding to the number of victims or the cumulative confirmed number of cases. For many epidemics (including the COVID-19 pandemic) we cannot observe dependencies S(t), I(t) and R(t) but observations of the accumulated number of cases Vj corresponding to the moments of time tj provide information for direct assessments of the dependence V (t). The corresponding analytical formulas for this exact solution can be written as follows: Embedded Image Embedded Image Embedded Image Thus, for every set of parameters Ni, Ii, Ri, νi and a fixed value of V, integral (8) can be calculated and the corresponding moment of time can be determined from (7). Then functions I(t) and R(t) can be easily calculated with the use of formulas (9). The saturation levels Si∞; Vi∞= Ni− Si∞ (corresponding the infinite time moment) and the final day of the i-th epidemic wave (corresponding the moment of time when the number of persons spreading the infection will be less then 1) can be calculated with the use of equations available in [11, 27-30].

Parameter identification procedure

In the case of a new epidemic, the values of its parameters are unknown and must be identified with the use of limited data sets. For the second and next epidemic waves (i > 1), the moments of time 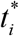Embedded Image corresponding to their beginning are known. Therefore the exact solution (7)-(9) depend only on five parameters - Ni, Ii, Ri,νi, αi, when the registered number of victims Vj is the random realization of its theoretical dependence (6). If we assume, that data set Vj is incomplete and there is a constant coefficient βi ≥ 1, relating the registered and real number of cases during the i-th epidemic wave: Embedded Image the number of unknown parameters increases by one.

Then the values Vj, corresponding to the moments of time tj and relationship (10) can be used in eq. (8) in order to calculate 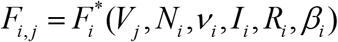Embedded Image for every fixed values of βi, Ni, νi, Ii, Ri and then to check how the registered points fit the linear dependence (7) which can be rewritten as follows: 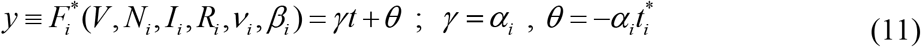Embedded Image We can calculate the parameters γ and θ, by treating the values 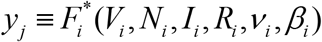Embedded Image and corresponding time moments tj as random variables. 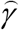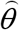Then we can use the observations of the accumulated number of cases and the linear regression in order to calculate the coefficients Embedded Image and Embedded Image of the regression line Embedded Image using the standard formulas (see, e.g., [32]). 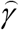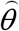Values Embedded Image and Embedded Image can be treated as statistics-based estimations for parameters γ and θ from relationships (11).

The reliability of the method can be checked by calculating the correlation coefficients ri (see e.g., [13]) for every epidemic wave and checking how close are their values is to unity. We can use also the F-test [13] for the null hypothesis that says that the proposed linear relationship (11) fits the data set. Similar approach was used in [7-11, 15, 16, 23-30, 33, 34]. To calculate the optimal values of parameters βi, Ni, νi, Ii, Ri, we have to find the maximum of the correlation coefficient for the linear dependence (11).

The exact solution (7)-(9) allows avoiding numerical solutions of differential equations (1)-(3) and significantly reduces the time spent on calculations. A new algorithm [11, 29, 30] allows estimating the optimal values of SIR parameters for the i-th epidemic wave directly (without simulations of the previous waves). To reduce the number of unknown parameters, we can use the relationship Vi= Ii+ Ri which follows from (6) and (10). 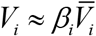To estimate the value Vi, we can use the smoothed accumulated number of cases [11, 26-30] Embedded Image and the relationship Embedded Image following from (10) (i corresponds to the moment of time 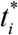Embedded Image). One more relationship Embedded Image can be obtained with the use of (5) and formula Embedded Image (following from (2) and (3)). To estimate the average number of new cases dV/dt at the moment of time 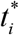Embedded Image in eq. (14), we can use the numerical differentiation of (13): Embedded Image and relationship (10). Thus we have only three independent parameters βi, Niand νi. To calculate the value of parameter αi, some iterations can be used (see details in [11]).

Results

The optimal values of parameters and other characteristics of the ninth COVID-19 pandemic wave in Ukraine are listed in Table 1 for two cases. For SIR simulations we have used the same period of time Tc: December 11-24, 2020 and corresponding values of Vj and tj from Table A. In the first case we assumed that the numbers of registered cases coincide with the real one (β9 =1). A similar SIR simulation of the 9th epidemic wave in Ukraine has already been reported in [30], but now we have managed to find a new (larger in value) maximum of the correlation coefficient.

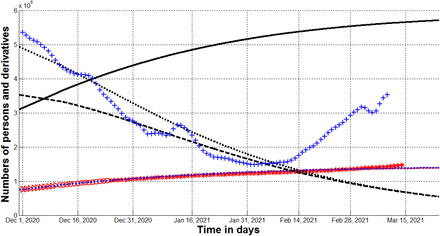
Figure.
Figure. Visible (red) and real (black) COVID-19 epidemic dynamics in Ukraine.

Red markers show accumulated numbers of cases Vj from Table A. “Circles” correspond to the accumulated numbers of cases taken for calculations (during period of time Tc); “triangles” – numbers of cases before Tc; “stars” – number of cases after Tc. Blue and black colors correspond to the case β9 =4.1024; the blue “crosses” show derivative (16) multiplied by 100β9; the blue dotted line represents dependence I (t) / β9. Numbers of victims V(t)=I(t)+R(t) – black solid lines; numbers of infected and spreading I(t) multiplied by 5 – dashed; derivatives dV/dt (eq. (15)) multiplied by 100 – dotted. The red dotted line represents dependence I (t) / β9 for the case β9 =1.

View this table:
Table 1.

Calculated optimal values of SIR parameters and other characteristics of the ninth COVID-19 pandemic wave in Ukraine.

The last column of Table 1 illustrate the results of SIR simulations with the non-prescribed value

of β9. The maximum of the correlation coefficient was achieved at β9 =4.1024. This result testifies that the main part of the epidemic in Ukraine is invisible. At the end of 2020 the real numbers of COVID-19 cases probably were more than 4 times higher than registered ones. The real final size of the ninth epidemic wave V9∞is expected to be around 6 million. Unfortunately, we cannot wait for the end of the pandemic before the summer of 2022 (if vaccinations will not change this sad trend).

Knowing the optimal values of parameters, the corresponding SIR curves can be easily calculated with the use of exact solution (7)-(9) and compared with the pandemic observations after Tc. The results are shown in Figure by different colors. Black and blue lines and markers correspond to the case β9 =4.1024. The solid black line shows complete accumulated number of cases (visible and invisible); the dashed line represents the complete number of infected persons multiplied by 5, i.e. I(t)x5; dotted black line represent the derivative dV/dt (which is an estimation of the real daily number of new cases) calculated with the use of (15) and multiplied by 100. The red dotted line shows the dependence V(t) for the case β9 =1 (assuming that all the cases are registered). The red “circles”, “triangles”, and “stars” correspond to the accumulated numbers of cases registered during period of time taken for SIR simulations Tc, before Tc, and after Tc, respectively (taken from Table A). The blue dotted line represents dependence I (t) / β9. The blue crosses show the estimation of the derivative (16) multiplied by 100β9.

Discussion

According to the results of our study, we can only say that in the case of suitability of the generalized SIR model, the value β9 =4.1024 and other optimal values of its parameters (given in the last column of Table 1) are the most reliable (provide the maximum value of the correlation coefficient). Therefore, we used additional methods to verify the calculations and showed some results in Fig. The blue dotted line represents dependence I (t) / β9 which must be close to the registered number of cases (red markers). The coincidence is very good. Significant deviations began to appear only in March 2021, which can be explained by the beginning of the next (tenth) epidemic wave in Ukraine. The blue crosses show the estimation of the real daily number of new cases (derivative (16) multiplied by 100β9) and have to be close to the black dotted line. Significant deviations began to appear only in mid-February 2021, which can be explained canceling the lockdown on January 24, 2021. May be the beginning of the tenth epidemic wave is connected also with the starting the lessons at schools and universities and mutations of the coronavirus.

The calculated coefficient of epidemic visibility β9 =4.1024 correlates with the results of testing employees of two kindergartens and two schools in the Ukrainian city of Chmelnytskii [31] which revealed the value 3.9. Probably that large discrepancy between registered and actual number of cases occurred not only in Ukraine. For example, total testing in Slovakia (65.5% of population was tested on October 31-November 1, 2020) revealed a number of previously undetected cases, equal to about 1% of the population [35]. On November 7 next 24% of the population was tested and found 0.63% of those infected [36]. According to the WHO report at the end of October, the number of detected cases in Slovakia was also approximately 1% of population [1].

Many authors are and will be trying to predict the COVID-19 pandemic dynamics in many countries and regions [7-11, 16, 23-30, 37-102]. The results of this study indicate that reliable estimates of its dynamics require consideration of incomplete data and constant changes of the conditions (quarantine restrictions, social distancing, coronavirus mutations, etc.).

Data Availability

Data are in the Text

Supplementary materials

View this table:
Table A.

Cumulative numbers of laboratory confirmed Covid-19 cases in Ukraine Vj according to the national statistics, [7, 8].

Acknowledgements

The author is grateful to Oleksii Rodionov for his help in collecting and processing data.

References

  1. 1.↵
    World Health Organization. “Coronavirus disease (COVID-2019) situation reports”. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/. Retrieved Oct. 3, 2020.
  2. 2.↵
    Li, Q., Guan, X., Wu, P., et al. “Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia.” The New England journal of medicine, 2020 Jan. 29. doi:10.1056/NEJMoa2001316.
    OpenUrlCrossRefPubMed
  3. 3.
  4. 4.
    F.-X. Lescure et al. Clinical and virological data of the first cases of COVID-19 in Europe: a case series. www.thelancet.com/infection Published online March 27, 2020 https://doi.org/10.1016/S1473-3099(20)30200-0
  5. 5.
  6. 6.↵
    Weinberger DM et al. Estimating the early death toll of COVID-19 in the United States. [Preprint.] MEDRXIV, 2020 Apr. https://doi.org/10.1101/2020.04.15.2006643
  7. 7.↵
    Nesteruk I. Long-term predictions for COVID-19 pandemic dynamics in Ukraine, Austria and Italy [Preprint.] MEDRXIV, 2020 Apr. DOI: 10.13140/RG.2.2.31170.53448
    OpenUrlCrossRef
  8. 8.↵
    Nesteruk I. SIR-simulation of Corona pandemic dynamics in Europe. [Preprint.] MEDRXIV, 2020 Apr. DOI: https://medrxiv.org/cgi/content/short/2020.04.22.20075135v1
  9. 9.↵
    Nesteruk I. Simulations and predictions of COVID-19 pandemic with the use of SIR model. Innov Biosyst Bioeng, 2020, vol. 4, no. 2, 110–121, doi: 10.20535/ibb.2020.4.2.204274. http://ibb.kpi.ua/article/view/204274
    OpenUrlCrossRef
  10. 10.
    Nesteruk I. Hidden periods, duration and final size of COVID-19 pandemic. Preprint. MedRxiv. May 10, 2020. https://www.medrxiv.org/content/what-unrefereed-preprintw https://medrxiv.org/cgi/content/short/2020.05.10.20097147v1
  11. 11.↵
    Nesteruk I. COVID19 pandemic dynamics. Springer Nature, 2021, DOI: 10.1007/978-981-33-6416-5
    OpenUrlCrossRef
  12. 12.↵
    Kermack WO, McKendrick AG. A Contribution to the mathematical theory of epidemics. J Royal Stat Soc Ser A. 1927;115:700–21.
    OpenUrl
  13. 13.↵
    Murray JD. Mathematical Biology I/II. New York: Springer; 2002.
  14. 14.↵
    Langemann D, Nesteruk I, Prestin J. Comparison of mathematical models for the dynamics of the Chernivtsi children disease. Mathematics in Computers and Simulation. 2016;123:68–79. DOI: 10.1016/j.matcom.2016.01.003
    OpenUrlCrossRef
  15. 15.↵
    Nesteruk I. Statistics based models for the dynamics of Chernivtsi children disease. Naukovi Visti NTUU KPI. 2017;5:26–34. DOI: 10.20535/1810-0546.2017.5.108577
    OpenUrlCrossRef
  16. 16.↵
    Nesteruk I. Statistics-based predictions of coronavirus epidemic spreading in mainland China. Innov Biosyst Bioeng. 2020; 4(1):13–18. DOI: 10.20535/ibb.2020.4.1.195074.
    OpenUrlCrossRef
  17. 17.↵
  18. 18.↵
  19. 19.↵
    COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). https://github.com/owid/covid-19-data/tree/master/public/data
  20. 20.↵
    Nesteruk, I. “Comparison of the coronavirus pandemic dynamics in Ukraine and neighboring countries” [Preprint.] ResearchGate. 2020 Mar. doi: 10.13140/RG.2.2.31170.53448
    OpenUrlCrossRef
  21. 21.
    Nesteruk, I., Kydybyn, I., Demelmair, G. Corona pandemic global stabilization? [Preprint.] ResearchGate. 2020 April. doi: 10.13140/RG.2.2.21570.32961 https://www.researchgate.net/publication/340917471_Corona_pandemic_global_stabilization
    OpenUrlCrossRef
  22. 22.↵
    Nesteruk, I., Kydybyn, I., Demelmair, G. GLOBAL STABILIZATION TRENDS OF COVID-19 PANDEMIC. KPI Science News, 2020, No. 2, pp. 55–62. DOI: 10.20535/kpi-sn.2020.2.205124
    OpenUrlCrossRef
  23. 23.↵
    Nesteruk I. Як довго українці сидітимуть на карантині? How long will the Ukrainians stay in quarantine? (in Ukrainian) [Preprint.] ResearchGate. 2020 Apr. doi: 10.13140/RG.2.2.15732.71046
    OpenUrlCrossRef
  24. 24.
    Nesteruk I. Динаміка COVID-19 епідемії в Україні та Києві після покращання тестування. COVID-19 epidemic dynamics in Ukraine and Kyiv after testing has improved (In Ukrainian). [Preprint.] ResearchGate. 2020 Apr. doi: 10.13140/RG.2.2.36705.86885
    OpenUrlCrossRef
  25. 25.↵
    Nesteruk I. Статистика пандемії COVID-19 в Україні та світі COVID-19 pandemic statistics in Ukraine and world. (In Ukrainian). ResearchGate. 2020 May doi:10.13140/RG.2.2.30999.39842 https://www.researchgate.net/publication/341542317_Statistika_pandemii_COVID-19_v_Ukraini_ta_sviti_COVID-19_pandemic_statistics_in_Ukraine_and_world
    OpenUrlCrossRef
  26. 26.↵
    Nesteruk I. Coronasummer in Ukraine and Austria. [Preprint.] ResearchGate. 2020 June. DOI: 10.13140/RG.2.2.32738.56002
    OpenUrlCrossRef
  27. 27.↵
    Nesteruk I. Waves of COVID-19 pandemic. Detection and SIR simulations. MedRxiv. 2020 Aug. doi: https://doi.org/10.1101/2020.08.03.20167098 https://www.medrxiv.org/content/10.1101/2020.08.03.20167098v1
  28. 28.
    Nesteruk I. Нові хвилі пандемії COVID-19 в Україні. New waves of COVID-19 pandemic in Ukraine. (In Ukrainian). [Preprint.] ResearchGate. 2020 Aug. DOI:10.13140/RG.2.2.26172.26244 https://www.researchgate.net/publication/343979510_Novi_hvili_pandemii_COVID-19_v_Ukraini_New_waves_of_COVID-19_pandemic_in_Ukraine
    OpenUrlCrossRef
  29. 29.↵
    Nesteruk I. COVID-19 pandemic dynamics in Ukraine after September 1, 2020. MedRxiv. Posted December 22, 2020.Doi: https://doi.org/10.1101/2020.12.21.20248627
  30. 30.↵
    Nesteruk I. Estimates of the COVID-19 pandemic dynamics in Ukraine based on two data sets. MedRxiv. Posted February 20, 2021. Doi: https://doi.org/10.1101/2021.02.18.21252000
  31. 31.↵
  32. 32.↵
    Draper NR, Smith H. Applied regression analysis. 3rd ed. John Wiley; 1998.
  33. 33.↵
    Gazzola M., Argentina M. & L. Mahadevan. Scaling macroscopic aquatic locomotion. Nature Physics volume 10, pages 758–761 (2014).
    OpenUrl
  34. 34.↵
    I. Nesteruk, “Maximal speed of underwater locomotion”, Innov Biosyst Bioeng, 2019, vol. 3, no. 3, pp. 152–167. Doi: https://doi.org/10.20535/ibb.2019.3.3.177976
    OpenUrl
  35. 35.↵
  36. 36.↵
  37. 37.↵
    Joseph T Wu, Kathy Leung, Gabriel M Leung.Nowcasting and Forecasting the Potential Domestic and International Spread of the 2019-nCoV Outbreak Originating in Wuhan, China: A Modelling Study. Lancet 2020 Jan 31. DOI: 10.1016/S0140-6736(20)30260-9
    OpenUrlCrossRefPubMed
  38. 38.
    Shi Zhao, Qianyin Lin, Jinjun Ran, Salihu S Musa, Guangpu Yang, Weiming Wang, Yijun Lou, Daozhou Gao, and others. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. International Journal of Infectious Diseases. Published online: January 30, 2020. DOI:https://doi.org/10.1016/j.ijid.2020.01.050
  39. 39.
    Byass, P. Eco-epidemiological assessment of the COVID-19 epidemic in China, January-Februry 2020. medRxiv 2020, doi:10.1101/2020.03.29.20046565.
    OpenUrlAbstract/FREE Full Text
  40. 40.
    Tang, B., Bragazzi, N. L., Li, Q., et al. “An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov).” Infectious disease modelling, vol. 5, pp. 248–255. 2020 Feb. 11. doi:10.1016/j.idm.2020.02.001.
    OpenUrlCrossRef
  41. 41.
    Ying Liu, Gayle AA, Wilder-Smith A, Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. Jurnal of Travel Medicine, Volume 27, Issue 2, March 2020, taaa021, https://doi.org/10.1093/jtm/taaa021
  42. 42.
    Kucharski AJ. et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. TheLancet Infectious Diseases (2020) Published:March 11, 2020DOI:https://doi.org/10.1016/S1473-3099(20)30144-4
  43. 43.
    Batista, M. “Estimation of the final size of the COVID-19 epidemic.” [Preprint.] medRxiv. 2020 Feb. 28. doi:10.1101/2020.02.16.20023606.
    OpenUrlAbstract/FREE Full Text
  44. 44.
    J. Dehning et al. Inferring COVID-19 spreading rates and potential change points for case number forecasts. Preprint, arxiv:2004.01105(2020).
  45. 45.
    Chen Y, Cheng J, Jiang Y, Liu K. A time delay dynamical model for outbreak of 2019-nCoV and the parameter identification. arxiv:2002.00418; 2020.
  46. 46.
    Peng L, Yang W, Zhang D, Zhuge C,Hong L. Epidemic analysis of COVID-19 in China by dynamical modeling. arxiv:2002.06563;2020.
  47. 47.
    Chang SL, Harding N, Zachreson C, Cliff OM, Prokopenko M. Modelling transmission and control of the COVID-19 pandemic in Australia. arxiv:2003.10218; 2020.
  48. 48.
    Maier BF, Brockmann D. Effective containment explains sub-exponential growth in confirmed cases of recent COVID-19 out break in mainland China. arxiv:2002.07572;2020.
  49. 49.
    Song PX, Wang L, Zhou Y, He J, Zhu B, Wang F, et al. An epidemiological forecast model and software assessing interventions on COVID-19 epidemic in China. MedRxiv. 2020;
  50. 50.
    Chinazzi M, Davis JT, Ajelli M, Gioannini C, Litvinova M, Merler S, et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020; 368(6489):395–400. https://doi.org/10.1126/science.aba9757PMID:32144116
    OpenUrlAbstract/FREE Full Text
  51. 51.
    Zhang Y,Jiang B,Yuan J, Tao Y. The impact of social distancing and epicenter lockdown on the COVID-19 epidemic in mainland China: A data-driven SEIQR model study. MedRxiv. 2020;
  52. 52.
    Noureddine Benlagha. Modeling the Declared New Cases of COVID-19 Trend Using Advanced Statistical Approaches. [Preprint.] ResearchGate. March 2020. DOI: 10.6084/m9.figshare.12052638
    OpenUrlCrossRef
  53. 53.
    Chang SL, Harding N, Zachreson C, Cliff OM, Prokopenko M. Modelling transmission and control of the COVID-19 pandemic in Australia. arxiv:2003.10218;2020.
  54. 54.
    Pongkaew Udomsamuthirun et al. The reproductive index from SEIR model of Covid-19 epidemic in Asean. [Preprint.] MEDRXIV, 2020 Apr. DOI: https://doi.org/10.1101/2020.04.24.20078287
  55. 55.
    Pereira IG et al. Forecasting Covid-19 Dynamics in Brazil: A Data Driven Approach. Int. J. Environ. Res. Public Health 2020, 17(14), 5115; https://doi.org/10.3390/ijerph17145115
    OpenUrl
  56. 56.
    Linka K., Peirlinck M., Kuhl E. The reproduction number of COVID-19 and its correlation with public health interventions. [Preprint.] MEDRXIV, 2020. DOI:10.1101/2020.05.01.20088047
    OpenUrlAbstract/FREE Full Text
  57. 57.
    Distante, C., Gadelha Pereira, I., Garcia Goncalves, L.M., Piscitelli, P., Miani, A. Forecasting Covid-19 Outbreak Progression in Italian Regions: A model based on neural network training from Chinese data. medRxiv 2020.
  58. 58.
    Hamzah, F., Binti, A., Lau, C., Nazri, H., Ligot, D.V., Lee, G., Tan, C.L. CoronaTracker: Worldwide COVID-19 Outbreak Data Analysis and Prediction. Bull. World Health Organ. 2020, 1, 32.
    OpenUrlCrossRef
  59. 59.
    Fanelli, D., Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761.
    OpenUrl
  60. 60.
    Webb, G.F., Magal, P., Liu, Z., Seydi, O. A model to predict COVID-19 epidemics with applications to South Korea, Italy, and Spain. medRxiv 2020.
  61. 61.
    Bastos, S.B., Cajueiro, D.O. Modeling and forecasting the early evolution of the Covid-19 pandemic in Brazil. arXiv 2020, arxiv:2003.14288.
  62. 62.
    Grant, A. Dynamics of COVID-19 epidemics: SEIR models underestimate peak infection rates and overestimate epidemic duration. medRxiv 2020.
  63. 63.
    Loli Piccolomiini, E., Zama, F. Monitoring Italian COVID-19 spread by an adaptive SEIRD model. medRxiv 2020.
  64. 64.
    Baerwolff, G.K. A Contribution to the Mathematical Modeling of the Corona/COVID-19 Pandemic. medRxiv 2020.
  65. 65.
    Distante, C., Piscitelli, P., Miani, A. Covid-19 Outbreak Progression in Italian Regions: Approaching the Peak by the End of March in Northern Italy and First Week of April in Southern Italy. Int. J. Environ. Res. Public Health 2020, 17, 3025.
    OpenUrlPubMed
  66. 66.
    Vrugt, M., Bickmann, J., Wittkowski, R. Effects of social distancing and isolation on epidemic spreading: A dynamical density functional theory model. arXiv 2020, arxiv:2003.13967.
  67. 67.
    Yang, Z., Zeng, Z., Wang, K., Wong, S.S., Liang, W., Zanin, M., Liu, P., Cao, X., Gao, Z., Mai, Z., et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165.
    OpenUrlCrossRef
  68. 68.
    Roda, W.C., Varughese, M.B., Han, D., Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281.
    OpenUrl
  69. 69.
    Otunuga, O.M., Ogunsolu, M.O. Qualitative analysis of a stochastic SEITR epidemic model with multiple stages of infection and treatment. Infect. Dis. Model. 2020, 5, 61–90.
    OpenUrl
  70. 70.
    K Chatterjee et al. Healthcare impact of COVID-19 epidemic in India: A stochastic mathematical model. Medical Journal Armed Forces India. Volume 76, Issue 2, April 2020, Pages 147-155
    OpenUrl
  71. 71.
    I Ciufolini, A Paolozzi. Mathematical prediction of the time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur. Phys. J. Plus (2020) 135: 355 https://doi.org/10.1140/epjp/s13360-020-00383-y
    OpenUrlCrossRef
  72. 72.
    S Annas et al. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos, Solitons & Fractals Volume 139, October 2020, 110072 https://doi.org/10.1016/j.chaos.2020.110072
    OpenUrl
  73. 73.
    RP Yadav, R Verma A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos, Solitons & Fractals. Volume 140, November 2020, 110124 https://doi.org/10.1016/j.chaos.2020.110124
    OpenUrl
  74. 74.
    KY Ng, MM Gui. COVID-19: Development of a robust mathematical model and simulation package with consideration for ageing population and time delay for control action and resusceptibility. Physica D: Nonlinear Phenomena.Volume 411, October 2020, 132599 https://doi.org/10.1016/j.physd.2020.132599Getrightsandcontent
    OpenUrl
  75. 75.
    B. Ivorra, M.R. Ferrández, M. Vela-Pérez, A.M. Ramos. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Communications in Nonlinear Science and Numerical Simulation, Volume 88, September 2020, 105303, https://doi.org/10.1016/j.cnsns.2020.105303
    OpenUrl
  76. 76.
    Nguyen HuyTuan, Hakimeh Mohammadi, Shahram Rezapour. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos, Solitons & Fractals. 2020, 110107. https://doi.org/10.1016/j.chaos.2020.110107
  77. 77.
    Musalula Sinkala, Panji Nkhoma, Mildred Zulu, Doris Kafita, Rabecca Tembo, Victor Daka. The COVID-19 Pandemic in Africa: Predictions using the SIR Model. medRxiv 2020.06.01.20118893; doi: https://doi.org/10.1101/2020.06.01.2011889
  78. 78.
    Komi Agbokou1, Kossi Gneyou1, Kokou Tcharie. Investigation on the temporal evolution of the covid’19pandemic: prediction for Togo. Open Jornal of mathematical sciencies. 2020, 4, 273–279; doi:10.30538/oms2020.0118 https://pisrt.org/psr-press/journals/oms
    OpenUrlCrossRef
  79. 79.
    Gergő Pintér, Imre Felde, Amir Mosavi, Richard Gloaguen. COVID-19 Pandemic Prediction for Hungary; A Hybrid Machine Learning Approach. Mathematics 2020, 8, 890; doi:10.3390/math8060890www.mdpi.com/journal/mathematics
    OpenUrlCrossRef
  80. 80.
    Cody Carroll et al. Time Dynamics of COVID-19. medRxiv 2020.05.21.20109405; doi: https://doi.org/10.1101/2020.05.21.2010940
  81. 81.
    Khaled M Furati, Ibrahim O. Sarumi, Abdul Q.M. Khaliq. Memory-Dependent Model for the Dynamics of COVID-19 Pandemic. medRxiv 2020.06.26.20141242; doi: https://doi.org/10.1101/2020.06.26.20141242
  82. 82.
    Jurgen Bosch, Austin Wilson, Karthik O’Neil, Pater A Zimmerman. COVID-19 Predict-Predicting Pandemic Trends. medRxiv 2020.09.09.20191593; doi: https://doi.org/10.1101/2020.09.09.20191593
  83. 83.
    Ali Asad, Siddharth Srivastava, Mahendra K. Verma. Evolution of COVID-19 Pandemic in India. medRxiv 2020.07.01.20143925; doi: https://doi.org/10.1101/2020.07.01.20143925
  84. 84.
    Nawel Aries, Houdayfa Ounis. Mathematical Modeling of COVID-19 Pandemic in the African Continent. medRxiv 2020.10.10.20210427; doi: https://doi.org/10.1101/2020.10.10.20210427
  85. 85.
    Felix Guenther, Andreas Bender, Katharina Katz, Helmut Kuechenhoff, Michael Hoehle. Nowcasting the COVID-19 Pandemic in Bavaria. medRxiv 2020.06.26.20140210; doi: https://doi.org/10.1101/2020.06.26.20140210
  86. 86.
    Wan Yang, Jaimie Shaff, Jeffrey Shaman. COVID-19 Transmission Dynamics and Effectiveness of Public Health Interventions in New York City during the 2020 Spring Pandemic Wave. medRxiv 2020.09.08.20190710; doi: https://doi.org/10.1101/2020.09.08.20190710
  87. 87.
    Ronald Dickman. A SEIR-like model with a time-dependent contagion factor describes the dynamics of the Covid-19 pandemic. medRxiv 2020.08.06.20169557; doi: https://doi.org/10.1101/2020.08.06.20169557
  88. 88.
    Lakshmi Rani Kundu, Most. Zannatul Ferdous, Ummay Soumayia Islam, Marjia Sultana. Forecasting the spread of COVID-19 pandemic in Bangladesh using ARIMA model. medRxiv 2020.10.22.20217414; doi: https://doi.org/10.1101/2020.10.22.20217414
  89. 89.
    Diego Carvalho, Rafael Barbastefano, Dayse Pastore, Maria Clara Lippi. A novel predictive mathematical model for COVID-19 pandemic with quarantine, contagion dynamics, and environmentally mediated transmission. medRxiv 2020.07.27.20163063; doi: https://doi.org/10.1101/2020.07.27.20163063
  90. 90.
    Md. Haider Ali Biswas, M. S. Khatun, A. K. Paul, M. R. Khatun, M. A. Islam, S. A. Samad, U. Ghosh. Modeling the Effective Control Strategy for Transmission Dynamics of Global Pandemic COVID-19. medRxiv 2020.04.22.20076158; doi: https://doi.org/10.1101/2020.04.22.20076158
  91. 91.
    Elinor Aviv-Sharon, Asaph Aharoni. Forecasting COVID-19 pandemic Severity in Asia. medRxiv 2020.05.15.20102640; doi: https://doi.org/10.1101/2020.05.15.20102640
  92. 92.
    Nayana Bannur, Harsh Maheshwari, Sansiddh Jain, Shreyas Shetty, Srujana Merugu, Alpan Raval. Adaptive COVID-19 Forecasting via Bayesian Optimization. medRxiv 2020.10.19.20215293;doi: https://doi.org/10.1101/2020.10.19.2021529
  93. 93.
    Sewanou H. Honfo, Beaugard H. Taboe, Romain Glele Kakai. Modeling COVID-19 dynamics in the sixteen West African countries. medRxiv 2020.09.04.20188532; doi: https://doi.org/10.1101/2020.09.04.20188532
  94. 94.
    Piotr T. Chruściel, Sebastian J. Szybka. Universal properties of the dynamics of the Covid-19 pandemics. medRxiv 2020.08.24.20181214; doi: https://doi.org/10.1101/2020.08.24.20181214
  95. 95.
    BRAHMATHEJA REDDY MALI REDDY, ANUJ SINGH, PRADEEP SRIVASTAVA. COVID-19 TRANSMISSION DYNAMICS IN INDIA WITH EXTENDED SEIR MODEL. medRxiv 2020.08.15.20175703; doi: https://doi.org/10.1101/2020.08.15.20175703
  96. 96.
    Jianping Huang, Xiaoyue Liu, Li Zhang, Kehu Yang, Yaolong Chen, Zhongwei Huang, Chuwei Liu, Xinbo Lian, Danfeng Wang. The amplified second outbreaks of global COVID-19 pandemic. medRxiv 2020.07.15.20154161; doi: https://doi.org/10.1101/2020.07.15.2015416
  97. 97.
    Gyan Bhanot, Charles DeLisi. Analysis of Covid-19 Data for Eight European Countries and the United Kingdom Using a Simplified SIR Model.medRxiv 2020.05.26.20114058; doi: https://doi.org/10.1101/2020.05.26.20114058
  98. 98.
    Mahmoud A. Ibrahim, Amenah Al-Najafi. Modeling, Control, and Prediction of the Spread of COVID-19 Using Compartmental, Logistic, and Gauss Models: A Case Study in Iraq and Egypt. Processes 2020,8, 1400; doi:10.3390/pr8111400
    OpenUrlCrossRef
  99. 99.
    Gaetano Perone. Comparison of ARIMA, ETS, NNAR and hybrid models to forecast the second wave of COVID-19 hospitalizations in Italy (HEDG-WP 20/18, University of York). Preprint. http://www.york.ac.uk/economics/postgrad/herc/hedg/wps/
  100. 100.
    Átila Madureira Bueno, Cristiane M. Batistela, Diego Paolo Ferruzzo Correa, J.R.C. Piqueira. SIRSi compartmental model for COVID-19 pandemic with immunity loss. Chaos Solitons & Fractals, Oct 2020. DOI: 10.1016/j.chaos.2020.110388
    OpenUrlCrossRef
  101. 101.
    Ahmed E. Fahmya, Mohammed M. El-desoukya, Ahmed S.A. Mohamed. Epidemic Analysis of COVID-19 in Egypt, Qatar and Saudi Arabia using the Generalized SEIR Model. MedRxiv. Posted August 22, 2020. Doi: https://doi.org/10.1101/2020.08.19.20178129
  102. 102.↵
    Ryad Ghanam, Edward L. Boone, Abdel-Salam G. Abdel-Salam. SEIRD MODEL FOR QATAR COVID-19 OUTBREAK: A CASE STUDY. Posted 26 May 2020. arxiv:2005.12777v1
Back to top
Posted March 27, 2021.
Download PDF
Data/Code
Email
Visible and real sizes of the COVID-19 pandemic in Ukraine
Igor Nesteruk
medRxiv 2021.03.19.21253938; doi: https://doi.org/10.1101/2021.03.19.21253938
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area