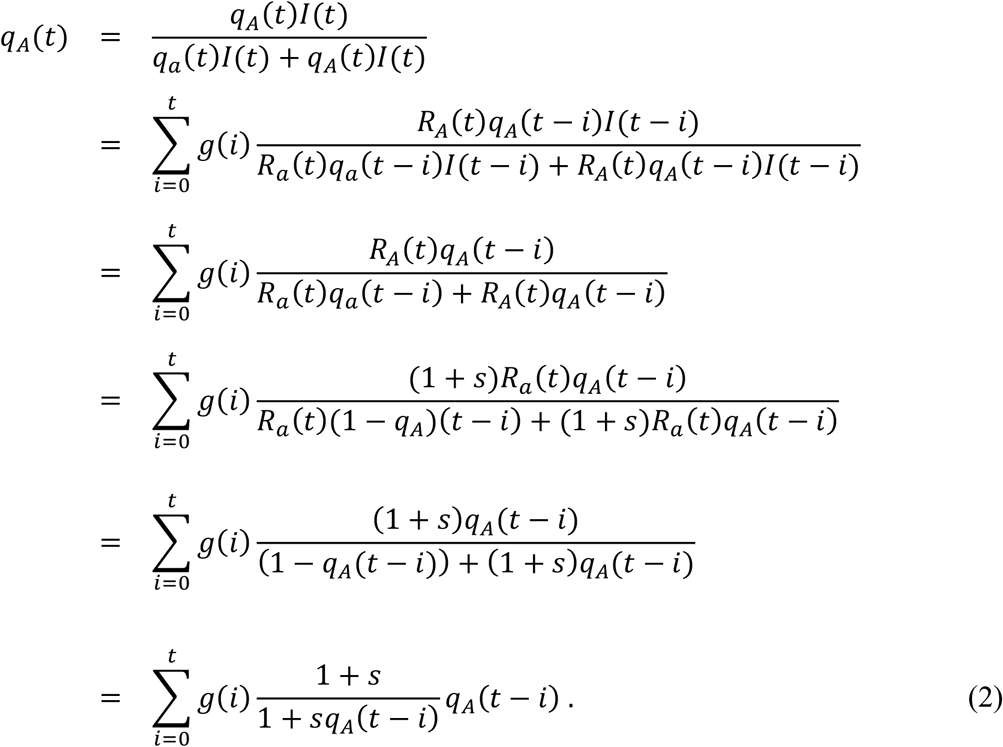Abstract
The B.1.1.7 strain, a variant strain of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), is thought to have higher transmissibility than previously circulating strains in England. The fraction of the B.1.1.7 strain among SARS-CoV-2 viruses in England have grown rapidly. In this paper, we propose a method to estimate the selective advantage of a mutant strain over previously circulating strains using the time course of the fraction of B.1.1.7 strains. Based on Wallinga-Teunis’s method to estimate the instantaneous reproduction numbers, our method allows the reproduction number to change during the target period of analysis. Our approach is also based on the Maynard Smith’s model of allele frequencies in adaptive evolution, which assumes that the selective advantage of a mutant strain over previously circulating strains is constant over time. Applying this method to the sequence data in England using serial intervals of COVID-19, we found that the transmissibility of the B.1.1.7 strain is 40% (with a 95% confidence interval (CI) from 40% to 41%) higher than previously circulating strains in England. The date of the emergence of B.1.1.7 strains in England was estimated to be September 20, 2020 with its 95% CI from September 11 to September 20, 2020. The result indicated that the control measure against the B.1.1.7 strain needs to be strengthened by 40% from that against previously circulating strains. To get the same control effect, contact rates between individuals need to be restricted to 0.71 of the contact rates that have been achieved form the control measure taken for previously circulating strains.
Introduction
Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the causative agent of COVID-19, has been rapidly evolving since its emergence in 2019. In December 2020, the Public Health England detected a new cluster of SARS-CoV-2 viruses phylogenetically distinct from the other strains circulating in the United Kingdom (Chand et al., 2020). These viruses belong to the lineage B.1.1.7 according to the PANGO nomenclature (Andrew. Rambaut et al., 2020) and the World Health Organization (WHO) designated them as Variant of Concern, year 2020, month 12, variant 01 (VOC 202012/01) (World Health Organization, 2020).
The B.1.1.7 strain was first detected in England in September 2020, and the numbers of infections with this strain increased in October and November in 2020 (Chand et al., 2020). By February 2021, B.1.1.7 strain occupied 95% of the SARS-CoV-2 circulating in England (Davies et al., 2021).
Several studies have compared the transmissibility of the B.1.1.7 strain to that of previously circulating strains. Davies et al. estimated that the reproduction number of the B.1.1.7 strain is 43–90% (with a 95% credible interval of 38–130%) higher than preexisting strains using data from England (Davies et al., 2021). However, different models resulted in different ranges of estimates in their multiplicative increase in reproduction number (R). Grabowski et al. estimated a 83–118% increase with a confidence interval of 71–140% compared to previously circulating strains in England (Grabowski et al., 2021). Volz et al. estimated 40–75% increase in R using data from England (Volz et al., 2021). Their methods use linear regression of log odds ratio between B.1.1.7 strain and previously circulating strains and estimate increase of transmissibility under assumption that R is constant over time during the target period of analysis. Washington et al. estimated a 35–45% increase using data from the United States of America using Volz’s method (Washington et al., 2021). Chen et al. estimated 49–65% increase in reproduction number using data from Switzerland also under the constant R assumption (Chen et al., 2021). Due to the high transmissibility the B.1.1.7 strain, strong control measure such as lockdown was taken when the strain was introduced (Davies et al., 2021). Thus, the constant R assumption is questionable when analyzing the increase in the reproduction number of B.1.1.7 compared to that of previously circulating strains.
In this paper, we propose a method to estimate the selective advantage of a mutant strain over previously circulating strains. Based on Wallinga-Teunis’s method to estimate the instantaneous reproduction numbers (Wallinga & Teunis, 2004), our method allows the reproduction number to change during the target period of analysis. Our approach is also based on the Maynard Smith’s model of allele frequencies in adaptive evolution, which assumes that the selective advantage of a mutant strain over previously circulating strains is constant over time (Maynard Smith & Haigh, 1974). Appling the developed method to the sequence data in England using the serial interval distribution of COVID-19 estimated by Nishiura et al. (Nishiura et al., 2020), we estimate the increase in the instantaneous reproduction number of B.1.1.7 strains compare to that of previously circulating strains. Based on the estimate, we discuss its implication to control measures for COVID-19.
Materials and Methods
Sequence data
Nucleotide sequences of SARS-CoV-2 viruses was downloaded from GISAID EpiCoV database (Shu & McCauley, 2017) on March 1, 2021. Nucleotide sequences that determined from viruses detected in England were selected and aligned to the reference amino acid sequence of S protein of SARS-CoV-2 virus (YP_009724390) using DIAMOND (Buchfink et al., 2015). The aligned nucleotide sequences were translated into amino acid sequences, then were aligned with the reference amino acid sequence of S protein using MAFFT (Katoh et al., 2002). Amino acid sequences having either an ambiguous amino acid or more than ten gaps were excluded from the rest of analyses. Table 1 shows amino acids on S protein of characterizing B.1.1.7 strain, retrieved from the PANGO database (Andrew. Rambaut et al., 2020).
We divided amino acid sequences into three groups based on amino acids shown in Table 1. The first group is sequences having all of B.1.1.7-defining amino acid substitutions in Table 1. We call a virus in this group a “B.1.1.7 strain”. The second group are sequences which have none of the B.1.1.7-defining substitutions. We call a virus in the this group a “non-B.1.1.7 strain”. The third group are sequences which have at least one but incomplete set of the B.1.1.7-defining amino acid substitutions. We called a strain in the third group a “B.1.1.7-like strain”. Table 2 shows the number of sequences categorized into each group. We used the number of B.1.1.7 strains and non-B.1.1.7 strains for the rest of the analyses. B.1.1.7-like strains were excluded from the analyses, since we do not know whether they had the same transmissibility as B.1.1.7 strains or not. Figure 1 shows the daily numbers of GISAID sequences of B.1.1.7 strains, non-B.1.1.7 strains and B.1.1.7-like strains detected in England from September 1, 2020 to February 19, 2021. These numbers are provided in Supplementary Table 1.
Serial interval distribution
The method we propose in this paper uses discrete distributions of serial intervals. Function g(i) gives the probability that the onset day of a secondary infection is at i days after the onset day of its primary case. We obtained the values of g(i) by discretizing the lognormal distribution of serial intervals of COVID-19 estimated by Nishiura et al. (Nishiura et al., 2020). Thus, the probability mass function of serial intervals is given by
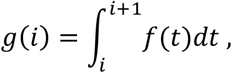where f(t) is the probability density function of a lognormal distribution with a mean of 4.7 days and a standard deviation of 2.9 days.
Model of Advantageous Selection
Consider we have a large population of viruses consisting of strains of two genotypes A and a, of which fraction in the viral population at a calendar date t are qA(t) and qa(t), respectively. Suppose also that genotype A is mutant of a that emerges at time t0.
We assume that a virus of genotype A generates 1 + s times as many secondary transmissions as those of genotype a. Then, s can be considered as the coefficient of selective advantage in adaptive evolution. As described by Maynard Smith and Haigh (1974), the fraction of viruses of allele A after the n transmissions, qn, satisfies
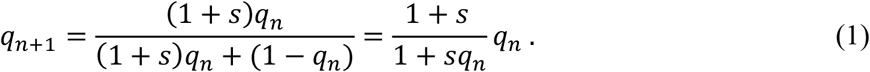
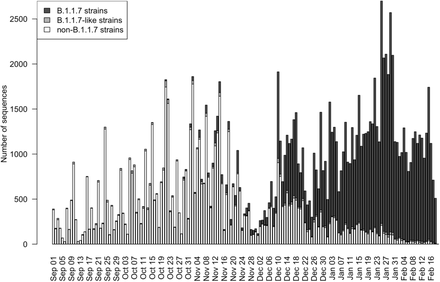
Let g(i) be a discrete distribution of serial intervals defined in the previous subsection. Since the expected fraction of allele A in the population at calendar time t can be represented as s and qA(t − i) for 0 ≤ i ≤ t with a probability of g(i), the value of qA(t) can be represented as follows.
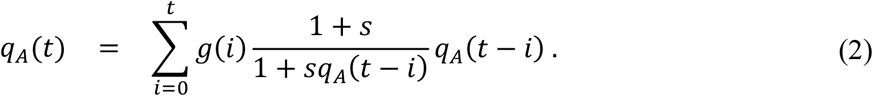
See Appendix for the relationship between Equation (2) and instantaneous reproduction numbers proposed by Wallinga and Teunis (Wallinga & Teunis, 2004). Assuming g(0) = 0, we can approximate the formula.
Likelihood Function
Let n(t) be the number of sequences of either genotype A or a observed at calendar date t. Let d1, …, dk be calendar dates such that n(di) > 0 for 1 ≤ j ≤ k. Suppose that we have nA(dj) samples of genotype A at calendar date dj. Since genotype A emerged at time t0, qA(dj) = 0 and qa(dj) = 1 for dj < t0. Let q0 be initial frequency of genotype A, i.e., q0 = qA(t0). Then the following equation gives the likelihood function of s, t0, and q0 for observing nA(dj) samples of viruses of genotype A at calendar date dj.
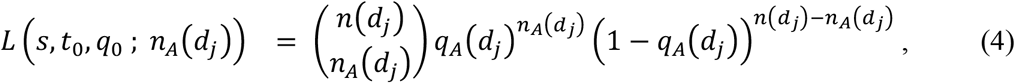for 1 ≤ j ≤ k. The likelihood function of s, t0, and q0 for observing nA(d1), …, nA(dk) sequences of genotype A at calendar dates d1, …, dk is given by the following formula.
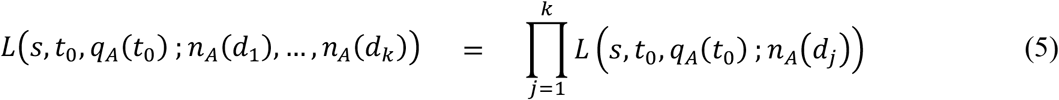
Parameter estimation from sequence data
The B.1.1.7 strain was first detected in England on September 20, 2020. We assume that t0 is this day or someday before this day. Parameters s, t0, and q0 were estimated by maximizing likelihood of observations on September 1, 2020 and later on. B.1.1.7 strains, viruses having complete subset of B.1.1.7-difining substitutions on its S protein were considered as genotype A. The non-B.1.1.7 strains, viruses having none of B.1.1.7-defining substitutions were considered to be genotype a. The B.1.1.7-liike strains, viruses having an incomplete set of B.1.1.7 substitutions on the S protein, were excluded from the analysis. Parameters of s, t0, and q0 were estimated by maximizing log likelihood defined in Equation (5). The 95% confidence intervals of parameters were estimated by profile likelihood (Pawitan, 2013). The optimization of likelihood function was done by the nloptr package in R (Johnson; Rowan, 1990).
Results
The selective advantage of B.1.1.7 strains over non-B.1.1.7 strains, s, was estimated to be 0.40 with its 95% confidence intervals from 0.40 to 0.41 (Table 2). The date of emergence of B.1.1.7 strains in England, t0, was estimated to be September 20, 2020 with its 95% confidence interval from September 11, 2020 to September 20, 2020. The initial fraction of B.1.1.7 among non-B.1.1.7 and B.1.1.7 strains at the emergence in England, q0, was estimated to be 0.0030 with its 95% confidence intervals from 0.0014 to 0.0031.
Figure 1 shows the time course of the fraction of B.1.1.7 strains among all strains except B.1.1.7-like strains detected in the England from September 1, 2020 to February 19, 2021. White circles indicate daily fractions of B.1.1.7 strains among all strains except B.1.1.7-like strains. Solid line indicates the time course of fraction of B.1.1.7 strains calculated using parameters estimated from the data. Dashed lines indicate its lower and upper bound of its 95% CI.
Discussion
In this paper, the selective advantage of the B.1.1.7 strain in England over non-B.1.1.7 strains was estimated to be 0.40 with a 95% CI from 0.40 to 0.41. The date of emergence of B.1.1.7 strains in England was estimated to be September 20, 2020 with its 95% confidence interval from September 11, 2020 to September 20, 2020. The initial fraction of B.1.1.7 among all sequences except B.1.1.7-like strains at the time of emergence in England was estimated to be 0.0030 with its 95% confidence intervals from 0.0014 to 0.0031.
Our estimation method is based on the principle that the expected fraction of a mutant strain among all strains can be determined from those in previous generation using the serial interval distribution of infections. The method is related to Wallinga-Teunis’s method for estimating the instantaneous reproduction number, and thus it allows reproduction numbers of strains to change during the target period of analysis. Instead, our method assumes that the selective advantage of a mutant strain over previously circulating strains is constant over time, which is based on Maynard Smith’s model of allele frequencies in adaptive evolution.
The estimated selective advantage of 0.40 indicates that the instantaneous reproduction number of the B.1.1.7 strain is 40% higher than that of previously circulating strains in England. This means that the control measures for the B.1.1.7 strain needs to be strengthened by 40% compared to that for the previously circulating strains. To get the same control effect, contact rates between individuals needs to be restricted below 1/1.40 = 0.71 of the contact rates to achieve the same control measure for the previously circulating strains.
Our method relies on the serial interval distribution, and thus the results may change depending on serial interval distribution used in the analysis. In this paper, we used the serial interval distribution estimated by Nishiura et al. (Nishiura et al., 2020). The distribution is a lognormal distribution with a mean serial interval of 4.7 days with a standard deviation of 2.9 days. Several groups have estimated the serial intervals of SARS-CoV-2 using different datasets. Some variations are observed among these estimated values (Rai et al., 2021). Volz et al. (Volz et al., 2021) assumes a fixed serial interval of 6.5 days based on results by Bi et al. (Bi et al., 2020). However, Ali et al. have reported that the serial interval estimated using data from China during before January 22, 2020 was longer than estimates after January 22, 2020 (Ali et al., 2020). The serial interval estimated by Bi et al. contains data before January 22, 2020 and there might be some possibility that the estimated serial interval does not reflect the current situation. This is the reason why we did not use serial interval estimated by Bi et al.
As of March 17, 2021, the B.1.1.7 strain has now been observed in 93 countries (A. Rambaut et al., 2020). The selective advantage of the B.1.1.7 strains over previously circulating strains in other countries remains to be our future work. Variant strains originated in Brazil and South Africa also show higher transmissibility than previously circulating strains (World Health Organization, 2021). There is an urgent need to estimate the selective advantage of these strains over previously circulating strains.
Data Availability
Supplementary Table S1 contains the dataset used in the analysis.
Conflict of Interest
We declare that there is no conflict of interest.
Acknowledgement
We gratefully acknowledge the laboratories responsible for obtaining the specimens and the laboratories where genetic sequence data were generated and shared via the GISAID Initiative, on which this research is based. This work was supported by CREST (grant number JPMJCR1413) from Japan Science and Technology Agency (http://www.jst.go.jp/), and the World-leading Innovative and Smart Education (WISE) Program (1801) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan (http://www.mext.go.jp/). The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Appendix
Derivation of Equation (2)
Let I(t) be the number of infections by viruses of either genotype A or a at calendar time t and g(i) be the probability mass function of serial intervals. Suppose that the instantaneous reproduction number of genotypes A and a at calendar time t are RA(t) and Ra(t). The following equations give the discrete version of Wallinga-Teunis’s instantaneous reproduction numbers of infections by genotype A and a at time t.
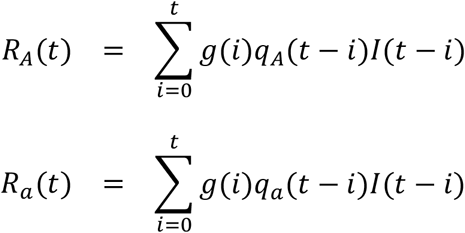
Next suppose that RA(t) = (1 + s)Ra(t) for every calendar time t, then the expected value of qA(t) can be calculated as follows.
References
