Abstract
Infectious diseases, like COVID-19, pose serious challenges to university campuses, and they typically adopt closure as a non-pharmaceutical intervention to control spread early and ensure a gradual return to normalcy. These policies, like remote instruction (RI), reduce potential contact but also have broad side-effects on campus by hampering local economy, students’ learning outcomes, and community wellbeing. In this paper, we demonstrate that university policymakers can mitigate these tradeoffs by leveraging anonymized data from their WiFi infrastructure to learn community mobility (WiMob) and in turn explore more granular policies like localized closures (LC). WiMob can construct contact networks that capture behavior in a variety of spaces, highlighting new potential transmission pathways and temporal variation in contact behavior. Additionally, WiMob enables us to design LC policies that close super-spreader locations on campus. On simulating disease spread with contact networks from WiMob, we find that LC maintains the same reduction in cumulative infections as RI while showing greater reduction in peak infections and internal transmission. Moreover, LC reduces campus burden by closing fewer locations, forcing fewer students into completely online schedules, and requiring no additional isolation. WiMob can empower universities to conceive and assess a variety of closure policies to prevent future outbreaks.
Introduction
University campuses are often hotspots for infectious disease outbreaks and hence are usually targeted for interventions. In the wake of the Coronavirus Disease (COVID-19) [41], the U.S. alone witnessed more than half a million cases at universities [54], and colleges are still left with decisions for operations in Fall 2021 [34, 44]. Controlling the disease at universities can be pivotal to securing the surrounding environment [5]. To reduce on-campus infections and the likelihood of superspreading events, a recommended form of non-pharmaceutical intervention (NPI) is partial closure of the campus [21]. During COVID-19, advancement in technology equips universities to continue operations by adopting a form of campus closure that relies on remote instruction (RI) [39]. As a consequence, the campus community has fewer opportunities to visit spaces to congregate and risk transmission, such as classrooms [1, 3]. One common approach campuses consider to design RI policies is to use enrollment data (En) to offer large classes online while offering other classes in person [7, 59]. In fact, during COVID-19, 44% colleges and universities in the U.S., primarily offered instruction online [52]. However, these policies can still have broad, negative, and indiscriminate impact on the community by forcing students into completely remote course schedules. Such policies can have adverse effect on learning outcomes [16], where students can lose close to 7 months of education [2]. Additionally, RI can disincentivize students to stay on campus and thus, incur losses in auxiliary revenue (e.g., boarding, parking, dining, etc.) [23, 15], with universities standing to lose up to $50 million because of unused services [63]. Even the local population unaffiliated with the university takes sustains losses to business due to university closures [28, 58]. Furthermore, with socioeconomic disparities and heterogeneous household contexts, the demands of remote instruction can lead to added anxiety and stress among students [11, 61]. Indeed, while campus closures have been deployed for prior epidemics as well, like influenza [9, 20], these policies have always been contentious because of significant disruption to educational and commercial activity, and social wellbeing [62]. Relying on RI, university campuses struggle to balance community health with the demands of learning, economy, and broad wellbeing [46]. Instead, there is a need for a more versatile approach to design closure policies that empowers policymakers to accurately assess impact of closure interventions and model more data-driven targeted intervention strategies.
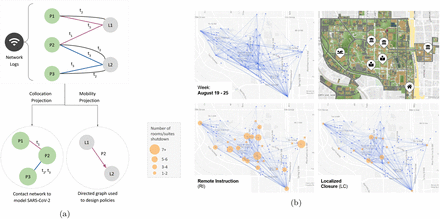
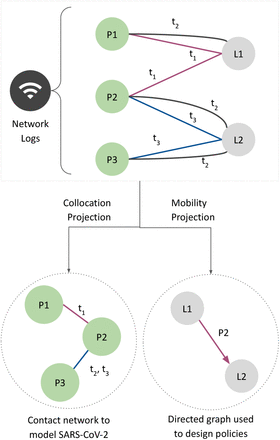
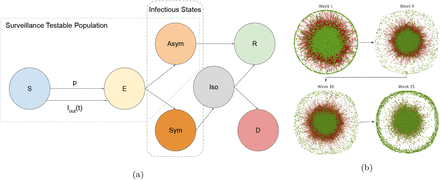
This paper showcases a new approach to conceive closure policies on campus by leveraging data in their existing WiFi infrastructure. Our methodology, WiMob, involves constructing anonymized mobility networks of campus (Figure 1a), which helps determine extended periods of collocation — or “proximate contact” [27]— between individuals to describe contact networks on campus. Particularly, WiMob enables a more expressive toolkit for university policymakers that represents contact longitudinally and allows them to assess closure at the granularity of a room, suite, or hall. Thus, it lends to the design of targeted inter-ventions that focus on localized closures (LC). We demonstrate the utility of WiMob with data collected over two years, of approximately 40, 000 anonymous occupants and visitors of the Georgia Institute of Technology (GT), a large urban campus in the U.S. — including about 16, 000 undergraduate students, 9, 000 graduate students, and 7, 600 staff members. In general, on comparing WiMob to En as an approach to model contact, we find that WiMob captures contact behavior at a community scale for a variety of campus spaces, describes temporal variations in contact, and provides a better estimate of local context by being aware of occupancy and the non-student population. Leveraging WiMob also reveals that En overestimates the impact of RI on reducing contact on campus. Hence, we propose a less burdensome alternative to RI, by deriving more targeted LC policies based on WiMob (Figure 1) (indeed En is too coarse-grained for designing targeted LC policies).
Anonymized WiFi network logs help model mobility on campus (WiMob) and target spaces for localized closures (LC) (a) WiFi network logs reflect timestamps when people’s devices associate with different access points (APs) on campus. WiMob mines these logs to characterize mobility as a bipartite graph that describes people (e.g., P1, P2) visiting locations (e.g., L1, L2) on campus during different times (e.g., t1, t2). Since people’s devices can proxy their presence, we estimate collocation (e.g., P1 and P2 were collocated at L1 at t1), and movement (P2 dwelled at L1 and then at L2). The collocation graph forms the basis of the contact structure for our ABM. (b) WiMob highlights mobility behavior to evaluate and inform policy. (b)–top-left: Mobility on campus between the top 100 most frequented locations on the GT campus in the Fall semester of 2019. Edges only connect points of significant dwelling and thus do not represent pedestrian routes. (b)–top-right: For reference, we annotate one large on-campus housing facility (south-east), the recreation center (west), two learning commons (center), and three highly frequented academic buildings. Some of the highest centrality locations are in these buildings. (b)–bottom-left: RI is a form of broad closure which affects a large number of students and locations.(b)–bottom-right: By contrast, we propose to use WiMob to parsimoniously identify a small set of spreader locations within buildings and design LC policies. With these policies, we aim to provide equal or better control on the disease spread, and yet minimize the burden on campus compared to RI.
We further exhibit that LC presents better disease control outcomes than RI by constructing and simulating an agent-based model (ABM) over the WiMob contact networks, calibrated with GT on-campus COVID-19 cases from the Fall semester of 2020 [25] and infection rates from Fulton County [40]. To compare the effect of interventions, we describe a counterfactual semester that is unaltered by other policy–induced behaviors of 2020 by leveraging WiFi data from Fall 2019 to determine the contact structure of the simulation. This model helps assess the effectiveness of closure NPIs (Figure 1b) under various behavioral scenarios. We find LC is comparable to RI in controlling total infections but more effective at reducing the peak infections and internal transmission. Additionally, LC targets fewer locations, forces fewer students into fully online schedules, and does not isolate any more people than RI – illustrating that WiMob can help universities devise highly-specific closure policies, like LC, which can contain disease spread and mitigate campus disruption in comparison to RI policies.
Our methodology also promises other advantages. Mobility generally has been used to dynamically model disease spread of influenza [47], rubella [60] and COVID-19 [3, 45]. For the latter, various studies show the effectiveness of mobility restrictions at a regional–, or city–level [66, 10, 6, 37, 30]. Previous studies that use mobility information to model disease spread and interventions typically rely on cell tower localization or aggregating GPS information from mobile phones. Neither of these data sources is easy to access for university campuses. In the past, studies to infer campus mobility have relied on accessing user devices with specialized data logging applications [12, 17, 49], but these approaches are typically constrained for disease modeling because they require mass adoption to represent the entire community and continuous maintenance of software is needed to capture longitudinal behavior changes. In contrast, this study repurposes already existing managed WiFi networks to model mobility, which provides room level granularity for mobility [18, 57, 13, 55] and consequently indicates proximate contact [27]. Much like En, universities internally archive such data over a long term for other purposes and do not need to install any additional surveillance infrastructure to access it. With the appropriate privacy considerations, a university can obtain this data at a low cost, continuously and unobtrusively.
The possibility of pandemic still looms large in the future [32, 24]. As campuses prepare for the upcoming Fall semester and unforeseen contagious diseases of tomorrow, WiMob presents an attractive and practical method to inform better public health policies.
Results
We present two sets of analyses in our work. The first set contrasts structural characteristics of contact networks described by WiMob with current practices that use En. In the next set, we use WiMob to model both RI and LC interventions and analyze their differences in terms of dynamic disease-control outcomes and burdens to campus.
WiMob provides local, holistic and dynamic structural insights for contact networks on campus
Studies on RI policies tend to assume that contact in universities is largely informed by En— transcripts showing which courses a student is registered for. En can provide structural in-sights on density of connections and disease transmission paths to inform modeling disease simulations [26]. However, such static data can overestimate attendance and ignore overlap between courses (via instructors) and organic interactions outside classes (e.g., waiting areas, dining, parties, and extra-curricular activities). Therefore, using En can overemphasize the disease-mitigating structural changes to the network by RI interventions. By contrast, WiMob is more grounded in community behavior as it captures multiple scheduled and serendipitous contact situations dynamically over the semester. We compare the features of contact networks constructed with WiMob, against networks constructed with En using data from GT for Fall semester of 2019 (August 19 – December 14), which is before any COVID-19 reported cases in the U.S. En approximates contact based on students enrolling for classes that could potentially collocate them in the same room during lectures. WiMob infers contact when any two individuals actually collocate near the same WiFi access point [13, 55] for extended period (see explanation in SI WiFi Mobility). We find that WiMob renders new insight into contact on campus that is invisible to the En methodology.
WiMob characterizes temporal variation in proximity
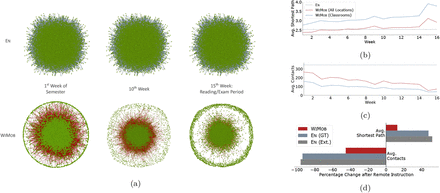
Variation in contact over the semester would naturally impact the severity of disease spread. However, En describes a static network that does not capture such dynamics (Figure 2a). Instead, we find that WiMob shows contacts get sparser as the semester progresses. Figure 2c presents a notable decline in contacts after the first two weeks, which coincides with multiple orientation seminars and the so-called “course shopping” period of Fall 2019. In fact, contact decreases considerably in classrooms, with a steeper slope possibly because of reduction in attendance. WiMob is able to reveal other observable changes, such as drop in contacts during exam period (week 15) and increase after fall recess (week 10). Since, En renders a highly connected static network, which can miscalculate the speed at which a disease spreads. By contrast, the longitudinal behavior represented by WiMob can help universities anticipate disease spread more accurately.
Results show difference in structural characteristics of contact networks from En and WiMob. (a) En describes contact based on classes that students are expected to attend based on their enrollment. En assumes 90% of students to be connected in a single component, but WiMob reveals that on given week only 69% of the academic population is in the largest component (those that do not visit campus are isolated and shown in the circumference). In the first week of Fall 2019, both En and WiMob show high connectivity. However, En does not change, but WiMob reveals that density of connections changes over the semester. (b, c) The difference in the two disease models is because of the difference in structural characteristics of networks built with WiMob compared to En. (b) En depicts campus contacts to be connected closely into a “small world”. WiMob shows that contacts evolve over time. As mobility captures interactions outside classrooms we observe that for the first 6 weeks the shortest transmission path between people is shorter than what is reported by En. (c) Enrolling into a course does not necessitate physically collocating with the class for extended periods (students can also choose to be entirely absent). WiMob reflects this behavior and highlights a decline in average contacts over time. (d) These structural differences can help policymakers anticipate the effect of closure policies by describing how it fragments the underlying contact network. En shows that remote instruction leads to a 94% reduction in contacts and 50% increase in transmission path length (similar to numbers reported in [59], shown as En (Ext.)). However, the estimate is significantly lower with WiMob. As a result, WiMob emphasizes the limits of remote instruction policies and in turn motivates new policies that can be designed and evaluated with actual on-campus behavior.
En overestimates contact-based risk
Campuses can assess risk of an outbreak by characterizing the number of individuals that would be at risk of infection through contact. In fact, En indicates that 99% of the individuals on campus are clustered in a single component — if any of them would have been infected in Fall 2019, everyone in the component would be at risk. From the lens of En a virus can exhaust an entire population with infection very early. However, WiMob shows that only 69% of the population is connected in a single component (Table S3). This difference is because WiMob can distinguish how many individuals are active on campus. Therefore, WiMob provides a pragmatic estimate of risk by grounding it in local occupancy and helps campuses budget for resources better.
WiMob reveals different paths for disease transmission
Reports suggest that a key contributor to cases in the pandemic is actually clustering of individuals in non-academic spaces [39]. However, En does not depict a holistic view of campus contact. It is limited to classrooms and, therefore, fixates on contacts in lectures, while ignoring other spaces. In fact, WiMob shows that in the first 6 weeks of Fall 2019, the shortest path among individuals is smaller than that approximated by En (Figure 2b). With WiMob, we observe new paths in the contact network from situations outside classes. On a given week, WiMob shows the average shortest path with contact is 3.26(± 0.5) when only considering lectures, whereas capturing all contexts reduces the average shortest path to 2.67(± 0.28). Characterizing shorter pathways is crucial for policymakers as closure policies by design aim to disconnect these pathways.
En overemphasizes the impact of remote instruction
Prior work uses En to posit that RI reduces contact and in turn significantly fragments the network for disease spread in universities [59, 7]. To compare policy effectiveness with WiMob, we operationalize RI in our study:
Remote Instruction (RI)
The status quo for data-driven policies offers strictly online instruction for large class enrollment, while continuing the other classes in person. For En we implement this by removing connections between students who are only in contact through courses where size ≥30. For WiMob we remove connections between students if they are only connected because of collocations during scheduled lectures of such courses.
We evaluate the effectiveness of such a policy if it were applied in Fall 2019, with both WiMob and En. Figure 2d shows that RI with En reduces contact by 94% and increases shortest path by 50%. However, the same intervention with WiMob shows a relatively milder impact (contact reduction 45%; shortest path increase 11%). This reinforces that contact outside courses are significant and remain unaffected by enrollment-oriented policies like RI. WiMob provides a more encompassing view of the structural effects to a network and motivates design of more impactful closure policies.
LC yields better infection reduction outcomes with lower burden
As outlined above, En does not capture comprehensively the contact on campus. A campus is composed of many different spaces and En does not have the flexibility to design closure of such spaces or assess its impact. These drawbacks naturally motivate a new approach to design interventions. Since WiMob mitigates the limitations of En, we leverage it to demonstrate the effectiveness of localized closure or LC.
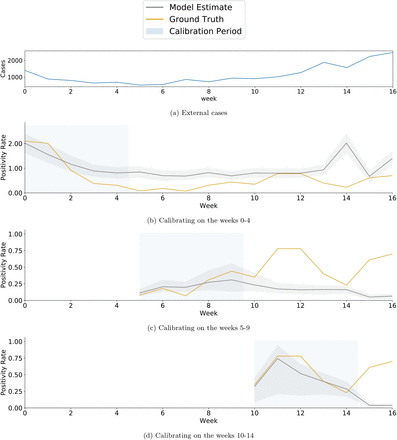
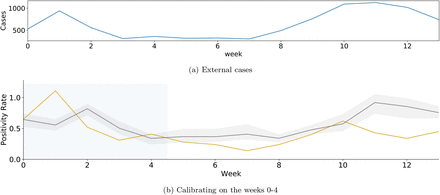
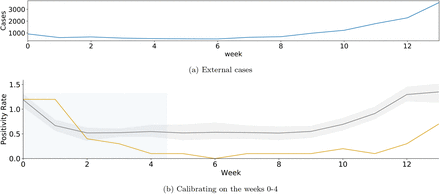
We evaluate the community health outcomes and burdens to campus of closure inter-ventions by simulating COVID-19 with our ABM that uses WiMob to define the contact structure for each day. This is overlayed by a modified SEIR compartmental model for COVID-19. GT also had implemented a robust surveillance program on campus. Hence we calibrate the ABM on the positivity rate for COVID-19 for GT [25] in the first 5 weeks of Fall 2020 also incorporating external seeding from the surrounding Fulton County, GA [40]. We validate our model by predicting future trends for the rest of Fall 2020. For robustness, we perform additional calibrations by varying time windows and university context (details in SI Sensitivity Analyses). We study interventions by applying the ABM over the contact networks produced by WiMob with data from Fall 2019 — a counterfactual to Fall 2020 if no closure had occurred (see SI Simulation Model for further details).
WiMob can model RI and LC interventions with various configurations
In addition to RI, we model LC, which we formalize
Localized Closure (LC)
Prior works show a few locations are responsible for majority spread [10] and restricting movement between regions leads to greater control [33]. We intuitively identify rooms–level spaces that are highly central location nodes in the network. We remove contacts between people who are only connected because of collocating at these locations. While, we employ various centrality algorithms to identify such locations, but for the results discussed in this section we use PageRank [42]). Details in SI Identifying Locations for Closure.
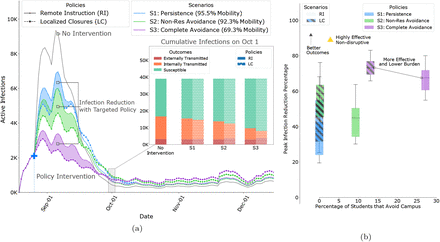
We find that, if COVID-19 spread through Fall 2019 (a regular semester), the cases rise after 7 days (Figure 3a). Therefore, we apply both RI and LC interventions after the first week.
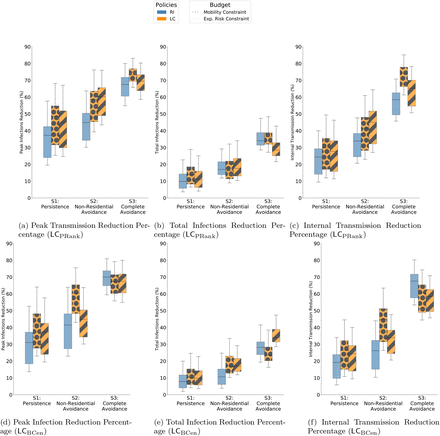
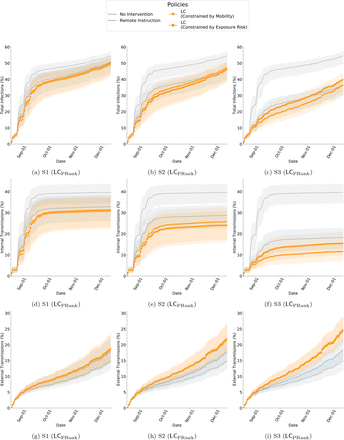
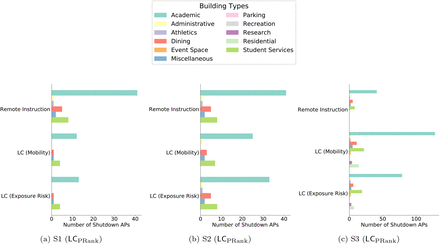
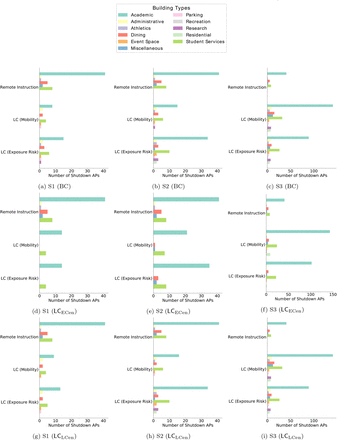
Results of policy interventions with our calibrated ABM on contact networks from Fall 2019, derived from WiMob (a) LC shows improved outcomes (shaded regions) even when constrained to the same restrictions of broader shutdown policies. This holds true especially during the first month after the policy is implemented and is consistent regardless of the behavior scenarios. After the first month, the active infections decline for non-intervention and broader shutdowns appear to be lower, but the cumulative infection count is still higher (inset). The overall decline in infections could be a function of reduced contact (Figure 2b) as well as fewer external infections from the county. It is important to note that new infections are a proportion of susceptible individuals in the system. Since LC restrict spread early, it leaves more people susceptible (to both internal and external infections) later in the semester. (b) LC not only provided better outcomes (for peak and internal infection reduction) they also tend to be less burdening in terms of certain cost dimensions. For instance, in certain scenarios LC forces fewer students into fully online schedules and therefore keep more students on campus.
To make the comparisons between the closure policies, we establish fixed budgets to design LC based on the resource utilization on RI We consider 2 kinds of budgets, (i) mobility reduction — to depict space use on campus, and (ii) risk of exposure — to reflect testing capacity. Also note, response to closure policies can lead to unpredictable side-effects in campus behavior, particularly when a student’s schedule is entirely online. Therefore, we design policies within three behavioral scenarios (each with a varying budget):
S1: Persistence: Irrespective of the locations closed or classes restricted, individuals continue their other visiting behaviors.
S2: Non-Residential Avoidance: Non-residential students stop all visits to campus if they enrolled in at least 3 courses and the policy forces their entire academic schedule online.
S3: Complete Avoidance: Both residential and non-residential students avoid campus if they have at least 3 courses and all move online.
WiMob facilitates the conception of expressive closure interventions. To devise interventions,WiMob estimates how RI uses the budget and then designs LC to match this budget under every scenario. Table 1 describes how the budget for each policy varies. Additional details are present in SI Modeling Policy and Scenarios.
Comparison of different policies in terms of controlling the disease and impacts on campus in Fall 2019.
We present differences between LC and RI based on three infection reduction outcomes; peak infections (maximum active cases on a given day), internal transmission (exposure from infected individuals on campus), and total infections (cumulative cases at the end of the semester). Additionally, we measure the burden of policy interventions with the number of locations closed — requires resources to monitor and maintain super-spreader locations, the percentage of students that avoid campus — disruption to learning outcomes [16, 11], and the percentage of individuals completely isolated — worsens mental wellbeing [48].
LC cause greater reduction in peak infections, while affecting fewer locations
Controlling peak infections relaxes the burden on a university to support positive cases for any given day, and allows resources to be distributed over time. In all scenarios, of our simulation of Fall 2019, we observe that the peak reduction is significantly better in LC (Figure 3) than RI. While RI impacts 58 different locations (classrooms and lecture halls), in S1 and S2, LC achieves better outcomes by closing fewer locations. For example, in S2, RI achieves a 28.9% peak reduction, but LC shows a reductions of 49.3% (mobility budget) and 48.1% (exposure risk budget). This is attained by closing 38 or 50 locations respectively. Therefore, with such policies, policymakers need to restrict fewer locations to remarkably minimize the pressure of active infections on campus (e.g., diagnoses, treatment, quarantining).
LC lead to comparable reduction in total infections, while keeping more students on campus
Universities want to minimize the number of infected cases while ensuring majority of the population remains active on campus to continue successful operation. The total number of infections reduced by both LC and RI are similar. While the differences between policies are statistically significant (Table S3) in some scenarios, the magnitude of these differences might not be practically as important. In contrast, the impact the policies have on the student schedules is remarkably different. RI forces multiple students to adapt to fully online schedules. In the Scenario S2, 9% of students do not visit campus and in S3, 27% of students do not visit campus. On the other hand in LC the number of students expected to avoid campus can be as low as 0 and never exceeds more than 12%. Besides sustaining economic loss to the campus, remote instruction can increase anxiety among students and hinder learning outcomes [11, 61]. Compared to RI, LC offers policymakers a way to defend against turnover in the student population, without compromising overall control of disease spread (Table 1). Limiting the number of students that avoid campus helps preserve on-campus businesses [28, 58] and minimally disrupts the student wellbeing.
LC cause greater reduction in internal transmission without causing further isolation on campus
Universities are responsible for limiting spread on campus, but they must also ensure that aggressive policies do not worsen mental wellbeing of the community. In terms of internal transmission the reduction is significantly larger with LC (Table 1). However, when LC restricts the infections early in Fall 2019, it leaves more individuals susceptible to external transmission. College student behavior outside campus on weekends and breaks is known to impact local transmission [14]. When policymakers consider LC they should also consider policies on re-entry or required testing based on off-campus activities. In terms of isolating individuals on campus, it’s notable that LC and RI are similar in S2. Interestingly, in S3, where LC closes more than 100 locations, the percentage of isolated individuals per week is less than that of RI. This finding implies that LC can keep individuals on campus without forcing them into complete isolation. Here “isolation” refers to no form of proximate con-tact with any individual on campus — extreme social distancing where individuals are not even collocated in the same suite or hall. While social distancing is a recommended coun-termeasure for COVID-19 [1], complete isolation can have adverse effects on psychological wellbeing [48, 36, 43]. Staying completely isolated on campus can increase loneliness and limit social connectedness [36], which are both related to depression [48]. Although the pro-portions are similar (Table 1), LC does not necessarily isolate the same sets of individuals. This qualitative difference could also explain the difference in internal transmissions — LC could be isolating individuals who are less likely to spread the virus.
LC identifies a wider variety of auxiliary spaces
By using WiMob to design LC we are able to identify locations for closure at the granularity level of rooms, including unbound spaces such as lobbies and work areas. First, in S1, we find that most locations that LC targets are a subset of the auditoriums–like rooms where large classes would take place in Fall 2019. Note, LC needs to restrict only a few such spaces to be under the same budget as RI. This is because, under S1, RI policies only alter visits to lectures, while these spaces are used for other purposes during other times (e.g., club activities and seminars). We also note that LC targets ‘high traffic’ locations like conference center lobbies which are typically used as waiting areas or for networking events. Next, in Scenario S2, we see that in addition to spaces mentioned earlier, interestingly LC further restricts the use of smaller rooms (occupancy 13 - 35) which would not be affected by RI (as only classes of size ≥ 30 are offered online). LC also targets areas in the recreation center (which includes locker rooms and indoor courts for 4 - 20 people). This insight indicates that our methodology WiMob is sensitive to other student activities. Moreover, we also find a selection of spaces that would not be frequented by the undergraduate population, such as lab areas and facility buildings like the police station. Lastly, in Scenario S3, LC targets closure of activity in far more spaces than RI. However, the better outcomes can be attributed to the fact that LC diversifies the potential restriction areas. LC now restricts heavily used small study rooms or breakout rooms (for 1 - 6 people). Furthermore, it restricts use of spaces where multiple small groups of people can organically assemble, such as cafes, dining halls, and reading areas. We also observe that LC restricts activity in about 10 Greek Houses but does not target other housing areas — demonstrating its ability to restrict social behavior that could amplify disease spread. Figure S22 shows the diversity in locations for various LC policies.
Sensitivity and robustness analyses
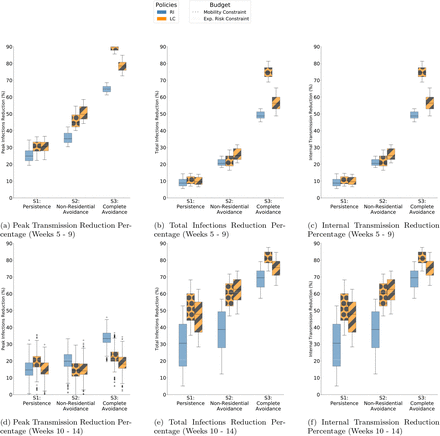
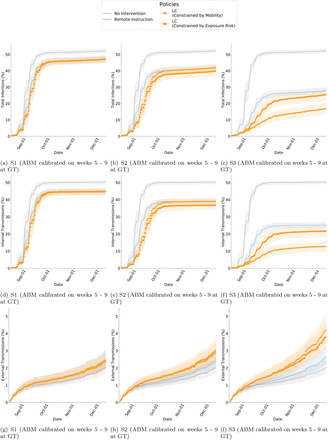
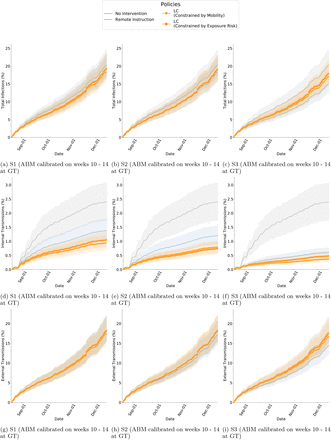
The results above use an ABM calibrated on the positivity rate of the first 5 weeks of Fall 2020. At a university, this rate can be influenced by many latent factors (e.g., mask-wearing, hand washing, distancing, and compliance). To study any effect of these variations on our results, we also calibrated on different time windows throughout the semester. We calibrate on weeks 5 - 9 and 10 - 14 in Fall 2020, and validate on the remaining semester. In both cases, compared to RI, we find that LC still exhibits better reduction in peak infections (up to 90%) and internal transmission (up to 77%). In the original calibration, LC also significantly reduces total infections and maintains the same level as RI, but with the new periods we find total infections are substantially less than RI (Table S9 and Table S10).
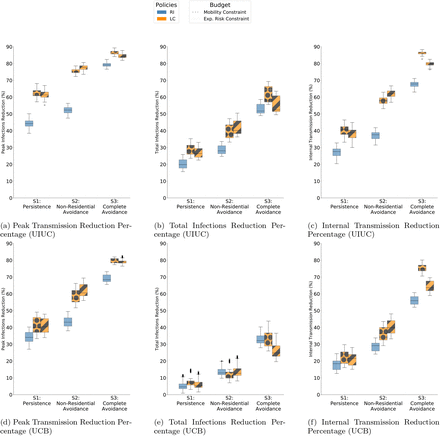
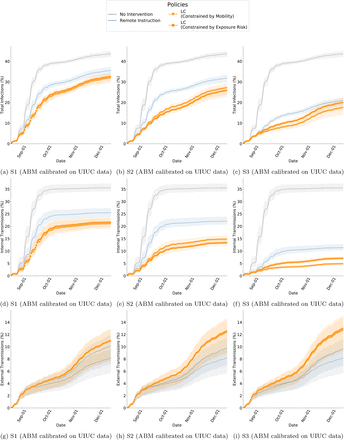
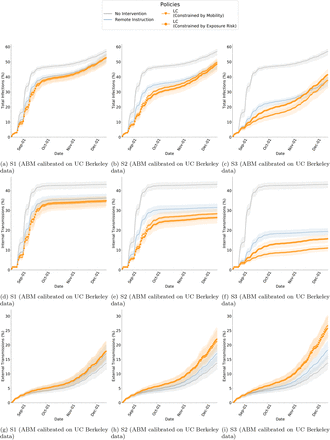
Another important variable for positivity is the wider context of the campus e.g. ur-ban/rural, the surrounding county, city, etc. To investigate this, we also calibrated our ABM on the positivity rate of different universities in the US in Fall 2020 (along with information from their county to seed external cases). Consider this as a hypothetical where the mobility of the GT community remains the same but disease outcomes resemble a different campus. We calibrate on data from University of Illinois at Urbana-Champaign and University of California, Berkeley. We find no remarkable differences from our findings with GT (Table S11 and Table S12).
Discussion
When facing a pandemic, non-pharmaceutical interventions (NPI) are the first line of defense for universities to respond to contagious diseases like COVID-19 [19, 38]. On a campus, a common form of NPI is closure [29]. Universities consider enrollment data (En) to design remote instruction (RI) for closure to support continued operations safely [59]. However, En can misconstrue contact on campus and RI policies can have broad impacts despite their effects on curbing the disease spread. This paper demonstrates that repurposing logs from a managed WiFi network (WiMob) can help design effective localized closure policies (LC). We show that WiMob uncovers rich contact dynamics and provides policymakers multiple dimensions to design policies like LC. We simulate COVID-19 with an ABM that harnesses WiMob to compare RI and LC. Our results present evidence that LC can lead to improved infection reduction outcomes, while simultaneously relaxing burdens on the campus community caused by coarse-grained broad RI policies.
Generalizability for Other Contexts
In practice LC policies should be deployed on campus in conjunction with the other tools as well like testing, tracing, and quarantining. WiMob can complement disease-specific knowledge to identify closure spaces. For example, small indoor spaces with poor ventilation increase the risk of infection for COVID-19 [51], while other algorithm-identified locations for closure might not require closure because mask-wearing and testing have high compliance among users of that space. Further, as a pandemic progresses and public health guidance develops [50], with WiMob, campuses can regulate the restriction of LC policies and anticipate the path to ‘normal’ operations [34, 44] Moreover, WiMob captures various spillover effects that cannot be captured in methods like En. For instance, with WiMob we observe that the mobility in Fall 2020 was 39% of that in Fall 2019 because the on-ground policies lead to certain staff working remotely as well. With additional information, WiMob enables policymakers to model such scenarios and design alternatives like LC with new budgets. Policymakers in universities can use WiMob as a versatile tool to explore dynamic intervention strategies as well. In this paper, LC interventions are non-adaptive fixed policies throughout the semester. Since staggering policy restrictions could have variable impact on campus [65].
However, WiMob could help identify locations from different mobility phases (e.g., the same week from a prior semester) and assess the effects of closure policies. Additionally, depending on campus priorities and resource limitations, different campuses can use this same data to model policies differently. The effectiveness of reopening policies is expected to be sensitive to a campus’ specific context that includes physical infrastructure, overarching guidelines, and human compliance [5]. For certain campuses policies might not need to be constrained by exposure risk as testing might be frequent, ubiquitous, and voluminous. Other campuses could have limits on quarantining capacity. Policymakers might even consider the cost tradeoffs by actually forecasting actual financial losses incurred by reduction in mobility [6], or valuate loss of services based on community needs [53]. We elaborate on these considerations in the SI Implications for Policy Design.
Operational Considerations
Beyond assessing cost-benefits, universities also need to consider practical methods of obtaining, storing, and processing mobility of the community as WiMob. University can access logs from the managed network internally as it is passively collected. Moreover, it does not require any new form of surveillance sensing but universities must revise terms of use and stay sensitive to community perspectives. While aggregate data on population mobility is valuable for many applications [64], which includes informing pandemic response [8], the major privacy challenge with localization data is to avoid accumulation [56]. Instead, operational applications need to conceive approaches that only retain processed insights on locations to shutdown but not individual data. Similarly, any operational use needs to have pre-established access limitations on what stakeholders can learn from the data [4] (e.g., decision-makers can only get a list of candidate locations to close). In the SI Discussion, we further detail approaches to reconcile privacy, ethics and legal considerations.
Limitations and Future Work
Lastly, for future investigations of better closure policies, researchers and policymakers need to be cognizant of the limitations of our work. Our analyses do not represent heterogeneity among individuals and therefore our simulation does not account for intrinsic vulnerabilities [31, 43, 22] and difference in mobility behaviors of demographic groups [10]. WiMob can be extended with other streams of data to introduce variability in the population and devise new forms of LC to protect the most vulnerable community members. Additionally, our work explores the extremes of the range of behavioral responses to closure interventions. Henceforth, researchers and policymakers can model more nuanced spillover effects that interpolate between the scenarios we describe, as well as extend them. Further discussion in SI Limitations and Future Work.
Methods
This section summarizes (i) the data used to derive contact networks and policies, and (ii) the dynamics of our simulation model and calibration approach. Additional information for every subsection is present in SI Methods.
WiFi Mobility
Data Use and Access
The IT management facility at GT accumulates WiFi access point logs over time. This is common in most universities with managed WiFi infrastructure. We actively collaborated with IT management to define safety and security safeguards that allow us to obtain a deidentified version of these raw logs. Before accessing the data we established a data-use agreement and an ethics protocol that was approved by the Institutional Review Board (IRB). For the WiFi data, we were provided access to logs from Fall 2019 and Fall 2020. We process these logs to characterize mobility (WiMob) and it encompasses all 40, 000 unique individuals that connected to the network via 6, 959 different access points [13]. The logs do not contain any personally identifiable information and locations are also coded. For En we only use aggregate insights for enrollment, which are derived from course registration transcripts. Note, we do not cross-identify any students. We use publicly accessible course schedules to approximate schedules of de-identified nodes and infer if they are students or staff, and non-residential or residential. We elaborate on our data in SI Data.
Contact and Movement Networks
WiMob leverages the logs to create bipartite graphs Kt, for each day t, which connect P users to L access point locations (Figure 1a). Any edge, {p, l} i indicates the ith instance when a p was dwelling at l. These edges describe the time period of dwelling. Subsequently, by comparing all edges in Kt we can infer if different individuals are collocated near an AP to create a contact network, Gt, for each day t — between collocated p ∈ P. These networks feed into the ABM at every time-step. Similarly, by inspecting the sequence of dwelling locations for any p in graph K, we compute a mobility network, Ht — between locations l ∈ L. We provide more details of our approach in SI Data Processing and in SI Modeling Collocation and Movement.
Modeling Policies
We compare the disease outcomes and burdens of 2 policies, Remote Instruction (RI) and Localized Closure (LC), both of which are modeled with WiMob. For RI we infer enrollment size of each course in Fall 2019 by determining the number of unique individuals that visit lecture locations during scheduled times. After the first week, we apply the RI by removing all visiting edges in Kt for any lc ∈ LRI if visits were during lecture times of course c with an enrollment ≥ 30. This helps create counterfactual contact networks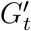 
. The removal of edges from K describes the mobility budget of RI and the structure of 
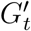indicates the risk of exposure budget. We design LC with these budgets by identifying locations for closure (LLC) with different algorithms, such as PageRank, Eigenvector Centrality, Load Centrality, and Betweenness Centrality. When a location is closed, we remove all edges in Kt connected to any lx ∈ LLC. We aggregate the movement graph Ht over a week and apply the algorithms to identify locations. Subsequently, we identify the number of top-ranked locations to remove such that the resultant counterfactual contact network G”t has is within 1% of the budget. The budgets vary for different behavioral scenarios and we only compare policies within the same scenario. This is further elaborated in SI Modeling Policies and Scenarios.
Disease Simulation
Agent-Based Model
We construct an agent-based model (ABM) that captures the spread of COVID-19 between individuals active on campus. This ABM leverages the contact networks produced by WiMob. The simulation iterates a time-step each day and the underlying contact networks i.e., Gt for no interventions,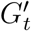 
for RI, and 
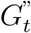for LC. Our ABM follows a modified version of susceptible–exposed–infectious–removed (SEIR) template that disambiguates the infectious compartment into asymptomatic and symptomatic. New infections are introduced to the model either externally or internally. External transmission arises because individuals can contract the virus outside campus and bring the infection back for local spread [24, 39]. We adopt data of positive cases from Fulton county [40] with a scaling factor α to estimate the probability that a susceptible individual, who is active on campus, was infected from interactions outside campus. This is to account for any commute outside campus during the pandemic. Internal transmissions are determined by p, as the probability of susceptible individuals in contact with an infectious one. We calibrate the parameters related to disease transmission by training and validating our models on the positivity rate reported by GT surveillance testing [25]. SI Agent-Based Model details the disease progression and describes the various parameters.
Calibration
We estimate the ranges of optimal parameters for disease transmission by minimizing the root means square error (r.m.s.e) between the Georgia Tech surveillance testing positive rates [33, 25] and the observed positivity rate of the model every week— percentage of new asymptomatic out of the total testable population. The surveillance testing conducted by Georgia Tech is designed for detecting individuals who contracted Covid-19 without showing Flu-like symptoms within the community [33]. We calibrate the model on the positivity rates on the first 5 weeks of Fall 2020. To attain a point estimation of the optimal parameters, we fit the model to predict trends in the remaining weeks by running a numerical optimization algorithm, Nelder-Mead [25]. To account for quantitative uncertainty, we estimate a range of parameters, within 40% of optimum r.m.s.e. Note, this calibration characterizes latent factors associated with pandemic-related cautious behaviors, including the relationship with external transmission. And these factors could be related to “county characteristics, partisanship, media consumption, and racial and ethnic composition” [1]. Since the effectiveness of shutdown policies can vary by time period and county. In SI Sensitivity we discuss hypothetical variations where the mobility behavior of GT remains constant but disease outcomes change based on time period of calibration and positivity rates from universities at different counties in the U.S. See SI Calibration for details on the calibration process and results are in Table S4.
Data Availability
Deidentified version of this data can be requested by interested parties through appropriate data use agreements
Supplementary Information
Supplementary Methods
In this section, first, we describe the primary data source for mobility models (WiMob), the data used for calibrating our simulations, and for comparison of contact networks with methods using enrollment data (En). Next, we describe how we construct counterfactual mobility networks under the two main policies of interest in our study: remote instruction (RI) and localized closures (LC). Finally, we describe an agent-based-model (ABM) of disease transmission, which has a contact structure based on WiMob, and how this model was calibrated.
Data
WiFi Mobility
We use data provided by the IT management facility at Georgia Institute of Technology (GT) which accumulates WiFi access point (AP) logs over time. The primary use of WiFi network logs is for maintenance and security purposes. We mine these logs post-hoc to describe the mobility of individuals on campus, which we refer to as WiMob. Here mobility is expressed by visits to certain locations that are demarcated by a corresponding AP. WiMob can also describe dwelling (duration of visits) and collocation (dwelling in the presence of others around the same AP).
The campus WiFi network spans 6959 APs distributed between 240 buildings (and some outdoor locations). We label APs according to which building they are inside, along with the closest room or space (e.g, hallway, lobby, suite, cafe, etc.). The AP may or may not reside inside the room, however, in most cases, only a single AP is associated with space. For less than 5% of the APs, the AP shared association to space with another AP. This manyto-one mapping is typically in the case of large halls and auditoriums. We resolve such many-to-one associations by using APs as a proxy of the space they are associated with. Therefore, individuals connected to different APs in the same space will still be identified as collocated. Similarly, an individual could connect to the network with multiple devices. However, less than 1% logs show that a user is connected to multiple APs around the same time. Therefore, WiMob is agnostic to which device connects to the APs to proxy the presence of the individual. For this study, we obtain the WiFi network logs retrospectively for all of Fall 2019, and the data for Fall 2020 was provided on a per-day basis. Each day, approximately 33, 000 different people connect their devices to the WiFi network on campus. Overall in Fall 2019, approximately 40, 000 different people connected to the campus network.
Note, that GT’s managed WiFi network is not equipped with any Real-Time Location System (RTLS) [9, 27]. RTLS systems use Received Signal Strength Indicator (RSSI) values from multiple neighboring APs to provide high precise localization of individuals in terms of time and space. However, deploying such systems requires surveying the entire network. Additionally, precision localization raises more privacy concerns. These factors together make it challenging for universities to justify the deployment of RTLS, unlike small retail settings that can monetize RTLS insights directly (e.g., insights on footfall can be tied to improving revenue).
Asymptomatic surveillance testing data
We calibrated the ABM using the publicly reported positivity rate on the GT campus as reported through the asymptomatic surveillance and diagnostic testing program [33]. The testing program used pooled saliva sample surveillance with follow-up diagnostic testing. The positivity rate was reported each day, but individuals must wait at least 1 week between tests. We aggregated the positivity rate by week during the Fall 2020 semester.
Confirmed case data
When calibrating our ABM, we considered the reported confirmed cases in Fulton County [40], the county in which GT is located. The ‘Confirmed COVID-19 Cases’ reported in this dataset are cases that have been confirmed with a positive molecular (PCR) test. We considered cases during the Fall 2020 semester to inform external transmissions in the ABM.
Enrollment network summary statistics
We compare structural properties of contact networks constructed with WiMob to contact networks constructed from GT’s course enrollment transcripts (En) — the aggregate statistics as reported in [45]. The En network was based on Fall 2019 transcripts for GT’s Atlanta campus. These were cleaned to account for cross-listed courses and was used to determine which students were classmates with each other to form a contact network.
WiFi Mobility Models
Inferring location from Logs
WiMob is our approach to describe contact between people and movement of people between locations. The first step requires using WiFi network logs to infer when individuals were at specific locations on campus by determining when devices were connected to the corresponding APs. Our system mines the WiFi network logs that are populated via the Simple Network Management Protocol (SNMP) — a standard and widely used monitoring protocol to organize device association behavior to a WiFi network. Periodic SNMP updates can be caused either by poll requests to the APs that log which devices are associated with it at that time. However, devices can appear invisible to detached from an AP for multiple reasons, for example, when devices are idle. Otherwise, SNMP updates can occur whenever a new device connects, which is typical when individuals move between APs. Our approach exploits this factor to first mine periods when individuals are moving, then identify periods of dwelling between movements, and finally determine collocation when two or more individuals are dwelling near the same AP. This system follows from other studies that mine WiFi logs [18, 57] and the detailed processing pipeline and evaluation is presented in [13]. This system to infer collocations has been tested against lecture attendance and reports a high precision of 0.89, but a relatively lower specificity of 0.79 [13]. While it is not likely to show false-positives, it has a possibility to erroneously mark people absent from a location even though they were there. However, for the purposes of our study, a contact network is made over an entire day and it only needs a single collocation instance for us to consider contact. And therefore we believe this limitation would not significantly affect our models.
In a managed network, SNMP updates the logs by describing device association to an AP at a certain timestamp. WiMob mines these logs to characterize mobility as a bipartite graph. The nodes are partitioned to describe people nodes (e.g., P1, P2) connected to locations nodes (e.g., L1, L2). Every edge across the partition describes people visiting locations on campus during different times (e.g., t1, t2). Projecting the bipartite on people nodes helps construct a contact network (e.g., P1 and P2 were collocated at L1 at t1), while projecting it on locations helps construct a directed movement graph (P2 dwelled at L1 and then at L2).
Characterizing Logs as Contact and Movement Networks
After inferring where an individual is located on campus, we represent the entire community behavior as graphs. We describe a bipartite graph, K, that shows when a user is at a given location on campus (Figure S4). This bipartite graph has edges connecting a set of m people, P, to a set of n locations, L. An individual can have multiple edges connecting to the location if they visited that location multiple times (e.g., t1, t2). The edge data contains the start and end times of these dwelling periods. For these bipartite graphs, we make a projection on set P to describe collocation. This projection graph, G, contains an edge between users if they were visiting the same location during overlapping times. Since we do not use RTLS, our approach can only identify if people were in the vicinity of the same AP, but does not describe the distance between them. However, it can reasonably determine collocation in the same room [13]. Since our study is limited to localizing people indoors, we adapt the definition of proximate contact [27] where people might be “more than 6 feet but in the same room for an extended period”. In our work, we use a lower bound threshold of 40 minutes to determine proximate contact. Therefore, individuals are only considered in contact when they are collocated in a room for 40 minutes or more. This threshold was set up to account for typical lecture duration on campus (for standard 3-credit hour courses taught 3 times a week). Every edge between two individuals contains a list of locations where they were possibly in contact. G forms the basis of the contact-network that we use an agent-based model to simulate. Alternatively, we also make a projection on the set L. This projection is a directed graph, H, where an edge from Li to Lj represents movement from the first location to the next within a span of 60 minutes. GT’s large urban campus with pedestrian pathways and motorized transit services enables direct movement between any two places on campus within the threshold. The 60 minutes threshold helps discount erroneously labeling returning from outside campus (e.g., non-residential students visiting two different locations between 2 days). H effectively describes how locations are connected and which locations could be more conducive to attracting and disseminating the virus. As a consequence, the H helps inform policy design. We compute the bipartite graph and its projections for each day of the semester.
Modeling Policies and Scenarios
RI: Offering Large Classes Online
As a response to COVID-19, prior work has recommended using En to enforce a form of RI— moving classes large to an online remote instruction setup while other classes are offered in–person [26, 7, 59]. While we have access to aggregate insights on En contact networks, our study protocol prohibits us from accessing course-specific information at an individual level. Therefore to infer individual enrollment, we analyze the edges of the bipartite graph K. For this, we first scrape the GT’s course roster for Fall 2019 (filtered to only represent the Atlanta campus). This process provides us with a location and weekly schedule for every lecture conducted on campus, including its various sections. With this information, we are able to identify which edges represent visits to lectures, and subsequently, we can account for unique visitors to a lecture. Thus, we can first identify the number of unique individuals on campus who are enrolled in classes. The aggregate data from course enrollment reports that 21, 299 students were enrolled in Fall 2019. In comparison, our inference identifies 22, 248 students. The excess number can be explained by the fact that our method does not distinguish between instructors, TAs, and students. Next, we study the unique visitors to every lecture in the scraped course schedule which gives us an estimate for the size of every class. Given the limitations of our data processing, actual enrollment sizes could be larger, but our process is less likely to count false positives [13]. Finally, to model RI, for the contact network Gt, we create a counterfactual network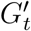 
for each day t. These exclude collocations that took place at lecture locations during lecture times. If two people were connected solely by proximity during lectures — in a class with large enrollment — they will appear disconnected in the counterfactual network.
LC: Closing Important Locations
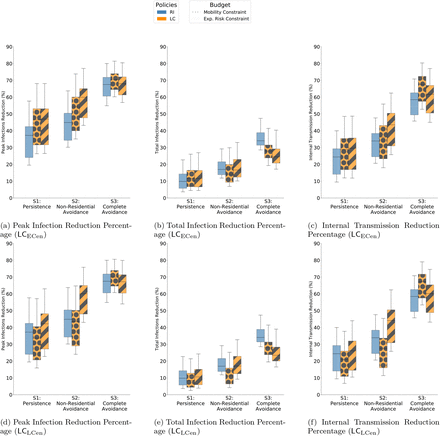
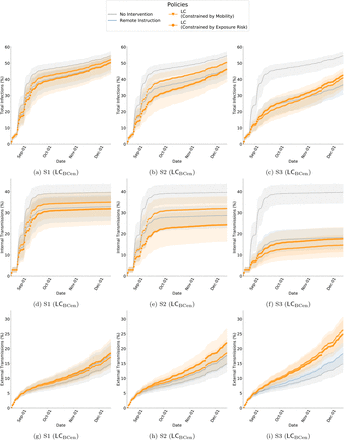
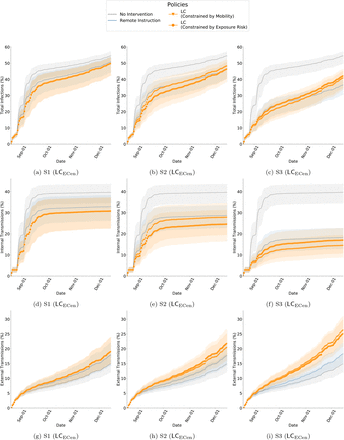
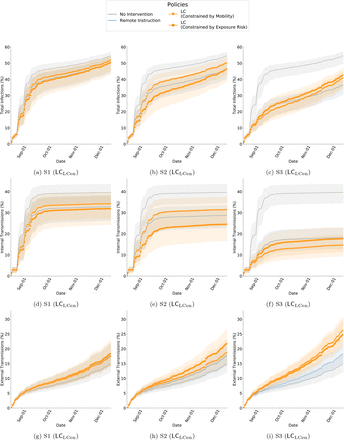
This article demonstrates the effectiveness of localized closures,LC, which are targeted interventions to seize mobility at different spaces on campus. For this, we identify important locations on campus by analyzing H. In the main paper, LC uses PageRank [42] as an illustrative algorithm to identify important location nodes. For robustness, we apply various additional algorithms to identify highly authoritative nodes in H — betweenness centrality [15], eigenvector centrality [5], and load centrality [29]. In the SI Appendix, we distinguish these different policies as LCPRank, LCBCen, LCECen, LCLCen. Since RI captures a weekly schedule to determine enrollment, LC is implemented to find locations based on behavior from the past 7 days of mobility. We apply the weighted version of the algorithms mentioned earlier on the directed graph representing movement, H. The edge weight is based on the number of instances of movement between any Li and Lj. After sorting the locations by importance, we determine the number of locations to shut down based on different budgets induced by RI— mobility and risk of exposure. For this purpose, we take the approach of a greedy algorithm which successively removes highly-ranked locations till the constraint is met (within 1% margin of error). Similar to RI, LC also render counterfactual collocation networks, G”t for each day t. In these networks, we remove instances of collocations that occurred at the shutdown locations. Figure S22 and Figure S23 shows the categories of buildings where different spaces are closed by LC policies.
Inducing Budgets and Characterizing Behavioral Scenarios
We now describe how we compare the RI and LC policies. First, we consider the effects of these policies under three behavioral scenarios. These scenarios express the spillover effects of closure that lead to students avoiding campus entirely because their entire schedule is forced online. This analysis assumes that the motivation to be present on campus is determined primarily by enrollment. We consider that, if a student has a full course load (enrolled in a minimum of 3 classes) and all their classes are offered online, that student might have less incentive to visit campus at all (for any engagement) and thus practice Avoidance. Since LC could end up closing classrooms, it can also lead to academic schedules being affected and elicit Avoidance behavior. As a result, we describe three scenarios. Persistence, is the preliminary, or null scenario, which represents no Avoidance. This counterfactual collocation graph only removes edges directly affected by RI or LC. The second scenario we model is Non-Residential Avoidance where only non-residential students with full online schedules stop visiting campus entirely. Here the counterfactual graph will remove all edges of non-residential students with fully online schedules. Lastly, the third scenario we model is Complete Avoidance where any student with fully online schedules stops activity on campus entirely (including residential students). Here the counterfactual graph will remove all edges from any student with fully online schedules. Since our study protocol prohibits us from mapping our data to other sources, we heuristically infer which individuals are likely to be residential and which are not. We label individuals as residential when they dwell an average of at least 15 minutes at residential locations between 6pm and 10am, on workdays (Monday–Thursday).
Under each scenario, we limit the number of locations that can be closed under the LC policy to ensure the level of restriction is constrained to be similar to the RI policy. We limit the number of locations under two types of restrictive budgets. The first budget is based on mobility, which is the percentage of edges remaining in the bipartite graph if a policy were to be implemented. The second budget is based on exposure risk, which is the number of unique individuals who would be in the 1-hop collocation neighborhood of positive individuals. We compute this budget by randomly sampling 2.5% of the population as positive, based on the highest 7-day average positivity rate reported by GT [25] in Fall 2019. Note, however, the effect of RI on campus can vary in different behavioral scenarios, thereby changing the budget available to design a comparable LC policy. For instance, the number of people at exposure risk is much lower in Complete Avoidance. As a result, we build multiple alternate networks representing the effect of policies under counterfactual behavioral scenarios.
The infection reduction outcomes and burdens of different policy interventions (under various scenarios and budgets) is described in Table S5 — Table S8 presents boxplots that compares the distribution of disease control outcomes. Figure S14 — Figure S17 show cumu-lative plots of disease control outcomes.
Agent-Based Model & Simulation
Agent-Based Model
We constructed an agent-based model (ABM) that captures the spread of COVID-19 between individuals active within the GT community. The model is used to evaluate the effectiveness of different policy interventions. We consider a modified version of the SEIR framework for simulating the spread of COVID-19 [39, 10] by using an underlying contact network given by WiMob. Figure S5 shows the compartments of the framework. The susceptible state (S) represents individuals who have not been infected and can contract the disease by having contact with an infectious individual. The exposed state (E) is canonically equivalent to the “incubation period” and is similar to the pre-symptomatic state found in related work [44, 20]. Individuals are considered infectious when they are in either the asymptomatic state (Asym) or symptomatic state (Sym). Individuals in the asymptomatic state are assumed to be the major “spreaders” [20] and transmit the infections to susceptible individuals before they are recovered (R) [26] — after 7 days [20]. Since asymptomatic is considered a state of mild severity [37], individuals in this state do not have a risk of fatality. By contrast, for individuals in the symptomatic state, will be eventually isolated (Iso) (e.g. self-quarantine, or hospitalization on campus). Once in the isolated state, they cannot transmit the disease to individuals in the susceptible state. Unlike the asymptomatic track, the symptomatic state is considered critical severity. Therefore, after moving to the isolated state, individuals have risk of fatality and entering the death state (D). If the isolated individual survives, they enter the recovered state. We assume immunity is preserved and therefore after recovery the individual is no longer susceptible.
(a) The schematic of the compartments in our modified SEIR model. By the design of the GT surveillance testing [33, 25], the total testable population is defined as the summation of susceptible, exposed, and asymptomatic. Infectious persons are in either symptomatic or symptomatic. For every effective edge in the mobility network, a susceptible individual that is exposed to an infectious person becomes infected with probability p. Individuals may also get infected due to an exposure not captured by the WiMob network which occurs with probability Iout(t) on day t. account for new infected cases. (b) The mobility behavior represented by WiMob changes every day of the semester (shown weekly here). The contact network constructed from WiMob forms the underlying contact structure of the ABM.
Definitions
Let t = {0, 1, 2, 3, …, T} be the index of days in simulations. We denote the sequence of dynamic collocation networks indexed by day t, as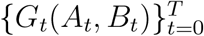 
. At is the set of vertices, i.e. individuals on campus, and Bt is the set of edges. The universe set of the population throughout the simulation time period is given by 
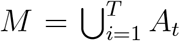. For convenience, we use ai ∈ M to index every person in the universe population set.
The SEIR model consists of seven compartments. Each of these corresponds to a function of population subsets with respect to day t: susceptible S(t), exposed E(t), asymptomatic Asym(t), symptomatic Sym(t), isolation I(t), recovered R(t), and dead D(t). For example, ai ∈ I(t) means ai is in the isolation state at day t. We use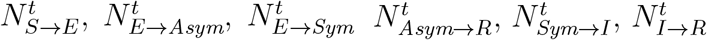 
, and 
to denote the transitions between states between day t and day t + 1.
Model Initialization
The entire population M is fixed where M = S(t)+E(t)+Asym(t)+Sym(t)+I(t)+R(t)+D(t) for all t. To capture the positivity out of the students coming back to campus at the start of the semester, we initialize the system by setting a subset of M into Asym(0) and the reminder into S(0). The initial percentage of asymptomatic is described by:
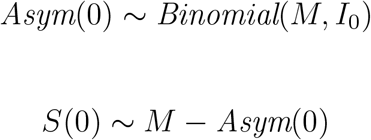where I0 is a parameter defined as the initial percentage of Asymptomatic at day t = 0.
New exposures
We consider two ways that an individual in the ABM could be exposed: (i) exposures that occur due to contacts among individuals captured by the mobility network (internal transmission) and (ii) exposures that occur due to contacts that occur outside of the mobility network (external transmission).
Internal transmissions happen exclusively among individuals in the model. On any given day, an edge becomes effective, when one of the susceptible individual comes in contact with the other which is infectious, i.e. asymptomatic or symptomatic, individual. Therefore, for every effective edge between two such people, the probability of the susceptible individual getting exposed is described by the transmission probability p, which is another model parameter. The probability for an susceptible individual ai entering exposed at the end of day t is given by the following function:
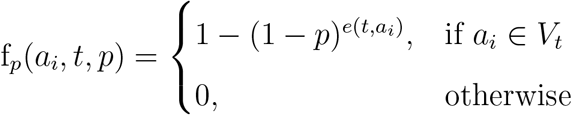
Here, e(t, ai) is the number of effective edges of individual ai at time t. Since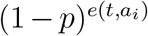 
is the probability that ai does not contracted the disease at time t under e(t, ai) Bernoulli trials, 
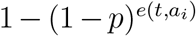is the probability that at least one effective edge leading ai to exposed.
In addition to exposure due to internal transmission, we also consider new exposure due to external transmission. We consider external transmission to be exposure resulting from the physical collocations outside the scope of mobility network. For instance, the WiMob does not capture the connections between individuals without access to the campus WiFi or someone contacting infectious persons outside the campus. To reflect this risk in our model, for any day t, Iout(t) describes the probability of infection on day t from a collocation that is external to the mobility network. We assume that the probability an individual is infected due to an external source is proportional to the number of cases in the broader community. Therefore, we model the probability of external infection as a function of confirmed cases in Fulton county, where GT is located [40]. Ct represents the confirmed cases reported by Fulton County where Cmax is the maximum number of the cases over the whole period, Iout(t) is given by
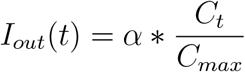where α is a parameter scaling the normalized confirm cases in the surrounding county. The resulting number of external infections on day t is then modeled to be are Binomial with |S(t)| trials with probability of success Iout(t).
In summary, for every day t > 0, the overall number of individuals that become newly exposed is represented as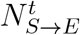 
which is the result of both external and internal transmis-sions.
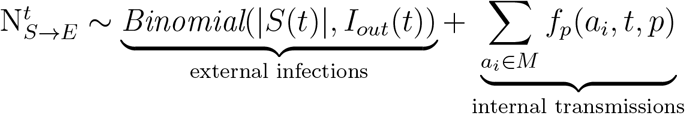
Model dynamics after exposure
After exposure, individuals in the model will progress through other disease states in our model. We update the number of individuals in each state daily to reflect transitions between them. The transitions between the states on day t are summarized according to the following equations:
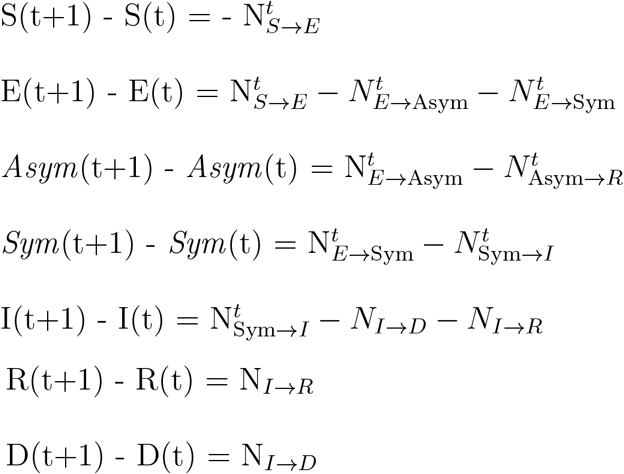
After an individual has been exposed, they will spend ΔS days in an incubation period. At day ΔS after their exposure, individuals will become a symptomatic infection with probability pS. Otherwise the agent will become an asymptomatic infection This process is given by the following two equations:
Individuals who enter the asymptomatic state will recover after ΔAsym→R days since they were first exposed. Thus, we represent the number of transitions from asymptomatic to recovered on day t as:
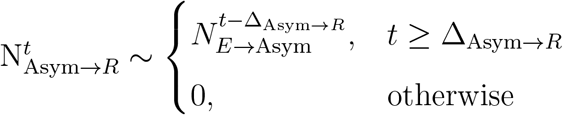
On the other hand, individuals who enter the symptomatic will eventually enter the isolation state [20]. The time that individuals spend in the symptomatic state before entering the isolated state is normally distributed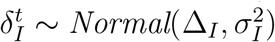 
. We simulate each individual’s transition between symptomatic and isolated by using a sampling function Γ(ai, t, Δt) and a function τ (ai, t) that returns the days since exposed respectively:
Model Parameters of the ABM
The aggregated transitions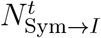 
between symptomatic and isolated is the sum of the distribution above on each day t.
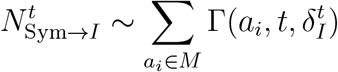
Individuals who enter the isolated state may end up with one of two states: dead or recovered. We defined 
as following another binomial distribution with parameter pD:
The transitions between isolation and recovered is quite similar to the transitions between symptomatic and isolation except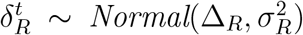 
where ΔR and σR are the two parameters standing for the mean and standard deviation of days for an individual in the isolation state entering recovered since the first day of infection. This leads to:
Model calibration
Most of our model parameters can be estimated from previous studies (see Table S2). However, three parameters in our study are not easily estimated from previous studies: (1) the proportion of the agents that begin the semester asymptotically infected, I0, (2) the probability of transmission between a given infectious individual and susceptible individual given a contact in the mobility network, p, and (3) the scaling factor α used to determine probability of transmission due to contact outside of WiMob network on day t, Iout(t) (see ()). We fit these three parameters to the published weekly positivity rate (percentage of asymptomatic cases) as reported by GT’s asymptomatic surveillance testing program [33]. To fit the parameters, we performed calibration to minimize the root mean square of error(r.m.s.e) between the simulation estimates of the weekly positivity rate and the observed weekly positivity rate on GT’s campus of the Fall 2020 semester as reported by the surveillance testing program.
To perform the calibration, we used two sets of public data pertaining to 2020 Fall semester at GT: (i) the confirmed cases in Fulton County [40], and (ii) the aggregated surveillance test positivity rate for each week [33]. The former helps estimate the daily external infection percentage. The latter is the ground truth trajectory we fit our model on. We consider the data aggregated by week because each individual on campus can only get tested once per week. The positivity rate provided by the surveillance testing data can be interpreted as the estimated percentage of new asymptomatic cases out of the total testable population which includes susceptible, exposed, and asymptomatic — with an assumption that every testable population get tested at the same rate.
To formalize the calibration problem, let Rw be the surveillance-testing aggregated result at week w. Let S(I0, α, p, w) be the function of the simulation model which returns the percentage of new asymptomatic in week w out of the total testable population. For every combination of parameters, the predicted result for each week w is estimated by taking the average of N simulation outputs. The objective function is:
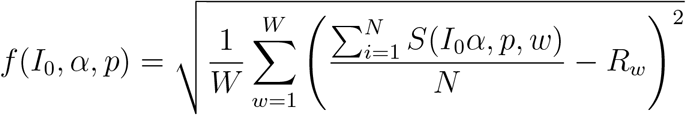
The optimization problem is:
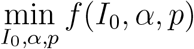
We fit our model to the first 5 weeks of Fall 2020 and validate the results on the remaining weeks. After obtaining the optimal set of parameters, for robust comparison of policies with different viral variants, we generate a range of parameters by compromising the r.m.s.e within 40% of the minima [10]. First, we implement the Nelder Mead method [25] to discover the optimal set of parameters that minimizes the r.m.s.e. Next, we sample 40 different combinations of parameters within 40% of the minimum r.m.s.e to estimate the means and standard deviations of these parameters (Table S2). Throughout this paper, we pool together all simulation results across those parameters over multiple runs (N = 15) and report the 2.5th and 97.5th percentiles of the simulation outputs for every policy experiment.
Sensitivity Analyses
In this section, we design complementary experiments to inspect the robustness LC policies under different setups and calibration approaches. These variations are defined as follows:
Calibration periods (V1): For the results in the main paper, we discuss results with our ABM calibrated on the first 5 weeks of surveillance testing data. For additional analyses, the model parameters are re-estimated based on the surveillance data from week 5 - 9 and 10 - 14 in Fall 2020 at GT. The calibration is validated on the remaining weeks in the semester. Figure S6 shows the calibration and validation. The results of policy comparison with these variations can be found in Table S9 and Table S10, for weeks 5 - 9 and 10 - 14 respectively. Additionally, Figure S12 shows boxplots to compare the distributions of different policies, while Figure S18 and Figure S19 show cumulative plots of the disease control outcomes, for weeks 5-9 and 10-14 respectively.
Campuses and counties (V2): For the results in the main paper, the calibration of our ABM reflects certain latent factors inherent to GT that could affect both mobility behavior as well as testing results. To complement this we consider calibrating our data under different settings informed by surveillance testing from other similar large universities. This analysis is intended to represent the GT community in a different geographic setting, which is influenced by a different surrounding community, policies and resources. The new parameters are estimated based on the first 5 weeks of surveil-lance testing from the University of Illinois at Urbana-Champaign (UIUC) and the University of California, Berkeley (Berkeley) [31, 38], and the corresponding county data [12, 11] The calibration is validated on the remaining weeks in the semester. Figure S7 and Figure S8 show the calibration and validation for UIUC and Berkeley respectively. The results of policy comparison with these variations can be found in Table S11 and Table S12. Additionally, Figure S13 shows boxplots to compare the distributions of different policies, while Figure S20 and Figure S21 show cumulative plots of the disease control outcomes.
The estimated parameters with these calibration variations are described in Table S4. Both RI and LC are evaluated in the same infection reduction metrics and burden metrics again under scenarios S1, S2, and S3. Since the budgets are structural (mobility, and exposure risk) the LC policies are unchanged among the variants. Moreover, since the burden metrics are structural, those results are invariant.
Supplementary Discussion
Implications for Policy Design
To evaluate the efficacy of policies, we inspect infection reduction by simulating the disease with contact networks from Fall 2019. Since managed WiFi networks accumulate logs for long periods of time, policymakers can use WiMob to model data from previous semesters and experiment with closure policies like LC. We show that WiMob can provide retrospective disease–mitigating insight into multiple counterfactual scenarios. For instance, policymakers can consider studying seasonal behaviors over multiple semesters for more robustness. Since the underlying data is longitudinal, it provides the flexibility to realistically assess policy interventions at different time points and also study updating policies. Restricting movement on campus at different time-points is known to exert varying degrees of control on disease spread [10]. Our data also shows that mobility on campus varies across the semester and therefore, allows policymakers to consider loosening shutdowns depending on the phase of the semester.
Policy design is determined by practical budgets. We model two kinds of budgets, mobility reduction and risk of exposure. The former represents disruptions in space utilization, availing services, and social life. The latter translates to the testing burden on campus. Our analysis determines the budget in different scenarios by observing the changes to the graph when large classes are moved online. This is to ensure an equitable comparison with targeted policies. However, in real situations these budgets can be relaxed or restricted based on that campus’ preparedness to tackle a pandemic. For instance, a hypothetical campus that can test everyone every day might not be constrained by risk of exposure. Alternatively, policymakers can model other tangible budgets such as the capacity in isolation wards or available hospital beds. This can be informed by practical limitations of the campus. Similarly, this paper only assesses limited forms of cost, e.g., students avoiding campus or closing locations. From a financial perspective, university campuses can digitize their core service— education—but still realize losses from other curtailed services [23, 6, 58]. When students avoid campus it can lead to direct losses from meal passes and parking and also quantifiable losses to learning outcomes [2, 16] Policymakers can compute actual costs by complementing this data with information from other sources (e.g., revenue generated by cafes and stores on campus). This can help qualifying WiMob to reflect different costs and in turn help design policies that optimize for financial losses. Different campuses have different priorities and challenges in implementing policies.
Privacy, Ethics and Legal Considerations
We purposefully compare our prototype targeted policies against moving classes online because of practical budgets within the university. Both the WiMob and En based contact networks are derived from archival data accumulated by universities. This does not require instrumenting campus or its community with any new form of surveillance infrastructure. However, its use for a different purpose demands approval by an IRB. Moreover, acquiring these kinds of data would require collaborating with data-stewards (e.g., the IT department) to establish a data-use agreement. This document must clarify how the data will be deidentified, transferred, and stored.
For this form of data, the critical privacy challenge might not be localization itself, but rather the aggregation of data over a period of time [56]. Data spanning a longer period are more susceptible to cross-analyzing and identifying. To mitigate over-accumulation of data, we suggest an adherence to principles of data minimization [36]. Instead of storing entire mobility graphs, the campus can compute and preserve only high-level insights, such as the importance of locations. This redacts any underlying individual behavior and corresponding identifiable information. Actually, for future purposes campuses can consider a form of differential privacy that authorizes limited forms of data querying depending on the privileges of the stakeholder [4].
An operational application would require the university to update the terms of use for its managed network. Particularly, the university should disclose how this data can be used in critical circumstances that invoke shared vulnerabilities [7]. On notifying the campus community of this change it offers individuals the choice to refrain from using the university network. Prior work on a sample within the same university campus shows that 90% of students are connected to the network on any given day [13]. Therefore, proposing such an opt-out condition can be viewed as an unfair choice. As a result, the campus needs to develop a contingency plan to accommodate network access to users who do not want their mobility behavior to constitute the aggregated insights.
Limitations and Future Work
This work presents evidence that university campuses can repurpose existing data sources to inform the design of LC policies that can control COVID-19. We evaluate these policies as alternatives to other data-driven, but, broad impact policies that universities consider implementing, such as moving large classes online. One of the drawbacks of this analysis, however, is that it assumes all edges to be the same. For example, when constraining by mobility, in real scenarios losing certain visits might be more valuable than others. Decline in mobility around profit-making services, such as shops and cafeterias, versus losing mobility at common rooms have a different tangible effects on campus. Currently we take an agnostic stance towards the mobility behavior, where all visits at all locations are the same. In reality, implementing policies could have inequitable qualitative impacts despite appearing to have similar network configuration. This can be improved by embedding more qualitative information into the network and conceiving ingenious ways to associate costs to edges.
Similar to the assumption that all visits and locations, the current work also assumes all people to be equal. However, different people have different underlying conditions that can make their vulnerabilities more concerning [43]. The privacy safeguards of this study restricted the research team from acquiring any additional demographic or historical information. Further work can attempt to characterize the nodes by randomly seeding the network to reflect the approximate demographic break up of the community. Alternatively, researchers could try to estimate some demographic based on behavior as well. However, to leverage accurate individual information, even for operational use during a public health emergency, policymakers and researchers need to develop new privacy protocols [28].
Lastly, this paper only studies three rudimentary scenarios, persistence, non-residential avoidance, complete avoidance. These scenarios assume that when a location is shutdown, the individuals who ought to have visited that location do not come into contact with anyone else during the same time. Yet, other substitution behaviors are possible and the richness of networks leveraged with WiMob enables the exploration of various new scenarios that can be triggered by policy interventions on campus. For instance, individuals might not even visit transitory spaces, such as lobbies or cafes between classes. Certain collocations could be the consequence of social ties which might never be developed because of a shutdown (e.g., project teams meeting outside of class). Further research can illuminate the effects of policies in more specific scenarios by modeling post-intervention behavior more accurately.
Comparison of Contact Network Structure (Fall 2019)
Calibration outcomes with variations
Comparison of different LCPRank policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 - 4 in Fall 2020 at GT
Comparison of different LCBCen policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 - 4 in Fall 2020 at GT
Comparison of different LCECen policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 - 4 in Fall 2020 at GT
Comparison of different LCLCen policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 - 4 in Fall 2020 at GT
Comparison of different LCPRank policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 5 - 9 in Fall 2020 at GT
Comparison of different LCPRank policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 10 - 14 in Fall 2020 at GT
Comparison of different LCPRank policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 - 4 in Fall 2020 at UIUC
Comparison of different LCPrank policies in terms of controlling the disease and impacts on campus in Fall 2019; calibrated from week 0 – 4 in Fall 2020 at UC Berkeley
We calibrate ABM on positivity rates from Fall 2020 at GT. The objective function of the calibration is to minimize the r.m.s.e. with the weeekly average of positivity rate obtained from surveillance testing results at GT [25]. (a) The parameter that determines external transmission of infections on a given day, Iout(t), is a function of cases in Fulton county (where GT is located). (b) The models discussed in the main paper are calibrated using the first 5 weeks of data. We illustrate the output for a range of parameters that incorporate quantitative uncertainty, i.e., within 40% of the r.m.s.e. (c, d) illustrate calibration on the second period of 5 weeks and third period of 5 weeks respectively. These only show the optimal parameter output. The shaded region around the lines show the 2.5th and 97.5th percentile.
We calibrate ABM on positivity rates from first 5 weeks of Fall 2020 at UIUC. The objective function of the calibration is to minimize the r.m.s.e. with the weekly average of positivity rate obtained from surveillance testing results at GT [25]. (a) The parameter that determines external transmission of infections on a given day, Iout(t), is a function of cases in Champaign county (where UIUC is located). (b) We illustrate the output for a range of parameters that incorporate quantitative uncertainty, i.e., within 40% of the r.m.s.e. The shaded region around the lines show the 2.5th and 97.5th percentile.
We calibrate ABM on positivity rates from first 5 weeks of Fall 2020 at UC Berkeley. The objective function of the calibration is to minimize the r.m.s.e. with the weekly average of positivity rate obtained from surveillance testing results at GT [25]. (a) The parameter that determines external transmission of infections on a given day, Iout(t), is a function of cases in Alameda county (where UIUC is located). (b) We illustrate the output for a range of parameters that incorporate quantitative uncertainty, i.e., within 40% of the r.m.s.e. The shaded region around the lines show the 2.5th and 97.5th percentile.
Disease control outcomes in Fall 2019 for different algorithms of LC with the ABM is calibrated on weeks 0 - 4 of Fall 2020 at GT. (a - c) Comparison of RI with LCPRank. Under all scenarios, for peak infection reduction (b) and internal transmission reduction (c), LCPRank shows better disease control outcomes than RI. For total infection reduction (b), LCPRank is better in S1, worse in S3 when designed within an exposure risk budget, and comparable in others. (d - f) Comparison of RI with LCBCen. Under all scenarios, for peak infection reduction (d) and internal transmission reduction (f) LCBCen is better when designed within an exposure risk budget. For total infection reduction (e), LCBCen is always worse than RI
Disease control outcomes in Fall 2019 for different algorithms of LC with the ABM is calibrated on weeks 0 - 4 of Fall 2020 at GT. (a - c) Comparison of RI with LCECen. Under all scenarios, for peak infection reduction (b) and internal transmission reduction (c), LCECen shows better disease control outcomes than RI. For total infection reduction (b), LCECen is better in S1 and worse in S3 when designed within an exposure risk budget. (d-f) Comparison of RI with LCECen. Under all scenarios, for peak infection reduction (d) and internal transmission reduction (f), LCECen shows better disease control outcomes than RI. For total infection reduction (e), LCECen is better in S1 and worse in S3 when designed within an exposure risk budget.
Disease control outcomes in Fall 2019 for LCPRank. (a - c) The ABM was calibrated on weeks 5 - 9 of Fall 2020 at GT. Under all scenarios, for all outcomes, LCPRank is better than RI. (d - f) The ABM was calibrated on weeks 10 - 14 of Fall 2020 at GT. Under all scenarios, for all outcomes, LCPRank is better than RI.
Disease control outcomes in Fall 2019 for LCPRank. (a - c) The ABM was calibrated on weeks 0 - 4 of Fall 2020 at UIUC. Under all scenarios, for all outcomes, LCPRank is better than RI. (d - f) The ABM was calibrated on weeks 0 - 4 of Fall 2020 at UC Berkeley. Under all scenarios, for all outcomes, LCPRank is better than RI.
Cumulative infections in Fall 2019 while comparing RI and LCPRank with ABM calibrated on weeks 0 - 4 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no- intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCPRank in comparison to RI. (g - i) External transmissions are higher with LCPRank in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCBCen with ABM calibrated on weeks 0 - 4 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no-intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCBCen in comparison to RI, only when constrained under the exposure risk budget. (g - i) External transmissions are higher with LCBCen in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCECen with ABM calibrated on weeks 0 - 4 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no- intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCECen in comparison to RI. (g - i) External transmissions are higher with LCECen in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCLCen with ABM calibrated on weeks 0 - 4 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no- intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCLCen in comparison to RI. (g - i) External transmissions are higher with LCLCen in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCPRank with ABM calibrated on weeks 5 − 9 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a − c) Total infections of interventions is lower than nointervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d − f) Internal transmissions are lower with LCPRank in comparison to RI. (g − i) External transmissions are higher with LCPRank in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCPRank with ABM calibrated on weeks 10 − 14 of Fall 2020, GT. The bands show the 2.75th and 97.25th percentile. (a − c) Total infections of interventions is lower than nointervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d − f) Internal transmissions are lower with LCPRank in comparison to RI. (g − i) External transmissions are higher with LCPrank in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCPRank with ABM calibrated on weeks 0 - 4 of Fall 2020, UIUC. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no-intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCPRank in comparison to RI. (g - i) External transmissions are higher with LCPRank in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
Cumulative infections in Fall 2019 while comparing RI and LCPRank with ABM calibrated on weeks 0 - 4 of Fall 2020, UC Berkeley. The bands show the 2.75th and 97.25th percentile. (a - c) Total infections of interventions is lower than no-intervention scenarios and is lowest in the S3 scenario. In this scenario, the mobility budget is 69% of what it would be without interventions, and therefore the transmissions are also contained. In comparison, in Fall 2020, we saw far fewer infections which is because the mobility was 39% of that in Fall 2019. (d - f) Internal transmissions are lower with LCPRank in comparison to RI. (g - i) External transmissions are higher with LCPRank in comparison to RI. Since internal transmission is controlled, more individuals remain susceptible to infections from outside campus.
The locations shutdown by each policy are grouped into the the general building category. The distribution of locations is different between policies, for example, in S1 (a) and S2 (b), LC closes fewer locations that RI. Even when targeting spaces in similar buildings, the locations are qualitatively different RI only affects classrooms, whereas LC also closes smaller spaces like breakout rooms, reading areas and cafes. LC In S3 (c) we find LC to target locations in a greater variety of buildings, but it also targets more locations to utilize the budget.
The locations shutdown by each policy are grouped into the the general building category. The distribution of locations is different between policies, for example, in S1 (a) and S2 (b), LC closes fewer locations that RI. Even when targeting spaces in similar buildings, the locations are qualitatively different RI only affects classrooms, whereas LC also closes smaller spaces like breakout rooms, reading areas and cafes. LC In S3 (c) we find LC to target locations in a greater variety of buildings, but it also targets more locations to utilize the budget.
SI References
Acknowledgements
This paper is based on work partially supported by the NSF (Expeditions CCF-1918770, CAREER IIS-2028586, RAPID IIS-2027862, RAPID IIS-2027689, Medium IIS-1955883, NRT DGE-1545362, CCF-2115126), CDC MInD program, ORNL, and Semiconductor Research Corporation (in collaboration with Intel Labs). Some research personnel were supported by internal seed funding from the Georgia Institute of Technology and Georgia Tech Research Institute. Other computing resources were provided by the Office of Information Technology at Georgia Tech. The authors thank Di Wu, Hanna Hamilton, and Dima Nazzal (Georgia Institute of Technology) for their analysis of En.
References
- [1].↵
- [2].↵
- [3].↵
- [4].↵
- [5].↵
- [6].↵
- [7].↵
- [8].↵
- [9].↵
- [10].↵
- [11].↵
- [12].↵
- [13].↵
- [14].↵
- [15].↵
- [16].↵
- [17].↵
- [18].↵
- [19].↵
- [20].↵
- [21].↵
- [22].↵
- [23].↵
- [24].↵
- [25].↵
- [26].↵
- [27].↵
- [28].↵
- [29].↵
- [30].↵
- [31].↵
- [32].↵
- [33].↵
- [34].↵
- [35].
- [36].↵
- [37].↵
- [38].↵
- [39].↵
- [40].↵
- [41].↵
- [42].↵
- [43].↵
- [44].↵
- [45].↵
- [46].↵
- [47].↵
- [48].↵
- [49].↵
- [50].↵
- [51].↵
- [52].↵
- [53].↵
- [54].↵
- [55].↵
- [56].↵
- [57].↵
- [58].↵
- [59].↵
- [60].↵
- [61].↵
- [62].↵
- [63].↵
- [64].↵
- [65].↵
- [66].↵
References from SI
