Abstract
We construct a compartmental individual-based model of Covid-19 infection spread. The model can be used to predict the infection trajectory in general environments with various interventions introduced. Tasked by the Welsh Government, we apply the model to secondary schools and Further and Higher Education environments. Specifically, we consider populations mixing in both a classroom and Halls of Residence. Our particular focus was to question the potential efficacy of Lateral Flow Devices (LFDs) when used in broad-based screens for asymptomatic infection or in ‘test-to-release’ contexts in which individuals who have been exposed to infection are released from isolation. To compare scales of efficacy LFDs are compared to other non-pharmacological interventions. We find that, although tests can be used to reduce disease incidence, investments in personal protective equipment (e.g. masks) and increasing ventilation quality in enclosed environments is more effective in lowering disease prevalence.
1 Introduction
When the Covid-19 pandemic swept across the globe [1, 2, 3], governments tried to stem infection by imposing national lockdowns in which services, such as education, were shut, or moved online [4]. Following successive epidemic waves there have been extensive efforts to get students, across all age ranges, back into schools, colleges and universities [5, 6, 7, 8]. Primarily, the arguments have focused on the benefits of education for the development of skills, knowledge and maintenance of good mental health [9, 10, 11, 12].
There has been a vigorous debate about the role of schools and universities in disease transmission and, as such, the use of a range of non-pharmacological interventions (NPIs) have been proposed and utilised in the education sector [13, 14, 15]. In the UK, there is currently a focus on using Lateral Flow Devices (LFDs) as a means of detecting infected individuals to better manage infection [16, 17, 18]. Controversially, it has been suggested that a negative result from an LFD might be used to release people who, following a close contact with an infected individual, had been advised to self-isolate [19, 20, 21]. Critically, LFDs have a high false negative rate [22], thus we investigated how beneficial they would be in relation to other NPIs, particularly in a landscape of vaccine rollout where personal adherence with contact and isolation policies may be in decline [23].
Mathematical modelling offers a wide variety of techniques to predict the impact of interventions on infection spread without risking anyone’s health [24]. Notably, many different mathematical fields are able to provide predictive results, for example we could use deterministic and stochastic differential equations [25], machine learning [26], Monte Carlo simulation [27] and queuing theory [28]. For the small number of individuals we are considering in our simulations a deterministic approach would not be justified [29]. Further, the machine learning tools, or continuous time data techniques [30], are not currently viable, due to a lack of data. Though infection modelling and analysis has been conducted on the impact of school reopening on local R numbers [31], what we lack is a way of tracking infection spread through multiple linked spatial compartments that is flexible enough to include a variety of NPIs. Our contribution is to generate an individual-based model of infection spread that splits the susceptible population into local and nonlocal groups. The algorithm can be used to predict the development of an infection in many situations, where individuals naturally form groups, or cliques. We focus on modelling the educational setting, namely, we seek to predict how testing, isolation and other interventions influence the spread of infection in secondary schools, Further Education (FE) settings (e.g. colleges) and Higher Education (HE) settings, (e.g. Halls of Residence in a university). Importantly, the local versus nonlocal distinction can be used to differentiate between short-range droplet and longer-range aerosol mechanisms of transmission [32].
Our results are based on current UK data, however, we provide the reader with links to a maintained repository of open source MATLAB code (see Section 2.4) that not only reproduces our results, but can also be adapted by the reader to include data which is more accurate and/or specific to their location and needs.
Our results have been presented to TAG (Technical Advisory Group for Welsh Government Covid-19 response) and the Wales Further and Higher Education Covid-19 Task Group. It is currently being used to inform policy in relation to the future of students returning to educational environments. Further, our findings presented here have been shared with the Environmental Science Subgroup for use in advising how to open up more general social spaces, such as places of worship. The data has been communicated across the governments of England, Scotland and Northern Ireland, and has informed the wider development of policy planning.
Section 2 presents the assumptions and processes that underlie the algorithm that controls the individual agents (aggregations of pupils, students, etc.) that we are simulating. Specifically, we clarify how testing and agent isolation is enacted in sections 2.2 and 2.3. The algorithm is then run in Section 3 across two situations: (i) a secondary school/FE environment, Section 3.1, and (ii) a Halls of Residence at a Higher Education establishment, Section 3.2. Critically, within each of these broad applications we consider the effects of how and when testing is applied. Finally, in Section 4 we condense our findings down to simple observations which summarise our findings regarding the applications of LFD versus other possible interventions.
2 Computational framework
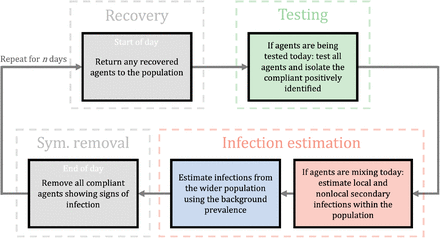
We have constructed an individual-based stochastic simulation of infection spread. The code is comprised of different modules that can be turned on, or off, as appropriate, so that the simulation can match a variety of policy situations. For example, we can vary the days and ways in which testing is conducted. We provide a basic description of the ideas behind the algorithm here with an overview illustrated in Figure 1. A descriptive flowchart of the algorithm is provided in Appendix A.
A flowchart illustrating the general iterative process controlling the dynamics of the discrete population over a typical day post simulation initialisation. Grey boxes represent actions that occur every day whereas as the coloured boxes can be independently active/ inactive on any prescribed day. A single cycle accounts for a single day. We start each day at the recovery box which returns any isolating agents that have completed their isolation period. If testing is active, the individuals are tested using LFD, agents with a positive test are removed from the population for tr days. If agents are allowed to mix, then we estimate secondary infections using R with context specific scalings (e.g. NPIs). Next, if external infection sources are being considered, we estimate the number of infections to the susceptible population using the background prevalence. Finally, we remove any compliant symptomatic individuals that display the infection at the end of every day. For a detailed flowchart of the infection algorithm, see Appendix A.
We consider a population of N susceptible individuals split into groups of size Ng, where 1 ≤ Ng ≤ N. Currently, Ng must be an integer factor of N. The parameter Ng is the number of local contacts an individual has and represents the number of isolations that would occur should a member of a group become identified as infectious. Specifically, if Ng = 1 only an infected individual is isolated upon (i) becoming symptomatic, or (ii) receiving a positive LFD test. Whereas, if Ng = N the entire simulated population is isolated upon the identification of an infected individual. Finally, if Ng is any other divisor of N then only a subgroup of the population is isolated upon the identification of an infected individual. As we consider different educational settings we will ascribe different definitions to Ng. Namely, in a primary/ junior/ secondary/ FE school setting Ng will represent a ‘table group’. These are individuals who are socially distanced to current regulations, but are sat on the same table. This is in contrast to the HE case where we consider Ng to be the size of a ‘kitchen group’. These are individuals in shared accommodation that share the same facilities.
Critically, the effectiveness of isolation is modulated by a ‘compliance parameter’, C. In the secondary school setting we assume that the school is keeping records of positive tests and has a final say on who is allowed to enter the classroom. Thus, we assume that C = 100% and, thus, any student that is symptomatic, or receives a positive test results, is isolated completely and cannot pass on further infections to the simulated population.
The secondary school situation stands in contrast to the FE and HE cases, where information supplied by the Welsh Government’s Head of Policy HE Covid-19 (B. Cradock, 4th Feb 2021, pers. comm.) suggests that students in the HE environment are only 81% likely to comply with an isolation order. Hence, in such cases, after receiving a positive test result, or becoming symptomatic, a FE, or HE student is only isolated with a probability specified by the parameter C.
As discussed above the code accounts for both symptomatic and asymptomatic individuals. Specifically, the percentage of symptomatic individuals is defined as Ps. At the point of infection each individual is either given a symptomatic, or an asymptomatic flag based on this percentage. Asymptomatic individuals are able to infect other susceptible individuals but will not isolate unless tested, whereas symptomatic individuals are assumed to follow public health guidance and follow self-isolation guidance at a rate determined by the compliance parameter. Symptomatic individuals who choose not to be tested are treated as asymptomatic. A non-exhaustive list of real-world infection events and model interpretation is supplied in Table 2 in Appendix A.
A table representing real-world infection events as interpreted by the model framework presented in this study.
The explicit timescale of the algorithm is assumed to be a day. Namely, for every day we specify whether individuals are to be tested and whether they are able to mix. These scenarios are independent and, thus, we control whether neither, one, or both scenarios occur. For example, because we are modelling a school, or college location, we currently specify that secondary and FE students do not mix on a weekend and, equally, no testing happens on a weekend. Whereas in the Halls of Residence setting of the HE simulations mixing and testing can occur every day.
As seen at the beginning of the flow diagram in Figure 1, during any day that testing is applied all individuals that are not isolating are tested. The testing phase occurs before the mixing phase. Thus, any individual triggering a positive result is isolated before they can infect others. Critically, we currently do not include infection transmission once individuals are isolating as we suspend any isolating agent from the simulation for td days. Specifically, in a secondary school, if the whole class is isolating no further infections appear. This assumption is reasonable in the secondary and FE cases as the students are physically isolated from one another. However, in the HE case, further infections may occur within isolated flats. Thus, when we compare the isolating individuals across those that are infected and those that are not we only quote this ratio to be correct at the point of isolation, because, as mentioned, further infections within an isolating subgroup are not tracked but are likely to occur, see Section 4.2.
Due to the algorithm being able to contend with subgroups within a population we have effectively added two compartment spatial complexity to the infection model. Namely those within a group are considered ‘local’ contacts and those outside of a group are considered ‘nonlocal’ contacts. Because of this addition of spatial complexity, the basic reproduction number, R is split into two R numbers:
a local number, Rl, that measures the expected number of secondary infections within a subgroup that has an infected person; and
a nonlocal number, Rn, that measures the expected number of secondary infections that occur due to infectious people in other subgroups.
Critically, the basic reproduction number, R, can be estimated from data and Rl and Rn are defined such that R = Rl + Rn. Specifically, we define a ratio of local to nonlocal infections, cl : cn, and, thus, Rl = clR/(cl + cn) and Rn = cnR/(cl + cn).
Defining the local to nonlocal infection ratio, cl : cn, depends on how we assume the virus spreads. For example, in a secondary school environment, if there is a lot of movement within a classroom and intergroup mixing then we might expect there to be no difference between the number of infections within groups to infections between groups, in which case cl = cn. However, if a good social distancing policy is implemented, we would expect the number of nonlocal infections to be lower than the number of local infections, i.e. cn < cl.
Explicitly, for the secondary school simulations, we are choosing to inform Rl and Rn through the steady state level of spread of airborne particles [33]. Specifically, we define cl to be the local concentration, which is the contagion concentration 2 metres distant from an infected individual. This represents the worst-case scenario for the amount of contagion that a susceptible person would receive if there was an infected individual in their subgroup. Further, we define cn to be the nonlocal concentration, which is the contagion concentration 4 metres distance from an infected individual. This represents the mean average scenario for the amount of contagion that a susceptible person would receive if there was an infected individual in another subgroup. Note that here the ratio cl : cn is fixed, with the values taken from the airborne simulations at 5 hours, which is consistent with the day time scale, on which we are working. However, this ratio should actually be evolving as predicted by [33].
In the HE case, where we consider the infection spreading through a Halls of Residence we choose to define this ratio based on the compliance of the individuals to social distancing rules. Specifically, we consider two cases. The first is the ‘poor social distancing’ where residents from all flats mix, i.e., the local and nonlocal infection numbers are equal (cl : cn is 1:1, or Rl = Rn). The second case considers ‘enhanced social distancing’, where on average, 5 out of 6 flat residents are only socialising with members of their same flat, whilst 1 in every 6 people still mix with other flats even when strict social distancing measures have been advised. Thus, in the enhanced social distancing case, the ratio of local to nonlocal infections is 5 : 1. This value was estimated to agree approximately with the isolation compliance probability of C = 81%. However, we did not simply choose a ratio of 4 : 1, which would match this compliance, because the ratio of 5 : 1 is more interpretable when the flat occupancies are of size 6, or Namely, on average, there is one, or two, poorly compliant individuals in the flats, respectively.
Alternatively, instead of splitting R into local and nonlocal contributions there is the future possibility of using research focused on simulating airborne particle spread to specify Rl and Rn directly [33], thus providing a mechanistic way of understanding R. This could be encompassed into our simulation, but we would need to reduce the smallest discrete time unit within the model to be hours, rather than days.
We now consider the blue and red sections of Figure 1, which are the infection stages. The blue section controls external infections, namely infections that occur outside of a school, or Hall of Residence, as appropriate. In the secondary school scenario, we assume that these happen at the end of the day due to socialising after school, which is why the red section feeds into the blue section. These infections occur at the local prevalence rate, I [34] can be turned on, or off, depending how well we believe our system is isolated from the outside world. Equally, isolating the system allows us to consider how the systeminfluences itself under any intervention.
The red sections of Figure 1 control how secondary infections are generated due to mixing between individuals. During any day where the students can mix then any individual that is:
infected;
infectious; and
not isolated
can infect other people. Once a person becomes infected three delay clocks are attached to each of them. The three delays [35], ti, td and tr, represent:
the time between becoming infected to becoming infectious, ti =3 days;
the time between becoming infected to becoming detectable by a LFD test, td = 5 days; and
the time between becoming infected to recovery, tr = 10 days.
Any recovered person is assumed to be non-infectious and immune to further infections. Currently, these delays are fixed, but these could easily be made variable. Note that the recovery and isolation timescales are independent. Thus, once an individual is discovered to be infected they are isolated for 10 further days, no matter where they are within the infection timeline. For example, if an individual is found on the 9th day of their infection they have to isolate for another 10 days, even though they would recover the next day.
Finally, we assume that the tests being used are Lateral Flow Devices, LFD, which are assigned to have a false positive probability, Pfp and a false negative probability of Pfn. Throughout the simulations, we will vary Pfn but keep the false positive probability fixed to Pfp = 0.003, in agreement with existing LFD studies [19, 22, 36].
2.1 Interventions
Since we are assuming that infections are mainly spread through airborne transmission. The epidemiological R value can be modified by additional interventions, i.e., masks and ventilation. Current research suggests that masks halve the R value, whilst ventilation yields a 5-fold decrease in R. The combined influence of masks and ventilation is multiplicative, namely R is reduced 10-fold [33].
Good ventilation also influences the local to nonlocal infection ratio. Specifically, in classroom scenarios, under suboptimal ventilation conditions we fix cl = 1 and cn = 1/2. Namely, you are twice as likely to be infected when you are close to an infected individual than when you are far away. However, good ventilation conditions change this ratio to 1:1/9.
Thus, good ventilation impacts on the simulation in two ways. Firstly, good ventilation reduces the contagion in the air, thereby lowering the R value. Secondly, the ventilation reduces the spread of the contagion beyond a table group, meaning the infections are more likely to be localised and thus, causing cl to increase relative to cf.
In the Halls of Residence scenarios we cannot easily influence the ventilation capabilities of a flat. Further, masks will not be worn whilst the individuals are in their own flats. Thus, we consider the interventions to be enacted through guidance from the university about reducing the number of nonlocal contacts an individual has. Specifically, as mentioned above, we do not influence R, but rather the ratio of local to nonlocal infections. In the ‘poor social distancing’ scenario residents from all flats mix and, thus, the local and nonlocal infection numbers are equal, cl : cn is 1:1. In the ‘enhanced social distancing’ scenario individuals are encouraged to isolate as much as possible, but, more likely, socialise only within their kitchen group. This reduces the nonlocal infections, compared to the local infection, and, thus, we take the ratio cl : cn to be 1:1/5, for reasons stated in Section 2.
2.2 Testing regimes
Alongside varying the false negative probability of the LFD we consider a variety of different testing and isolation scenarios. The base case against which we compare all other cases is the no testing and no isolation of contacts case. Namely, the disease is simply allowed to spread through a class, or Halls of Residence without impedance.
Noting that in the cases modelled, only non-isolating individuals use LFD devices we can alter the testing regime for the population from weekly to daily. Further, we can alter the event that causes testing to occur. Either testing occurs on a fixed regime, or alternatively, no testing is applied until a first symptomatic person is found, that is, there exists an agent showing symptoms that day. Once a symptomatic individual is found, testing is applied through a weekly, or daily regime.
Other “reactive” testing regimes can be included (e.g., you always test after a symptomatic is found, rather than just moving to a fixed regime), but the “no testing” to “daily testing” range provides the extreme limits in which all other possible testing scenarios must fall. In Section 3 we will see that these extreme testing scenarios provide limits over a small range of results and, thus, all other proposed testing regimes must fit within these limits. Hence, understanding only the limiting cases provides us with enough knowledge to understand all cases.
As a specific example, in the secondary school case, we are particularly interested in the case of “test-to-release”. Namely, it was previously the case that if an infected individual was found then their close contacts would be isolated too, in this case this would be their table group (see Figure 2(c)). However, current guidance [5, 6, 7] is that a negative LFD result could release individuals in the table group that test negatively. Under our simulation this would conform to the individual isolation case. Namely, only the individual is forced to isolate, whilst everyone else is tested before they are then allowed to mix (see Figure 2(b)).
Mean number of infected students and average number of days absent per individual when no testing is employed, over a variety of isolation strategies and interventions in a secondary school environment. Each symbol represents a different intervention, see legend at the top of the figure for details and see Section 2.1 for a description of how each intervention influences the parameter values.Note that the 4 pie charts in (b) have visually small sectors representing isolation of healthy individuals with a false-positive test result.
In the HE setting we compare the efficacy of the various testing strategies at two time points during a term. In the first scenario, called the ‘start of term’ scenario, the first simulated week occurs prior to students returning to the Halls of Residence. In this initial week students do not mix, but any infected student will incubate their infection. The next three weeks are simulated under the assumption that the students are back in their halls and able to mix daily. The second scenario, called the ‘middle of term’ scenario, considers a period post student arrival, where the individuals are mixing each day (including weekends) for four weeks.
2.3 Isolation regimes
As mentioned in Section 2.2 we initially consider the case in which no isolation occurs. This situation can then be compared against:
isolating individuals due to the individual being symptomatic, or receiving a positive test result;
isolating subgroups due to at least one individual in the subgroup being symptomatic, or receiving a positive test result;
isolating an entire population due to at least one individual being symptomatic, or receiving a positive test result;
Note that the positive test results leading to an isolation can be either true or false positives.
Throughout the simulation we keep track of the number of people who are isolating. Further, the scatter points illustrated in Section 3 are all pie charts that represent the ratio of infected people who are isolating (white part of the pie chart) versus the number of people who are isolating, but healthy (colour part of the pie chart).
2.4 Code availability and parameter values
To elucidate the robustness of the LFD testing strategies in various infectious environments, we simulate the mathematical model across a variety of parameter values. A best-case scenario would be when there is: a low background prevalence; a low R number, and a low probability of false negatives, Pfn. In contrast, the situation becomes worse when any of these parameters are increased. For each parameter we choose two extreme values (see Table 1) and simulate over all combinations of these values. In addition to these global parameters, we provide a summary of context specific parameter values and parameter definitions in tables 3 and 4 in Appendix A. Note that the R number, as referenced in tables 1 and 4, is the local background R number, that is parameterised using the National R number estimates for our best- and worst-case scenarios [37]. The actual numbers that apply in School or University environments are anticipated to lie between these extremes and may depend on whether transmission between children, adolescents and young adults differ substantially from aggregate National R numbers [38]. Clearly local strategies such as increasing ventilation or mandating mask use may already contribute to the lower estimate of the National R number. Nonetheless, we anticipate that the modelled NPIs will apply between the two R numbers suggested.
Table of parameter values used in all education environments simulations.
A summary of parameter values used for secondary school and HE simulations. See Section 2.2 for information on various testing regimes.
A table of model parameters with their associated definitions.
Our intention is to illustrate our code in a number of educational settings, but our algorithm can be used to predict infection numbers across variety of other locations. Equally, we provide one interpretation of how interventions influence the outcome. The actions and interpretations of the interventions are completely arbitrary and, thus, the algorithm can be exploited to provide predictive results including a new variety of interventions, so long as the user has a clear idea how the interventions influence the input parameters.
Moreover, our interest is to investigate a wide space of reasonable parameter values to illustrate how diverse our results can be. As parameter estimates become better over time, due to more data being collected, we may want to return to our simulations and run the computation under specific parameter values that represent our current knowledge of a system. Alternatively, in line with the above comments about extending the interpretation of our code, the parameters will also have to be reinterpreted within the new scenarios.
To account for this diversity of use we provide open access to our code, which is stored and maintained at http://bit.ly/LFD_IBM_Repo. The code has been run and tested on MATLAB 2020B. We hope that releasing our code allows other to expedite their response to the pandemic through predicting which of their intervention options is the best.
3 Results
The algorithm is able to output an immense amount of data. Specifically, we track the infection, isolation and symptomatic status of every individual with a day-time resolution. Further, due to the stochastic nature of the algorithm, the code is run 1000 times for each scenario, which provides us with an under-standing of the sensitivity of our estimates. Thus, although many daily statistics are available as outputs from the code, we visualise only the average total number of infections versus the average number of days isolating per individual.
Note that the speed of the simulations is mainly determined by the size of N, since we fix the number of repetitions. Thus, for the FE classes, which are of size N = 10, 1000 simulations takes approximately 9.9 seconds to complete. However, in the case of the Halls of Residence, where N = 204 the results take approximately 40.3 seconds1. Sweeping over the 5-dimensional parameter space required to analyse the best and worst-case scenarios, simulation times scale linearly, achieving a maximum simulation time of approximately 4 hours to complete in the HE settings.
As mentioned in Section 2.3 we present a number of Figures that use pie charts to track numbers of infected or healthy individuals isolating at points that are scattered in the space of average ‘infections’ versus ‘days of isolation per individual’. Each pie chart represents a different intervention. The intervention is encoded in the colour and transparency of the pie chart. The coloured part of each pie chart represents the proportion of ‘correct’ isolations, i.e. isolations of infected people, whereas the white section represents the proportion of incorrect isolations, i.e. isolations of healthy people. Thus, when seeking to optimise NPIs, we may independently assess overall infection rates and approaches that minimise the isolation of uninfected individuals.
Overall, we assume policy makers are primarily interested in minimizing the total number of infections and the number of days spent in isolation. Thus, we look to strategies that produce points near to the origin, (0,0) with the lowest proportion of uninfected individuals isolating (coloured section of pie charts). When these two goals are in conflict, it would be assumed that minimising the total number of infections would have priority.
3.1 Secondary school environments
In this case we set the class size to be N = 30 and consider Ng = 1, 5 and 30. Thus, apart from the case where no isolation occurs, we will either be isolating: only an infected individual, an infected and their table group, or the entire class, respectively (see Table 2 for our interpretation of real-world events in the modelling framework).
As a base case for investigating the efficacy of testing we, first, run the model without testing included. Thus, the parameter Pfn is irrelevant. Thus we focus on varying the level of symptomatic prevalence, Ps between 20% and 50%. Having a large population of asymptomatics, potentially causes problems when we run a reactive testing strategy, rather than a fixed testing strategy (see Section 3.1.2) [39, 40]. When testing is considered, we fix Ps = 20%, which provides the worst-case scenario of 80% of the infected population not presenting symptoms.
Equally, from simulating all combinations of the best- and worst-case parameters as discussed in Table 1 we note that reducing R reduces the average total number of infected people and the average number of days isolation better than reducing the false negative probability, Pfn. Noting that this observation remains true over all simulations we suppress the data from mixed simulation for clarity of discussion and only present the best- and worst-case parameter values.
The simulations are run over 28 days and we assume that the simulation starts on a Sunday, see Figure 6 for an explicit description of simulation initialisation. Defining the starting day is important as we assume that testing and mixing can only occur during weekdays, not weekends.
Flowchart illustrating the algorithm developed for the individual based model of infection spread. We highlight various subroutines using colours: grey is base infection routines, green is testing, red is secondary infection estimation and blue represents infections from outside the population. SI corresponds to secondary infections.
In the context of a secondary school, the Head Teacher has the authority to remove any student displaying symptoms from the classroom. In addition, as the school will oversee testing and recording of results, we set the percentage of student compliance to 100%. From data not shown, we note that varying compliance and background infection rates, within realistic limits, (i.e., 60 ≤ C ≤ 100 and 0.5 ≤ I ≤ 2) does not significantly influence the forthcoming insights, thus, we have suppressed this output. Reducing the local prevalence rate I to 0.5% from 2% has an insignificant effect on the number of infections within the classroom due to the population size being small (N = 30). Namely, we would have required at least a prevalence rate of I = 3.3% to infect at least one student per simulation by wider population transmission. Although changing the compliance has the obvious influence on the quantitative results the qualitative results remain the same from the perspective of intervention efficacy. Hence, in the following figures all simulations have a background infection prevalence of I = 2% and a compliance of C = 100%.
3.1.1 Without testing
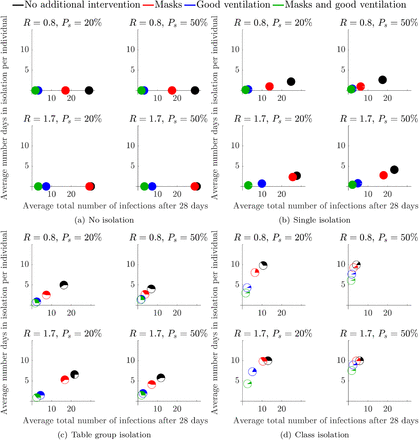
Figure 2 presents the simulations under the assumption of no LFD testing. Thus, in the cases where isolations occur, isolations are only able to occur when a student becomes symptomatic (3 days post infection) and/or when those who have been exposed to possible infection are asked to isolate.
Figure 2(a) presents the worst-case scenario where individuals are exposed to a presymptomatic infectious individual under circumstances when school contacts are not isolated. Thus, if there are no interventions then eventually everyone becomes infected within a four-week period (i.e. the black pie chart is always at 30 on the x-axis). Note that, since there are no isolations, we have not isolated any healthy people, thus, the pie charts are fully coloured. Equally, due to having no isolations, even from students showing symptoms, there are no absences, thus, all pie charts lie on the x-axis. In Figure 2(b) only the single symptomatic infected individual isolates, whereas in figures 2(c) and 2(d) the school has been notified and either the table group, or entire class, respectively, has been asked to isolate, as well.
We note from Figure 2(a), which is true over all subfigures and subplots that the level of intervention is increased fewer people become infected. Moreover, although having both masks and ventilation is the best policy, increased ventilation is the better single intervention, because of the double impact of localising the infections, as well as removing the particles from the air. This is seen through noting that the green and blue pie charts are much more left in all cases than the red and black pie charts.
Comparing columns and rows in each subfigure shows that increasing R increases the average number of infected individuals as expected. An increase in the percentage of individuals who display symptoms (Ps) reduces the total number of infected people symptomatic individuals self-isolate (compare figures 2(a) and 2(b)). As an indirect consequence, a reduced number of infections feeds through into a lower average number of days in isolation per individual (Figure 2(b)). A reduction in R similarly leads to a reduction in both infection and isolation metrics.Critically, although influencing both parameters is beneficial for our purposes, we are unable to physically influence Ps as this is an intrinsic property of the infection. Noting that these observations of altering R and Ps remains true over all simulations then in future figures we only focus on simulations where R is varied as this is the parameter that NPIs can influence.
Another result that is consistent across all our simulations and across the secondary, FE and HE scenarios is that isolating larger subgroups of the population is one of the surest ways of reducing the average total number of infections. The contribution of contact isolation becomes greater when good ventilation and mask use is not in place. However, this strategy increases both the number of days in isolation and the number of healthy individuals isolating. Specifically, as the isolation group size is increased from the individual, to the table group and, finally, to the entire class (figures 2(b)-2(d), respectively) the pie charts move left, up and the white sector becomes larger.
3.1.2 With testing
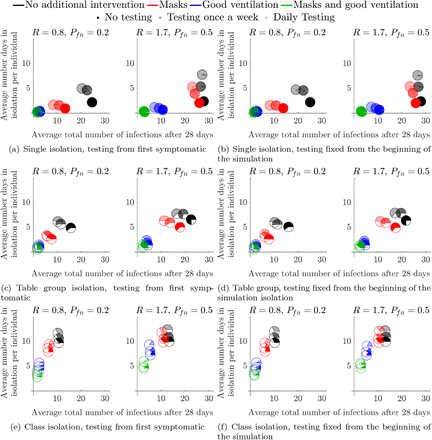
Figure 3 represents the same intervention strategies as those shown in Figure 2, however, we consider multiple testing scenarios. As mentioned, testing frequency is denoted by pie chart transparency. Namely, as the testing frequency is increased the pie charts become more transparent. Note that the no testing data from Figure 2 has also been included as the opaque pie charts, to allow for comparison against the base case.
Mean number of infected students and average number of days absent per individual when testing is employed, over a variety of isolation strategies and interventions in a secondary school environment. Each symbol represents a different intervention, see legend at the top of the figure for details and see Section 2.1 for a description of how each intervention influences the parameter values.
The simulations appearing in the left column of Figure 3 all assume that testing only occurs after a first symptomatic individual appears (“reactive” testing), whereas the right column has a fixed testing strategy from the beginning of the simulation. Clearly, the outcome difference between these two strategies is minimal, although they may not differ for cost of implementation. The reason is that, even at a symptomatic (to asymptomatic) prevalence of 20%, a symptomatic individual is generated extremely quickly through secondary infections, which cause the testing strategies to begin almost as soon as the fixed strategies (random testing for asymptomatic students).
The overall trends mentioned in Figure 2 remain the same when comparing the different levels of testing, namely: reducing R is the best way of reducing further infections; ventilation is better than masks; and isolating more people greatly reduces the overall number of infections but increases the number of absences and the number of healthy people being isolated.
Notably, we see that the addition of weekly, or daily tests does reduce the number of overall infections, but more tests lead to more absences as more cases are found earlier in the infection cycle (the pie charts move left and up as they become more transparent). Critically, although testing does help, we see that reducing R is much more important, particularly due to the time-lag between being infectious and being detectable by LFD (td > ti) and so testing will never be able to fully remove infections from the population under our assumptions. As a result, simply wearing a mask and having no testing is as good as daily testing without a mask (the opaque red pie chart is always lower and left of the most transparent black pie chart).
When considering ‘test-to-release’ strategies, we note that infection rates were lower when pupils are asked to isolate if they have been in contact with infected individuals. Namely, in Figure 3(e) where R = 1.7 and Pfn = 0.5, the black, red, blue and green rates (solid colour; no testing) at 14, 10, 7 and 4 respectively. By contrast the equivalent numbers for pupils who are tested and released back to the School Population in a ‘test-to-release’ strategy (in Figure 3(a) R = 1.7 and Pfn = 0.5, the black, red, blue and green rates (transparent colour; daily testing) are 28, 26, 11 and 3. This would suggest that, if the primary policy goal was to minimise infections, that test-to-release would increase infections by comparison with either the table-isolation or whole-class isolation strategies.
3.2 Higher Education environments
The cohort size in this case is the population of a typical Halls of Residence, N = 204. These individuals are separated into flats, or ‘kitchen groups’ of size Ng = 6, or Ng = 12. We fix the symptomatic prevalence to be Ps = 40% and the compliance to be C = 81%.
Here, we mainly focus on trying to understand the influence of the flat size on the results and timing of the test. Specifically, see Section 2.2, where we discuss the start of term and middle of term testing scenarios.
3.2.1 Start of term
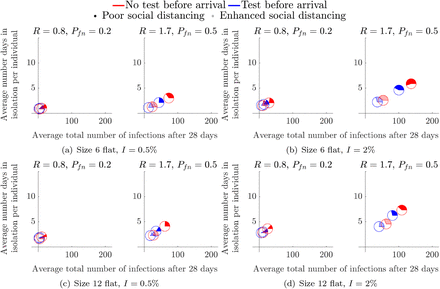
The start of term simulations starts a week prior to student mixing. Hence, all initially infected individuals are potentially detectable by the first administered LFD test in both strategies. Therefore, the lag time between being exposed to the virus, being infectious and being detectable has no effect on the initial transmission within the student population. In this scenario we consider the effect of a test prior to returning to the Halls of Residence. Namely, in Figure 4, the blue pie charts represent the case in which students are tested two days prior to arrival (Friday of week 1), followed by weekly tests, every Monday, starting on the day of arrival (Monday of week 2). The red pie charts represent the case where there is no test before returning. However, weekly tests are administered, every Monday, starting on the day of arrival (Monday of week 2), as in the blue pie chart case.
Considering the effects of a pre-term LFD test across flats of different occupancy (noted below each subfigure).
Figure 4 demonstrates that the addition of a test prior to arriving only has a significant benefit in high prevalence and high R number environments. The disparity in the total number of infections is particularly prominent in the cases of poor social distancing restrictions as the opaque pie charts are further apart (see figures 4(b) and 4(d)).
By comparing the results of Figure 4 across flat size, we observe that larger flat sizes result in a small decrease in average total number of infections, but a small increase in the average length of isolation period. Thus, although, a 12-person flat has an increased risk of someone bringing in an infection to the flat, once a positive test result occurs we remove more non-infected people from circulation. However, because we are only tracking infections to the point of isolation, we must be cautious regarding this interpretation. Specifically, once a flat has been isolated unless all remaining healthy individuals practice extremely good hygiene it is highly likely that most in the flat will succumb to the infection, meaning that the small reduction in total number of infections that is apparent in the results would not exist and in fact the larger flats would lead to a gain in average total of infections. Critically, this comes down to the responsibility of the individuals of an infected flat. Once a positive test has been received the flat should be clearly informed of their options and best practices that will keep the individuals safe.
In all cases we see that the coloured part of the pie chart is in the minority. Thus, at the point of isolation, we are isolating more healthy people than infected people. In particular, in larger flat sizes over 70% of all students isolating in every scenario are healthy in the 12-person flat simulations (see figures 4(c) and 4(d)). Though, it is not substantially less in the smaller 6-person flat, it is worth noting that increasing the flat size increases the number of healthy people isolating.
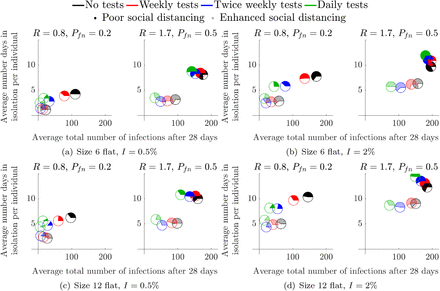
3.2.2. Middle of term
We next consider the situation where students have returned and are continuously mixing for a 28-day period. In every infection scenario we simulated, we show that increasing the testing frequency greatly reduces the total number of infections, i.e., the green and black pie charts are the closest and furthest markers from the origin, respectively, in all subplots of Figure 5. Further, in all subplots of Figure 5, we observe the benefit of including spatial compartments to the model by the restriction of social interactions from the whole population (opaque markers) to ‘kitchen groups’ (transparent markers), particularly in the cases of R = 1.7, as the spatial component of the model considers the allocation of infections between the infective’s group and rest of the student population (see Section 2). Critically, when the R number is large, we have a distinct disparity between the opaque and transparent markers, thus, enhanced social distancing measures reduces both the number of infections and days in isolation.
Considering the effects of a mid-term LFD test across flats of different occupancy (noted below each subfigure).
Critically, as in the secondary school case of Section 3.1, although testing is able to reduce the average total number of infected individuals it is much better to reduce the R value through encouraging enhanced social distancing measures. Specifically, in all cases, the transparent black pie chart is always closer to the origin than the green opaque pie chart.
Finally, our simulations suggest that increasing the flat size improves the efficacy of the enhanced social distancing measures, as all transparent pie charts are closer to the origin in the 12-person flats than their associated pie chart in the 6-person flat simulations. This observation is explained by the fact that increasing the size of a flat increases the number of healthy students that have to isolate when at least one infected student is found. Again, as mentioned in the previous section, we should critically examine this claim because unless the isolated individuals practice good hygiene the infection will spread through the isolating flat, thus generating more cases than expected. Future iterations of the model will contain this additional ability, see Section 4.2.
4 Discussion
Due to the time delay between becoming infectious and being detectable by a LFD [35], testing is never going to be able to stop infection spread, no matter how often it occurs. This would even be true in the case of PCR tests, which are more accurate (in terms of false negatives) and can produce results earlier in the incubation cycle. However, the time delay in obtaining results from RT-qPCR assays means that there may still be approximately one day between becoming infectious and becoming detectable. the only benefit would be a reduction in the proportion of false negatives (Pfn), which, as we have seen, is not an important parameter to focus on.
We have seen that testing can help reduce the total number of infections as LFDs enable us to find asymptomatic individuals, who would be able to spread the disease, even if they themselves do not suffer. Although testing as much as possible will help we must turn to alternative interventions if we want to have a significant impact on disease spread.
Here we have focused on several interventions across diverse educational contexts, both classrooms and Halls of Residence. Throughout all of our results we have seen that the simplest and cheapest way of reducing infection numbers is simply to isolate larger groups of individuals. At the extreme, isolating the entire population ensures that infections cannot be transmitted between individuals. Of course, such extreme solutions are unlikely to be desirable because we isolate many healthy individuals, whereby they miss educational and social aspects of everyday life [41]. Further, the ability to apply such a lockdown is impossible as “isolation fatigue” sets in and people’s compliance with harsh rules will likely diminish [42, 43].
Thus, how, when and who should be isolated are all important questions that should be carefully considered. Critically, isolating individual flats, classes or table groups hugely reduces the average total number of infections. However, this does not dictate total isolation, but encourages effective social distancing to limit infection spread.
We now look towards more proactive interventions that have a financial cost, namely: supplying personal protective equipment (e.g. masks); or investing in classroom sized ventilation units. Clearly, from the results of Section 3 we observe that the interventions we consider are always going to have positive influence on reducing disease transmission. Moreover, including multiple interventions offers bigger gains than each individual intervention. Based on the work of [33], we were able to show that although masks are a cheap and simple way of reducing disease spread, additional ventilation may be superior to masks in their ability to reduce the total number infections. Specifically, additional ventilation influences our simulations in two ways, firstly it reduces the amount of contagion in the air, thus, it reduces the number of secondary infections that can occur overall. Secondly, directed ventilation reduces the spread of transmission between spatially isolated population subgroups, thus, infected individuals are more localised, meaning that fewer people need to be isolated overall. Namely, with good room ventilation test-to-release becomes a viable option (see the blue pie charts in Figure 3). Specifically, even under worst-case parameter values, good ventilation means that we only need to isolate table groups to ensure the greatest reduction in total cases.
4.1 Impact
Our work has already helped to influence Welsh Government policy in relation to the development of FE and HE workplace and residential policy. Our model was used to assess the impact of testing and interventions for students returning to colleges, or their Halls of Residence from their permanent home addresses. Our analysis was considered by the Welsh Government’s Technical Advisory Group (TAG), Further Education and Higher Education Task Group dealing with Covid-19. Further, the work was also presented to the Environmental Science policy committee, for use in advising how to open up more general social spaces, such as places of worship. Our work has also been communicated to colleagues in the English Government, Scottish Government and Northern Ireland Executive and is currently being used by Bethan Cradock, (Head of Policy HE Covid-19) and Marian Jebb (head of post-16 quality and data management for the Welsh Government) to develop policy for safely returning students back to their places of study.
4.2 Future work
Due to the continued existence of the pandemic there is still plenty be done. Much of the work could focus on making the simulation more accurate. Namely, rather than fixing parameters we could use a Bayesian approach to sample from realistic parameter distributions, which can be generated from data [44, 45, 46, 47]. Equally, current research is focused on generating estimates of real time simulations of airborne particle spread. This could be encompassed into our simulation, but we would need to increase the time resolution from days to hours.
The quickest gain for making the simulation more realistic, particularly in the HE case, would be to nest the algorithm within itself. Nesting the algorithm within itself would give us access to multiple spatial compartments. Namely, one level of the algorithm could be running a Halls of Residence on the scale of grouping everyone into flats, then a second level of the algorithm could be running on the scale of individuals within flats. This would allow the removal of the current restriction of tracking infections up until the point of group isolation.
The development of a nested algorithm would also allow us to simulate infection propagation over multiple classes within the same school. As a result, we would be able to elucidate the impact of the teachers moving from class to class, i.e. the existence of “super spreaders” from internal and external class interactions. Namely, in a next iteration we could track not only when someone is infected, but who infected them. We could then extract the number of secondary infections linked to each infected person and observe whether there are specific individuals that infect others at a rate significantly larger than others. From this point, we could reverse engineer the situations in which the super spreaders find themselves, to see if there are any commonalities which could be perturbed leading to a reduction of their highly infectious nature. Furthermore, the construction a transmission network between all agents would allow for further analysis on the existence of a “super spreader” within the population by determining connectivity bottlenecks from its spectral properties [48].
4.3 Summary
We asked whether it was suitable for Lateral Flow Devices (LFD) to be used as a means of getting students back to school, or university. Our simulated results show repeated testing does help reduce the average number of total infections, as asymptomatic individuals can be found and isolated, resulting in the reduction of infectious individuals. However, we have also found that it is not worth investing in better tests that reduce the false positive probability of the LFD, which has been its major criticism. Instead, time, effort and money are better spent investing in personal protective equipment (e.g. masks) and increasing the quality of ventilation in enclosed environments.
Data Availability
No clinical data was produced in this study. We provide an open-access repository for the code and test files required to run the model outlined in the present study.
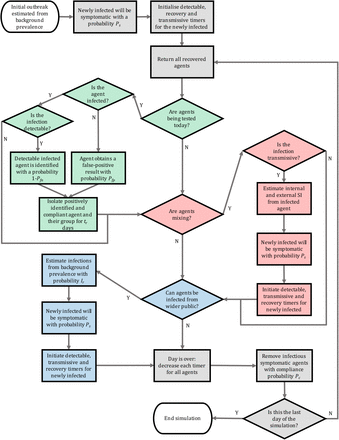
A Individual based model interpretation and implementation
As we developed our computational framework to be used independent of technical background, we supply a list of example real-world infection events and how these events are interpreted within our model (see Table 2). We intend for the model to be analysed, adapted and extended to suit the local requirements, thus Table 2 should allow a user to prescribe the inputs required in their particular case.
Figure 6 provides a flowchart depicting the full algorithm for infection propagation throughout a discrete population, colour-coded in agreement with Figure 1 to highlight optional sub-routines of the algorithm. In addition we provide Table 3, which presents a summary of parameter values used in each scenario in Section 3. Finally, Table 4 provides the reader with definitions of every input parameter to the model.
5 Acknowledgements
JWM is supported by Knowledge Economy Skills Scholarships (KESS2), a pan-Wales higher-level skills initiative led by Bangor University on behalf of the Higher Education sector in Wales. It is part-funded by the Welsh Government’s European Social Fund (ESF).
Footnotes
↵1 Simulations were run on a 2.6 GHz 6-Core Intel Core i7 with 16 GB 2667 MHz DDR4 2019 MacBook Pro.