Abstract
A novel SARS-CoV-2 variant, VOC 202012/01, emerged in southeast England in November 2020 and is rapidly spreading towards fixation. Using a variety of statistical and dynamic modelling approaches, we assessed the relative transmissibility of this novel variant. Depending on the analysis, we estimate that VOC 202012/01 is 43–82% (range of 95% credible intervals 38–106%) more transmissible than preexisting variants of SARS-CoV-2. We did not find clear evidence that VOC 202012/01 results in greater or lesser severity of disease than preexisting variants. Nevertheless, the increase in transmissibility is likely to lead to a large increase in incidence. To assess the potential impact of VOC 202012/01, we fitted a two-strain mathematical model of SARS-CoV-2 transmission to observed COVID-19 hospital admissions, hospital and ICU bed occupancy, and deaths; SARS-CoV-2 PCR prevalence and seroprevalence; and the relative frequency of VOC 202012/01. We find that without stringent control measures, COVID-19 hospitalisations and deaths are projected to reach higher levels in 2021 than were observed in 2020. Control measures of a similar stringency to the national lockdown implemented in England in November 2020 are unlikely to reduce the effective reproduction number Rt to less than 1, unless primary schools, secondary schools, and universities are also closed. We project that large resurgences of the virus are likely to occur following easing of control measures. It may be necessary to greatly accelerate vaccine roll-out to have an appreciable impact in suppressing the resulting disease burden.
In December 2020, evidence began to emerge that a novel SARS-CoV-2 variant, Variant of Concern 202012/01 (henceforth VOC 202012/01), was prevalent and rapidly outcompeting preexisting variants in southeast England (1). The variant increased in incidence during a national lockdown from 5 November – 2 December 2020, which was mandated in response to a previous and unrelated surge in COVID-19 cases, and continued to spread following the lockdown despite many of the most affected areas being under the then-highest level of government-mandated restrictions. Concern over this variant led the UK government to place parts of these three regions under stronger restrictions starting on 20 December 2020, and eventually to impose a third national lockdown on 5 January 2021. As of 19 January 2021, VOC 202012/01 comprises roughly 75% of new SARS-CoV-2 infections in England, and has now been identified in at least 40 countries (2). Our current understanding of effective pharmaceutical and non-pharmaceutical control of SARS-CoV-2 does not reflect potential epidemiological and clinical characteristics of VOC 202012/01. Early estimates of the transmissibility and disease severity for this novel variant are crucial for informing rapid policy responses to this potential threat.
Details of emergent variants
VOC 202012/01 is defined by 17 mutations (14 non-synonymous mutations and 3 deletions), among which eight are located in the spike protein, which mediates SARS-CoV-2 attachment and entry into human cells. At least three mutations have a potential biological significance. Mutation N501Y is one of the key contact residues in the receptor binding domain and has been shown to enhance binding affinity to human angiotensin converting enzyme 2 (ACE2) (3, 4). Mutation P681H is located immediately adjacent to the furin cleavage site in spike, a known region of importance for infection and transmission (5, 6). The deletion of two amino acids at positions 69-70 in spike has arisen in multiple independent circulating lineages of SARS-CoV-2, is linked to immune escape in immunocompromised patients and enhances viral infectivity in vitro (7, 8). This deletion is also responsible for certain commercial testing kits—namely, the Thermo Fisher TaqPath COVID-19 assay—failing to detect the spike glycoprotein gene, with genomic data confirming these S gene target failures (SGTF) are primarily due to the new variant (1). Accordingly, molecular evidence is consistent with a potentially altered infectiousness phenotype for this variant.
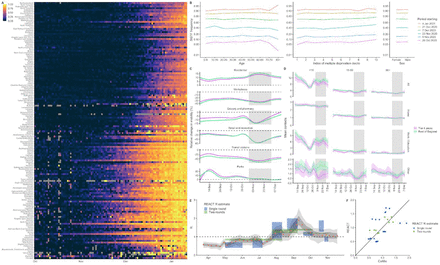
The proportion of COVID-19 cases caused by VOC 202012/01 is increasing rapidly in all regions of England, following an initial expansion in the South East (Fig. 1A), and is spreading at comparable rates among males and females and across age and socioeconomic strata (Fig. 1B). Social contacts and mobility data suggest that the rise in relative prevalence of VOC 202012/01 within England is unlikely to be caused by founder effects: that is, if certain regions had higher levels of transmission as a result of more social interactions, genetic variants that were more prevalent within these regions could become more common overall. However, we did not find evidence of differences in social interactions between regions of high and low VOC 202012/01 prevalence, as measured by Google mobility (9) and social contact survey data from September to December 2020 (10) (Fig. 1B, C), despite that changes in contact patterns closely correlate with changes in the reproduction number inferred from community infection prevalence (Fig 1D, E) and that regionally-differentiated mobility data have previously informed accurate predictions for COVID-19 dynamics in England (11). This apparent decoupling between contact rates and transmission during November and December 2020 could therefore indicate adaptive evolution of the virus.
(A) Proportion of S-gene target failure (SGTF) among positive Pillar 2 community SARS-CoV-2 tests in upper-tier local authorities of England from 1 October 2020–10 January 2021, sorted by latitude.. (B) Spread of SGTF by age, index of multiple deprivation decile (1 = most deprived), and sex within London. (C) Percentage change (95% CI) in Google Mobility indices relative to baseline over time and (D) setting-specific mean contacts (95% CI) from the CoMix study (10) over time and by age for Tier 4 local authorities compared to the rest of England. Tier 4 local authorities are areas within the South East, East of England, and London regions that were placed under stringent restrictions from 20 December 2020 due to high prevalence of VOC 202012/01 and growing case rates. Grey shaded areas show the second national lockdown in England. (E) Estimates of R0 (50% and 95% CI) from CoMix social contact survey (10) compared to Rt estimates from REACT-1 SARS-CoV-2 prevalence survey (15) for England. Rt estimates based on single and aggregated REACT-1 survey rounds are shown.
Assessing the growth of VOC 202012/01
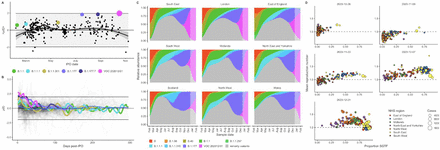
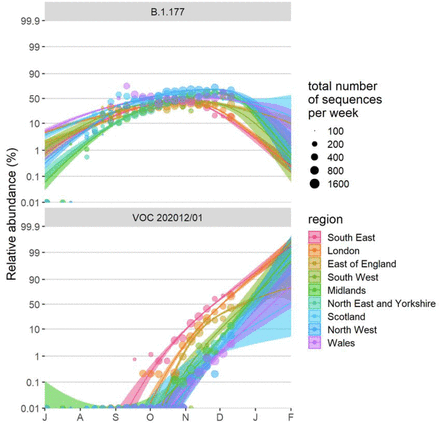
VOC 202012/01 has grown faster than any other defined SARS-CoV-2 lineage in the United Kingdom to date. Analysing all lineages in the COG-UK dataset—which currently comprises over 150,000 sequenced SARS-CoV-2 samples from across the United Kingdom (12)—we found that the relative growth rate of VOC 202012/01 over the first 31 days following its initial phylogenetic observation (IPO) was higher than all 307 other lineages with enough observations to obtain reliable growth rate estimates (Fig. 2A), controlling for changing distributions of growth rates across lineages over time. Moreover, while the relative growth of VOC 202012/01 has changed over time, it remains among the highest as a function of the lineage age, measured in days since IPO (Fig. 2B).
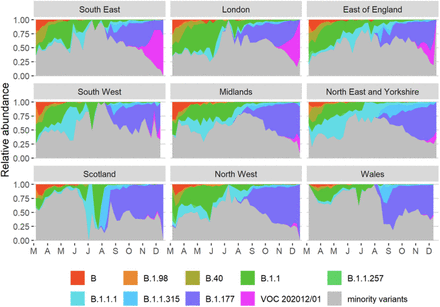
(A) Average relativized fitness in the 31 days following initial phylogenetic observation (IPO) for all lineages in the COG-UKdataset, highlighting many lineages that have risen to prominence including B.1.177, the lineage with the highest relative abundance during the IPO of VOC 202012/01. The shaded regions show conservative 95% rejection intervals and VOC is the first strain to exceed this threshold of faster relativized growth. While many lineages exhibit above-average rates of growth post-IPO, VOC 202012/01 has had the highest average relativized growth of any lineage in the history of COG-UK surveillance of SARS-COV-2. (B) Plotting all lineages’ relativized growth rates as a function of days since IPO with conservative 95% rejection intervals highlights the significantly faster growth of VOC 202012/01 relative to other lineages at comparable times since their IPO. Later declines in VOC and B.1.177 correspond to highly uncertain estimates of growth rates for data that are yet to be backfilled, and so these declines in ρ(t) are sensitive to the processing of future sequences from recent dates (Fig. S1). (C) Muller plots of the relative abundances of the major SARS-CoV-2 variants in the UK, based on a multinomial spline fit to COG-UK sequence data (separate-slopes multinomial spline model, Table 1). A model extrapolation until the end of January is shown (shaded area). Minority variants are 440 circulating SARS-CoV-2 strains that never reached >15% in any week overall. (D) Mean reproduction number over 7-day periods in 149 upper-tier local authorities of England (coloured by the NHS region they are within) plotted against the weekly proportion of Pillar 2 community SARS-CoV-2 tests with SGTF shows the spread of VOC 202012/01, a corresponding increase in the reproduction number by local authority, and the eventual impact of government restrictions. Testing data are shown for the week following the reproduction number estimates to account for delays from infection to test.
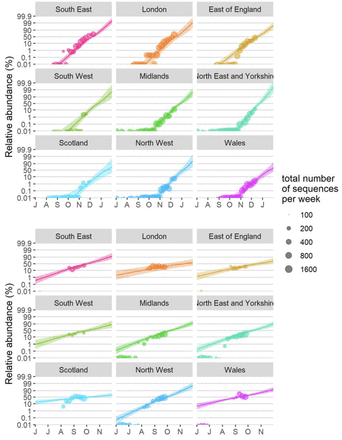
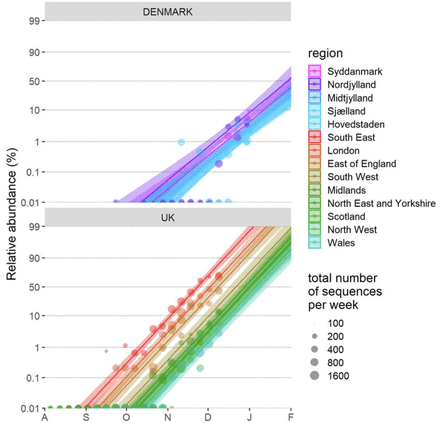
To measure the growth rate of VOC 202012/01, we performed a series of multinomial and logistic regression analyses on the COG-UK data. A time-varying multinomial spline model estimates an increased growth rate for VOC 202012/01 of +0.10 days-1 (95% CI 0.10–0.11) relative to the previously dominant lineage B.1.177 (Fig. 2C); assuming a generation interval of 5.5 days (13), this translates to an increase in the basic reproduction number R by 78% (69–87%). Likewise, a multinomial mixed model, which takes into account spatial heterogeneity across lower-tier local authorities and overdispersion, estimates an increased growth rate of 66% (63-70%) (Fig. S4). Estimating the growth rate of VOC 202012/01 separately across 7 NHS England regions, Scotland, and Wales using a binomial mixed model also identifies few significant differences in the growth rate across regions, and a similar analysis of VOC 202012/01 sequences identified in Denmark yields a compatible estimate of a 59% (44–75%) increase in R. As an alternative approach, we performed a regression analysis of previously-estimated reproduction numbers from case data against the frequency of SGTF in English upper-tier local authorities (UTLAs; Fig. 2D) using local control policies and mobility data as covariates, and including a time-varying spline to capture any unmeasured confounders. This yielded an estimated increase in reproduction numbers associated with VOC 202012/01 of 43% (38-48)%, increasing to a 57% (52-62)% increase if the spline was not included. The various statistical models we fitted yield slightly different estimates for the growth rate of VOC 202012/01, reflecting different assumptions and model structures, but all identify a substantially increased growth rate (Tables 1, S1).
Hypotheses for increased growth rate of VOC 202012/01
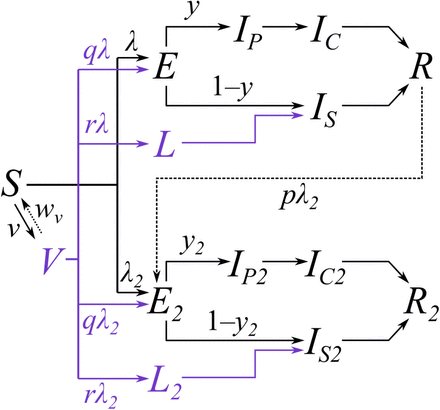
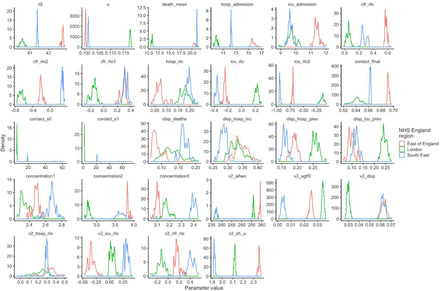
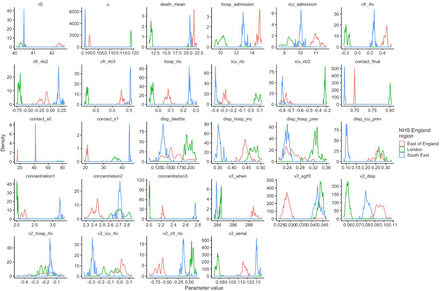
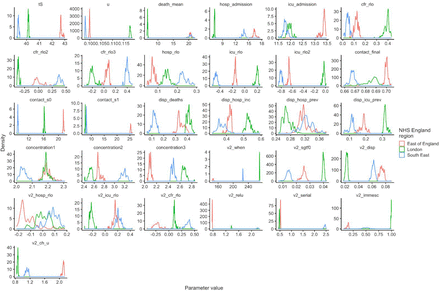
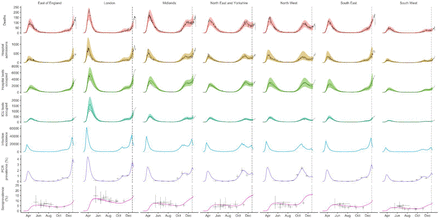
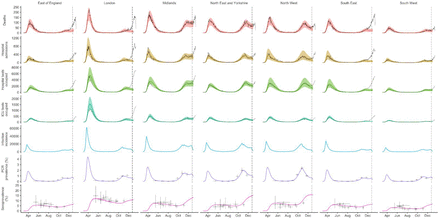
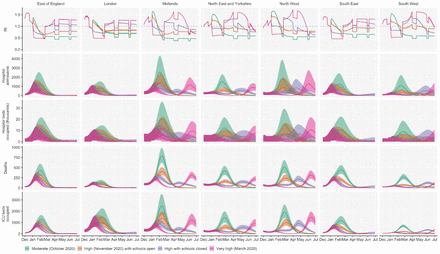
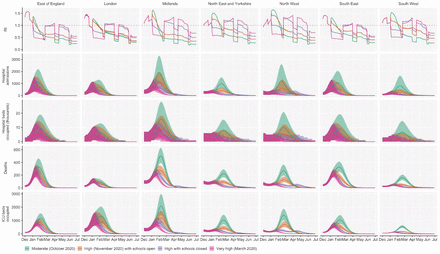
To understand possible biological mechanisms for the observed dynamics of VOC 202012/01, we considered five alternative hypotheses for why the new variant might be spreading more efficiently: increased transmissibility; longer infectious period; immune escape; increased susceptibility among children; and shorter generation time. To assess these hypotheses, we extended an age- and regionally-structured mathematical model of SARS-CoV-2 transmission (14, 16) to consider two co-circulating variants of SARS-CoV-2 (Fig. S9). The model is fitted to observed hospital admissions, hospital and ICU bed occupancy, deaths within 28 days of a positive SARS-CoV-2 test, PCR prevalence, seroprevalence, and the relative frequency of SGTF in Pillar 2 SARS-CoV-2 testing data, across the three most heavily affected NHS England regions: the South East, London, and East of England (Fig. 3). Each model includes a single alternative parameter capturing the hypothesized mechanism (Figs. S10–S15). We fit the models using data up to 24 December 2020 and assessed the performance of each model by comparing Deviance Information Criteria (DIC) and by comparing fitted model projections to observed data from the subsequent 14-day period (25 December 2020 – 7 January 2021).
Each row shows a different assumed mechanism. (A) Relative frequency of VOC 202012/01 (black line and ribbon shows observed SGTF frequency with 95% binomial credible interval; purple line and ribbon shows mean and 95% credible interval for SGTF frequency from model fit). (B) Posterior estimates for relative odds of hospitalisation (severe illness), relative odds of ICU admission (critical illness), relative odds of death (fatal illness), and the parameter that defines the hypothesised mechanism; all parameters are relative to those estimated for preexisting variants. Illustrative model fits for the South East NHS England region: (C) fitted single-strain model without emergence of VOC 202012/01; (D) fitted two-strain increased transmissibility model with VOC 202012/01 removed; (E) fitted two-strain increased transmissibility model with VOC 202012/01 included.
First, we modelled increased infectiousness as an increase in the risk of transmission of VOC 202012/01 per contact, relative to preexisting variants. This model exhibited the best predictive performance of the five hypotheses tested (relative predictive deviance ΔPD = 0) and the second-best fit to the data among the hypotheses tested (DIC = 16627, ΔDIC = 134). Such a mechanism is consistent, in principle, with (disputed (17)) observations of lower Ct values (i.e., higher viral load) for VOC 202012/01 (18).
Second, we modelled a longer infectious period as a multiplicative factor for VOC 202012/01 on the 5-day infectious period assumed for preexisting variants. This model had the second-best predictive performance (ΔPD = 1117) and the third-best fit to the data (DIC = 16641, ΔDIC = 148) of the hypotheses tested. This model would require that the infectious period is approximately doubled in individuals infected with VOC 202012/01; it is not currently known whether individuals infected with VOC 202012/01 have an extended infectious period.
Third, we modelled immune escape by assuming individuals previously infected with preexisting variants had a degree of susceptibility to reinfection by VOC 202012/01. Such a mechanism is consistent with the ΔH69/ΔV70 deletion in spike contributing to immune escape in an immunocompromised patient (7) and could have implications for vaccine effectiveness. However, this model had the second-worst predictive performance (ΔPD = 2,475) and the worst fit to data (DIC = 20456, ΔDIC = 3,963) of the hypotheses tested, and underestimated the observed relative growth rate of VOC 202012/01 even when assuming complete immune escape.
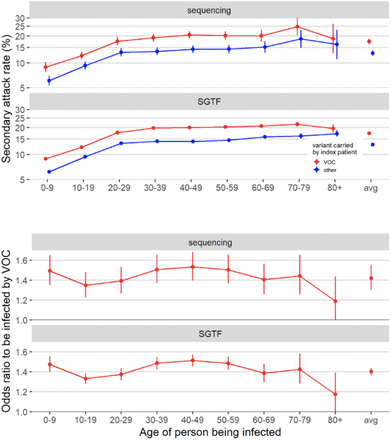
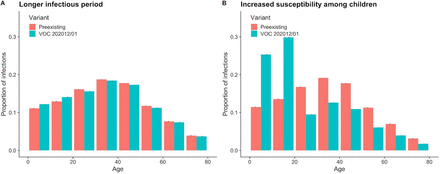
Fourth, we modelled increased susceptibility among children (aged 0-19) by assuming their susceptibility to infection by VOC 202012/01 given exposure was inflated by a multiplicative factor relative to preexisting variants. Evidence suggests children are typically less susceptible to SARS-CoV-2 infection than adults (19, 20), possibly due to immune cross-protection resulting from infection by other human coronaviruses (21). Our baseline model assumes that 0–19-year-olds are approximately half as susceptible to SARS-CoV-2 infection as 20+-year-olds (19); if this were to change for the new variant, it could have implications for the effectiveness of school closures as a control measure. This model had the third-best predictive performance (ΔPD = 1,458) and the best fit to data (DIC = 16493, ΔDIC = 0). However, this model requires that children are roughly twice as susceptible to infection with VOC 202012/01 as they are to preexisting variants. Analysis of household secondary attack rates for VOC 202012/01 identifies a slight increase in secondary attack rate (SAR) among children aged 0-9, but this increase is not statistically significant (binomial GLM, Sidak age group × variant interaction contrast, P = 0.72), and a nonsignificant decrease in SAR among 10-19 year olds (P = 0.32; Fig. S8).
Finally, we modelled a shorter generation time by assuming individuals infected with VOC 202012/01 had a shorter latent period and a shorter infectious period, with the same overall infectiousness. A shorter generation time results in a higher growth rate when Rt> 1, and would have implications for the effectiveness of control measures against this variant, because holding the growth rate of an epidemic constant, a shorter generation time implies a lower reproduction number and hence Rt < 1 is easier to achieve. This final model exhibited the worst predictive performance (ΔPD = 50,927) and the second-worst fit to data (DIC = 17390, ΔDIC = 897), predicting that VOC 202012/01 should have decreased in relative frequency during the stronger restrictions imposed in the south-east of England in late December 2020. When Rt < 1 for both variants, a shorter generation time is a selective disadvantage, because infections will then decline faster compared to a variant with the same Rt but transmitting over a longer timescale.
The five models evaluated here to explain infection resurgence generate further testable hypotheses. For example, an increase in susceptibility among children would, all else being equal, generate a marked increase in cases in children, and reductions across young and middle-aged adults (Fig. S16). Limited cross-protection between variants would entail a higher reinfection rate, while a shorter generation time could be corroborated with epidemiologic investigation. Additional data, when available, could therefore help verify our early findings as well as detect the possibility of combinations of multiple mechanisms. We fitted a combined model incorporating the five hypotheses above, but it was not able to identify a single consistent mechanism across NHS regions (Fig. S15). Based on our analysis, we identify increased transmissibility as the most parsimonious model, but emphasize that the five mechanisms explored here are not mutually exclusive and may be operating in concert.
The fitted model based upon increased transmissibility, which reproduces observed epidemiological dynamics and increases in relative prevalence of VOC 202012/01 (Figs. 3, S17), finds no clear evidence of a difference in odds of hospitalisation (estimated odds ratio of hospitalisation given infection, 1.14 [95% credible intervals 0.76–1.73]), critical illness (OR 1.15 [0.62–2.14]), or relative risk of death (OR 1.09 [0.87–1.36]) associated with VOC 202012/01 based upon fitting to the three most heavily affected NHS England regions. However, the central estimates for all parameters are consistent with increased severity, and we would not expect to identify a clear signal of the severity of disease caused by VOC 202012/01 when fitting to data up to 24 December 2020. In particular, given the substantial lag between infection and death, any increased fatality rate associated with VOC 202012/01 is unlikely to be detectable in this analysis. However, the fitted model finds strong evidence of higher relative transmissibility (Fig. 3B, Table 1), estimated at 60% (95% CrI: 36–87%) higher than preexisting variants for the three most heavily affected NHS England regions, or 71% (39–106%) when estimated across all seven NHS England regions. These estimates are consistent with our statistical estimates (Table 1) and with a previous estimate of 70% increased transmissibility for VOC 202012/01 (18). By contrast, a model without these differences in transmissibility between VOC 202012/01 and preexisting variants was unable to reproduce observed patterns in the data, particularly for December 2020 (Fig. 3C–E, Fig. S17–S19). This further highlights that changing contact patterns cannot explain the spread of VOC 202012/01.
Projections of future dynamics
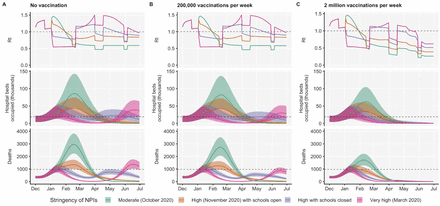
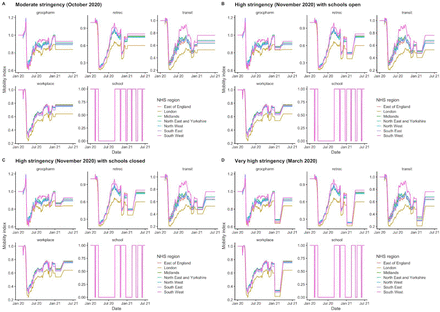
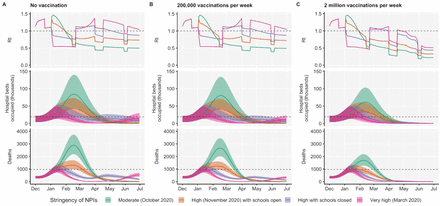
Using the best-performing transmission model (increased transmissibility) fitted to all seven NHS England regions, we compared projected epidemic dynamics under different assumptions about control measures from mid-December 2020 to the end of June 2021. We compared four main scenarios for non-pharmaceutical interventions (NPIs) introduced on 1 January 2021: (i) a moderate-stringency scenario with mobility levels returning to those observed in the first half of October 2020; (ii) a high-stringency scenario with mobility levels decreasing to those observed during the second national lockdown in England in November 2020, with schools open; (iii) the same high-stringency scenario, but with schools closed until 22 February 2021; and (iv) a very high-stringency scenario with mobility levels returning to those observed during the first national lockdown in early April 2020, with schools closed (Fig. S20). In combination with these NPI scenarios, we examined three vaccination scenarios: no vaccinations; 200,000 vaccinations per week; and 2,000,000 vaccinations per week. We assumed that vaccine rollout started on 1 January 2021 and that the vaccine exhibited 95% efficacy against disease and 60% efficacy against infection. For simplicity of modelling, we assumed that vaccine protection was conferred immediately upon receipt of one vaccine dose. These projections serve as indicative scenarios rather than formal predictive forecasts.
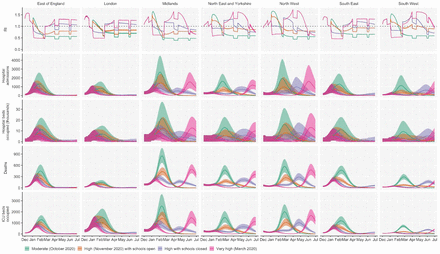
We found that regardless of control measures simulated, all NHS regions are projected to experience a new wave of COVID-19 cases and deaths in early 2021, peaking in February 2021 if no substantial control measures are introduced, or in mid-January 2021 if strong control measures succeed in reducing R to less than 1 (Fig. 4A). In the absence of substantial vaccine roll-out, cases, hospitalisations, ICU admissions and deaths in 2021 may exceed those in 2020, even with stringent NPIs in place (Table 2). Implementing more stringent measures in January 2021 (scenarios iii and iv) leads to a larger rebound in cases when simulated restrictions are lifted in March 2021, particularly in those regions that have been least affected so far (Fig. S21). However, these more stringent measures may buy time to reach more widespread population immunity through vaccination. Vaccine roll-out will further mitigate transmission, although the impact of vaccinating 200,000 people per week—similar in magnitude to the rates reached in December 2020—may be relatively small (Fig. 4B, Fig. S22). An accelerated uptake of 2 million people vaccinated per week is predicted to have a much more substantial impact (Fig. 4C, Fig. S23). The most stringent NPI scenario, along with 2 million individuals vaccinated per week, is the only scenario we considered which reduces peak ICU burden below the levels seen during the first wave (Table 2). However, accelerated vaccine roll-out has a relatively limited impact on peak burden, as the peak is largely mediated by the stringency of NPIs enacted in January 2021, before vaccination has much of an impact. The primary benefit of accelerated vaccine roll-out lies in helping to avert a resurgence of cases following the relaxation of non-pharmaceutical control measures, and in blunting transmission after the peak burden has already been reached.
We compare four alternative scenarios for non-pharmaceutical interventions from 1 January 2021: (i) mobility returning to levels observed during relatively moderate restrictions in early October 2020; (ii) mobility as observed during the second lockdown in England in November 2020, then gradually returning to October 2020 levels from 1 March to 1 April 2021, with schools open; (iii) as (ii), but with school closed until 22 February 2021; (iv) as (iii), but with a lockdown of greater stringency as observed in March 2020 (Fig. S20). (A) Without vaccination. (B) With 200,000 people vaccinated per week. (C) With 2 million people vaccinated per week. We assume that vaccination confers 95% vaccine efficacy against disease and 60% vaccine efficacy against infection, and that vaccination starts on 1 January 2021 with vaccine protection starting immediately upon receipt. This is intended to approximate the fact that vaccination started in early December, but that full protection occurs after a time lag and potentially after a second dose. Vaccines are given first to 70+ year olds until 85% coverage is reached in this age group, then to 60+ year olds until 85% coverage is reached in this age group, continuing into younger age groups in 10-year decrements. Median and 95% credible intervals are shown. The dotted lines in rows 2 and 3 show peak hospitalisations and deaths from the first COVID-19 wave in England (April 2020).
As a sensitivity analysis, we also ran model projections with a seasonal component such that transmission is 20% higher in the winter than in the summer (Kissler et al. 2020), which did not qualitatively affect our results (Fig. S24).
Discussion
Combining multiple behavioural and epidemiological data sources with statistical and dynamic modelling, we estimated that the novel SARS-CoV-2 variant VOC 202012/01 is 43–82% (range of 95% credible intervals 38–106%) more transmissible than preexisting variants of SARS-CoV-2 in England. Existing control measures are likely to be less effective in the face of this new variant, and countries may require stronger proactive interventions to achieve the same level of control. Based on early population-level data, we were unable to identify a clear signal as to whether the new variant is associated with higher disease severity. Theoretical considerations suggest that mutations conferring increased transmissibility to pathogens—such as that exhibited by VOC 202012/01—may be inextricably linked to reduced severity of disease (22). However, a fundamental virulence/transmissibility tradeoff requires that a long history of adaptive evolution has rendered mutations yielding increased transmissibility inaccessible without a decrease in virulence, which does not obviously hold for a recently emerged human pathogen such as SARS-CoV-2. Regardless, without strengthened controls, there is a clear risk that future epidemic waves may be larger – and hence associated with greater burden – than previous waves. The UK government initiated a third national lockdown on 5 January 2021 in response to the rapid spread of VOC 202012/01, including school closures. Educational settings are among the largest institutions linked to SARS-CoV-2 clusters that remained open during November and December 2020 (23), which means the enacted school and university closures may substantially assist in reducing the burden of COVID-19 in early 2021.
The rise in transmission from VOC 202012/01 has crucial implications for vaccination. First, it means prompt and efficient vaccine delivery and distribution is even more important to reduce the impact of the epidemic in the near future. Additionally, increased transmission resulting from VOC 202012/01 will raise the herd immunity threshold, meaning the potential future burden of SARS-CoV-2 is larger and higher vaccination coverage will be required to achieve herd immunity. It is extremely concerning that VOC 202012/01 has already been identified in at least 40 countries globally (2). Given the relatively high rate of travel between the UK and other countries, and the high sequencing capacity in the UK relative to other locations worldwide (24), the new variant is likely to have spread even more extensively without yet having been detected. Moreover, although VOC 202012/01 was first identified in England, a rapidly spreading variant with similar phenotypic properties has also been detected in South Africa (25), where there has been a marked increase in transmission in late 2020, and another variant exhibiting immune escape has emerged in Brazil (26). Thus, vaccination timelines will also be a crucial determinant of future burden in other countries where similar new variants are present. Second, there is a need to determine whether VOC 202012/01 – or any subsequent emerging lineages – could affect the efficacy of vaccines. Vaccine developers may therefore need to consider experimenting with variant sequences as a precautionary measure, and powering post-licensure studies to detect differences in efficacy between the preexisting and new variants. Licensing authorities may need to clarify abbreviated pathways to marketing for vaccines that involve altering strain formulation without any other changes to their composition.
We have examined the impact of a small number of intervention and vaccination scenarios, and the scenarios we project should not be regarded as the only available options for policymakers. Moreover, there are substantial uncertainties not fully captured by our model: for example, we do not explicitly model care home or hospital transmission of SARS-CoV-2, and we assume that there are no further changes in the infection fatality ratio (IFR) of SARS-CoV-2 in the future. The IFR for SARS-CoV-2 declined substantially in the UK over mid-2020 (11) and it may decrease again in 2021, or increase if there are substantial pressures on the health service. Finally, there are uncertainties in the choice of model used to generate these predictions, and the exact choice will yield differences in the measures needed to control the epidemic. We note that even without increased susceptibility of children to VOC 202012/01, the more efficient spread of the variant implies that the difficult societal decision of closing schools will be a key public health question for multiple countries in the months ahead.
There are some limitations to our analysis. We can only assess relative support in the data for the hypotheses proposed, but there may be other plausible mechanisms driving the resurgence of cases that we did not consider. Our conclusions about school closures were based on the assumption that children had reduced susceptibility and infectiousness compared to adults (19), whereas the precise values of these parameters and the impact of school closures (27) remains the subject of scientific debate (27). We based our assumptions about the efficacy of control measures on the measured impact on mobility of previous national lockdowns in England, but cannot predict the impact of policy options with certainty. Finally, as the emergence of VOC 202012/01 has only recently been identified, our estimates may change substantially as more data become available.
Despite these limitations, we found strong evidence that VOC 202012/01 is spreading significantly faster than preexisting SARS-CoV-2variants. Our modelling analysis suggests this difference can be explained by an overall higher infectiousness of VOC 202012/01 but not by a shorter generation time or immune escape alone. Further experimental work could provide insights into the biological mechanisms for our observations, but given our projections of a rapid rise in future incidence from VOC 202012/01 without additional control measures—and the detection of other novel and highly-transmissible variants in South Africa (25) and Brazil (26)—there is an urgent need to consider what new approaches may be required to sufficiently reduce the ongoing transmission of SARS-CoV-2.
Data Availability
All analysis code and data have been made publicly available.
Competing interests
ADW owns Selva Analytics LLC. All other authors declare no competing interests.
Author contributions and acknowledgements
Nicholas G. Davies, Sam Abbott, Rosanna C. Barnard, Christopher I. Jarvis, Adam J. Kucharski, James Munday, Carl A. B. Pearson, Timothy W. Russell, Damien C. Tully, Alex D. Washburne, Tom Wenseleers, Amy Gimma, William Waites, Kerry LM Wong, Kevin van Zandvoort, Justin D. Silverman, Karla Diaz-Ordaz, Ruth Keogh, Rosalind M. Eggo, Sebastian Funk, Mark Jit, Katherine E. Atkins, and W. John Edmunds conceived the study, performed analyses, and wrote the manuscript. The CMMID COVID-19 Working Group provided discussion and comments. Alex Selby suggested improvements to the analysis code. Stefan Flasche, Rein Houben, Stéphane Hué, Yalda Jafari, Mihály Koltai, Fabienne Krauer, Yang Liu, Rachel Lowe, Billy Quilty, and Julián Villabona Arenas gave input during conception and manuscript drafting.
The CMMID COVID-19 Working Group is (randomized order): Sophie R Meakin, James D Munday, Amy Gimma, Rosanna C Barnard, Timothy W Russell, Billy J Quilty, Yang Liu, Stefan Flasche, Jiayao Lei, Adam J Kucharski, William Waites, Sebastian Funk, Fiona Yueqian Sun, Fabienne Krauer, Rachel Lowe, Nikos I Bosse, Damien C Tully, Emily S Nightingale, Katharine Sherratt, Rosalind M Eggo, Kaja Abbas, Kathleen O’Reilly, Hamish P Gibbs, C Julian Villabona-Arenas, Naomi R Waterlow, W John Edmunds, Graham Medley, Oliver Brady, Jack Williams, Alicia Rosello, Christopher I Jarvis, Petra Klepac, Mihaly Koltai, Nicholas G. Davies, Frank G Sandmann, Anna M Foss, Sam Abbott, Yalda Jafari, Kiesha Prem, Yung-Wai Desmond Chan, Katherine E. Atkins, Carl A B Pearson, Joel Hellewell, Kevin van Zandvoort, Simon R Procter, Thibaut Jombart, Gwenan M Knight, Akira Endo, Matthew Quaife, Mark Jit, Alicia Showering, Samuel Clifford.
Funding declarations for the CMMID COVID-19 Working Group are as follows. SRM: Wellcome Trust (grant: 210758/Z/18/Z). JDM: Wellcome Trust (grant: 210758/Z/18/Z). AG: European Commission (EpiPose 101003688). RCB: European Commission (EpiPose 101003688). TWR: Wellcome Trust (grant: 206250/Z/17/Z). BJQ: This research was partly funded by the National Institute for Health Research (NIHR) (16/137/109 & 16/136/46) using UK aid from the UK Government to support global health research. The views expressed in this publication are those of the author(s) and not necessarily those of the NIHR or the UK Department of Health and Social Care. BJQ is supported in part by a grant from the Bill and Melinda Gates Foundation (OPP1139859). YL: Bill & Melinda Gates Foundation (INV-003174), NIHR (16/137/109), European Commission (101003688). SFlasche: Wellcome Trust (grant: 208812/Z/17/Z). JYL: Bill & Melinda Gates Foundation (INV-003174). AJK: Wellcome Trust (grant: 206250/Z/17/Z), NIHR (NIHR200908). WW: UK Medical Research Council (MRC) (grant MR/V027956/1). SFunk: Wellcome Trust (grant: 210758/Z/18/Z), NIHR (NIHR200908). FYS: NIHR EPIC grant (16/137/109). FK: Innovation Fund of the Joint Federal Committee (Grant number 01VSF18015), Wellcome Trust (UNS110424). RL: Royal Society Dorothy Hodgkin Fellowship. NIB: Health Protection Research Unit (grant code NIHR200908). DCT: No funding declared. ESN: Bill & Melinda Gates Foundation (OPP1183986). KS: Wellcome Trust (grant: 210758/Z/18/Z). RME: HDR UK (grant: MR/S003975/1), MRC (grant: MC_PC 19065), NIHR (grant: NIHR200908). KA: Bill & Melinda Gates Foundation (OPP1157270, INV-016832). KO’R: Bill and Melinda Gates Foundation (OPP1191821). HPG: This research was produced by CSIGN which is part of the EDCTP2 programme supported by the European Union (grant number RIA2020EF-2983-CSIGN). The views and opinions of authors expressed herein do not necessarily state or reflect those of EDCTP. This research is funded by the Department of Health and Social Care using UK Aid funding and is managed by the NIHR. The views expressed in this publication are those of the author(s) and not necessarily those of the Department of Health and Social Care (PR-OD-1017-20001). CJVA: European Research Council Starting Grant (Action number 757688). NRW: Medical Research Council (grant number MR/N013638/1). WJE: European Commission (EpiPose 101003688), NIHR (NIHR200908). GFM: NTD Modelling Consortium by the Bill and Melinda Gates Foundation (OPP1184344). OJB: Wellcome Trust (grant: 206471/Z/17/Z). JW: NIHR Health Protection Research Unit and NIHR HTA. AR: NIHR (grant: PR-OD-1017-20002). CIJ: Global Challenges Research Fund (GCRF) project ‘RECAP’ managed through RCUK and ESRC (ES/P010873/1). PK: This research was partly funded by the Royal Society under award RP\EA\180004, European Commission (101003688), Bill & Melinda Gates Foundation (INV-003174). MK: Foreign, Commonwealth and Development Office / Wellcome Trust. NGD: UKRI Research England; NIHR Health Protection Research Unit in Immunisation (NIHR200929); UK MRC (MC_PC_19065). FGS: NIHR Health Protection Research Unit in Modelling & Health Economics, and in Immunisation. AMF: No funding declared. SA: Wellcome Trust (grant: 210758/Z/18/Z). YJ: LSHTM, DHSC/UKRI COVID-19 Rapid Response Initiative. KP: Bill & Melinda Gates Foundation (INV-003174), European Commission (101003688). YWDC: No funding declared. KEA: European Research Council Starting Grant (Action number 757688). CABP: CABP is supported by the Bill & Melinda Gates Foundation (OPP1184344) and the UK Foreign, Commonwealth and Development Office (FCDO)/Wellcome Trust Epidemic Preparedness Coronavirus research programme (ref. 221303/Z/20/Z). JH: Wellcome Trust (grant: 210758/Z/18/Z). KvZ: KvZ is supported by the UK Foreign, Commonwealth and Development Office (FCDO)/Wellcome Trust Epidemic Preparedness Coronavirus research programme (ref. 221303/Z/20/Z), and Elrha’s Research for Health in Humanitarian Crises (R2HC) Programme, which aims to improve health outcomes by strengthening the evidence base for public health interventions in humanitarian crises. The R2HC programme is funded by the UK Government (FCDO), the Wellcome Trust, and the UK National Institute for Health Research (NIHR). SRP: Bill and Melinda Gates Foundation (INV-016832). TJ: RCUK/ESRC (grant: ES/P010873/1); UK PH RST; NIHR HPRU Modelling & Health Economics (NIHR200908). GMK: UK Medical Research Council (grant: MR/P014658/1). AE: The Nakajima Foundation. MQ: European Research Council Starting Grant (Action Number #757699); Bill and Melinda Gates Foundation (INV-001754). MJ: Bill & Melinda Gates Foundation (INV-003174, INV-016832), NIHR (16/137/109, NIHR200929, NIHR200908), European Commission (EpiPose 101003688). AS: No funding declared. SC: Wellcome Trust (grant: 208812/Z/17/Z).
Methods
Summary of second wave control measures in England
In response to a resurgence of cases in September and October 2020, a second national lockdown was implemented in England, lasting from the 5 November to the 2 December 2020. Restrictions included a stay-at-home order with a number of exemptions including for exercise, essential shopping, obtaining or providing medical care, education and work for those unable to work from home. Schools were kept open. Non-essential shops, retail and leisure venues were required to close. Pubs, bars and restaurants were allowed to offer takeaway services only. Following the end of this second national lockdown, regions in England were assigned to tiered local restrictions according to medium, high and very high alert levels (Tiers 1, 2 and 3). In response to rising cases in southeast England and concerns over VOC 202012/01, the UK government announced on 19 December 2020 that a number of regions in southeast England would be placed into a new, more stringent ‘Tier 4’, corresponding to a Stay at Home alert level. Regional Tier 4 restrictions were broadly similar to the second national lockdown restrictions. As cases continued to rise and VOC 202012/01 spread throughout England, on 5 January 2021 a third national lockdown was introduced in England, with schools and universities closed and individuals advised to stay at home, with measures to be kept in place until at least mid-February 2021.
Data sources
To assess the spread of VOC 202012/01 in the United Kingdom, we used publicly-available sequencing-based data from the COG-UK Consortium (12, 28) and Pillar 2 SARS-CoV-2 testing data provided by Public Health England for estimating the frequency of S-gene target failure (SGTF) in England. COG-UK sequencing data for Northern Ireland were only available up to 20 November 2020 at the time of analysis, which precluded us from including Northern Ireland in our statistical estimates for the growth of VOC 202012/01 in the UK.
To estimate mobility, we used anonymised mobility data collected from smartphone users by Google Community Mobility (9). Percentage change in mobility per day was calculated for each lower-tier local authority in England and a generalised additive model with a spline for time was fitted to these observations to provide a smoothed effect of the change in mobility over time (Fig. 1C).
To estimate social contact rates (Fig. 1D), we used data on reported social contacts from the CoMix survey (10), which is a weekly survey of face-to-face contact patterns, taken from a sample of approximately 2500 individuals broadly representative of the UK population with respect to age and geographical location. We calculated the distribution of contacts using 1000 bootstrap samples with replacement from the raw data. Bootstrap samples were calculated at the participant level, then all observations for those participants are included in a sample to respect the correlation structure of the data. We collect data in two panels which alternate weekly, therefore we calculated the mean smoothed over the 2 week intervals to give a larger number of participants per estimate and account for panel effects. We calculated the mean number of contacts (face to face conversational contact or physical contact) in the settings “home”, “work”, “education” (including childcare, nurseries, schools and universities and colleges), and “other” settings. We calculate the mean contacts by age group and area of residence (those areas which were subsequently placed under Tier 4 restrictions on 20 December 20 as they were experiencing high and rapidly increasing incidence, and those areas of England that were not placed under these restrictions). The mean number of contacts is influenced by a few individuals who report very high numbers of contacts (often in a work context). The means shown here are calculated based on truncating the maximum number of contacts recorded at 200 per individual per day.
Statistical methods in brief
See Supplemental Online Material for full details.
Growth of VOC 202012/01 following initial phylogenetic observation
For each lineage i in the COG-UK dataset, we pool the number of sequences observed within that lineage across the UK for every day, t, yielding integer-valued sequence counts N(i, t). We estimate the time-varying exponential growth rates of cases of each strain, r(i, t), using a negative binomial state-space model correcting for day-of-week effects whose dispersion parameter was optimized for each strain by marginal likelihood maximization. We defined the relativized growth rate of a lineage i at time t as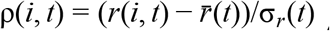 
, where 
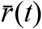is the average growth rate of all circulating strains at time t and σr (t) the standard deviation of growth rates across all lineages at time t, such that ρ(i, t) is analogous to a z-statistic or Wald-type statistic and allows comparison of growth rate differences across time when the average growth rate and scale of growth rate differences varies.
Competitive advantage and increased transmissibility of VOC-202012/01
To estimate the increase in growth rate of VOC 202012/01, we fitted a set of multinomial and binomial generalized linear mixed models (GLMMs), in which we estimated the rate by which the VOC displaces other resident SARS-CoV-2 variants, both across different regions in the UK, as well as in Denmark. All models took into account sample date and region plus, if desired, their interaction, and the mixed models also included local-tier local authority as a random intercept and took into account possible overdispersion. From these models, we estimate the difference in Malthusian growth rate between other competing variants Δr, as well as the expected multiplicative increase in basic reproduction number Rt and infectiousness, assuming unaltered generation time, which can be shown to be equal to exp(Δr .T), where T is the mean generation interval. In our calculations, we used estimated SARS-CoV2 mean generation times T of either 5.5 days(13) (Table 1) or 3.6 days(29, 30) (Table S1).
Rt analysis
We calculated the weekly proportion of positive tests that were S-gene negative out of all positive tests that tested for the S-gene by English upper-tier local authority. We used reproduction number estimates obtained using the method described in (29) and (31) and implemented in the EpiNow2 R package (32), downloaded from https://github.com/epiforecasts/covid-rt-estimates/blob/master/subnational/united-kingdom-local/cases/summary/rt.csv. We then built a separate model of the expected reproduction number in UTLA i during week t starting in the week beginning the 5 October 2020 as a function of local restrictions, mobility indicators, residual temporal variation, and proportion of positive tests S-gene negative. The residual temporal variation is modelled either as a region-specific thin-plate regression spline (“Regional time-varying”) or a static regional parameter (“Regional static”). The key estimand is the relative change in reproduction number in the presence of the SGTF that is not explained by any of the other variables.
Transmission dynamic model
We extended a previously developed modelling framework structured by age (in 5-year age bands, with no births, deaths, or aging due to the short timescales modelled) and by geographical region (11, 14) to include two variants of SARS-CoV-2 (VOC 202012/01 and non-VOC 202012/01) (Fig. S9). The model is a discrete-time deterministic compartmental model which allows for arbitrary delay distributions for transitions between compartments. We fitted this model to multiple regionally-stratified data sources across the 7 NHS England regions as previously: deaths, hospital admissions, hospital bed occupancy, ICU bed occupancy, daily incidence of new infections, PCR prevalence of active infection, seroprevalence, and the daily frequency of VOC 202012/01 across each of the regions as measured by SGTF frequency corrected for false positives. To model school closure, we removed all school contacts from our contact matrix based upon POLYMOD data and varying over time according to Google Mobility indices, as described previously (11)(11). See Supporting Information for details of Bayesian inference including likelihood functions and prior distributions.
Our individual transmission model fits to separate NHS regions of England produce independent estimates of parameters such as relative transmissibility and differences in odds of hospitalisation or death resulting from infection with VOC 202012/01. In order to produce overall estimates for these parameters, we model posterior distributions from individual NHS regions as draws from a mixture distribution, comprising a normally-distributed top-level distribution from which central estimates for each NHS region are drawn. We report the mean and credible intervals of the top-level distribution when reporting model posterior estimates for England.
In model fitting, we assume that our deterministic transmission model approximates the expectation over stochastic epidemic dynamics. This is not exact (Royal Statistical Society Publications), but the error in this approximation is small for the population-level processes we are modelling, as it decays with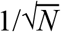 
(Ethier and Kurtz 1986). This approach is well developed for state space models of communicable disease dynamics that fit an epidemic process to observed data via a stochastic observation process.
Apparent growth of VOC 202012/01 not a result of testing artefacts
The apparent frequency of VOC 202012/01 could be inflated relative to reality if this variant leads to increased test-seeking behaviour (e.g. if it leads to a higher rate of symptoms than preexisting variants). However, this would not explain the growth in the relative frequency of VOC 202012/01 over time. Mathematically, if variant 1 has growth rate r1 and variant 2 has growth rate r2, the relative frequency over time is exp(r2t) / (exp(r1t) + exp(r2t)). However, if variant 1 has probability x of being reported and variant 2 has probability y, and both have growth rate r, the relative frequency over time is y exp(rt) / (x exp(rt) + y exp(rt)), which is constant.
Code and data availability
Analysis code and data are available at https://www.github.com/nicholasdavies/newcovid. Analysis code and data for the Rt analysis are available at https://github.com/epiforecasts/covid19.sgene.utla.rt.
Supporting Information
Growth rate of VOC 202012/01 following its initial phylogenetic observation
It’s possible a strain could get lucky and have faster growth rates than other strains, appearing more transmissible despite not being so. Several confounds can affect the significance of an inference of faster growth in a strain such as VOC 202012/01. For instance, any correlated patterns in people of that network can affect the probability a strain has an impressive run of faster growth rates than other strains - if a new strain discovers a region of a contact network with a higher fraction of susceptible people than that experienced by other strains elsewhere on the contact network, then the lucky strain in a pool of susceptible people may appear to grow faster due to the human population structure and not the virus’ phenotypic traits. Similarly, any changes in NPIs that increase the average risk of transmission across subsets of the contact network (e.g. variation in the tier level across the UK) or any patterns of behavior that increase the variability of the risk of transmission across people in the network (e.g. when some connected groups of people have a higher-than-average risk of transmission due to occupation, less participation in transmission-reducing behaviors, etc.) might affect the probability that a strain exhibits a large run such as that seen in VOC 202012/01.
Furthermore, since defining a “new strain” requires at least 5 genomes of at least 95% coverage co-localized in space (33) it’s possible that newly named strains could be more likely to have faster-than-average growth rates as these growing branches of the viral phylogeny may be bioindicators of a spatially (or contact-network) autocorrelated pool of susceptible people with room for further, faster growth.
In this section, we aim to control for time-varying average growth rates, heterogeneity in population structure, and the potential for lineages to be bioindicators of spatially-autocorrelated susceptible populations with an expectation of faster growth after the initial phylogenetic observation (IPO) of the lineage. When accounting for time-varying average growth rates across lineages in circulation, the time varying scale fitness differences across lineages at every point in time, and the time since the initial phylogenetic observation (IPO), the VOC 202012/01 stands out as having the fastest post-IPO relative growth of any lineage in the COG-UK dataset (Fig. 2A&B, main text).
This analysis centered around what we refer to as the “relativized growth rate”. For each lineage i in the COG metadata dataset, we pool the number of sequences observed within that lineage across the UK for every day, t, yielding integer-valued sequence counts N(i, t). We estimate the time-varying exponential growth rates of cases of each strain, r(i, t), using a negative binomial state-space model whose dispersion parameter was optimized for each strain by marginal likelihood maximization. The negative binomial state-space model was implemented using the R package KFAS (34) to estimate abundances and growth rates with a second-order polynomial trend to capture time-varying exponential growth/decay and a 7-day seasonal component to correct for day-of-week effects.
To remove the impact of leading zeros on estimates of growth rates, we started estimating growth rates on the first date for which the following week contained at least three observations of the lineage (including the first observation of that week) – we call the first date of this week the “initial phylogenetic observation” or IPO of the lineage. For lagging zeroes, we removed any zeroes after 7 days of consecutive zeros which continued until the final date used in this analysis. As a result of this filtering of leading and lagging zeroes, there was a variable number of lineages each day, but these lineages served as a minimal set of lineages whose growth rates can serve as a reference frame for assessing the significance of the growth and changes in relative abundance of the VOC (35).
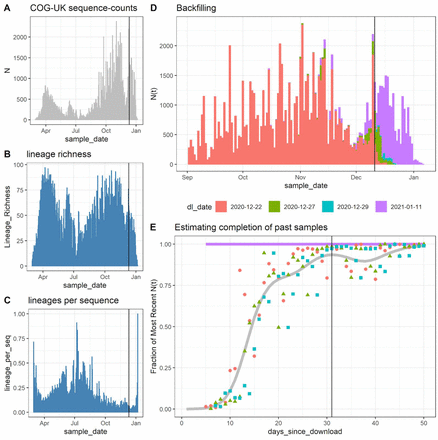
The final date used in this analysis was determined by an analysis of backfilling patterns of the COG-UK dataset. The COG-UK dataset contains a “sample date” column for every sequence, and samples are not added on the date they are collected but back-filled once samples are shipped, sequenced, and uploaded. As a consequence, the recent dates in the COG-UK dataset exhibit a decline in the total number of counts and lineage richness, a period during which there will be biases in comparing growth rates across lineages with different relative abundances as rare lineages flat-line with zero observations and the observed counts of abundant lineages continue to decline. These biases during the period of backfilling can be further confounded by any differences in the processing times of sequences across surrogate data providers which sample different, non-representative subsets of the UK population. By downloading the COG-UK dataset at multiple dates, we find that over 90% of sequences are accounted for 1 month prior to the download date. Therefore, to avoid biases and confounds due to backfilling, we limit our analysis of growth rates to all but the last 1 month of data in the COG-UK dataset. This results in estimation of growth rates of the VOC up to December 12th, 2020 (Fig. S1).
To control for time-varying average growth rates, we defined a statistic we refer to as relativized growth rates, denoted ρ(i, t) for each lineage i and time t,
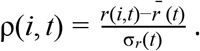
Where 
is the average growth rate of all circulating strains at time t and σr (t) the standard deviation of growth rates across all lineages at time t. This statistic is analogous to a z-statistic or Wald-type statistic and allows comparison of growth rate differences across time when the average growth rate and scale of growth rate differences varies. We compute the average relativized fitness of each lineage for the first month after its IPO. This statistic reflects how much faster the lineage grew compared to other lineages circulating for that same month, and allows us to control for potential IPO-effects of lineages whose first observations came at different times in the UK COVID epidemic.
For a lineage to increase in frequency, it mainly needs to increase faster than the lineage with the highest relative abundance, whereas to have an above-average relativized fitness it will need to increase faster than the average lineage (36). As such, analyzing relativized growth rates is an additional way to assess not just whether VOC 202012/01 grew faster than the dominant lineage B 1.177—as it’s possible other lineages with similar rarity could have had similar runs of positive growth—but rather test whether or not VOC 202012/01 consistently beat out all other lineages, including the rare ones and recent IPOs, and whether this burst of positive growth post-IPO in the VOC exceeds that of other major lineages’ post-IPO relativized growth.
We plot the relativized fitness as a function of days-since-IPO across all lineages, highlighting a few lineages that have risen to high relative abundance over the course of 2020 (Fig. 2A & B, main text).
Competitive advantage and increased transmissibility of the SARS-CoV2 VOC-202012/01
To infer the competitive advantage of the VOC-202012/01 over other circulating SARS-CoV2 strains (Fig. 2C, main text; Figs. S2–S7) we use the COG-UK sequencing data to calculate the rate by which the strain is displacing other variants and increases in relative abundance p. Formally, this is quantified based on the selection (37) rate coefficient s, which for a newly invading variant is defined as (38)
This coefficient measures the rate at which any new variant would displace the resident variant in terms of the increase in the log(odds) to encounter the new variant. A great advantage of the selection rate coefficient is that it can readily be calculated from a logistic regression model as the slope of the proportion of the new variant on a logit (log-odds) link scale. We can further observe that since the ratio of relative frequencies is equal to the ratio of the absolute representation of the new variant V and the wild-type W that (38)
Hence, if selection is density independent and there are no interactions between genotypes, the selection rate is also equal to the difference in Malthusian growth rates between the new variant (rV) and wild-type (rW) (38):
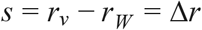
If we further multiply the selection rate by mean generation time T then we obtain the dimensionless selection coefficient (38)
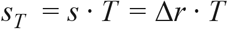
Selection coefficients s and sT represent the most direct measures possible of the fitness advantage enjoyed by any new variant, and are the best possible predictors of whether or not it is expected to increase in frequency during an outbreak (39). However, assuming that the generation time of the competing variants remain unaltered (e.g. that the non-infectious period after exposure remains the same), it is also possible to relate the selection coefficient sTto the expected multiplicative increase in the infectiousness of the virus, as measured by the ratio of the basic reproduction number Rt of the new variant relative to that of the wild type. Specifically, if generation time is gamma distributed with mean T and SD σ, and if we set k = (σ/T)2, it is the case that the basic reproduction number (40) Rt
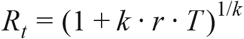
Furthermore, for small k (small SD of the generation time σ relative to the mean T), the following approximation (41) holds
From this, it follows that the ratio of the effective reproduction number of the invading new variant RV relative to that of the wild type RW, i.e. the expected multiplicative increase in the Rt value M, assuming no change in generation time T between the variants, equals approximately
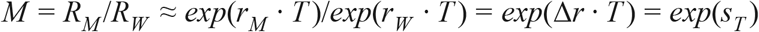
Although this formula is strictly speaking only exact for the limit of k → 0, in practice with our parameter estimates, the error made is extremely small (41) even for larger k. E.g. with rM = Δr = 0.11, rW = 0, T = 5.5 days and σ = 1.8 (13), k = 0.33 and application of the exact formula (5) would yield M = 1.71, whilst the approximate formula (7) would yield M = 1.73, which would amount to an error on M of only 1.6%. The exact formula (5) could only be used if we would be able to estimate the variant-specific intrinsic growth rates rV and rW (38) separately, e.g. using the raw counts, to which one could fit a spline-based Poisson GLM, to yield intrinsic growth rates as the first derivative of the fitted curve on the log link scale. Such a fit, however, would show very large fluctuations due to the implementation of various non-pharmaceutical interventions, and would also require accurate corrections for changes in testing and sequencing intensity over time. Hence, such a calculation would carry a much larger error. Instead, it is much more accurate to estimate the expected multiplicative effect on Rt from the rate of change in the log(odds) of the relative abundance of any new variant p, Δr.
To estimate pairwise differences in growth rates Δr between the VOC variant and other sets of lineages, i.e. pairwise selection rate coefficients, we used both binomial GLMMs (generalized linear mixed models), using data on the representation of pairs of lineages in the COG-UK (12) sequencing data at time of invasion, as well as multinomial spline regression or multinomial mixed models, where we could simultaneously consider the competition for representation among all the major SARS-CoV-2 variants and lineages in different regions across the UK. In both sets of analyses, we considered both the Δr of the VOC 202012/01 (defined as lineage B.1.1.7 and carrying defining mutation N501Y and deletion Δ69/Δ70 in the spike protein) relative to either the earlier dominant lineage B.1.177 (42), a set of 440 minority variants, which never reached >15% in the aggregated UK counts in any week or all other circulating variants. For lineage B.1.177, we included any later descendent lineages into the same group.
Binomial GLMMs fit to the UK data included a fixed factor for NHS England region, a continuous covariate for sampling date, the interaction between both if this yielded a more parsimonious fit (based on the Bayesian Information Criterion) or if we were specifically interested to test for differences in rates of spread across regions, as well as random effects for the local-tier local authority (LTLA) and an observation-level random effect to take into account overdispersion (43). These GLMMs were fit using R’s glmer function in the lme4 package version 1.1.23. For these binomial GLMMs, we used the part of the data where either variant VOC 202012/01 or lineage B.1.177 were initially invading, and for which there was good linearity on a logit scale (Fig. S3). For VOC 202012/01, we therefore used the subset of the data from August 1 2020 onwards, while for lineage B.1.177 we used data for the period between July 1st 2020 and September 30 2020, before it starting to be displaced by VOC 202012/01. From these binomial GLMMs, we subsequently estimated the selection rate Δr from the slope in the log(odds) to encounter the focal variant. Both this slope as well as its 95% confidence intervals were estimated using the emtrends function in the emmeans R package version 1.5.1. Model predictions or marginal mean model predictions and 95% confidence intervals as well as Tukey posthoc tests to test for differences in slopes (rates of displacement of other strains) across regions were also calculated using this same package. In the calculation of marginal means, we used a bias correction for the presence of the random (44) effects. Under the assumption of unaltered generation times, we also made two estimates of the expected multiplicative effect on the Rt value, M1 and M2, based on eqn. (7) above, M = RM /RW≈ exp(Δr · T), using estimated SARS-CoV2 mean generation times T of either 5.5 days (13) or 3.6 days (29, 30). Both the mean and confidence intervals on Δr · T were exponentiated, in this way resulting in the estimated geometric mean multiplicative effect on Rt.
To be able to make another independent baseline estimate of Δr outside the UK, we also used a binomial GLMM to estimate the rate of spread by which VOC 202012/01 is displacing other variants in Denmark, where SARS-CoV2 sequencing is carried out approximately randomly with respect to sample variant identity, and for which data on the incidence of the VOC 202012/01 (lineage B.1.1.7) aggregated by week and by region are openly available (45). These analyses either used the Danish data alone (using data from week 39 of 2020 until week 1 of 2021), or used a combined analysis of the Danish and UK data (also aggregated by region and week, to match the Danish data, and including data from August 1 2020 onwards). These analyses included region as a fixed factor, sample date as a continuous covariate as well as country and country × sample date in the combined DK+UK analysis, plus an observation-level random effect to take into account overdispersion.
Finally, we also fitted two multinomial models in which we considered the multinomial spline model to the COG-UK sequence data using the multinom function of the nnet R package (46) considering the frequencies of 9 major SARS-CoV2 lineages (all reaching at least 15% in some week) as separate variant outcome levels, and subsuming the remaining 440 variants in a category of “minor variants”, thereby allowing us to simultaneously model the competition for representation among all the major variants. This model included a fixed factor region plus a natural cubic spline in function of sample date to allow for slight variation in the selection rate in function of time, plus the interaction between both to allow for different selection rates across regions. A two-degree of freedom natural cubic spline was chosen, as this model both resulted in a visually realistic fit and in a stable and realistic extrapolation (which was no longer the case for natural cubic splines with more knots). In this multinomial model, pairwise Δr values between variants VOC 202012/01, B.1.177 and the category of minority variants were calculated using the emmeans emtrends function as contrasts in the above-average growth rates of each variant (using argument mode=“latent”(47)). Since the growth differences (Δr) in this model were time-dependent, we calculated the average growth difference for the VOC vs. minority variants and for the VOC vs. B.1.177 variant contrasts for the period from November 1 2020 onwards and from July 1st 2020 until the 30th of September 2020, respectively, when each of these variants were actively invading in the population. Second, we also fit a multinomial mixed model in which we included a random intercept for the local-tier local authority (LTLA) and also jointly estimated overdispersion. To allow us to estimate the average growth advantage of the VOC, this model was fit under the assumption of identical and non-time varying selection coefficients across regions, and included NHS region and sample date as additive main effects. This model was fit using the mblogit function of the mclogit R package. The difference in growth rate relative to a particular chosen reference variant was in this model directly inferred from the model coefficients. Finally, the predictions of both models were used to produce Muller plots, to display the change in relative frequencies of the major SARS-CoV2 lineages over time in the UK (Fig. 2C, main text, and Fig. S4).
Rt analysis
For the Rt analysis, we used 4 main sources of data: test positive Covid-19 notifications by UTLA (48), S-gene status from PCR tests by local authority provided by Public Health England (PHE), Google mobility data stratified by context (9), and two publicly available databases of of non-pharmaceutical interventions by UTLA (49, 50). We aggregated the data at the weekly level and restricted the analysis to the period beginning Monday, 5 October.
We calculated the weekly proportion of positive tests that were S-gene negative over time by local authority. We estimated reproduction numbers using the method described in (29) and (31) and implemented in the EpiNow2 R package (51). Daily updated estimates can be downloaded at https://github.com/epiforecasts/covid-rt-estimates/blob/master/subnational/united-kingdom-local/cases/summary/rt.csv. We used two sets of estimates, obtained using uncertain, gamma distributed, generation interval distributions with a mean of 3.6 days (standard deviation (SD): 0.7), and SD of 3.1 days (SD: 0.8) (30) or with a mean of 5.5 days (SD: 0.5 days), and SD of 2.1 days (SD: 0.25 days) (13), respectively.
We then built a separate model of the expected reproduction number in UTLA i during week t starting in the week beginning 14 September 2020 as a function of local restrictions, mobility indicators, residual temporal variation, and proportion of positive tests S-gene negative:
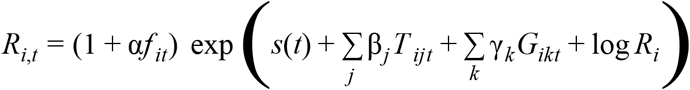where Ri is an UTLA-level intercept corresponding to Rt during national lockdown in November, T ijt is 1 if intervention j (out of: no tiers, tier 1/2/3) is in place and 0 otherwise, Gikt is the relative mobility in context k (home, parks, workplace, etc.) at time t in UTLA i as measured by Google, and s(t) is a time-varying component, modelled either as a region-specific thin-plate regression spline (“Regional time-varying”) or a static regional parameter (“Regional static”). The key parameter is α, the relative change in reproduction number in the presence of the SGTF that is not explained by any of the other variables, where f it is the proportion out of all positive tests for SARS-CoV-2 where the S-gene was tested with SGTF, and the reproduction number in any given UTLA is
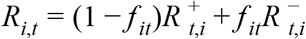where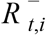 
is the S-gene negative reproduction number,
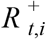is the S-gene positive reproduction number, and it is assumed that
.
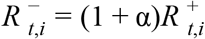We used a Student’s t-distribution observation model with a single variance parameter and a single degrees of freedom parameter. All models were implemented using the brms (52) package in R. All code required to reproduce this analysis is available from https://github.com/epiforecasts/covid19.sgene.utla.rt/.
Analysis of differential age susceptibility for VOC 202012/01 based on secondary attack rates
To determine if there was any difference across age cohorts in susceptibility for the new VOC-202012/01, we analysed the age-stratified aggregated data of secondary attack rates reported by Public Health England (53) using a binomial GLM (Fig. S8). These data comprise secondary attack rates among contact tracing data (from NHS Test and Trace) for the variant of concern (VOC 202012/01), with the identity of strain carried by the index patients (VOC or not) called based on either genomic sequence or S-gene target failure (SGTF) data, and with data split by age bracket of the person that was infected. In total, the dataset contains 17,701 and 456,086 secondary contact records of known age with index patients for which either sequence or SGTF data were available, for the period between 30 November 2020 and 20 December 2020. Out of these secondary contacts, 2,455 and 64,325 became cases, which translates into overall secondary attack rates of 13.87% and 14.10%. To determine the odds ratios for people to be infected by index patients carrying the VOC vs. by those carrying other variants, we fitted a binomial GLM with factors data type (sequence data or SGTF data), age group, variant (VOC or other strains) plus all first order interaction effects. Overdispersion was tested for by fitting an equivalent quasibinomial GLM, but was found to be absent. The R package emmeans was used to make effect plots of marginal and predicted means and carry out Sidak posthoc tests to test if the odds for people to be infected by index patients carrying the VOC was higher than that for those carrying other strains (54) across the different age categories as well as overall. Possible differential age susceptibility was tested for by comparing the log(odds ratios) for people of different age to be infected by the VOC against the average log(odds ratio) for people to be infected by the VOC overall. These age group × variant interaction contrasts were again calculated using the emmeans package, employing a Sidak p value correction for multiple testing. Type III Anova tests were carried out using the Anova function in R’s MASS package.
Details of Bayesian inference
To fit the dynamic transmission model to data on deaths, hospital admissions, hospital bed and ICU bed occupancy, PCR positivity, and seroprevalence for each of the 7 NHS England regions, we performed Bayesian inference using Markov chain Monte Carlo, employing the Differential Evolution MCMC algorithm (55). For each posterior sample, we simulated epidemics from 1 January to 24 December 2020, using data that were current as of 8 January 2021. We used Google Community Mobility data up to 24 December 2020 to capture how interpersonal contact rates changed over the course of the epidemic.
When fitting deaths, hospital admissions, hospital bed occupancy and ICU bed occupancy, we used a negative binomial likelihood with a fitted size parameter for each series and region. For seroprevalence and PCR prevalence, we used a skew-normal likelihood for each data point fitted to produce the same mean and 95% confidence interval as was reported for the data, and took the expected value of the model prediction over the date range during which the prevalence was measured. For fitting to VOC 202012/01 relative frequency over time in the three heavily affected NHS England regions, we used a beta-binomial likelihood with the daily proportion of detected samples that were VOC 202012/01 and a fitted dispersion parameter.
As part of model estimation, we separately fit for each region: the start time of community transmission; the basic reproduction number R0 prior to any changes in mobility or closure of schools; the delay from infection to hospital admission, to ICU admission, and to death; a region-specific relative probability of hospital admission and of ICU admission given infection; the relative infection fatality ratio at the start and at the end of the simulation period, as fatality due to COVID-19 has dropped substantially over time in the UK; a decreasing rate of effective contact between individuals over time, representing better practices of self-isolation and precautions against infection taken by individuals over the course of the year; and coefficients determining the relative mobility of younger people, around age 20, relative to the rest of the population, for the months of July, August, and September onwards. Full details of all fitted parameters, along with prior distributions assumed for each parameter, are in Table S2.
We use two parametric functions extensively in parameterising the model. The first,
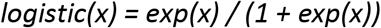is the standard logistic curve. The second,
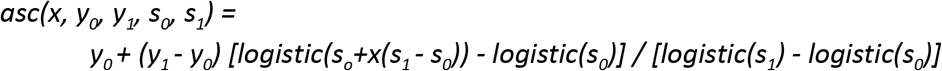is a logistic-shaped curve parameterised to be a smooth S-shaped function of x from 0 to 1, which goes from y0 at x = 0 to y1 at x = 1, with an inflection point at x = −s0/(-s0 + s1) if s0 < 0 and s1 > 0.
Basic epidemiological parameters were broadly informed from the literature and previously reported (11). All parameters that we adopted as assumptions are given in Table S3.
Supplementary Figures
This plot shows the trends in COG-UK sequence counts (A), lineage richness (B), and lineages per-sequence (C) for data downloaded on 2021-01-11. Comparing January 11th download to previous downloads reveals the backfilling of samples from previous sample dates but (D) by 1-month or 31 days prior to a download most of the samples are processed and uploaded to COG-UK. We use data up to 31 days prior to our final download to avoid potential backfilling biases when comparing growth rates across lineages.
Muller plots of the relative abundance of the major SARS-CoV2 lineages (reaching at least 15% in any week overall) in different NHS regions across the UK, based on the raw COG-UK sequencing data, aggregated by week. The remaining minority variants comprise a collection of a total of 440 lineages. Note that the large fluctuations seen in July & August in some regions such as Scotland are caused by low sample size.
Fitted spread of variants to B.1.177 and VOC 202012/01 estimated from a multinomial spline model by NHS region (model 1a in Table S1 and Fig. 2C) with 95% confidence intervals and per-week aggregated raw proportions, shown on a logit (log(odds)) scale. The ca. 3 times faster rate of spread of VOC 202012/01 compared to B.1.177 is apparent (cf. Δr values in Table S1). The excellent linearity on a logit scale for VOC 202012/01 allows us to realistically model the spread of this variant using spatially more fine-grained binomial GLMMs (carried out the level of LTLAs), using a subset of the data from August 1 2020 onwards. Likewise, a binomial GLMM was used to model the spread of variant B.1.177 for the period between July 1 2020 and September 30 2020, before it starting to be displaced by VOC 202012/01.
Muller plots of the relative abundances of the major SARS-CoV-2 variants in the UK, based on a multinomial mixed model fit to COG-UK sequence data, incorporating lower-tier local authority as a random intercept as well as overdispersion (common-slopes multinomial mixed model 1b in Table 1). A model extrapolation until the end of January is shown (shaded area). Minority variants are 440 circulating SARS-CoV-2 strains that never reached >15% in any week overall.
Binomial GLMMs with separate-slopes by region (models 2b and 2g in Table S1) show that VOC 202012/01 has been displacing all other SARS-CoV2 at a near-constant rate across different regions in the UK (A), with pairwise Tukey posthoc tests for differences in slopes across regions only demonstrating a slightly slower rate of displacement in the East of England vs. in the North East and Yorkshire (z ratio = −3.68, P = 0.007, all other P > 0.05). In addition, a common slope model with a constant rate of spread in different regions had a better BIC value (model 2a in Table S1). By contrast, variant B.1.177, which in the UK became the major strain at the end of September, had a much lower competitive advantage in comparison with the minority variants that it displaced, evident from a ca. 3 times lower slope on a log(odds) scale (Table S1). In addition, pairwise Tukey posthoc tests for differences in slopes across regions demonstrate significant cross-regional variation in the rate of spread of this variant (12 out of 36 pairwise comparisons with P < 0.05), and a model with separate slopes per region provided the best fit based on the BIC criterion. This supports the idea that VOC 202012/01 enjoys a consistent competitive advantage, whilst the small competitive advantage enjoyed by variant B.1.177 may have been largely, though perhaps not exclusively, the result of stochastic introduction events, e.g. linked with travel to Spain (42), where it was first observed.
Independent estimate of the rate at which VOC 202012/01 is displacing other variants based on the random sequencing of SARS-CoV2 strains in Denmark, reported on an aggregated per-week basis (56) (for week 39 of 2020 until week 1 of 2021). A binomial GLMM with a common slope across regions and an observation-level random effect to take into account overdispersion fitted the data best, based on the BIC criterion, and resulted in an estimated selection rate Δr of 0.10 [0.07, 0.12] 95% CIs (Table S1, model 3a). In addition, a model with separate slopes per region showed that there were no significant differences in the slopes and implied rates of spread across regions (pairwise Tukey posthoc tests for differences in slope, all P > 0.05).
Estimates of the rate at which VOC 202012/01 is displacing other variants across Denmark and the UK, based on a joint fit of the per-week aggregated data from both countries. A binomial GLMM with separate slopes per country but identical slopes per region nested within country provided the best fit based on the BIC criterion, resulting in selection rates Δr estimated for Denmark and the UK of 0.08 [0.07, 0.10] 95% CIs and 0.11 [0.10, 0.12] 95% CIs, respectively (Table S1, model 3b). The rate by which the VOC displaces resident variants was slightly but significantly lower in Denmark than in the UK (z ratio = 2.60, 2-sided P = 0.009), but this might be due to the presence of other resident strains in Denmark than in the UK.
Analysis of age-stratified secondary attack rates, based on data reported by Public Health England (57) (data derived from the COG-UK dataset, the PHE Second Generation Surveillance System and NHS Test and Trace). A binomial GLM with data type (sequence data or S-gene target failure), age group of the person being infected, and variant (VOC 202012/01 or not) plus all first order interaction effects shows that the odds to be infected by an index patient carrying the VOC is consistently higher than by those carrying other variants (A). Sidak posthoc tests show the odds to be infected by the VOC to be significantly greater than by a non-VOC variant for nearly all age groups (for all age groups and both data types 2-sided P < 1E-7, except for 80+ where P = 0.07 and 0.06 for sequencing and SGTF data, respectively). The mean probability for secondary contacts to become infected in function of age was not significantly different across both types of data (no significant data type by age interaction effect, Type III test, 
) and there was also no difference in the estimated increased odds to be infected by a VOC vs. a non-VOC index patient (no significant data type by variant interaction effect, Type III test, 
). The mean odds ratio to be infected by an index patient carrying the VOC vs. a non-VOC variant across all age groups and both data types was 1.41 [1.34, 1.48] 95% CIs. The relative susceptibility to be infected by the VOC showed little variation in function of the age of the person being infected, with only the 40-49 category being slightly more susceptible to be infected by a VOC vs a non-VOC carrying index patient than average (measured in terms of difference in log odds ratios, Sidak age group x variant interaction contrasts, z ratio = 3.45, P = 0.01, all other P > 0.05).
Subscripts for age group and region are omitted from this diagram and only certain key parameters are shown. Compartments and processes in purple apply to the vaccine model only. S, susceptible; E, exposed; L, latent (see below); IP, preclinically infectious; IC, clinically infectious; IS, subclinically infectious; R, recovered; V, vaccinated. Subscript 2 represents compartments and parameters for VOC 202012/01. Above, λ and λ2 are the force of infection for preexisting variants versus VOC 202012/01; y and y2 are the fraction of cases that develop clinical symptoms for preexisting variants versus VOC 202012/01; v is the rate of vaccination; wv is the waning rate of vaccination (assumed to be zero for this manuscript); p captures cross-protection against VOC 202012/01 conferred by immunity to preexisting variants; q captures vaccine protection against disease; and r captures vaccine protection against infection. L and L2 are additional compartments for a latent period prior to subclinical infection only (i.e. with zero probability of clinical infection). For a vaccine with efficacy against disease ed (e.g. ed = 0.95 for this manuscript) and efficacy against infection ei (e.g. ei = 0.6 for this manuscript), we assume r = (1 – ei) * ed and q = (1 – ei) * (1 – ed).
Model posterior densities for the “increased transmissibility” model for seven NHS England regions. See Table S2 for parameter definitions.
Model posterior densities for “longer infectious period” for three NHS England regions. See Table S2 for parameter definitions.
Model posterior densities for “immune escape” model for three NHS England regions. See Table S2 for parameter definitions.
Model posterior densities for “increased susceptibility in children” model for three NHS England regions. See Table S2 for parameter definitions.
Model posterior densities for “shorter generation time” model for three NHS England regions. See Table S2 for parameter definitions.
Model posterior densities for a “combined” model with increased transmissibility, altered serial interval, immune escape, and altered susceptibility in children. See Table S2 for parameter definitions.
Contrasting (A) longer infectious period and (B) increased susceptibility among children models. Measured from infections in the fitted model between 1 November and 15 December 2020 in the South East NHS region..
Fit of “increased transmissibility” model to data up to 24 December 2020. Black lines show observed data, while coloured lines and shaded regions show median and 95% credible intervals from the fitted model.
Fit of “increased transmissibility” model to data up to 24 December 2020, with the emergence of the second strain (VOC 202012/01) disabled. Surges in the East of England, London, and the South East are no longer captured. Black lines show observed data, while coloured lines and shaded regions show median and 95% credible intervals from the fitted model.
Fit of a model with no second strain up to 24 December 2020. The model increases transmission of the original strain to compensate, but cannot capture surges in the East of England, London, and the South East. Black lines show observed data, while coloured lines and shaded regions show median and 95% credible intervals from the fitted model.
Google Mobility indices used for projections in the main text (Fig. 4).
Model projections by NHS region, without vaccination. Median and 95% credible intervals are shown. See Fig. 4A, main text.
Model projections by NHS region, with 200,000 vaccinations per day. Median and 95% credible intervals are shown. See Fig. 4B, main text.
Model projections by NHS region, with 2 million vaccinations per day. Median and 95% credible intervals are shown. See Fig. 4C, main text.
Supplementary Tables
Models marked with an asterisk are those given in Table 1.
Compare to Table 2, main text.
Footnotes
Note, 6 February 2021 — Recent analysis conducted by LSHTM and other groups has identified an increase in mortality associated with community-tested infections by VOC 202012/01 (https://www.gov.uk/government/publications/nervtag-paper-on-covid-19-variant-of-concern-b117). This preprint, which assesses the transmissibility and severity of VOC 202012/01 using data up to 24 December 2020, finds that these early data are compatible with a range of possibilities from a small decrease to a moderate increase in severity associated with the new variant. Scientific understanding of the severity of VOC 202012/01 will continue to improve as new data become available.
Added statistical analyses of growth rate of VOC 202012/01; added additional hypothesis for increased growth rate of VOC 202012/01.
References
