Abstract
Interactions between humans cause transmission of SARS-CoV-2. We demonstrate that heterogeneity in human-human interactions give rise to non-linear infection networks that gain complexity with time. Consequently, targeted vaccination strategies are challenged as such effects are not accurately captured by epidemiological models assuming homogeneous mixing. With vaccines being prepared for global deployment determining optimality for swiftly reaching population level immunity in heterogeneous local communities world-wide is critical. We introduce a model that predicts the effect of vaccination into an ongoing COVID-19 outbreak using precision simulation of human-human interaction and infection networks. We show that simulations incorporating non-linear network complexity and local heterogeneity can enable governance with performance-quantified vaccination strategies. Vaccinating highly interactive people diminishes the risk for an infection wave, while vaccinating the elderly reduces fatalities at low population level immunity. Interestingly, a combined strategy is not better due to non-linear effects. While risk groups should be vaccinated first to minimize fatalities, significant optimality branching is observed with increasing population level immunity. Importantly, we demonstrate that regardless of immunization strategy non-pharmaceutical interventions are required to prevent ICU overload and breakdown of healthcare systems. The approach, adaptable in real-time and applicable to other viruses, provides a highly valuable platform for the current and future pandemics.
Main
As the COVID-19 pandemic is spreading around the world it is inflicting multi-dimensional damage to humanity. Now, a year into the pandemic it is evident that traditional epidemiological and public health interventions alone are not capable of eliminating the spread of SARS-CoV-2 without insurmountable socio-economic and human costs. However, as of early december 2020 there are 3 major vaccine candidates expected to be deployed before New Year1. Whilst these vaccines each seem to offer effective protection against the virus their roll-out constitutes the single largest product launch in human history. Limits on production and distribution renders it absolutely necessary to prioritize and structure the deployment2–4. Furthermore, the European Commission recently concluded that “the successful deployment and a sufficient uptake of such vaccines is equally important” rendering it critical to be able to “monitor the performance of the vaccination strategies”5.
Human-human interaction networks (HHIN) are formed by physical proximity between individuals in time and space and depend on the typical or exceptional behavior of humans (Fig. 1a). Respiratory diseases, such as COVID-19 (Coronavirus Disease 2019), can spread within such HHIN by defining a sub-network of infection emitters and receivers, iHHIN (infection HHIN). These networks are stochastic and evolve over time in a non-linear manner. Consequently, the spread of SARS-CoV-2 in the population is a complex system and must be analyzed accordingly.
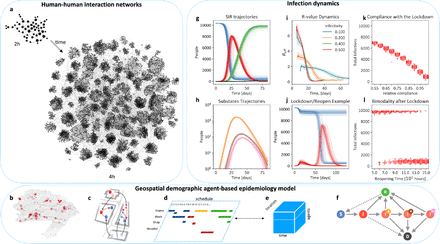
a, Human-human interactions create dynamic stochastic networks in space and time. b, The model uses data of real-world communities with annotated buildings, demography, and statistics on daily occupations (Movie 1). c, Individuals move between locations to meet other individuals, d, Schedules define typical behavior and where-abouts of individuals. e, Individuals, locations, and time span a multidimensional space for stochastic simulations. f, An individual’s health status can be susceptible - S, infected - I, recovered - R, deceased - D, and infection sub-states a- or presymptomatic (plain I), diagnosed (Id), hospitalized (IdH), in intensive care (IdICU). g, Simulation of uncontrolled baseline scenario for a town (here German town Gangelt with 10.351 individuals), starting from 4 infected individuals; dynamics of states S, I, R, and D over approx. 12 weeks (100 replicates, colors as in f). h, Dynamics of I, Id, IdH, and IdICU (colors as in f). i, The R-value as emergent model property for different values of the model parameter infectivity, which may change with interventions such as mask wearing or keeping distance. j, Simulated performance of an intervention: lockdown (8 days after first infection) and reopening (after 5 weeks). k, Compliance (in % of population) with the lockdown leads to less total infection. l, Bimodality: whether lockdown and reopening lead to high or low infection numbers depends on the reopening time. For a range of reopening times, high/low I are obtained in a certain ratio, indicating uncertainty in the outcome.
Thus, to accurately and timely predict the trajectory of the disease in real-world scenarios, the epidemiological community has already pleaded for new types of models that include motion of individual humans and their heterogeneous behavioral patterns, time-dependent infectivity as well as the effect of non-pharmaceutical and pharmaceutical interventions such as vaccination6,7. Here, we provide a theoretical quantitative framework for precision simulation of spatio-temporal SARS-CoV-2 transmission and demonstrate its use in determining optimality in different vaccination strategies.
Heterogeneous model of human-human interaction and COVID-19 infection networks
To keep model complexity reasonable and yet accurately capture human behavior, we developed a detailed agent-based geospatial model8, where every agent represents a human individual within a realistic community (Fig. 1). We complemented a classical SIR model with the clinically described stages of SARS-CoV-2 infection9 and COVID-19 disease and incorporated georeferenced information10, demographic data11 and realistic daily schedules (full description in Supplementary Methods section X, Supplementary fig. 1-26, Supplementary Tables 1-26). This enables us to reflect the current state of the pandemic and to simulate realistic scenarios within concrete human populations; the respective HHIN and iHHIN can be reconstructed from the simulations (Fig. 1a).
To reduce complexity of the HHIN, each human individual is associated with a specific physical location at each time point. These locations are specific for the community such as homes, work places, schools, hospitals, and public places12 (Fig. 1b). The entire population is initialized with demographic census data resulting in representative age distributions and household compositions. An individual is defined by its household, age, weekly schedule, and health status. The schedule specifies the individual’s presence in different locations (Fig. 1c-e). Schedules change with health state and imposed interventions. The health states for individuals are defined as: susceptible (S), infected (I), recovered (R) or deceased (D). Infected individuals (I) can obtain sub-states specifying their condition as pre- or asymptomatic (plain I), diagnosed (Id), hospitalized (IdH), or being in an ICU (IdICU) (Fig. 1f). During simulations, individuals’ health states, presence at locations, interactions with other individuals and infection transmissions are recorded at each time step. This makes the stochastic HHIN and iHHIN traceable and amenable to theoretical analysis and implementation of different intervention strategies such as vaccination. In order to evaluate the effect of (non-)pharmaceutical interventions, we simulated a baseline scenario representing an uncontrolled outbreak (Fig. 1g,h). The history of infection events defines the basic reproduction number (R-value), and is thus an emergent property of our model (Fig. 1i). The R-value also depends on the infectivity, which can be reduced by general interventions such as protective gear, hygiene and social distancing. Non-pharmaceutical interventions modify the infection dynamics, exemplified for lockdown and reopening (Fig. 1j, Supplementary Figures S10-S15). Also the level of compliance in the population with interventions influences their effect, e.g. on infection numbers in a manner consistent with reality (Fig 1k, Supplementary Fig. 9). Importantly, simulations of specific interventions reveal bimodality, i.e. lead to qualitatively different outcomes (the infection ceases in some simulations, while generating a strong second wave in others, Fig. 1l).
The HHIN comprise three different classes of interactions, namely those that: (i) cannot lead to transmission of infection (e.g. between two S or between two I), (ii) can potentially result in transmission (interaction between S and I without successful transmission), and (iii) result in transmission of infection from I to S, which defines the iHHIN (Fig. 2a).
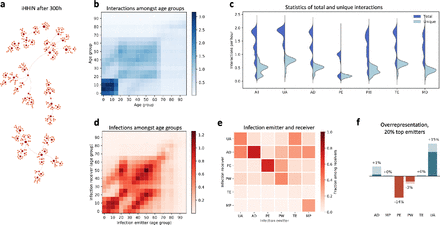
a, Infection networks in the modeled community unfolding within 300 hours. b, Heatmap of daily interactions between age groups exhibiting overrepresentation of interactions among underaged and within families. c, Distributions of total and unique interactions for individuals with different occupations. d, Heatmap of daily infection numbers between age groups for the baseline scenario. e, Likelihoods to transmit the infection from emitters to receivers sorted by occupation. f, Overrepresentation of occupation groups in infection transmission (number of receivers within the group relative to average number of receivers). UA - Underaged, AD - adults (age groups 20-65 excluding PW, MP, and TE), PW - public workers, MP - medical professionals, TE - teachers, PE - pensioners.
The HHIN and iHHIN are age- and occupation dependent. Analysis of age-specific interaction patterns reveals strong interactions within households, indicated by overrepresentation of interactions within and between adjacent age cohorts (partnerships) and parent-child related age-cohorts (Fig. 2b, center and off-center diagonals). Underaged individuals, as well as the working population, show stronger interaction with members of the same group, as apparent from rectangular interaction patterns representing school and workplaces. This resembles real-world interaction patterns14,15, but strongly differs from homogeneous mixing models (Supplementary material). The distribution of interactions per occupation reveals that underaged in general have more interactions than others, even than public workers (Fig. 2c).
As a consequence, infection transmission in the baseline scenario reflects the interaction patterns yielding high infection transmission numbers within households and within the group of underaged, medium infection transmission between working adults and lower infection rates among pensioners, when sorted by age (Fig 2d). Sorting infections according to occupation uncovers that underaged most likely infect other underaged and adults, while adults predominantly emit to other adults, and pensioners mostly infect each other. However, public workers emit towards other public workers and pensioners and, hence, create an infection hub between the groups (Fig. 2e). We also find that underaged are significantly overrepresented as emitters, followed by adults, while pensioners are underrepresented (Fig. 2f). Public workers are slightly underrepresented as emitters, while teachers and medical professionals belong to the average. These interaction and infection patterns can change significantly when non-pharmaceutical interventions are applied (Supplementary material).
The stochasticity within the iHHIN can be recognized from the impact of an individual infection event, which may either not give rise to further infection events or further grow the network. We observed that 70% of infections originate from only 20% of the infected population and that 70% do not spread the infection further, which agrees with the Pareto-principle13. The iHHNI exhibits emergent patterns, which help to understand infection spread and provide a basis to efficiently interrupt infection transmission, as discussed below.
Quantifying the performance of targeted immunization strategies
Vaccination of the human population against COVID-19 is considered the single largest product launch in human history. This immense logistical challenge necessitates careful prioritization in order to swiftly reach maximal suppression of the disease and also save lives16. Given that effective vaccines are becoming available soon, but not for everybody at the same time, we can now use the model that has been trained for different communities and for different non-pharmaceutical intervention scenarios (supplementary material) to predict the effect of pharmaceutical intervention scenarios. To this end, it is critical for the community to define which specific objective applies when searching for optimal targeted immunization strategies4. Here, we analyze three alternatives: (i) minimize the number of fatalities, (i) reduce the number of infections in total or in a period of time, and (iii) reduce the number of hospitalizations or individuals requiring intensive-care treatment to prevent a collapse of the health system.
We simulated seven scenarios for different fractions of vaccinated individuals (Fig. 3) obtaining the ratio of infected individuals (Fig. 3a), the proportion of fatalities (Fig. 3b), the likelihood of an emerging infection wave, which also provides a measure for the robustness of strategy against infection waves (Fig. 3c), and the maximum number of individuals simultaneously requiring an ICU (Fig. 3d).
Comparison of strategies using different selection criteria for the vaccination of individuals: “random” - randomly selected individuals, “forecasted” - individuals forecasted to be infected in a pre-simulated baseline scenario, “overrepresentation” - groups overrepresented as emitters (Fig. 2f), “interaction” - by interaction frequency starting with the highest, “household” - per household starting with one inhabitant at a time, “age” - by age starting with the oldest, and “combined” - first elderly people (>60 yrs) subsequently by interaction frequency. In all cases, fractions between 0.5 and 0.9 of the population have been set to be vaccinated according to the applied criteria at the starting point. a, Fraction of infected people over the time course (relative to the remaining number of susceptible at start), b, Fraction of deceased (relative to susceptible at start). c, Fraction of simulation runs, which exhibited an infection wave (l> 80 subsequent infections) after the vaccination. d, Maximum number of individuals requiring simultaneously an ICU at some point in time during the simulation. The black line indicates the capacity of ICU beds (assuming the German number of roughly 30.000 per 82 million inhabitants). A,B,D) Lines and shaded area represent mean values and confidence intervals, respectively (CI=95%, N=100).
For high vaccination levels (here more than ⅔ of the population immunized), the strategy to vaccinate the most interactive individuals first is most effective for all three objectives. For lower vaccination levels, we identify a clear tradeoff between different strategies depending on the objective, i.e. attenuation of the infection wave, preventing fatalities, or avoiding ICU overload. Aiming for a reduced number of infections, it is most effective to vaccinate the most interactive individuals first, as it reduces the probability for an emerging infection wave, and thus increases systemic robustness. It outperforms vaccination by forecasting of infected individuals in a pre-simulated baseline scenario. Random vaccination underperforms compared to the other two strategies, in agreement with6,17, but outperforms household-wise and sorted-by-age vaccination. Group-wise vaccination according to the overrepresentation in the infection dynamics performs near average. While most strategies reduce the fraction of infection down to zero at 90% vaccination or lower, this is not achieved by age-sorted vaccination. The reason is that young individuals always keep interacting, leading to infection spread among the remaining susceptibles; infection networks never fully dissolve. Individuals of similar age frequently form sub-networks that remain unperturbed by vaccination of other individuals who do not belong to that same age group.
To reduce fatalities, the age-sorted strategy is very effective at low vaccination levels and outperforms all other strategies significantly (Supplementary Fig. 22). However, for the high vaccination levels at which other strategies display population level immunity, those other strategies surpass vaccination by age (first the interactives, then the forecasted and random strategies), since this strategy is not able to suppress deaths completely before 100% population level immunity is reached. Interestingly, for low to average levels of immunization also the per-household strategy is effective in reducing the death toll. This is due to the fact that elderlies who are more likely to die from COVID-19 typically live in households of 1-2, and thus profit early from this strategy. Note that the strategy to immunize by overrepresentation leaves the other groups fully susceptible, which leads to the bumpy infection and death curves. The “combined” strategy integrates the two strategies that either best reduce infections (i.e. by interaction) or death toll (by age), however it outperforms neither.
The simulations also clearly reveal a problem of strategies that focus on vaccination only (Fig. 3d): with the objective to reduce the occupancy of ICUs, vaccination by age performs best at less than ∼58% but vaccination by interactivity is best above this level. However, below 63% vaccination, none of these strategies is able to prevent overload of ICU capacity, without additional non-pharmaceutical interventions. Importantly, our model has not implicitly included an increased death rate if ICUs are overloaded. Hence, the death toll would be even higher than predicted if ICU demands cannot be met. While the ICU capacities may vary in different locations, the problem remains that ICU demand and capacity differ widely for all strategies at stages of partial vaccination. This implies that non-pharmaceutical interventions should be considered to accompany the vaccination process in order to prevent the collapse of the healthcare system.
In conclusion, there is not a single number for the vaccination percentage ensuring population level immunity. Instead, this number depends entirely on the chosen strategy, i.e. according to age, interactivity and occupation of the already vaccinated or recovered individuals. Importantly, it also depends both on the heterogeneity of the population and on the specific virus, its virulence and infectiousness. In particular, lower infectivity will decrease the required vaccination coverage to achieve population level immunity (Supplementary Fig. 23). Recently, it was demonstrated that >70% of a population can be infected during an uncontrolled outbreak, which is above the reported theoretical population level immunity threshold for SARS-CoV-218. These observations are supported by the values our model predicts.
As long as we cannot ensure vaccination of about ⅔ of the population, it is not possible to serve all objectives to reduce deaths, ICU demand and infection levels at the same time equally well. Above this value, vaccination of individuals sorted by their interactivity shows to be most successful for all three objectives.
Since vaccination is not mandatory in most countries, high levels of vaccination of the population can only be reached if most people volunteer. Lack of commitment of the population would be partially comparable to lack of compliance to lockdown interventions (Fig. 1k): if 25% of the population refuse vaccination (irrespective of the reason), the effects are similar to non-sufficient dose numbers with the same strategy-dependent effects on infection spreading, ICU overload, or fatalities.
Discussion
Our work is timely and enables data-driven geospatial-temporal, stochastic, individualized network-based evaluation of the integrated impact of human endeavours to quantify non-linear effects of non-pharmaceutical intervention scenarios and optimality in targeted immunization strategies. It suggests that the COVID-19 infection network is a sparse small network (iHHIN) compared to the overall population interaction network (HHIN). Thus, models based on homogenous mixing or averaging statistical models are likely to be of limited use19,20 since they fail to capture nonlinearity and complexity emerging from stochastic and sparse events influenced by individual human behavior as has been pointed out previously21–24. Remarkably, the heterogeneous model offers insight into the bimodal behavior of SARS-CoV-2 infection dynamics and demonstrates that effective interventions require strict execution (stringency) and careful temporal control (timing).
A general limiting factor in disease modelling, which also holds true for this work, is that the transition probabilities for the propagation of e.g. COVID-19 are intrinsically incomplete and evolving (Supplementary Table 24,25–29). A caveat in our study is the setting of relatively small European communities with a limited number of schools, work- and public places. Another limitation of the current version of our approach is that it does not entail inter-community transport (travel) nor immunization of travelers, as has been suggested to be made mandatory by some airlines and may reduce epidemics30. Nevertheless, as we show that human interaction and infection transmission creates dynamic stochastic networks which should be exploited to fight the pandemic. Consequently, the optimization of vaccination strategies can be supported by network-based, location- and situation-specific analysis. We demonstrated that there is a tradeoff between different strategies for low levels of vaccination (vaccination by age minimizes fatalities, while vaccination by interactivity reduces infection events). However, at high vaccination coverage, vaccination by interaction prevails. It is important to note that the vaccination level giving rise to population level immunity is not a unique number but depends on the vaccination strategy. Our conclusions depend on the demographic structure and the heterogeneity in the interaction patterns and it can be assumed that the stronger the heterogeneity in interactions the better vaccination by interaction will perform. In summary, the situation remains complex and not fully predictable, e.g. due to bimodality/multimodality of intervention outcomes.
Practically, to implement the strategy by interaction one could exploit the information that tracing apps collect on mobile phones for simulation-based governance. Targeted immunization in the midst of an ongoing outbreak likely performs differently, since infection spreading might already reach the vulnerable subgroups and spread further in their subnetworks. Vaccination of the population is a process in time, especially in the global context. But locally, significant vaccination coverage may be achieved fast in some countries or towns. The optimal vaccination strategy depends on the supply of vaccines, the demographic structure, local behavioral costumes, and the capacity to realize the specific strategy. This coincides with the statement by the European Commission that the objectives of such strategies have to be “in the beginning on decreasing death rates and disease burden from the COVID-19 pandemic and ensuring the continuation of essential services, later in the vaccination deployment process this may shift to the reduction of wider societal and economic restrictions and impact. Such flexibility in terms of changing objectives should be envisaged by countries when preparing their vaccination strategies”5. In future, forecasting of the effect of vaccination shall be combined with prior simulation of the ongoing surge of infections and the effect of hitherto applied non-pharmaceutical interventions to precisely cover the situation in specific communities at the time when a vaccine becomes available.
In a post-covid world it is clear that communities and governments world-wide require smarter and real-time based simulation support for conducting governance for keeping research, education, economies and society functional during disease outbreaks by minimizing lockdowns, travel bans, civil non-compliance and catastrophic socio-economic impact of non-pharmaceutical interventions. To achieve this new paradigms for modeling of infection networks that capture the nonlinear complexity and stochasticity will be important, beyond targeted immunization strategies. Finally, the public could also be better prepared through education. From a philosophical point of view it may be helpful to encourage John Nash inspired self-governance of citizens so they realize that within a society, individuals are best off if they make the best decision they can, taking into account the decisions of other individuals.
Methods
The concept of geospatial demographic heterogeneous agent-based model, the estimation of parameters for the stochastic transitions between states, and details of the simulations are detailedly represented in the Supplementary materials.
Data Availability
All data used are included in the supplementary material.
Funding
This work was supported by the Deutsche Forschungsgemeinschaft (DFG: Cluster of Excellence MATH+, TRR 175) and by the German Ministry of Education and Research (BMBF, Liver Systems Medicine (LiSyM) network grant) and by the People Programme (Marie Skłodowska-Curie Actions) of the European Union’s Horizon 2020 Programme under REA grant agreement no. 813979 (‘Secreters’). XEF is supported with a postdoctoral grant from CONACYT (CVU 420248). RL is supported by a BMBF GO-Bio initial grant 031B0988.
Author contributions
Conceived the project: RL, EK. Conceptual work on the model: BG, SOA, OB, JAHW, XEF, RL, EK. Programming: BG, SOA, OB, JAHW, AK, LB, JELH, MKa, RMT, MS. Analysis and computational experiments: BG, SOA, OB, JAHW, XEF, AK, MKa, RMT, MS, EK. Data collection: XEF, JELH, MKb, LM, HP, PSS. Wrote the paper: BG, OB, JAHW, XEF, MKb, MS, RL, EK. All authors agreed on the final version of the manuscript.
Competing interests
Authors declare no competing interests.
Data and materials availability
All data is available in the main text or the supplementary materials.” The code is available at https://tbp-klipp.science/GERDA/code/
SUPPLEMENTARY MATERIALS
Materials and Methods
Figures 1-26.
Tables 1-26.
Movie 1.
ACKNOWLEDGMENTS
We wish the populations of Gangelt, Heinsberg, Epping, and Vaxholm all the best and would like to point out that the model remains an abstraction and it is neither a repetition of history nor can it be traced back to real individuals, thus safe-guarding the privacy of the public.