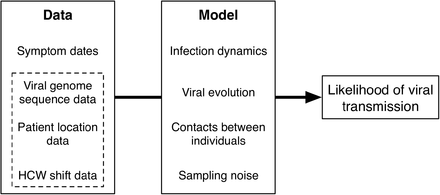
Abstract
Identifying linked cases of infection is a key part of the public health response to viral infectious disease. Viral genome sequence data is of great value in this task, but requires careful analysis, and may need to be complemented by additional types of data. The Covid-19 pandemic has highlighted the urgent need for analytical methods which bring together sources of data to inform epidemiological investigations. We here describe A2B-COVID, an approach for the rapid identification of linked cases of coronavirus infection. Our method combines knowledge about infection dynamics, data describing the movements of individuals, and novel approaches to genome sequence data to assess whether or not cases of infection are consistent or inconsistent with linkage via transmission. We apply our method to analyse and compare data collected from two wards at Cambridge University Hospitals, showing qualitatively different patterns of linkage between cases on designated Covid-19 and non-Covid-19 wards. Our method is suitable for the rapid analysis of data from clinical or other potential outbreak settings.
Introduction
Having emerged via zoonotic transfer in late 2019, the COVID-19 pandemic remains an ongoing public health priority [1,2]. Understanding the nature of viral transmission is a key factor in all strategies to prevent and control disease spread. The earliest stages of the outbreak were characterised by small, localised clusters of infection [3,4]. Identifying chains of linked cases remains crucial for containing disease spread [5,6], particularly in healthcare settings. Outbreaks in these settings, however, provide a particular challenge to the identification of linked cases as regular new introductions from the community have to be distinguished from potential cases of nosocomial transmission [7–9].
Viral genome sequencing provides one strategy for identifying clusters of transmission. The rapid evolution of viral populations leads to the accumulation over time of genetic differences which distinguish linked from unlinked cases [10]. A broad range of phylogenetic approaches for identifying linked infection clusters have previously been described [11–15]
With this background, a recent study of hospital-based COVID-19 infection used genome sequencing to identify potential clusters of infection. In this study, sets of individuals with identical viral genome sequences were often verified by a process of epidemiological follow-up to correspond to likely cases of nosocomial transmission [5]. Data from genome sequencing allowed feedback in real time to clinical, infection control and hospital management teams to inform their response.
Whilst genome sequence data is of great value for studying viral transmission, it has some drawbacks in the context of SARS-CoV-2. Given the recent emergence of SARS-CoV-2, and the low diversity of global viral sequences, finding identical sequences in different individuals does not necessarily imply a connection between those people. Furthermore, sequence data is not the only type of information that may be available. For example, studies of known SARS-CoV-2 transmission events have quantified the distribution of times between the onset of symptoms and the transmission of the virus, and of the subsequent time between infection and the onset of symptoms [16–19]. In addition the contribution of asymptomatic individuals to transmission is difficult to ascertain as they may not be sampled [20,21]. Such information has implications for the retrospective analysis of potential transmission events. Information about the location of individuals might also contribute to the identification or ruling out of connections; people who never physically interact cannot directly transmit the virus from one to another. Potential, therefore, exists for novel approaches in the identification of transmission clusters.
New methodologies have the potential to gain insights into viral sequence data. For example, noise in the process of viral sequencing can affect phylogenetic analyses which rely on finding identical sequences. Multiple studies have considered the problem of noise in genome sequence data, particularly with regard to identifying variant frequencies [22–25]. The potential for error in variant frequencies means that a viral consensus sequence is also stochastic, since it is generated from a potentially diverse viral population. Further, evolution would be expected to change viral sequences over time. Metrics which account for measurement error and viral evolution may be advantageous for identifying linked cases of infection.
A variety of studies have used short-read viral sequencing to evaluate the nature and likely direction of viral transmission. The ability of such data to capture the diversity of within-host viral populations has proved very valuable in the assessment of transmission events [26–29]. However, the low cost of data collection via nanopore-based methods has often outweighed the additional precision provided by Illumina technology [30,31]. Analyses which can utilise the consensus sequences provided by such methods have broader application, increasing their value.
Here, we describe a tool which implements a combined statistical and evolutionary framework to analyse genome sequence data with location data and knowledge of SARS-CoV-2 infection dynamics to rapidly identify clusters of infection. Our approach provides a rapid data analysis, outputting information in an easily interpretable format. We demonstrate its use with augmented sequence data from outbreaks on hospital wards, illustrating the value of different kinds of data in this context. While designed with clinical application in mind, the generality of the properties of viral transmission make our method applicable to any setting in which appropriate data has been collected from more than one individual. We hope that our approach will be of value in ongoing public health efforts to combat the COVID-19 pandemic.
Results
Our method exploits data from genome sequencing alongside other information about individuals and COVID-19 infection. A key parameter in our model is the extent to which a consensus viral genome sequence is subject to error. Where viral sequence data is collected on multiple occasions during the course of a single infection, regression models may be used to estimate both the rate of viral evolution and the extent of noise in a single sample [32].
We therefore examined cases among data collected from patients at the Cambridge University Hospitals National Health Service Foundation Trust (CUH) for which more than one viral sample was sequenced. A total of 136 such patients were identified, with between 2 and 9 (median 2) samples collected from each individual and 336 samples in total. Intervals between pairs of samples varied from 0 to 39 days. Each sample gave rise to a consensus sequence. We filtered the data to remove sequences with less than 90% coverage of the genome. Combining these data through regression, we inferred a mean error rate of approximately 0.207 nucleotide errors per sequence (Supporting Figure 1). While small, this rate is significant. In our model, the expected time between symptoms being reported from individuals in a transmission pair is 5.7 days; the expected amount of sequence evolution within this time is not greater than the expected difference between two sequences resulting from noise (Supporting Figure 2).
Our approach estimates the likelihood that transmission could have occurred between pairs of individuals. The model takes as input dates on which individuals became symptomatic for COVID-19 infection. Further data which can be considered includes viral genome sequence data, and time-resolved location data for each individual. Our model combines details of COVID-19 infection dynamics with a model of viral evolution, information about potential contacts between individuals, and measurement error in the sequence data. Increasing amounts of data provide increasing amounts of resolution about the potential for viral transmission.
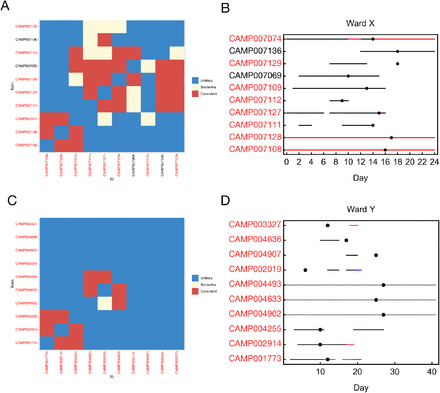
A. Output from the a2bcovid package given data from ward X. The plot shows potential links between infections. Identifiers of individuals are coloured in either black (patients) or red (HCWs). Squares in the grid indicate that transmission from one individual to another is consistent with our model (red), borderline (yellow) or unlikely (blue). B. Locations of individuals linked to the ward X outbreak. Black lines indicate presence on ward X. Red lines indicate known household contacts between three individuals. Dots show times at which individuals first reported symptoms. C. Output from the a2bcovid package given data from ward Y. D. Locations of individuals linked to the ward Y outbreak. Black lines indicate presence on ward Y. Red and blue lines show presence in locations other than ward Y.
For each pair of individuals in a dataset our model compares the input data with an underlying model of transmission, calculating a likelihood value for transmission having occurred in each direction. These likelihoods are then assessed against a precomputed scale to produce an indication of whether the data are consistent with a transmission event (nominally representing a p-value > 0.05), whether they are borderline (nominally having a p-value between 0.05 and 0.01) or unlikely given our model (nominally equivalent to a p-value < 0.01). We applied our model to data from two wards within CUH, which we term X and Y. Ward X was a ‘green’ ward, used for patients considered to be free from COVID-19 infection. By contrast, ward Y was a ‘red’ ward within the hospital, designated for the treatment of patients with COVID-19 infection, on which multiple cases of infection in healthcare workers (HCWs) were identified. Information collected for these individuals included genome sequence data from viral swabs, dates of symptom onset and dates on which individuals were present on the wards in question. Our method combines multiple types of data, using the information available to provide an insight into potential links between cases of infection (Figure 1). We conducted two analyses of the data from wards X and Y, the first looking at the complete data collected for individuals, including dates of symptom onset, viral genomes and location data, and the second excluding location data, considering only times of symptom onset and the viral sequence data.
Analysing the complete data collected from each ward gave an estimation of the likelihood of transmission from each individual in the dataset to every other (Figure 2). These likelihood values are asymmetrical. For example, the data is consistent with transmission from 7069 to 7074 having occurred, but transmission from 7074 to 7069 is unlikely. This is in part explained by 7069 reporting symptoms four days before 7074; the order of reporting symptoms provides information on the likely direction of transmission. Data from ward X suggest that the ten infections for which data were available were mutually connected, though with some underlying structure to the outbreak. In particular the bottom three individuals 7108, 7128, and 7074, could each mutually have infected each other, but have only borderline chances of having infected anyone else on the ward. These individuals could have been infected by either 7069 or 7112 infecting 7074, leading to further transmission within that cluster. The remainder of the individuals on the ward show multiple plausible transmission events, though we note that 7129 has only a borderline probability of having infected any other person. Examination of location data collected for the ward provides some insight into these findings (Figure 2B). Individuals 7108 and 7128 were never present on ward X, but were mutually in contact with 7074 throughout the duration of the outbreak via known household contacts. The health care worker 7129 was present on ward X at the same time as many of the other individuals, but became symptomatic at a later point; the later onset of symptoms suggests that 7129 was infected by another individual in the outbreak without passing the virus on within the ward. The overall picture we discover is what may be a single outbreak of linked cases on ward X, potentially started by a patient, but largely involving HCWs both on and off the ward.
Analysis of data from ward Y revealed a less complex chain of events (Figure 2C). Precisely two clusters of individuals were inferred from the complete dataset, with individuals 1773, 2914, and 4255 forming one mutually interconnected set of infections, and the individuals 4902, 4633, and 4493 forming a second. While location data was missing for the latter three individuals the mutual connections between individuals are again understandable from the location data that do exist (Figure 2D). We note that in ward Y, cases were spread over a longer period of time than in ward X. In this case, we find two potential outbreaks between HCWs on the ward, with other cases reported on the ward not being linked to these individuals. Our results match the nature of the two wards as ‘green’ and ‘red’. Where ward X was designated for patients who were in theory free from COVID-19 infection, a coherent cluster of infection, potentially indicating a single introduction of the virus into the ward, was responsible for all of the observed cases. By contrast, the nature of ward Y as a designated COVID-19 ward led to multiple introductions of the virus onto the ward, perhaps two of those cases leading to ongoing nosocomial transmission.
In order to assess the value of location data we repeated our estimation in their absence, using only viral genome sequence data and the dates on which individuals first reported symptoms. Location data generally reduces the inferred potential for viral transmission; under the logic of our method, individuals who are not in the same place at the same time cannot infect one another. The value of location data in increasing the precision with which networks of links between cases of infection is shown by the results from ward X (Figure 3A). While the overall pattern of data shows general connections between individuals, the independence of the transmissions between 7108, 7128, and 7074 from the remainder of the network was lost in the absence of spatial data. Spatial data in our model was defined in terms of presence or absence on a ward, more refined information not being available. An analysis of data from ward Y showed an intriguing result, with previously unseen potential links between individual 2019 and the first cluster, and between 3327 and the second cluster (Figure 3B). These HCW displayed symptoms earlier than the people in their respective clusters, consistent with being the original cases in each case. Further, phylogenetic reconstruction showed that the sequences from these individuals were consistent with their being linked (Figure 3C; similar data for ward X is shown in Supporting Figure 3). However, the location data do not show them as working shifts on ward Y at the same time as any of the other linked individuals were present. We suggest that unrecorded contacts may exist in this case.
A. Output from the a2bcovid package given data from ward X, omitting location data for individuals. The plot shows potential links between infections. Identifiers of individuals are coloured in either black (patients) or red (HCWs). Squares in the grid indicate that transmission from one individual to another is consistent with our model (red), borderline (yellow) or unlikely (blue). B. Output from the a2bcovid package given data from ward Y, omitting location data for individuals. C. Phylogenetic relationship between sequences collected from individuals on ward Y. The tree was constructed manually using a principle of maximum parsimony[38]. Red digits indicate the number of substitutions between sequences from each individual.
The potential for missing location data to prevent the identification of linked individuals shows that measuring location can be difficult, more so for HCWs than patients. While patients are unlikely to be highly mobile, HCWs move around the hospital outside of their shifts. Unless explicitly recorded, off-ward contacts between HCWs are unlikely to be noted, leading to the potential non-inference of genuine links. While missing location data cannot be unambiguously diagnosed as the cause of our result, this case highlights the limitations intrinsic to our approach. Our software may provide valuable insights, but does not replace the need for full epidemiological investigation.
Discussion
We have here set out a method for evaluating the likelihood of transmission between two individual patients, based upon the dynamics of SARS-CoV-2 infection, data describing times of co-location between individuals, and genome sequence data collected during infection. Applied in a pairwise manner to data from multiple cases of infection, it can identify potential cases of transmission among individuals who may or may not be epidemiologically linked. In a first application of our method, we analysed data from two hospital wards. In each, we identified cases where the data were consistent with viral transmission occurring between either patients or HCWs on the ward. Our method builds upon information that can be obtained from a phylogenetic analysis, incorporating data from multiple sources to present an easily-interpretable map of potential linked cases of infection. It is likely to be valuable in the initial assessment of potential cases of nosocomial transmission, highlighting pairs or clusters of individuals for further epidemiological assessment, and allowing for a more strategic deployment of resources for outbreak investigation and targeted interventions.
Our method brings together a variety of data, combining an evolutionary model for the analysis of sequence data with location information and details of the dynamics of viral infection. In contrast to standard phylogenetic approaches to sequence data, our model explicitly accounts for noise in the generation of a viral consensus sequence; using within-host data we identified a magnitude of error of a fraction of one nucleotide per genome. In rapidly evolving viruses for which transmissions are separated by longer periods of time, the within-host evolution of viral populations is likely to overwhelm the effect of noise in the sequencing process. However, for cases of acute infection, separated by only a few days, the extent of noise may be close to the expected evolutionary change in the population, making it an important factor to consider.
One limitation of our method is that it deals with consensus viral sequences rather than deep sequence data. Where available, detailed measurements of within-host viral diversity may lead to an improved picture of relationships between cases of viral infection. We note further that our tool analyses data in a pairwise manner; while distinguishing plausible from implausible links between cases of infection, it does not attempt to infer a complete reconstruction of a transmission network. Unobserved cases of infection are not considered. Our model used parameters which in some cases have been derived from early studies into SARS-CoV-2 spread. To account for the event that further research leads to a better understanding of viral transmission we provide options to perform calculations with user-specified parameters. We finally note that a statistical inference from our model does not guarantee the occurrence or non-occurrence of a specific transmission event. Our model is intended as a first step towards further epidemiological investigation.
We believe that the key application of our method will be in investigating nosocomial transmission of SARS-CoV-2. Within a hospital, potential cases of transmission may be obscured by a large number of cases of community-acquired infection. In a busy clinical setting, our tool has the ability to rapidly separate potentially linked cases from those which are likely to be unlinked. In this way we allow investigative efforts and epidemiological followup to be focused more precisely, concentrating effort on cases where transmission is a real possibility.
Methods
Model overview
An overview of the notation used in the description of our model is shown in Figure 4. For each individual (here termed 1 and 2) we collect dates when the person became symptomatic, (e.g. time S1 in the figure) Sequence data was collected after the onset of infection (e.g. time D1). Transmission between the two individuals is denoted as happening at the time T12. The likelihood of transmission is mediated by the locations of the individuals 1 and 2, the weight w12(t) describing the probability of physical contact between the individuals on day t.
An overview of our model for transmission events is shown in Figure 3. We divide time into discrete days. For each individual i, we denote by Si the date at which that individual became symptomatic, and by Di the date at which a sample of viruses were collected for genome sequencing. For each pair of individuals i and j we denote by wij(t) the probability that i and j were co-located on day t. Using these statistics, in combination with viral sequence data, we estimate an intrinsic likelihood that i infected j on any given day Tij. The likelihood that i infected j is then calculated by combining these values over Tij.
Quality control of sequence data
Sequence data was subjected to two levels of quality control. The first considered the coverage of the genome; a cutoff was applied in which sequences had to unambiguously describe nucleotides at 80% or more of the sites in the genome. The second considered ambiguous sites at variant positions in the genome. Comparisons between sequences were based upon differences at variant sites, at which different nucleotides were reported for different sequences in the set. Having identified variant sites, we considered the number of ambiguous nucleotides in each sequence at these sites; sequences with more than one ambiguous nucleotide at a variant site were excluded.
In some cases, multiple viral samples were collected from an individual. In such a case, we identified the earliest sequence with sufficient coverage of the viral genome, referring to this as the primary viral genome for the individual.
Remaining samples were used to improve the quality of the primary genome. On the basis that the probability of a substitution at a single site in the genome is very low, where the primary genome had an ambiguous nucleotide at a given site, and another sequence from the same individual reported a nucleotide at this site, this information was used to repair the primary viral genome. Where multiple sequences were collected, earlier sequences were preferentially used in this repair process.
Spatial data
Where available, data describing the location of individuals was stored as a weighted list of places and locations on which an individual was present in that location. With a hospital setting in mind, location data were treated at a resolution of 1 day, representing the presence or absence of individuals on a ward.
Weights were assigned to presence and absence statistics to allow a nominal model of uncertainty in the location of healthcare workers. Individuals were designated as being present on ward W with weight 1 if they were recorded as being in that location on that day. Reflecting the increased mobility of healthcare workers, night shifts which span more than one day, and uncertainties such as the potential for fomite transmission, health care workers were denoted as present on ward W with weight 0.5 on day t if they were on ward W with weight 1 on either of the days t-1 or t+1.
A contact metric describing the potential interaction between individuals was now defined as
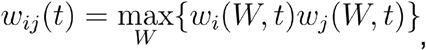where wi(W,t) is the weighted presence of individual i on ward W on day t.
Where location data was not available estimates were made of the values wi. Firstly, a location was inferred for these individuals. In the event that location data was available for some individuals, the most common ward W* in which these individuals were located was identified; individuals with no location data were assumed to be based in this ward. In the event that no location data were available, an arbitrary ward W*=WARD_01 was named. Next, taking into account the nature of a hospital outbreak, individuals were split into patients health care workers. Patients for whom location data was missing were assigned to be present on ward W* with probability 1 on every day of the time period in question. Reflecting shift patterns, health care workers were assigned to be present on ward W* with probability 4/7 on each day.
Missing symptom onset times
In some cases, the date at which an individual became symptomatic was unknown, either because the information is missing, or because individuals tested positive without experiencing symptoms. We imputed the date of symptom onset in both cases. To do so, we fitted distributions to data from 86 health care workers and 393 patients from Cambridge University Hospitals describing the dates at which symptoms were first reported and the dates at which individuals tested positive. A comparison of distributions between the two sources showed that a single shifted Gamma distribution best fitted the data (Supporting Figure 4, Supporting Table S2). Where data were missing the mean of this distribution was used to impute symptom onset dates from positive test dates.
Estimating noise in genome sequence data
In order to estimate the extent of measurement error in a consensus viral genome, we examined cases among data collected at Cambridge University Hospitals (CUH) for which more than one viral sample was sequenced. We identified 136 such patients, with between 2 and 9 samples collected from each individual and 336 samples in total. Each sample gave rise to a consensus sequence; we filtered the data to remove sequences with less than 90% coverage of the genome. For each pair of samples i and j, we recorded Hij, the Hamming distance between them, ΔTij, the absolute difference in time between the dates on which the samples were collected, measured in days, and the viral load of each sample, denoted by the CT scores Ci and Cj.
Following in principle a previous approach to estimating noise and rates of evolution [32], we then fitted a Poisson model to the data, deriving for each pair the likelihood component
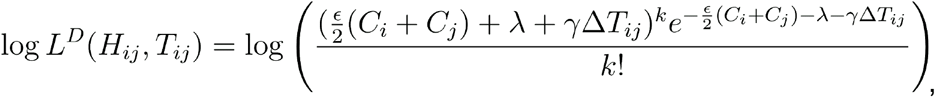and estimating the parameters ε, λ and γ so as to minimise the sum of the log likelihoods across all of the pairwise distances; we inferred the parameters 
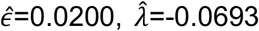and 
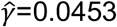. Here the function 
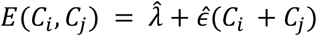provides a very simple estimate of the extent of measurement error in a distance measurement, expressed in terms of the CT scores of the two samples. For the purposes of our model this function was evaluated at the mean CT score of 24.091. This provided an estimate for the pairwise difference arising through measurement error, Ê, of 0.414 nucleotides, equivalent to 0.207 nucleotide errors per genome sequence. The estimate 
describes the mean rate of within-host evolution calculated across the within-host sample. It is expressed as a number of substitutions per genome per day, and is equivalent to a rate of 6.0 x 10−4 substitutions per locus per year, close to the value of 8 x 10−4 that has been calculated from global sequence data [33]. In so far as we require an estimated rate of evolution spanning both within-host and between-host evolution, we used in our model a rate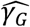 
of 0.0655 nucleotides per day, equivalent to this latter, globally estimated, rate of evolution.
To examine the effect of CT score affected our inference, a repeat calculation was performed in which viral load measurements was ignored; this gave a worse fit to the data under the Bayesian Information Criterion [34] (Supporting Table S1).
Likelihood of a transmission event
Our method used published likelihoods for the the infectivity profile of SARS-CoV-2 (in Figure 4 the length of the interval T12-S1), described as a gamma distribution, and of the time between an individual being infected and developing symptoms (in Figure 4 the length of the interval S2-T12), described as a lognormal distribution [16,17,35]. For arbitrary individuals i and j, these provide a likelihood of transmission having occurred between the individuals i and j on day Tij
We here define t= Sj - Si, and τ = Tij - Si. Reflecting the discrete nature of the data, each integral is calculated over a window of plus or minus half a day from the day in question. From the publications cited above, we have the estimated parameters α=97.1875, β=0.2689, s=25.625, μ=1.434, and σ=0.6612.
We combined this expression with a likelihood for the numbers of observed differences between the viral sequences observed from each patient. We began with the calculation of a consensus sequence from a set of locally acquired viral sequences; in our study we utilised a set of 1741 SARS-CoV-2 sequences collected by CUH; we refer to this as the CUH consensus. Next, given a pair of sequences, we calculated a pairwise consensus, defined as the nucleotide shared by the two sequences where the sequences agreed, and the nucleotide in the CUH consensus where the sequences differed. In evaluating a potential transmission event between the individual i and j we calculated the values Hi and Hj, the Hamming distances between the individual viral sequences and the pairwise consensus. We operate under an infinite sites assumption; that is, any given mutation can only be obtained once, while the reversion of mutations to the consensus effectively never happens.
We now note, in the notation of Figure 4, that if D1 is before T12, any variants observed in sequence data from individual 1 but not that from individual 2 can only arise from error. Under our assumption, such variants cannot revert in the time between D1 and D2 so must be caused by error in the observation. However, if D1 is after T12, such variants have the potential to evolve in the time between D1 and T12, in addition to being potentially caused by measurement error. We model the occurrence of such variants as arising through a Poisson model with rate equal to the error in a single sequence, plus the rate of evolution multiplied by the time in days after the day of transmission T12.
Considering variants observed in data from individual 2 but not from individual 1, these again can arise from error, or as a result of evolution going back either to the time of transmission T12, or to the previous time of sequencing D1, whichever is earlier. We again model the occurrence of such variants using a Poisson model. Combining the two Poisson distributions and considering the arbitrary individuals i and j we obtain the likelihood
where Pi = max{0, Di - Tij} and Qi = min{Di, Tij}.
Combining data from viral dynamics and genome sequence data we thus obtain an expression for the log likelihood that individual i infected individual j at time Tij.
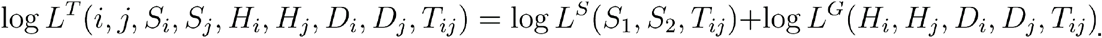Finally, assuming that the chance of transmission between any two individuals is small at any given time, we then calculate the log likelihood that i infected j by simple summation.
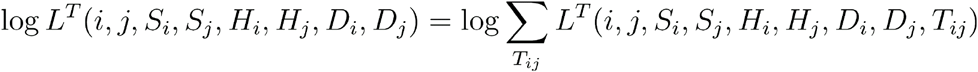Our method uses different sources of data. As a minimal input, our code calculates likelihoods based only upon dates of becoming symptomatic using the likelihood log LS. Adding in genome sequence data facilitates a more detailed calculation, involving log LG. Further data describing the locations of patients and health care workers refine the calculation, altering the likelihood LG according to the known locations of individuals, expressed through the values wij. While more data makes for a better inference, our method allows calculations to be performed even if an incomplete set of data is acquired.
Characterising the space of possible transmission events
Our method provides an interpretation of the raw likelihood values in terms of a measure of consistency with the underlying model of transmission, deeming each potential event as ‘consistent’ with our model, ‘borderline’, or ‘unlikely’. These descriptions were assigned on the basis of likelihood thresholds.
Likelihood thresholds were calculated based on a principle of hypothesis testing. Our likelihood function is based upon discrete input values; by calculating the value of the function across all plausible values, we identified a region of the input space containing 95% or 99% of the total likelihood. Having defined such a space we identified threshold likelihood values that are crossed going into or out of these regions. We then compared likelihoods generated from the data to these thresholds. This approach is analogous to calculating whether or not we would reject the null hypothesis that a point was emitted from our distribution of transmission events with p-value 0.05 or 0.01.
For the case in which sequence data were excluded from the calculation, we calculated the likelihood LS for all S2 ∈ [S1-11, S1+87]. For the case in which sequence data were included in the calculation we calculated the LT for all S2 ∈ [S1-11, S1+87], for all D1 ∈ [S1-5, S1+20], all D2 ∈ [S2-5, S2+20], and for all values H1 and H2 with H1+H2 ∈ [0, 10] and H1 ∈ [0, H1+H2]; these ranges were chosen according to values which provide a likelihood of at least 10−6 from each component of the distribution. Time-dependent likelihoods in each case were calculated for values of T12 ∈ [S1-11, S1+16], being summed to calculate likelihood spaces for LS and LT; both individuals were assumed to be present for the entire time of potential contact. The resulting likelihoods were then sorted; we denote these Li so that for any i<j, Li ≥ Lj. We then calculated threshold values T95, and T99, converting our likelihoods into nominal p-values. Here T95 is the maximum value of log LI for which
where the second sum was calculated over all Li and each sum was calculated over raw (not log) likelihood values. Similarly, T99 was defined as the maximum value of log LI for which
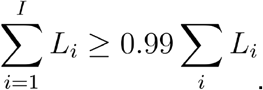These thresholds represent conservative estimates of the likelihoods that 95% and 99% of genuine transmission events will achieve; if our likelihood function was used to generate simulations of transmission, 95% of generated events would correspond to a likelihood greater than T95. The conservative nature of the estimates arises from the assumption of the individuals being in constant contact; likelihoods from events involving partial contacts are more likely to be lower than the threshold values.
While no set of input data can prove incontrovertible proof that a transmission genuinely occurred between two individuals, our comparison of likelihoods from the model to threshold values gives rise to a rapid, quantitatively-based assessment of whether input data are consistent with transmission having occurred. Plots showing aspects of the likelihood surface are shown in Supporting Figure 5.
Study setting, participants and data collection
This study was conducted at Cambridge University Hospitals NHS Foundation Trust (CUH), a secondary and tertiary referral centre in the East of England. SARS-CoV-2 positive cases tested at the on-site Public Health England (PHE) Clinical Microbiology and Public Health Laboratory (CMPHL) were identified prospectively from 26th February to 17th June 2020. The CMPHL tests SARS-CoV-2 samples submitted from over thirty organisations across the East of England (EoE) region and all samples from CUH. The majority of samples were tested using an in-house validated qRT-PCR assay targeting the SARS-CoV-2 RdRp genes, as described in a previous publication [5], with more recent samples tested using the Hologic Panther™ platform [36]. Patient metadata were accessed via the electronic healthcare record system (Epic Systems, Verona, WI, USA). Metadata collected included patient demographic information, duration of symptoms, sample collection date and location (ward and hospital). Patients and samples were assigned unique anonymised study codes. Metadata manipulations were performed using the R programming language and the tidyverse packages installed on CUH Trust computers.
Sample sequencing
All samples collected at CUH and a randomised selection of samples from the EoE region were selected for nanopore sequencing on-site in the Division of Virology, Department of Pathology, University of Cambridge. This enabled us to rapidly investigate suspected hospital acquired infections at CUH as previously described [5]. Briefly, a multiplex PCR based approach was used according to the modified ARTIC version 2 protocol with version 3 primer set, and amplicon libraries sequenced using MinION flow cells version 9.4.1 (Oxford Nanopore Technologies, Oxford, UK). Sequences were made publicly available as part of COG-UK (https://www.cogconsortium.uk/) via weekly uploads with linked metadata onto the MRC-CLIMB server (https://www.climb.ac.uk/).
Samples collected via the CUH healthcare worker (HCW) screening programme were also prioritised for on-site nanopore sequencing, as previously described [37]. This programme entailed asymptomatic screening of selected wards, symptomatic testing of self-presenting HCW and testing of symptomatic contacts of positive HCW. After a HCW tested positive, members of the HCW screening team contacted the HCW and retrospectively collected data on symptom onset date, symptomatology, household contacts, their job role, and which wards they had worked in for the preceding two weeks. Most positive HCW could identify symptoms on retrospective questioning, even if they were identified in the asymptomatic screening arm; however, a small minority were genuinely asymptomatic and never went on to develop symptoms. HCW presenting acutely to medical services at CUH were not part of the HCW screening programme, but were identified as HCW from their medical records as part of hospital surveillance.
Identifying hospital-associated outbreaks for investigation
Patients tested at CUH were categorised on the basis of time between admission and first positive swab into different groups reflecting the likelihood that their infection was community or hospital acquired, as previously described (Meredith et al, LID 2020). The categories used were: 1) Community onset, community associated (first positive sample <48 hours from admission and no healthcare contact in the preceding 14 days); 2) Community onset, suspected healthcare associated (first positive sample <48 hours from admission with healthcare contact in the preceding 14 days); 3) Hospital onset, indeterminate healthcare associated (first positive sample 48 hours to 7 days post admission); 4) Hospital onset, suspected healthcare associated (first positive sample 8 to 14 days post admission); 5) Hospital onset, healthcare associated (first positive sample >14 days post admission); 6) HCW.
All CUH patients in categories 3, 4, and 5 (hospital onset with indeterminate, suspected or definite healthcare associated COVID-19 infections) and 6 (HCW) were included for analysis and integrated into the HCW screening dataset of positive HCW. The main wards the HCW had worked in prior to testing positive and the ward where each patient had first tested positive were used to identify ward clusters of hospital-associated infections. The ward clusters are named anonymously here as Wards X and Y.
Data Availability
Sequence data analysed were generated by previous research studies and are available from the GISAID server. A list of sequence IDs are provided in Supplementary Material. Sequences and accompanying metadata has been uploaded onto the MRC-CLIMB server.
Availability of code
Our app is suitable for use with the R package and can be downloaded from http://github.com/chjackson/a2bcovid.
Acknowledgements
This work was funded by COG-UK, which is supported by funding from the Medical Research Council (MRC) part of UK Research & Innovation (UKRI), the National Institute of Health Research (NIHR) and Genome Research Limited, operating as the Wellcome Sanger Institute; We also acknowledge the support from the Wellcome (Senior Clinical Fellowship to MPW (ref: 108070/Z/15/Z), Senior Research Fellowship to SB (ref: 215515/Z/19/Z), Senior Fellowship to IG (ref: 097997/Z/11/Z); Collaborative Grant to CJH (ref: 204870/Z/16/Z); the Academy of Medical Sciences & the Health Foundation (Clinician Scientist Fellowship to MET), the NIHR Cambridge Biomedical Research Centre (to BW, MET) and the NIHR Clinical Research Network Greenshoots award (to EGK). CJRI was supported by Deutsche Forschungsgemeinschaft (DFG) Grant SFB 1310. We acknowledge MRC funding (ref: MC_UU_00002/11).
