Risk factors for mortality among hospitalized patients with COVID-19

Data Source

The Optum® de-identified COVID-19 EHR dataset was used to identify patients hospitalized with COVID-19. The dataset consists of a national sample of inpatient and outpatient medical records sourced from hospital networks from across the U.S. Data are de-identified in compliance with the HIPAA Expert Method and managed according to Optum customer data use agreements [4]. Inpatient mortality was captured in the dataset as month of death. Age for those 89 and older was aggregated in the dataset.

Study Cohort

To be eligible for the hospitalized cohort in this study, patients were required to be older than 18 years old and have: (1) a U07.1 or U07.2 diagnosis, (2) a positive SARS-CoV-2 diagnostic test (e.g., either molecular or antigen tests) or (3) a B97.29 diagnosis with the absence of a negative SARS-CoV-2 molecular test within a 14-day window. Eligible hospitalizations required inpatient or emergency room overnight visits with a COVID-19 diagnosis or starting up to 21 days after a COVID-19 diagnosis. Contiguous ER and inpatient visits, with up to a 1-day gap were considered a single hospitalization. The date of admission was used as index date when COVID-19 diagnosis occurred before hospitalization, otherwise index date was set to the date of COVID-19 diagnosis. Only the first hospitalization was considered in this study. The study period was February 20, 2020 to June 5, 2020.

Outcome

The outcome was a binary measure of in-hospital all-cause mortality. To ensure that there was sufficient follow-up time, patients were removed from the sample if their index date was less than 2 weeks prior to the date the Optum dataset was censored (June 5), resulting in the removal of approximately 5% of the overall study population. Evidence from the U.S. Centers for Disease Control on time to death following hospital admission (median: 5 days, interquartile-range: 3-8 days) [12] suggests that this was sufficient to capture most deaths.

Predictors

Candidate predictors were chosen based on prior research and/or clinical consultation [5]. They included demographics, comorbidities, vital signs, laboratory results and calendar time.

Demographic variables were age, sex, race, ethnicity, geographic division, and smoking status. Comorbidities were identified based on ICD-9 and ICD-10 codes within a year of index date and included hypertension, diabetes, and those included in the Charlson Comorbidity Index (CCI).

Vital signs considered were peripheral oxygen saturation, systolic blood pressure, heart rate, respiratory rate, temperature, and body mass index (BMI). Laboratory results for aspartate aminotransferase (AST), C-reactive protein (CRP), creatinine, ferritin, lactate dehydrogenase (LDH), troponin I, lymphocyte count, neutrophil count, platelet count (PLT), and white blood cell count (WBC) were obtained. D-dimer and procalcitonin laboratory measures were also considered but were dropped due to very high missingness (90% and 49%, respectively). We restricted vital signs and laboratory results to those within a [-3,+1] day window surrounding the index date and used the (median of the) value(s) closest to the index date when multiple values were available within the window.

To capture trends over time, we also derived a calendar time variable measured as the number of days between a patient’s index date and the date of the first case in the data.

Missing data for each of the candidate predictors is summarized in Supplement Section 3.2. There was significant missing data for race, ethnicity, BMI, smoking status, and some of the vital signs and laboratory results. Multiple imputation was consequently used as described below.

Model Development and Statistical Analysis

A multivariable logistic regression was used to model mortality. To protect against overfitting, we first performed variable selection by fitting a logistic model with a group lasso penalty [13,14]. We repeatedly fit the lasso model 100 times and used 10-fold cross-validation during each of the 100 iterations to select the optimal tuning parameter, “lambda.” Variables with non-zero coefficients in at least 90 percent of the iterations were included. In practice, only three variables were excluded: rheumatoid disease, peptic ulcer disease, and neutrophil count (Supplement Section 5).

The model with all predictors chosen by group lasso was the “full” model. For comparison, we fit 4 more parsimonious models with the following predictors: (i) age only, (ii) comorbidities only, (iii) all demographics (and calendar time), and (iv) demographics (and calendar time) and comorbidities. Non-linear relationships between mortality and continuous covariates were modeled using restricted cubic splines. 3 knots were deemed sufficient based on graphical assessment of univariate fits in nearly all cases; 4 knots were used for respiration rate to capture a bathtub-shaped relationship with mortality. These graphical assessments also showed that a few outliers were influencing the fit of some of the laboratory results. They were consequently truncated from above (at the “outer fence” defined as the third quartile plus three times the interquartile range), which led to stronger and more clinically meaningful relationships (Supplement Section 3.5).

Predictor effects were summarized in four ways. First, coefficient estimates were translated into clinically meaningful odds ratios. Odds ratios for each value of a categorical variable were computed based on comparisons to a reference group. Odds ratios for continuous covariates were based on changes in value from the 25th percentile to the 75th percentile. Second, we predicted log odds across different values of each predictor and visually assessed the effects. Third, predicted probabilities were computed by age, sex, and calendar time for a random sample of 1,000 patients and then averaged across patients. Fourth, variable importance was assessed using □2 minus degrees of freedom from a Wald test that tests the hypothesis that the coefficient of each term associated with a variable (e.g., all categories of a categorical variable or all spline terms of a continuous variable) is zero [15,16].

To validate the model, we randomly split the data into a training and test set using an 80/20 split and evaluated the model in both the training and the test sets. Model performance was assessed using the C-index (AUROC) and Brier score. To assess overfitting, 50 bootstrap replications were used to quantify “optimism” in the training set, defined as the average of differences in model performance between the training and bootstrapped samples. Calibration was assessed using a calibration curve that compared predicted probabilities with actual probabilities.

Missing data was imputed using multivariate imputation by chained equations (MICE) [18]. A total of 5 datasets were imputed. Assessment of the imputation was performed by comparing the distribution of the missing imputed data to the observed data for each predictor. Supplement Section 4.3 shows that these distributions were very similar for each variable, which suggests that the imputation was adequate. Coefficient estimates and confidence intervals were combined across the imputations using Rubin’s rule [17].

Analyses were performed using R 4.0.0. We used three main R packages in the analysis: mice for multiple imputation, oem to fit the group lasso, and rms to fit the multivariable logistic regressions, summarize the coefficients, and validate the model [14,15,18]. Additional details of the methodology are available in the Supplement.

Characteristics of the Study Population

We identified 17,086 patients that met the inclusion criteria for the COVID-19 hospitalized cohort. The characteristics of the 13,658 patients included in the training set are described in Table 1 and in additional detail in Supplement Section 3.

The median age was 62 years old (Interquartile range [IQR]: 49, 75). The cohort was composed mostly of male (51.9%) non-Hispanic whites (56.0%). Most patients resided in the Middle Atlantic (34.9%) and East North Central (34.9%) geographic divisions, which mirrors the initial surge of cases in the U.S. Patients had high rates of comorbidities: 58.6% had hypertension, 33.8% had diabetes, 26.6% had chronic pulmonary disease (CPD), 20.7% had renal disease, and the median CCI score was 1 (IQR: 0, 3). The majority of patients were overweight (30%) or obese (48%). Median oxygen saturation was 96.0%, and 25% of patients had oxygen saturation lower than 94.0%. The median temperature was 37.0 C (IQR: 36.7, 37.4). Patients had a median ferritin of 510.0 ng/ml (IQR: 224.0, 1080.0) and median CRP of 79.1 mg/l (IQR: 34.0, 140.0). Among the 9.6% of patients with results available for fibrin d-dimer, the median result was 750 ng/ml (IQR: 390.0, 1540.8).

Compared to survivors, non-survivors were more likely to be male (57.1% vs. 51.0%) and older (median 77 years old vs. 59 years old). Non-survivors also had more comorbidities (median CCI of 3 [IQR: 1,5] vs. 1 [IQR: 0, 2]) including dementia (25.0% vs. 7.4%), renal disease (39.3% vs 17.3%), diabetes (43.6% vs 31.9%), and hypertension (77.2% vs. 55.1%). Similar trends were observed for laboratory findings and vitals: non-survivors had higher heart rates (median beats/min of 89.0 vs. 87.0) and respiratory rates (median breaths/min of 22.0 vs. 19.5), and lower oxygen saturation (median 95.0% vs. 96.0%). However, no substantial difference was observed in temperature (median 37.1 C vs 37.0 C) or in BMI (median 28.1 vs. 30.0). Non-survivors had higher CRP (median mg/L of 116.0 vs 72.2), ferritin (median ng/mL 747.5 vs. 470.0), and fibrin d-dimer (median ng/mL of 1,345 vs 692.5).

A comparison of the training and test sets is provided in Supplement Section 8.1. There were no meaningful differences in demographics, comorbidities, vitals or laboratory results.

Predictor Effects

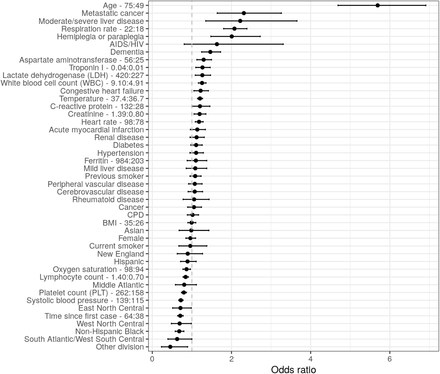
Odds ratios from the multivariable logistic regression are displayed in Figure 1. Age was a very important predictor as the odds of death for a 75 year old (75th percentile) were around 6 times than for a 49 year old (25th percentile). Metastatic cancer, moderate/severe liver disease, hemiplegia/paraplegia, and dementia were also highly positively associated with mortality and precisely estimated. Mortality decreased over time as evidenced by the negative odds ratio for calendar time. Other important predictors were vital signs and laboratory results. Lower values of PLT and higher values of AST, troponin I, CRP, WBC, LDH, and creatinine were associated with increased mortality. Similarly, abnormally low levels of oxygen saturation were associated with higher mortality as were abnormally high values of respiration rate, heart rate, temperature, and BMI. Since some of the predictor effects were non-linear, plots showing the non-linear predicted effects of the continuous variables on the log odds scale are displayed in the Supplement Section 6.6. The log-odds plot shows, for instance, that mortality is higher at both lower and higher levels of temperature and systolic blood pressure, and that the strong negative relationship between oxygen saturation and mortality is only present below around 95%.

• Download figure
• Open in new tab

Figure 1:

Odds ratios of mortality from the full multivariable logistic regression. Error bars represent 95% confidence levels. Interquartile-range odds ratios are used for continuous predictors (upper quartile: lower quartile). Reference groups for categorical predictors are as follows: race/ethnicity = “non-Hispanic white”, division = “Pacific”, sex = “Male”, smoking = “Never smoker”.

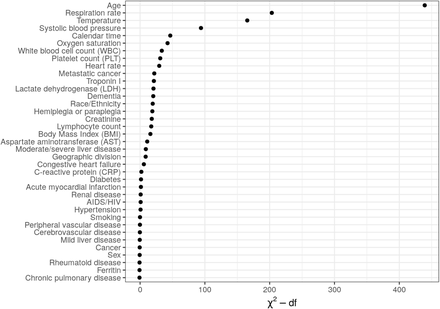
One limitation of the odds ratio is that it can be difficult to compare the relative importance of categorical and continuous variables or transformed continuous variables. Figure 2 consequently displays the importance of each variable based on Wald tests. Age is the most important predictor by a considerable amount. Laboratory results and vitals tend to be more important predictors than either comorbidities or demographics: impactful predictors include respiration rate, temperature, oxygen saturation, heart rate, WBC, and LDH. Calendar time is also an important predictor.

• Download figure
• Open in new tab

Figure 2:

Ranking of importance of predictors of mortality from the full multivariable logistic regression. A higher value of “Chi-squared minus degrees of freedom” implies that a predictor has a larger contribution to the fit of the model.

One potential concern with these results is that laboratory results and vitals might be mediators that are correlated with demographics and comorbidities (Supplement Section 3.4.4). We assessed this in Supplement Section 6.5 by removing labs and vitals from the model. The odds ratios tended to be fairly stable. Female sex was a notable exception as the odds ratio changed from approximately 0.7 to almost 1.

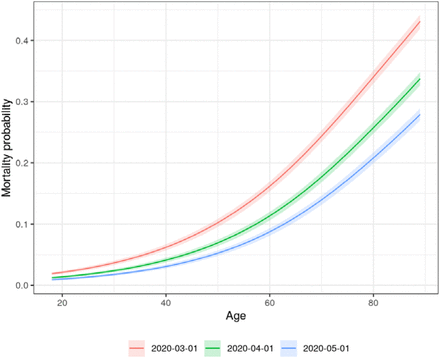
To assess the clinical impact of changes in predictors, it is helpful to assess predicted probabilities of mortality. These are displayed across levels of age and calendar time for a random sample of 1,000 patients in Figure 3. The effect of age on the probability scale is exponential and increasingly sharply at older ages. In March of 2020, a hospitalized 80-year-old had a predicted probability of death of 34% whereas a 70-year-old had a predicted probability of death around 10 percentage points lower. The predicted probability of death for an 18-year-old at the same date was less than 2%. Mortality probabilities did decrease considerably over time with mortality rates for 80-year-olds approaching 20% by May 2020.

• Download figure
• Open in new tab

Figure 3:

Predicted probability of mortality from the full multivariable logistic regression by age and calendar time. Each curve represents a specific hypothetical index date. Age and calendar time effects are adjusted for all variables in the full model. Predictions for each age and calendar time combination are averaged over a random sample of 1000 patients.

Validation and Predictive Performance

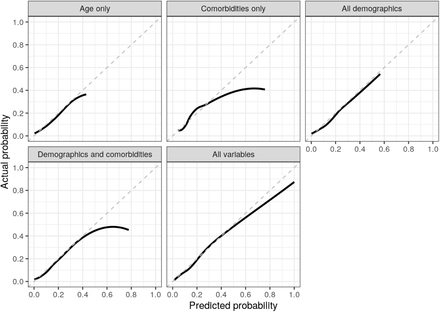
Calibration curves comparing predictive probabilities to actual probabilities among patients in the training and test sets are shown in Supplement Section 7.2 and Figure 4, respectively. In the training set, the bias-adjusted and unadjusted curves were similar, and “optimism” was approximately zero, suggesting that there was little overfitting; however, there was more overprediction for higher risk patients in the test set. In both cases, models including comorbidities tended to be poorly calibrated for more at risk patients, while the full model was better calibrated.

• Download figure
• Open in new tab

Figure 4:

Calibration curves from predictions of the logistic regression model on the test set by model specification. Points on the dashed 45-degree line imply that the predicted probability is equal to the actual probability.

Higher predicted probabilities of mortality were much more common in the full model than in any of the other models. In other words, the variance of the predictions was higher implying that the full model was better able to discriminate between patients. This was also reflected in Table 2, which reported estimates of the C-index and Brier score. In the test set, the C-index improved from 0.756 in the age only model to 0.874 in the full model and the Brier score decreased from 0.111 to 0.087. Results were similar in the training set. Notably, there was no appreciable difference in either the Brier score or the C-index between the age only model, the demographics model, or the demographics and comorbidities model.

Comparison with Other Studies

A living systematic review of existing prognostic models has been conducted by Wynants et al. [5] and 50 prognostic models have been identified to date. A subset of those predict mortality among hospitalized patients.

Most prognostic models are based on data from China [19-24], although others have been developed with data from the United Kingdom [25,26], Mexico [27], South Korea [28], Israel [29], the U.S. [30-32]), and a mix of countries [33]. Our study differs from the other U.S. studies in that it includes a broader cohort of patients encompassing all geographic regions.

Models have typically been trained on smaller datasets, with most consisting of <1,000 and a few ranging from 1000-3000 [28,30,31]. Only one study, to our knowledge, had a sample size larger than 10,000 patients and was based in Mexico [27]. Smaller sample sizes not only increase the likelihood of overfitting, but also reduce the ability to detect important risk factors.

One advantage of our approach compared to more “black box” prediction models, is that the effects of the covariates were interpretable [34,35]. For instance, we used splines [17,18,36] to show that the probability of death increases exponentially with age. The strength of this relationship was consistent with other studies including Gupta et al. [26], who evaluated the performance of models from 19 studies (14 of which were COVID-19 specific) on an independent dataset of 411 patients hospitalized for COVID-19 in the United Kingdom and found that no other variables added additional incremental value beyond age. Age may be a strong predictor because while it is correlated with the comorbidities specified in the model, it also likely captures other unspecified comorbidities that may be associated with worse outcomes. Additionally, age may be associated with altered immune function that could result in slower viral clearance, or a hyperactive immune response that could contribute to severe clinical manifestations of the disease [37].

Our results also differ from Gupta et al. [26] in that laboratory results and vital signs added non-negligible incremental value to the discriminative ability of our predictions. Oxygen saturation, temperature, and respiration rate were among the most important risk factors in the model, which is consistent with other models of mortality, both amongst patients with COVID-19 [22,25,38] and in more general populations [39-41]. The positive relationship between higher levels of BMI and mortality was consistent with prior research [42,43].

Troponin I, LDH, and PLT were among the most important laboratory results, which has been documented elsewhere [5,44,45]. Troponin and LDH elevations may reflect more severe microvascular dysfunction which could lead to myocardial and other end-organ injury. Lower PLT counts could reflect increased consumption due to macro- and micro-thromboses, which have been described clinically and in autopsy studies [46], and which may be associated with and exacerbate microvascular dysfunction. Of note, the lasso model selected WBC and lymphocyte count for inclusion and excluded neutrophil count. We explored this further by running a separate model omitting WBC and found that neutrophil count had similar variable importance to WBC in this specification. Neutrophil count also had a strong relationship with mortality in univariate fits (Supplement Section 3.5). Our results are therefore consistent with prior work showing that mortality is associated with lower lymphocyte and higher neutrophil counts [47,48]. We did not find an association between ferritin and mortality despite studies showing that severe illness is characterized by hyperferritinemia [49].

Finally, while comorbidities added little prognostic information beyond age, it is important to distinguish these findings from those based on a general population diagnosed with COVID-19 since risk factors that are predictive of hospitalization (or death in the general population) may not be predictive of mortality conditional on hospitalization. Petrilli et al. [44] provides some evidence consistent with this in that comorbidities were more important predictors of hospital admission than of severe illness and mortality among hospitalized patients. On the other hand, a number of studies have also found evidence that even in hospitalized populations, comorbidities such as hypertension, cardiovascular disease, CPD, and diabetes were predictive of severe illness or mortality [42,50-53]. However, even these findings are not necessarily inconsistent with our results since comorbidities and BMI tended to be “statistically significant” despite not meaningfully improving predictive performance. Furthermore, the wide range of mortality reported in case series of patients with severe COVID-19 may indicate that factors that predict severe disease do not necessarily predict mortality [54,55].

Study Limitations

This study is not without limitations. First, there was considerable missing data, especially for laboratory results. We attempted to overcome this limitation using multiple imputation, although the coefficient estimates are only guaranteed to be unbiased if the data are missing at random and the missing mechanism is known. While this is an untestable assumption, our diagnostics were not suggestive of problems in the imputation as the distribution of the observed and imputed data were very similar.

Second, many of the laboratory results contained outliers. Although we truncated these variables to improve fit, predictions for new patients with extreme laboratory values lying outside of the chosen bounds are inherently uncertain. The presence of outliers could also imply that some laboratory values have been miscoded. This miscoding is a form of measurement error that would attenuate the relationship between mortality and the laboratory values [56,57].

Third, we did not have data on the day of death or out-of-hospital mortality. The latter could mean that mortality is underestimated if patients are discharged from the hospital and later die at home from COVID-19. Evidence suggests that COVID-19 deaths in the hospital comprise 38% of all deaths, but since the proportion of those 38% who were previously hospitalized is unknown, it is difficult to calibrate the extent of this potential bias [12]. Without day of death data, we were unable to perform time to event analyses that allowed for right censoring, raising the possibility of further underestimation of mortality. While we did aim to mitigate this limitation by dropping all observations with index dates less than 2 weeks from the data release date and controlling for calendar time in our models, future work should consider time to event analyses if the data permits.