Abstract
Early CoVID-19 growth obeys: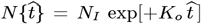 
, with Ko = [(ln 2)/(tdbl)], where tdbl is the pandemic growth doubling time. Given 
, the daily number of new CoVID-19 cases is 
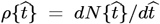. Implementing society-wide Social Distancing increases the tdbl doubling time, and a linear function of time for tdbl was used in our Initial Model:
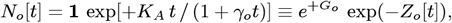to describe these changes, where the [t]-axis is time-shifted from the 
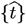–axis back to the pandemic start, and Go ≡ [KA/ γo]. While this No[t] successfully modeled the USA CoVID-19 progress from 3/2020 to 6/2020, this equation could not easily model some quickly decreasing ρ[t] cases (“fast pandemic shutoff “), indicating that a second process was involved. This situation was most evident in the initial CoVID-19 data from China, South Korea, and Italy. Modifying Zo[t] to allow exponential cutoffs:
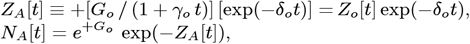resulted in an Enhanced Initial Model (EIM) that significantly improved data fits for these cases.
After 6/2020, many regions of the USA “opened up”, loosening their Social Distancing requirements, which led to a sudden USA CoVID-19 Resurgence. Extrapolating the USA No[t] 3/2020-6/2020 results to 9/2020 as an Initial Model Baseline (IMB), and subtracting this IMB from the newer USA data gives a Resurgence Only function, which is analyzed here. This USA CoVID-19 Resurgence function differs significantly from the No[t] IMB functional form, but it was well-modeled by the NA[t] fast pandemic shutoff function. These results indicate that: (a) the gradual increase in tdbl doubling time from society-wide shut-downs is likely due to eliminating of a large number of population gathering points that could have enabled CoVID-19 spread; and (b) having a non-zero δ o fast pandemic shutoff is likely due to more people wearing masks more often [with 12 Figures].
1 Introduction
The CoVID-19 pandemic started late in 2019, becoming world-wide in early 2020, with CoVID-19 spread evolving differently in various areas. Many publicly available databases were set up to track the disease, to assist epidemiologists, scientists, and policy makers in visualizing CoVID-19 spread. The widely available bing.com1 CoVID-19 database was used here. These databases under-pin model projections, allowing quick evaluation of how different inputs affect the predicted outcome. Our goal was to empirically model a wide range of data with a small number of parameters, where different values for these parameters could span the range of observed CoVID-19 evolution among regions.
The 
number of CoVID-19 cases starts with an exponential growth:
where NI at time 
is the number of infected people, Ko is a rate constant for how fast an infected person spreads CoVID-19 to others, and tdbl is the pandemic doubling time. This is the basis for a large number of SEIR (Susceptible, Exposed, Infected, and Recovered or Removed) pandemic models, which are often implemented as systems of local differential equations.
Implementing society-wide measures for non-infected people is inherently a non-local process. How it impacts pandemic spread is often not the main focus of SEIR models, which are local. However, when governments mandated Social Distancing, starting with shut-down of large-scale gathering places at some 
point, the 
response was fairly quick. Within days, the tdbl was empirically observed to gradually lengthen, likely due to these shut-downs preventing a large number of people from gathering together and spreading CoVID-19.
Our prior work2-3 showed that an Initial Model2, with a linear function of time for gradual tdbl changes:
successfully fit a lot of early CoVID-19 pandemic data. More importantly, Eq. [1.2b] showed that this Initial Model allows for CoVID-19 pandemic shut-off, prior to infecting the whole population.
An exception was CoVID-19 spread in Italy, having a much faster pandemic shut-off than Eq. [1.2a] predicted. We attributed this to a second CoVID-19 mitigation process that was modeled with a δo exponential decay time constant:
where δo = 0 is the absence of this second process. Including this second process4 gave an Enhanced Initial Model (EIM), which then successfully modeled CoVID-19 spread in Italy.
While the Initial Model2-3 successfully predicted the USA CoVID-19 evolution from March 2020 through early June 2020, widespread “opening-up” of various gathering places (such as local bars and hair and nail salons) in mid-June 2020 created a large-scale USA CoVID-19 Resurgence.
A new model for USA CoVID-19 Resurgence is developed here. Our prior (3/2020-6/2020) USA CoVID-19 function was used as an Initial Model Baseline (IMB). This IMB was projected out to 9/2020, and subtracted from all follow-on USA data, to give a Resurgence Only function. As detailed next, the number of USA CoVID-19 Resurgence cases can substantially exceed the expected pre-Resurgence total. More importantly, this CoVID-19 Resurgence was also found to require a δo ≠ 0 EIM in order to achieve a good data fit.
This δo ≠ 0 result is similar to the prior analysis of CoVID-19 spread in Italy4. The fact that the δo ≠ 0 EIM function is needed to model Resurgence, instead of an Eq. [1.2a] IMB -type function, helps to identify the CoVID-19 second process. After the Social Distancing period of 3/20-6/20, new post-6/20 society-wide recommendations or mandates to wear masks were put in place, which likely gives rise to this faster Resurgence pandemic shut-off.
2 Background
Let 
model the total number 
of CoVID-19 cases in a locality, with 
having end-points {NI, NF}. Then 
, and:
where 
is the predicted number of daily new CoVID-19 cases. Early CoVID-19 growth obeys 
, with Ko = [(ln 2)/tdbl], where tdbl is the pandemic doubling time, but if society-wide Social Distancing starts at 
, then tdbl can lengthen for 
. The prior 
exponential growth phase, before Social Distancing started, is not applicable for estimating Social Distancing parameters.
Our Initial Model for CoVID-19 spread and tdbl lengthening2-3 is given in the above Eqs. [1.2a]-[1.2b]. In Eq. [1.2a], different NI values alter the 
points. However, all these time axes can be shifted to a new t = 0 point that estimates the CoVID-19 pandemic start:
along with the boundary conditions that No[t = t I] NI and No[t = tF] ≈ NF occur over the (tF − tI) time interval. The tI value is set by the prior {Ko, αs} values. Specifically, at 
, Eq. [1.2b] must give:
which then individually sets {tI, tF} as follows:
with the {NI, t I, NF, t F} group uniquely determining 
:
which sets the Eq. [2.2b] Zo[t] function. The total number of cases 
at the pandemic end, and the long-time tail for αo[t] are each given by:
The {0 < t < tI} period, prior to Social Distancing start, estimates what the pandemic would have looked like, had Social Distancing begun at t = 0.
Using USA CoVID-19 data from bing.com1 from 3/21/2020 through 6/7/2020, we derived the following Initial Model Baseline (IMB) best fit as shown in Figs. 1-2, using these parameter values:
Predicted Number of Daily CoVID-19 Cases has a peak of 30,727 cases/day on 4/15; with 4,499,494 cases total; and ∼5,783 new cases/day at Day 200 on 9/27/2020.
Revised bing.com data, circa 5/3/2020, changed all values back to the pandemic start. Initial Model appears to be a good data fit.
Shortly after 6/7/2020, many states and cities around the USA “opened up” nearly simultaneously, loosening Social Distancing restrictions. This optimistic action led to a sudden USA CoVID-19 Resurgence.
3 Initial Model for CoVID-19 Resurgence
To model CoVID-19 Resurgence, the Figs. 1-2 IMB curve values were subtracted from the new USA data totals. When the total number of CoVID-19 Resurgence cases, 
, showed a trend above the IMB baseline, then 
could be used as the 
data end-points. Let 
model this CoVID-19 Resurgence data, so that 
. Then:
where 
is the predicted number of daily new CoVID-19 Resurgence cases. Early CoVID-19 Resurgence can obey 
, where 
and 
is the pandemic Resurgence doubling time. Using an Initial Resurgence Model (IRM) that parallels the prior section IMB gives:
The best 
are set by minimizing the rms error between the Eq. [3.2a] function and the measured CoVID-19 Resurgence data. In Eq. [3.2a], the 
data where 
, are not used to estimate the 
pandemic Resurgence parameters. As Eq. [3.2b] shows, this IRM allows pandemic shut-off before the CoVID-19 Resurgence infects the whole population. In Eq. [3.2a], different 
values alter the 
points, but all these time axes can be shifted to a new t′ = 0 point that estimates the CoVID-19 Resurgence start:
Since the 
data end points span a time interval of 
, the constraints 
and 
determines 
as follows. Using a method similar to Eq. [2.3] and Eqs. [2.4a]-[2.4b], the best fit 
values from Eq. [3.2a] set 
:
with the 
group uniquely determining 
:
which sets the Eq. [3.3b] 
function. The total number of cases 
at pandemic end, and the long-term tail for 
are each given by:
showing that 
. Either 
or 
can be used as the primary variables. The IRM analysis results for the USA CoVID-19 Resurgence are shown in Figs. 3-4, using the best-fit 
values. The prior 
period in Fig. 3 estimates what the pandemic would have looked like, if Resurgence Social Distancing had begun at t′ = 0. The best fit parameter values for Figs. 3-4 are:
The Fig. 1 IMB has data through 6/7/2020. It was extrapolated to 8/27/2020, then subtracted from The actual data to create Resurgence Only data, which was then fitted using the Initial Model.
Initial Model Baseline (IMB) was subtracted from actual data to set Resurgence Only Data. Resurgence Start Day #1 was set to 6/13/2020 with N=15,650 cases above IMB.
Unfortunately, Fig. 3 shows that the 
IRM data fit is not that good. The 
function has a long tail, which overestimates 
, as the maximum number of CoVID-19 Resurgence cases at the pandemic end.
4 Enhanced Model: USA CoVID-19 Resurgence
Since the observed 
Resurgence data decreases much quicker than the IRM prediction, the USA CoVID-19 Resurgence has a fast pandemic shutoff, which is similar to our prior study3-4 of Italy CoVID-19 data. That Italy data was most successfully modeled by introducing a second process having an exponential decay in time. Generalizing the IRM model of Eq. [3.3a] similarly gives this Enhanced Initial Model (EIM) for Resurgence, where 
in Eq. [4.1c] characterizes this second process:
The above Eqs. [4.1a]-[4.1e] have these limits:
For easier data fitting when δo ≠ 0, the Eq. [4.2b] condition that NA(t′ = 0) = 1 can be relaxed. Adjusting NA(t′ = 0) allows 
to be preserved. Then both 
can be treated as model inputs. The 
prefactor in Eq. [4.1a] can be modified to give:
so that 
can adjust NA(t′ = 0), while keeping the same t′ = 0 point:
Here 
is the total number of CoVID-19 Resurgence cases at the pandemic end for this EIM model. Given values for 
, Eq. [4.4b] uniquely sets 
via:
The NA(t′) of Eq. [4.3] then gives this ρA(t′):
for the daily number of new CoVID-19 cases, providing a self-consistent analytic function for ρA(t′), instead using ρ A(t′) ≈ Δ NA(t′) / ≈ Δt′ as a numerical approximation. For long times, Eq. [4.6] becomes:
which exhibits a nearly exponentially decaying tail. Minimizing the rms error using a Logarithmic Y-axis vs linear-time axis gives Figs. 5-6, with these best fit parameter values and results:
EIM best fit with NA[t] ∼ exp(-ZA[t]) using enhanced ZA[t] function with exponential decay term, which significantly improves fit. Best fit uses Logarithmic Y-axis: ln(NA[t]) vs time.
EIM best fit with NA[t] ∼ exp(-ZA[t]) using enhanced ZA[t] function with exponential decay term. Datafit minimizes rms error on Logarithmic Y-axis.
The Fig. 6 Logarithmic Y-axis data fit is quite good, as is Fig. 5 when compared to the IRM Fig. 3. The faster decaying Fig. 5 ρA(t′) tail gives a significantly lower prediction for the total number of Resurgence cases at the pandemic end. Finally, a similar data fit is shown in Figs. 7-8, except the rms error was minimized using a Linear Y-axis vs linear-time axis for the ρA(t′) Resurgence data. It has the following best fit parameters, which are similar to the above Eq. [4.8] table results:
EIM best fit with NA[t] ∼ exp(-ZA[t]) using enhanced ZA[t] function with exponential decay term. Bestfit minimizes error on Linear Y-axis vs time w/ Y= dNA[t]/dt = Daily # New CoVID-19 cases.
EIM best fit with NA[t] ∼ exp(-ZA[t]) using enhanced ZA[t] function with exponential decay term. Deviations on Logarithmic Y-axis due to minimizing error using Linear Y-axis as given in Fig. 7.
These values form our best estimate for USA CoVID-19 Resurgence. Combining these results with the pre-Resurgence data fit of Figs. 1-2, gives Figs. 9-10 for the full USA CoVID-19 evolution, covering the entire 3/21/2020-8/27/2020 time frame. This final data fit captures virtually all of the shape nuances in the actual data. The predicted final number of USA CoVID-19 Cases at the pandemic end, from Eq. [2.7] and Eq. [4.9] is:
For CoVID-19 in the USA, Fig. 11 plots the ratio of the total number of deaths versus total number of cases (% vs time), based on the bing.com database1, which gives ∼2 9325% = (169, 108) / (5, 766, 718), as of 8/27/2020. This value is similar to the IHME 8/27/2020 value5 of ∼3 1065%, which is shown as a horizontal line on Fig. 11.
Using the slightly higher IHME mortality rate allows our Fig. 10 predictions to be compared with the most recent IHME predictions5, as shown in Fig. 12. The IHME predictions include the presumption of a 2nd Resurgence, due to factors6 of “seasonality and declining vigilance”. Each IHME projection shown in Fig. 12 is also an IHME Model average5, with the magnitude of their lower and upper bound deviations (not graphed) being < 2 5% by 9/26/2020, increasing to < 42% by 1/1/2021. The IHME 2nd assumptions are evident in the upward (+) curvature in all IHME predictions, as compared to the downward (-) curvature of the present Resurgence model, indicating progress to a CoVID-19 pandemic shut-off, assuming NO 2nd Resurgence occurs.
Ratio of Total # of USA Deaths to Total # of bing.com reported USA CoVID-19 Cases, 3/21/20 through 8/27/2020. Some USA CoVID-19 restrictions lifted ∼6/7/2020 leading to CoVID Resurgence; IHME used 3.1065% as of 8/27/20.
The 8/27/20 IHME 3.1065% Mortality Rate for USA CoVID-19 cases was applied to Fig. 10 to estimate USA CoVID-19 mortality, assuming NO 2nd Resurgence; enabling comparison to IHME’s model, which has 2nd Resurgence effects.
The causes of a 2nd Resurgence could include a large-scale set of new re-openings, creating another rapid rise in CoVID-19 cases, similar to Fig. 9. A follow-on analysis would be needed for this 2nd Resurgence. The possibility of multiple CoVID-19 waves was highlighted early on by the University of Minnesota CoVID-19 team7-8, but each wave was assumed to have minimal overlap. Instead, these results, and the IHME projections (which already includes a 2nd Resurgence), support the idea that USA CoVID-19 evolution is likely to have multiple overlapping waves of Resurgence.
5 Discussion and Conclusions
The Initial Resurgence Model (IRM) for USA CoVID-19 Resurgence, given by Eqs. [3.3a]-[3.3d] and Eqs. [3.6a]-[3.6b] has the γo parameter accounting for the effects of society-wide Social Distancing. Our prior work2 showed that the effects of implementing society-wide shut-downs changed the CoVID-19 pandemic evolution within days of the start of its implementation. Thus, the size of γo likely reflects the degree to which society-wide large gatherings were eliminated. It is a non-local parameter that is generally not part of the traditional SEIR (Susceptible, Exposed, Infection, and Recovered or Removed) pandemic modeling, which are governed by local differential equations.
Our analysis shows that the USA CoVID-19 Resurgence data decreased faster than the IRM model predictions. A similar situation3-4 was seen in the CoVID-19 pandemic evolution in Italy, which was successfully modeled by introducing a second process:
which has an exponentially decaying tail. This second process is independent of the gradually changing tdbl doubling time, which gave rise to the IRM 
parameters.
For USA CoVID-19 Resurgence, an Enhanced Resurgence Model (ERM) was developed to include this second process. This ERM essentially replaces the 
and 
of Eqs. [3.3a]-[3.3b] with:
The necessity of using a second process (δo ≠ 0) to model the USA CoVID-19 Resurgence has a potentially important implication. This δo is a second non-local parameter that may not be part of a traditional SEIR (Susceptible, Exposed, Infection, and Recovered or Removed) pandemic model. Pre- vs Post-Resurgence, what else changed? The most likely explanation is that δo measures the degree to which people wear and wore masks to mitigate and prevent CoVID-19 spread during the Resurgence.
Data Availability
All data used is in the Public Domain or was on the CoVID-19 website maintained by bing.com.
