Distinct regimes of particle and virus abundance explain face mask efficacy for COVID-19

Yafang Cheng, Nan Ma, Christian Witt, Steffen Rapp, Philipp Wild, Meinrat O. Andreae, Ulrich Pöschl, Hang Su
doi: https://doi.org/10.1101/2020.09.10.20190348

Abstract

Airborne transmission is an important transmission pathway for viruses, including SARS-CoV-2. Regions with a higher proportion of people wearing masks show better control of COVID-19, but the effectiveness of masks is still under debate due to their limited and variable efficiencies in removing respiratory particles. Here, we analyze experimental data and perform model calculations to show that this contrast can be explained by the different regimes of abundance of particles and viruses. Because of the large number of particles exhaled during human respiration and vocalization, indoor environments are usually in a particle-rich regime which means that masks cannot prevent the inhalation of large numbers of respiratory particles. Usually, however, only a small fraction of these particles contain viruses, which implies a virus-limited regime where masks can help to keep the number of inhaled viruses below the infectious dose. For SARS-CoV-2, the virus load in the respiratory tract of infectious individuals can vary by 3 to 4 orders of magnitude (5th to 95th percentile), leading to substantial variations in the abundance of airborne virus concentrations and infection risks. Nevertheless, we find that most environments are in a virus-limited regime where masks have a high efficacy in preventing the spread of COVID-19 by aerosol or droplet transmission during short-term exposure. The characteristic contrast between particle-rich and virus-limited regimes explains why face masks are highly efficient in most but not all environments, and why the largest benefits can be achieved by non-linear synergetic effects of combining masks with other preventive measures such as ventilation and social distancing to reduce airborne virus concentrations and the overall risk of infection.

Introduction

Airborne transmission is regarded as one of the main pathways for the transmission of viruses that lead to infectious respiratory deceases, including the severe acute respiratory syndrome coronavirus 2 (SARS- CoV-2) (1), and wearing masks has been widely advocated to minimize transmission and protect people. Though commonly used, the effectiveness of surgical masks is still under debate. Compared to N95 respirators, surgical masks show a higher and more variable penetration rate (e.g., from ∼ 30% to 70%) (2, 3). Given the large number of particles emitted upon respiration and especially upon sneezing or coughing (4), the number of respiratory particles that may penetrate masks is substantial, which is one of the main reasons leading to doubts about their efficacy. Moreover, randomized clinical trials show inconsistent results, with some studies reporting only a marginal benefit or no effect of mask use (5). Thus, surgical masks are often considered to be ineffective. On the other hand, observational data show that regions with a higher percentage of the population wearing masks have better control of the coronavirus disease 2019 (COVID-19) (6-8). So how to explain the contrasting results and apparent inconsistency that masks with relatively high penetration rates may still have a significant impact on airborne virus transmission and the spread of COVID-19? Here, we combine knowledge and results of aerosol science and medical research with recent literature data to explain the contrasts and provide a basis for quantifying the efficacy of face masks.

Results

Abundance regimes and mask efficacy

When evaluating the effectiveness of masks, we want to understand and quantify its effect on the infection probability, Pinf. Assuming every single virus has the same chance to infect people, Pinf can be calculated by Embedded Image in which Psingle represents the infection probability of a single virus and Nv represents the total number of viruses attacking the people (9). For airborne transmission, the infection probability Pinf in a given time period can be plotted as a function of airborne virus concentration, Cv. Figure 1 illustrates such a functional dependence of Pinf on Cv based on the exponential dose response model and scaled by the concentration level Cv,50 at which the probability of infection is 50% (9).

Fig. 1.
Fig. 1. Schematic illustration of different abundance regimes for virus and particles.

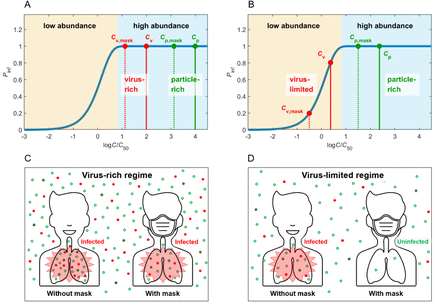
(A) Virus-rich and particle-rich regime; (B) virus-limited and particle-rich regime. The blue line represents the infection probability Pinf under a given ambient virus concentration C. The C50 corresponds to the virus concentration at Pinf of 50%. The Cv and Cp represent the concentration of respiratory viruses and particles, respectively while the Cv,mask and Cp,mask represent their equivalent ambient concentrations after mask use. The shaded areas are separated by a threshold concentration C above which ∼ 100% of people will be infected by viruses. We can see a “virus-rich” regime or a “virus-limited” regime for cases when ambient virus concentration is above or below the threshold, respectively. Under a particle/virus-rich regime, people will always inhale large numbers of particles/viruses and wearing a mask has a limited effect if the resultant concentration is still above the threshold. Under a virus-limited regime, wearing a mask will further reduce the virus concentration and the risk to be infected. (C) and (D) are schematic illustrations for (A) and (B), respectively. Red dots represent respiratory viruses while green dots represent respiratory particles.

Figure 1 shows a highly nonlinear sensitivity of Pinf to the change of virus concentrations. Accordingly, the same percentage change of virus concentration (due to mask use) may lead to different changes in Pinf, i.e., different mask efficiencies. In a virus-rich regime where Cv is much higher than Cv,50 (Figs. 1A and 1C), the probability of infection is close to unity and not sensitive to Cv. In this case, wearing a mask to reduce the inhaled amount by up to a factor of 10 may not suffice to prevent infection. In a virus-limited regime where Cv is close to or lower than Cv,50, however, Pinf varies with Cv, and reducing the inhaled concentration of airborne viruses by wearing a mask will lead to a reduced infection probability (Figs. 1B and 1D). Thus, to understand the mask efficacy, we need to first determine the abundance regime of airborne viruses. In the following, both exhaled and inhaled virus concentrations were examined.

Respiratory particles

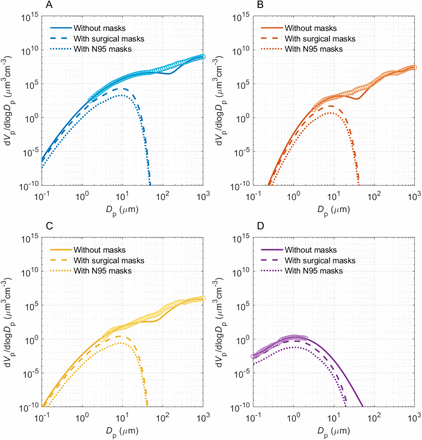
Respiratory particles carrying the viruses are often used to visualize and represent the transmission of airborne viruses (4). We first calculated the regimes for respiratory particles. Figure 2 shows the size distributions of particles emitted by different human respiratory activities (10-12). Taking a representative average of activities given in (13), we find that people can emit a total number of about 3×106 particles during a 30 min period (Sect S1). This extremely large number shows that we are always in a respiratory particle-rich regime. Even after wearing surgical masks, the low collection efficiency still leaves ∼ millions of particles emitted, maintaining a particle-rich regime (green dots in Figs. 1C and 1D). This number is much higher than the virus infectious number, of which the median infectious dose (number) IDv,50 (leading to 50% infection) is estimated to be around a few tens to thousands of viruses for several viruses (14-17). In other words, the human-emitted particle concentration is so high that we cannot avoid inhaling particles generated by another person even when wearing a mask. If every respiratory particle contains one or more viruses, we will be in a virus-rich regime.

Fig. 2.
Fig. 2. Volume size distribution of particles emitted by different human activities.

sneezing (A), coughing (B), speaking (C) and breathing (D) and with and without surgical or N95 masks. Circles represent measurements and solid lines show bimodal fits to measurements. Here, the distribution of exhaled particles for each human activity is also plotted for reference. V and Dp represents the particle volume and diameter, respectively.

Respiratory viruses

But does a respiratory particle-rich regime imply a respiratory virus-rich regime? To answer this question, we investigated the virus distributions in both exhaled samples and inhaled indoor air samples. For exhaled respiratory viruses, as we are not aware of any direct measurement of SARS-CoV-2 emissions, we analyze the recent results for multiple other viruses during a 30-min collection in Leung et al. (2020) (13). This study has a relatively large sample number (246 samples) and diverse virus types (coronaviruses, influenza viruses and rhinoviruses). Moreover, the samples have been collected for both particles above and below ∼ 5 µm, and individual contributions from aerosol mode (< 5 µm) and droplet mode (> 5 µm) particles can be separated. As many samples in Leung et al. (2020) (13) return a virus load signal below the detection limit, we reconstructed the mathematical expectation based on the percentage of positive cases and standard deviation (σ) of virus load distributions (detailed in Sect S2).

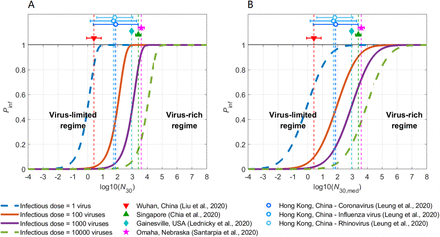
It turns out that most of the time only a minor fraction of exhaled respiratory particles contains viruses. In contrast to the high concentration of respiratory particles, the emitted virus concentration is very low with median Nsample (number of exhaled viruses in a 30-min sample) of ∼ 2.1 for coronaviruses (HCoV-NL63, -OC43, -229E and -HKU1), ∼ 1.6 for influenza viruses (A and B) and ∼ 4.2 for rhinoviruses. Figure 3A shows the dependence of infection probability (Pinf) as a function of the number of viruses under different median infectious dose (IDv,50) (Sect S4). These low Nsample values all fall into a virus-limited regime and are lower than the reported infectious dose (e.g., a few tens to thousands of viruses) for several viruses (14-17). Note that even for a virus number much smaller than the infectious dose, there is still an infectious risk, e.g. Pinf = ∼0.3% for a virus number of 5 and an infectious dose of 1000.

Fig 3.
Fig 3. Abundance regimes for SARS-CoV-2 and other viruses under different infectious dose.

The bold lines show the infection probability (Pinf) as a function of inhaled number of viruses at different median infectious doses. Colored dots show the 30-min inhaled virus numbers (N30) calculated based on reported airborne SARS-CoV-2 concentrations in medical centers/hospitals. Open circles show the 30- min exhaled number of coronavirus, influenza virus and rhinovirus. Error bars show the standard deviation. The virus-rich and virus-limited regime is defined as N30 (Pinf > 0.95) and N30 (Pinf ≤ 0.95), respectively. (A) The infection probability (Pinf) is calculated assuming that each virus has the same probability of causing infection. (B) The infection probability (Pinf) is calculated by considering both the infectious probability of viruses and individual differences (σ = 1) in a large population, in which N30,med represents the effective median 30-min inhaled virus number of the whole population (Sect S4).

For the coronavirus SARS-CoV-2, we examined its virus regime based on N30 (virus number per 30-min inhalation of ∼ 240 L indoor air) in hospitals and health centers, where high concentrations of SARS-CoV- 2 are expected. In Fangcang Hospital in Wuhan, the measured airborne SARS-CoV-2 concentrations varied from undetected to 0.019 L-1 air (18), corresponding to ∼ 0 to 4 viruses per 30-min inhalation. Given a reported infectious dose (hamsters) of < 1000 viruses (17), the human infectious dose is estimated to be ∼ 100 to 1000 for SARS-CoV-2. In this case, a small N30 of ∼ 0 to 4 viruses is likely in a virus-limited regime with Pinf up to ∼0.3% to 3%. N30 of airborne SARS-CoV-2 in U.S. and Singapore medical centers/hospitals have been found to vary from undetected to ∼209-2086 (19-21), corresponding to a high Pinf up to 76% ∼100%, either within or overlapped with the virus-limited regime (Fig. 3A). In an environment of such high virus concentration and Pinf, people may get infected without close contact to patients, and it is a must to use surgical masks and even N95 masks to reduce Pinf.

To link the results of exhalation samples with ambient samples, we design a scenario with patient density, space areas, and ventilation conditions emulating Fangcang Hospital in Wuhan. Under this scenario, we can calculate the ambient concentrations for a given virus emission rate. Based on the emission rates of Leung et al. (2020), we calculated an N30 of undetectable to ∼ 0.72 (5% to 95%) for coronavirus, influenza and rhinovirus in the Fangcang Hospital. Because this concentration range of other viruses overlapped with that of the observed airborne SARS-CoV-2 (N30∼ 0 to 4) in the Fangcang Hospital (18), we expect that the exhaled samples of SARS-CoV-2 may show a similar virus regime as those of other viruses. This result is also supported by recent comparison of viral load in the respiratory tract fluid (22), in which SARS-CoV-2 apparently shows similar viral load to that of influenza B and rhinoviruses.

Variability of viral loads and impact on infection risk and mask efficacy

One notable feature of airborne virus is its highly variable concentrations (several orders of magnitude difference) in indoor environments. On one hand, this is caused by different ventilation, circulation, and sanitization conditions and if emitters were wearing masks. On the other hand, it can be attributed to the large individual differences between different emitters. For exhaled virus numbers reported in Leung et al. (2020) (13), despite of a low median Nsample values of ∼1.2 to 3.6, the maximum Nsample values reached ∼ 4×103 to 4×105 viruses. Such large variability is also consistent with the measured viral load distribution in respiratory tract fluid (22, 23). For example, we can fit their viral load distribution of SARS-CoV-2 by a lognormal distribution with a σ of ∼1 to 2 (Sect S2).

The degree of this variability is a key parameter in the assessment of infectious risks and the selection of protection devices/strategies. As shown Fig. 3B, the broad distribution of virus concentrations also changed the shape of infection probability (Pinf) curve. It expanded the range of virus-limited regimes from N30 < 4.32×IDv,50 (without considering variability, σ = 0) to N30 < 66.1×IDv,50 (considering a variability of σ = 1). As a result, all virus concentrations shown in Fig. 3A falls into a virus-limited regime for infectious doses of ∼ 100 – 1000 viruses. Compared to the case of uniform viral loads (σ = 0), the broad distribution reduced (or increased) the value of Pinf at Pinf above ∼ 0.5 (or below ∼ 0.5), reduced the overall sensitivity of Pinf to the virus concentration, and lead to substantial local variations in virus infection probability. Besides, the large variability also suggests that the limited sample numbers of virus measurements commonly used may introduce uncertainties to the assessment, which may explain why early studies that have investigated whether masks reduce infection in randomized controlled trials obtained results that were partly inconsistent (Fig. S3B) (24-27).

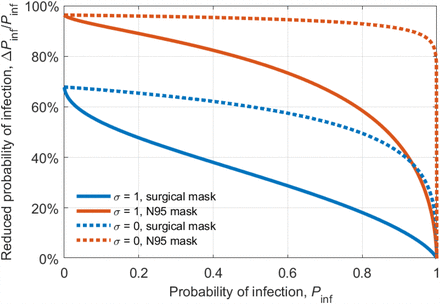
Figure 4 shows the reduced chance of COVID-19 transmission with surgical and N95 masks calculated from Fig. 3, i.e., the percentage change of Pinf due to the change of N30 caused by mask uses. It is commonly assumed that the percentage change of Pinf is proportional to the percentage change of N30. In this way, wearing the same mask will have the same impact on the virus transmission at any Pinf. However, our analysis shows a nonlinear effect of mask uses on the virus transmission, which strongly depends on the present infection probability, Pinf, or N30. As shown in Fig. 4, at high Pinf, wearing masks has a minor effect on Pinf while at low Pinf, wearing masks becomes very efficient. Figure 4 also shows the impact of broad virus distributions on the mask efficacy, i.e., it greatly reduces the efficiency of masks (solid lines) compared to the case of uniform viral load (dash lines).

Fig. 4.
Fig. 4. Reduced chance of COVID-19 transmission with masks.

The curves represent the percentage change of the probability of infection, Pinf, caused by mask use due to the change of N30. The blue and red lines represent the results with surgical (blue lines) and N95 masks (red lines), respectively. The dependence of Pinf on N30 used here was assumed the same as in Fig. 3.

According to the ratio of the reproduction rate (∼2-7) for SARS-CoV-2 to the average daily contact number (∼10-25) (28, 29), we can estimate an upper limit of the effective Pinf of ∼ 10% to 70% for airborne transmission in large populations, suggesting the ubiquity of a virus-limited regime for SARS-CoV-2. As shown in Fig. 4, in this range of Pinf, wearing masks (both surgical and N95 masks) may largely reduce the chance of COVID-19 transmission. This is consistent with the results of 172 observational studies across 16 countries and six continents which have shown a large reduction in risk of infection by face mask use (7). More importantly, the increasing effectiveness of mask use at lower Pinf and N30 suggests synergistic effects of multiple preventive measures in reducing the infection risk.

Aerosol transmission vs droplet transmission

Concerning the relative importance of aerosol mode vs droplet mode, we find that the aerosol mode, despite of much smaller particle volumes, shows a virus number similar to or even slightly higher than that of the droplet mode for both ambient and exhaled samples: N30 (aerosol mode vs droplet mode) of ∼5.1 vs ∼1.4 for SARS-CoV-2 in the Fangcang Hospital (Table S7); and Nsample (aerosol mode vs droplet mode) of 1.4 vs 0.68 for coronaviruses (HCoV-NL63, -OC43, -229E and -HKU1), of 1.2 vs 0.43 for influenza viruses (A and B) and of 3.6 vs 0.63 for rhinoviruses, respectively. This suggests a much higher virus load per particle volume in the aerosol mode than that in the droplet mode. Because the amount of bioaerosols or compounds delivered in particles is proportional to its concentration in the bulk fluid used to generate the particles, and is independent of the investigated particulate type (30). If the aerosol and droplet modes are mainly generated from the lower and upper respiratory tracts respectively (31), the higher concentration of viruses in the lung fluid (i.e., sputum samples show much higher viral load than throat and nasal swabs (23)) may explain the high virus concentration in the aerosol mode.

Discussion

The abundance regimes, size dependence, and individual differences have important implications in epidemic prevention. The large fraction of virus in the aerosol mode suggests a higher risk than expected, because small particles have a longer lifetime in the air and thus can accumulate to a threshold infection level. This also shows that the greatest danger is in spaces with large number of people and poor ventilation, where virus accumulates in the air over long times. Long period of release, long residence time, and long period of exposure combine to maximize risks. Besides, aerosol mode particles also have a higher penetration rate, and probability to reach the lower respiratory tract (e.g., lung) (32, 33), we thus expect that the aerosol mode can cause more severe infectious symptoms than the droplet mode particles in view of the infection mechanism/nature of SARS-CoV-2.

However, our results show that the airborne transmission of SARS-CoV-2 is most likely in a virus-limited regime. In this regime, any preventive measure (such as wearing masks, ventilation, social distancing) that reduces the inhaled particles concentrations will reduce the infection probability. The increasing efficiency of preventive measures at lower virus concentration also suggests that the more measures used, the more effective each measure will be in containing the virus transmission. For example, when both sources (infector) and susceptible people were wearing masks, the inhaled virus concentration will be further reduced, thereby further improving the efficacy of the mask and forming positive feedback. Besides, because the inhaled dose also affects the severity of the infection (17), masks can still be useful even if the reduced dose still leads to an infection. The differences between abundance regimes are not limited to respiratory particles and viruses, but may also exist between different types of viruses. Viruses of higher emission/exhalation rates, longer lifetime and lower infectious dose may result in a virus-rich regime and thus a high basic reproduction number (most likely in the case of measles (34)). Note that in this study we focused our discussions on airborne respiratory particles < 100 µm. Respiratory particles > 100 µm can carry more viruses, e.g., a single one-millimeter droplet may carry ∼50,000 viruses given a viral load of 1×108 per milliliter respiratory droplet, higher than the estimated infectious dose of SARS- CoV-2. Though they will be removed from air in seconds through fast gravitational settling, they may still be sprayed into the upper respiratory tract of susceptible people in a close contact, and leads to infections. Concerning these super large droplets, masks become even more efficient and can remove ∼100% of them.

The orders-of-magnitude differences in emitted virus concentrations between individuals suggest that some patients can emit far more viruses and become super spreaders. According to Wölfel et al. (2020) (23), pharyngeal virus shedding was very high during the first week of symptoms. The large variability also suggests that even if the median value is in a virus-limited regime, an individual patient, i.e., a super spreader, may still create a virus-rich regime, where wearing surgical masks would provide insufficient protections. To better deal with such cases, stricter measures, including wearing N95 masks become critical in preventing virus transmission. This is also supported by the fact that wearing N95 masks (and eye protection) leads to a low rate of infection despite of close contact with infectious people (among the 40000 medical staffs, almost no one got infected when wearing N95 masks in Wuhan, http://www.ccdi.gov.cn/yaowen/202003/t20200323_214056.html).

Airborne virus concentration, virus load in respiratory tract fluid, and human emitted virus concentrations are key parameters in our understanding of generation and airborne transmission mechanisms of viruses. Our preliminary quantitative analysis shows a high potential in achieving closures between these parameters, which is essential toward a mechanistic understanding. Such a closure study will ideally require simultaneous measurements of these parameters, which is not available at the moment and is desirable in future research.

Materials and Methods

Modelling of indoor airborne virus concentrations

To compare the results of exhalation samples with indoor air samples, we performed model simulations for a scenario with patient density, space areas, and ventilation conditions emulating Fangcang Hospital in Wuhan:

  • The total area of the ward is 500 m2 with a height of 10 m. The total number of patients is 200 (18).

  • Each patient coughed an average of 34 times per hour, and the volume of each cough is 2 L; the breath volume is 8 L min-1. The size distributions of particles emitted during coughs and breath were taken from Fig. 2.

  • All patients were wearing surgical masks with penetration rates given in Fig. S1A according to the guideline of Fangcang Hospital (https://edition.cnn.com/2020/02/22/asia/china-coronavirus-roundup-intl-hnk/index.html). We have also calculated the case when the patients did not wear any mask.

  • Natural ventilation is assumed and the loss rate of particles is calculated according to the function given in Fig. S2 (35).

The median viral load in exhaled samples were assumed the same as in Leung et al. (2020) (13) (Sect S2) and the variation between individual patients was assumed to follow a lognormal distribution with a σ of 1. After being emitted, respiratory particles lose water and is dried to half of their initial sizes (36).

The indoor airborne virus concentration can be calculated with 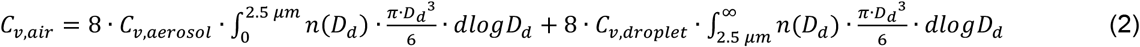Embedded Image where, Cv,aerosol and Cv,droplet are the viral loads in aerosol mode and droplet mode, respectively; Dd is the particle dry diameter; n(Dd) is the equilibrium indoor airborne particle number size distribution and can be determined by 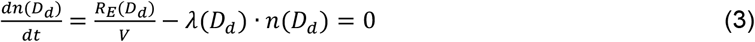Embedded Image where RE is the emission rate of particles by all patients; V is the volume of the ward; and λ is particle loss rate due to ventilation and deposition.

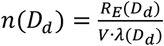In the case when all patients were wearing surgical masks, Embedded Image where, RE0 is the emission rate of patients without wearing mask, Dw is the wet diameter of exhaled droplets, Pmask is size-resolved particle penetration rate of surgical masks. In this case, we assumed that exhaled liquid droplets only start to lose water after penetrating masks. In case no patients wearing masks, RE(Dw) = RE0(Dw). Based on Eq. (3), the ambient particle number size distribution can be calculated as Embedded Image when reaching equilibrium.

To account for the individual differences of viral load in exhaled particles, a Monte Carlo method is used to get the possible values of airborne virus concentration. The calculation is repeated for 1×107 times with randomly generated viral load, which follow a lognormal distribution with a σ of 1. The calculated indoor airborne concentrations of coronavirus, influenza virus and rhinovirus are listed in Table S1.

Our calculation does not consider the lifetime of viruses (37). With a fixed virus emission rate, the airborne virus concentration is proportional to 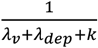Embedded Image, where λv, λdep and k are loss rates due to ventilation, deposition and virus inactivation, respectively. The value of k is similar as (or smaller than) λv and λdep (38). Therefore, ignoring virus loss due to inactivation (k) has a minor effect on the calculated airborne virus concentrations. The other caveat is that the particle loss rate (λv + λdep) used here may differ from the real loss rate in Fangcang Hospital. According to the loss rate reviewed by Thatcher et al. (2002) (39), we may expect a maximum uncertainty of one order of magnitude in the calculated airborne virus concentrations, which will not change the regimes they belong to.

Penetration rate of masks

The size-resolved particle penetration rate of surgical and N95 masks (Fig. S1) is calculated based on the following literature and model calculation:

  • Particle diameter < 800 nm: modified from Grinshpun et al. (2009) (40)

  • Particle diameter > 800 nm & < 5µm: modified from Weber et al. (1993) (41)

  • Particle diameter > 5µm: model calculation based on particle impaction with following parameters:

    • Droplets velocity of 6.5 m s-1, calculated based on the volume flow rate of 8 L min-1 (typical breath flow rate of adults) and an air flow cross section as a circle with a diameter of 1 cm;

    • Impact angle = 90 degree.

Sample numbers and uncertainties

We found that the huge variability of the patient’s exhaled virus concentration is an important reason for the contrast conclusions from experiments on efficacy of masks to prevent virus transmissions. This large variability requires a large number of samples to draw a robust conclusion. To illustrate the impact of the number of samples, a sensitivity experiment is conducted using a Monte Carlo approach: the virus number in samples of 30-min exhaled droplets above and below 5 µm is assumed to follow a lognormal distribution with median values as given in Table S3 and a σ of 1. The sampling experiment is simulated with different sample numbers (2, 5, 10, 20, 50, 100, 200, 500 and 1000) and each experiment is repeated for 1×104 times. The standard deviation (σ) of the derived positive rates (percentage of samples with virus number > 2 (13)) is then calculated. Moreover, to see how the sample number influences the evaluation of the efficacy of masks, the virus number is calculated with a pre-assumed set of positive rates which follow a normal distribution with σ shown in Fig. S3A. The frequency distributions of derived virus number in 30-min exhalation samples with and without masks at different sample numbers are given in Fig. S3B.

Figure S3A shows the variability of the positive rates under different number of samples. And Fig. S3B shows the frequency distributions of the calculated virus numbers under different sample numbers. When the number of samples is less than 10, the uncertainty of the observed positive rate is relatively large (σ up to ∼0.35), and the difference between the derived viral load in samples collected with and without mask use have a high chance to be indistinguishable (Fig. S3B). When the number of samples is ∼ 100, the variability is small (σ ∼ 0.05), and the efficacy of masks become visible.

Data Availability

All data is available in the main text or the supplementary materials.

Footnotes

  • Competing Interest Statement: Authors declare no competing interests.

References

  1. 1.↵
    L. Morawska, D. K. Milton, It is Time to Address Airborne Transmission of COVID-19. Clinical Infectious Diseases doi:10.1093/cid/ciaa939 (2020).
    OpenUrlCrossRefPubMed
  2. 2.↵
    S. A. Grinshpun et al., Performance of an N95 Filtering Facepiece Particulate Respirator and a Surgical Mask During Human Breathing: Two Pathways for Particle Penetration. Journal of Occupational and Environmental Hygiene 6, 593–603 (2009).
    OpenUrlCrossRefPubMedWeb of Science
  3. 3.↵
    T. Oberg, L. M. Brosseau, Surgical mask filter and fit performance. American Journal of Infection Control 36, 276–282 (2008).
    OpenUrlCrossRefPubMedWeb of Science
  4. 4.↵
    L. Bourouiba, Turbulent Gas Clouds and Respiratory Pathogen Emissions: Potential Implications for Reducing Transmission of COVID-19. Jama 323, 1837–1838 (2020).
    OpenUrlCrossRefPubMed
  5. 5.↵
    A. E. Aiello et al., Mask use, hand hygiene, and seasonal influenza-like illness among young adults: A randomized intervention trial. The Journal of Infectious Diseases 201, 491–498 (2010).
    OpenUrlCrossRefPubMedWeb of Science
  6. 6.↵
    T.-C. Hsiao, H.-C. Chuang, S. M. Griffith, S.-J. Chen, L.-H. Young, COVID-19: An Aerosol’s Point of View from Expiration to Transmission to Viral-mechanism. Aerosol and Air Quality Research doi:10.4209/aaqr.2020.04.0154, 905–910 (2020).
    OpenUrlCrossRef
  7. 7.↵
    D. K. Chu et al., Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. The Lancet 395, 1973–1987 (2020).
    OpenUrlCrossRef
  8. 8.↵
    R. Zhang, Y. Li, A. L. Zhang, Y. Wang, M. J. Molina, Identifying airborne transmission as the dominant route for the spread of COVID-19. Proc. Natl. Acad. Sci. 117, 14857–14863 (2020).
    OpenUrlAbstract/FREE Full Text
  9. 9.↵
    C. N. Haas, J. B. Rose, C. P. Gerba, Quantitative microbial risk assessment. John Wiley & Sons, (1999).
  10. 10.↵
    C. Y. H. Chao et al., Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Journal of aerosol science 40, 122–133 (2009).
    OpenUrlCrossRefPubMedWeb of Science
  11. 11.
    J. P. Duguid, The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. The Journal of hygiene 44, 471–479 (1946).
    OpenUrlCrossRefPubMed
  12. 12.↵
    H. Holmgren, E. Ljungström, A.-C. Almstrand, B. Bake, A.-C. Olin, Size distribution of exhaled particles in the range from 0.01 to 2.0μm. Journal of Aerosol Science 41, 439–446 (2010).
    OpenUrlCrossRefWeb of Science
  13. 13.↵
    N. H. L. Leung et al., Respiratory virus shedding in exhaled breath and efficacy of face masks. Nature Medicine 26, 676–680 (2020).
    OpenUrlCrossRefPubMed
  14. 14.↵
    K. A. Callow, H. F. Parry, M. Sergeant, D. A. J. Tyrrell, The time course of the immune response to experimental coronavirus infection of man. Epidemiology and Infection 105, 435–446 (1990).
    OpenUrlCrossRefPubMed
  15. 15.
    T. Watanabe, T. A. Bartrand, M. H. Weir, T. Omura, C. N. Haas, Development of a Dose-Response Model for SARS Coronavirus. Risk Analysis 30, 1129–1138 (2010).
    OpenUrlCrossRefPubMed
  16. 16.
    A. Roberts et al., Severe Acute Respiratory Syndrome Coronavirus Infection of Golden Syrian Hamsters. Journal of Virology 79, 503–511 (2005).
    OpenUrlAbstract/FREE Full Text
  17. 17.↵
    M. Imai et al., Syrian hamsters as a small animal model for SARS-CoV-2 infection and countermeasure development. Proc. Natl. Acad. Sci. 117, 16587–16595 (2020).
    OpenUrlAbstract/FREE Full Text
  18. 18.↵
    Y. Liu et al., Aerodynamic analysis of SARS-CoV-2 in two Wuhan hospitals. Nature 582, 557–560 (2020).
    OpenUrlPubMed
  19. 19.↵
    P. Y. Chia et al., Detection of air and surface contamination by SARS-CoV-2 in hospital rooms of infected patients. Nat. Commun. 11, 2800 (2020).
    OpenUrlCrossRef
  20. 20.
    J. L. Santarpia et al., Aerosol and Surface Transmission Potential of SARS-CoV-2. medRxiv 10.1101/2020.03.23.20039446, 2020.2003.2023.20039446 (2020).
  21. 21.↵
    J. A. Lednicky et al., Collection of SARS-CoV-2 Virus from the Air of a Clinic within a University Student Health Care Center and Analyses of the Viral Genomic Sequence. Aerosol and Air Quality Research 20, 1167–1171 (2020).
    OpenUrl
  22. 22.↵
    D. Jacot, G. Greub, K. Jaton, O. Opota, Viral load of SARS-CoV-2 across patients and compared to other respiratory viruses. Microbes and Infection https://doi.org/10.1016/j.micinf.2020.08.004 (2020).
  23. 23.↵
    R. Wölfel et al., Virological assessment of hospitalized patients with COVID-2019. Nature 581, 465–469 (2020).
    OpenUrlCrossRefPubMed
  24. 24.↵
    C. R. MacIntyre et al., Efficacy of face masks and respirators in preventing upper respiratory tract bacterial colonization and co-infection in hospital healthcare workers. Preventive medicine 62, 1–7 (2014).
    OpenUrlCrossRefPubMed
  25. 25.
    C. R. MacIntyre et al., A randomized clinical trial of three options for N95 respirators and medical masks in health workers. American journal of respiratory and critical care medicine 187, 960–966 (2013).
    OpenUrlCrossRefPubMed
  26. 26.
    M. Loeb et al., Surgical mask vs N95 respirator for preventing influenza among health care workers: a randomized trial. Jama 302, 1865–1871 (2009).
    OpenUrlCrossRefPubMed
  27. 27.↵
    L. J. Radonovich, Jr. et al., N95 Respirators vs Medical Masks for Preventing Influenza Among Health Care Personnel: A Randomized Clinical Trial. Jama 322, 824–833 (2019).
    OpenUrlCrossRefPubMed
  28. 28.↵
    J. Zhang et al., Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368, 1481–1486 (2020).
    OpenUrlAbstract/FREE Full Text
  29. 29.↵
    S. Y. Del Valle, J. M. Hyman, H. W. Hethcote, S. G. Eubank, Mixing patterns between age groups in social networks. Social Networks 29, 539–554 (2007).
    OpenUrlCrossRefWeb of Science
  30. 30.↵
    M. O. Fernandez et al., Assessing the airborne survival of bacteria in populations of aerosol droplets with a novel technology. Journal of The Royal Society Interface 16, 20180779 (2019).
    OpenUrl
  31. 31.↵
    B. Bake, P. Larsson, G. Ljungkvist, E. Ljungström, A. C. Olin, Exhaled particles and small airways. Respiratory Research 20, 8 (2019).
    OpenUrlPubMed
  32. 32.↵
    W. G. Kreyling, M. Semmler-Behnke, W. Möller, Health implications of nanoparticles. Journal of Nanoparticle Research 8, 543–562 (2006).
    OpenUrl
  33. 33.↵
    W. G. Kreyling, M. Semmler-Behnke, W. Möller, Ultrafine particle-lung interactions: does size matter? Journal of aerosol medicine : the official journal of the International Society for Aerosols in Medicine 19, 74–83 (2006).
    OpenUrl
  34. 34.↵
    F. M. Guerra et al., The basic reproduction number R0 of measles: a systematic review. The Lancet Infectious Diseases 17, e420–e428 (2017).
    OpenUrlCrossRefPubMed
  35. 35.↵
    J. Zhao et al., Particle Mass Concentrations and Number Size Distributions in 40 Homes in Germany: Indoor-to-outdoor Relationships, Diurnal and Seasonal Variation. Aerosol and Air Quality Research 20, 576–589 (2020).
    OpenUrl
  36. 36.↵
    M. Nicas, W. W. Nazaroff, A. Hubbard, Toward Understanding the Risk of Secondary Airborne Infection: Emission of Respirable Pathogens. Journal of Occupational and Environmental Hygiene 2, 143–154 (2005).
    OpenUrlCrossRefPubMedWeb of Science
  37. 37.↵
    N. van Doremalen et al., Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. New England Journal of Medicine 382, 1564–1567 (2020).
    OpenUrlCrossRefPubMed
  38. 38.↵
    S. L. Miller et al., Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. MedRxiv, (2020).
  39. 39.↵
    T. L. Thatcher, A. C. K. Lai, R. Moreno-Jackson, R. G. Sextro, W. W. Nazaroff, Effects of room furnishings and air speed on particle deposition rates indoors. Atmospheric Environment 36, 1811–1819 (2002).
    OpenUrlCrossRefWeb of Science
  40. 40.
    S. A. Grinshpun et al., Performance of an N95 filtering facepiece particulate respirator and a surgical mask during human breathing: two pathways for particle penetration. Journal of occupational and environmental hygiene 6, 593–603 (2009).
    OpenUrlCrossRefPubMedWeb of Science
  41. 41.
    A. Weber et al., Aerosol penetration and leakae characteristics of masks used in the health care industry. American Journal of Infection Control 21, 167–173 (1993).
    OpenUrlCrossRefPubMedWeb of Science
Back to top
Posted December 16, 2020.
Download PDF

Supplementary Material

Data/Code
Email
Distinct regimes of particle and virus abundance explain face mask efficacy for COVID-19
Yafang Cheng, Nan Ma, Christian Witt, Steffen Rapp, Philipp Wild, Meinrat O. Andreae, Ulrich Pöschl, Hang Su
medRxiv 2020.09.10.20190348; doi: https://doi.org/10.1101/2020.09.10.20190348
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area