Abstract
It is now recognized that aerosol transport contributes to the transmission of the SARS-CoV-2. Existing social distancing guidelines are given in terms of distance, with vague statements about contact times. Also, estimates of inhalation of virus in a contaminated space typically assume a well-mixed environment, which is realistic for some, but not all, situations. We consider a local casual interaction of an infected individual and a susceptible individual, both maskless, account for the air flow and aerosol transport characteristics of speaking and breathing, and propose guidelines that involve both space and contact time, based on a conservative model of the interactions.
I. INTRODUCTION
Transmission of COVID-19 during the presymptomatic and asymptomatic stages are estimated to be responsible for more than half of the overall transmission [1, 2]. The recognition that aerosols play a significant role in the transmission of SARS-CoV-2 raises the issue of quantifying the air exchange between asymptomatic individuals, who are sources of the virus, and healthy individuals, who are susceptible to infection. A common model for characterizing this situation is to estimate the probability of infection based on the number N of virions inhaled, relative to a characteristic dose Ninf that, on average, produces infection; the corresponding probability of infection p is then estimated as [3]

Past studies provide insights into the risk of infection by performing room-scale averages of the virion concentration, e.g. [4]. Recent studies applied to SARS-CoV-2 have similar features and allow an estimate of the number of inhaled virions by a susceptible individual in a space, e.g., bathroom, airplane, laboratory, etc. [5–7]. Such well mixed models are appropriate when the asymptomatic source individuals are well removed from healthy individuals so that the time scale to mix in the environment is faster than the time for direct exchange of air between a source and a receiver.
Here, we are concerned with the casual conversations in a social setting, where local air exchange between individuals is the dominant factor in determining the infection probability. There are earlier studies characterizing qualitative features of the respiratory flow between two people using numerical simulations and experiments with mannequins [8, 9] and a recent study using a numerical model to probe spatial features of drop and aerosol transport between a two people where one is an infected speaker [10]. We consider a poorly ventilated environment, in which the separation distance between an asymptomatic speaker and a healthy interlocutor is comparable to those recommended by the World Health Organization (1 m) and the Center for Disease Control (CDC) in the United States (2 m). Indeed, we can imagine that such local, air flow-driven virus exchange may occur in conversations at parties, across the table at lunch or in a conference room, on a train, etc. Recent estimates provide Ninf ≈ 100 − 1000 and, consistent with other modeling efforts, below we take the conservative value Ninf = 100 [5, 6, 11]. We assume the transport of aerosolized virions is that of a passive scalar, as justified below, and use a model of the time and space dependence of air flow in speech from our recent work [12]. These assessments should be combined with other global estimates to better understand the possible dynamics of virus exchange in different situations, in the absence of wearing a mask.
II. MODEL OF AIR FLOW DURING SPEECH AND VIRUS UPTAKE UPON INHALATION
II.1. Conical, quasi-steady air flows characterize exhalation during speech
Utilizing laboratory experiments of the air flow during speaking, numerical simulations of the Navier-Stokes equations for pressure-driven flows from an orifice, which mimics speech, and a mathematical model of these dynamics, our recent work [12] has shown that maskless speaking and breathing in poorly ventilated environments can produce a conical quasi-steady, turbulent jet after a few seconds, as shown in Fig. 1. Sufficiently far away from the mouth, the unsteadiness of the inhaling/exhaling signal is barely visible and the jet behaves similar to a turbulent jet with constant inflow. A typical laboratory measurement of the flow field produced by breathing is displayed in Fig. 1(a), while a simulation of the air flow produced by speaking is shown in Fig. 1(b). The typical cone half angle α is about 10 − 14°. Hence, the area of the cone will envelop the size of a human head already at 50 cm separation distance. In the simulation shown in Fig. 1(b), we highlight a concentration contour, c = 0.05 (with c = 1 at the mouth), which is comparable to the scale of the head a distance 1.6 m away (the right limit of the figure). Hence, non-negligible exhaled concentrations are found at distances comparable to social interactions.
Conical flows from breathing and speech, (a) Flow visualization of the conical jet produced by breathing from the mouth, adapted from Ref. [12]. Speaking can produce similar conical jets. The cone angle is 2α. A (susceptible) receiver is facing the asymptomatic (infected) breather/speaker at a distance is ℓ. (b) Simulated transport of exhaled material during repeated speech. Results of numerical simulations from Ref. [12]: example of the instantaneous field of a passive scalar used to visualize the dilution of the air exhaled from an infected speaker, displayed over a vertical symmetry plane after 9.5 cycles of periodic speaking-inhaling (each cycle lasts 4 s), with a volume per breath of 0.75 L. The color map shows the concentration field c of the passive scalar with c = 1.0 at the exit of the mouth and c = 0 in the ambient far-field (the scale is saturated here to better visualize the field close to the receiver). An iso-concentration line at c = 0.05 is displayed to help quantify the dilution levels far from the mouth of the speaker to the left. We sketch a head of a person breathing at the right (roughly sized to the scale of the figure), as an illustration of the inhalation that occurs when another individual enters this concentration field. Both scale bars are 10 cm.
We note that our experiments in ventilation-poor environments show that during speaking the effect of buoyancy at the scale of a few meters of jet motion (Fig. 1(a)) does not cause a substantially vertical motion beyond the size of a human head. Moreover, due to entrainment of the surrounding air, the thermal signature will decay inversely with distance, comparable to a passive scalar such as an aerosol, as discussed below, which further diminishes the buoyancy effects.
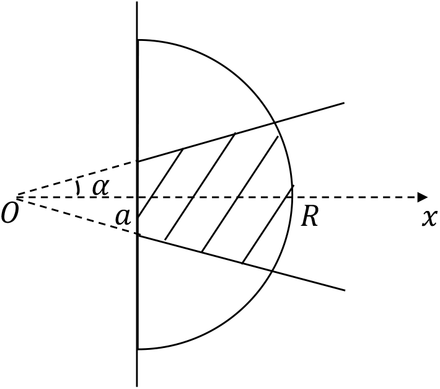
Because of the relatively high Reynolds numbers (Re ≈ 100 − 1000), the expiratory flow is approximately jet-like and entrains surrounding air, while the inhalatory flow is approximately hemi-spherical, as sketched in Fig. 2; see [12]. As a consequence of the asymmetry of inhaling/exhaling, only a small portion of the inhaled breath comes from the exhaled material of the same individual. This may easily be verified by a simple model: if we assume the volume of air inhaled and exhaled in one breathing cycle is the same, denoted by V, then the radius R of the inhaled hemisphere is R = (3V/2π)1/3. In the volume to inhale, only a small conical portion (the shaded region in Fig. 2) is occupied by the exhaled material, whose volume is Ve ≈ π[(R + a cot α)3tan2 α − a3cot α]/3. Using V = 0.5 L [13] and α = 12°, we have Ve/V ≈ 0.1. Indeed, exploiting the series of numerical simulations of periodic breathing and speaking of a single individual published in Ref. [12], we confirmed this ratio of 10% of the exhaled material from one breath inhaled in the next inspiration. This was for an elliptic mouth of radii 1 cm and 1.5 cm, with a fixed cycle duration of 4 s, for very different flow rate signals, and a volume per breath between 0.5 L and 1.0 L. This means that when a person inhales, they mainly inhale the surrounding air. It is thus the environment around the head of the (healthy) person that needs to be characterized to develop an estimate of the risk of virus uptake in these close encounters.
Sketch of ideal respiratory flow regions. The expiratory flow region is a cone with half-angle α and apparent origin at O. The mouth is modelled as a circle of radius a, located at x = a cot α. The inhalatory flow region is a hemisphere with radius R (determined by the inhaled volume, see text) and centered at x = a cot α (the mouth exit). In the inhaled volume, only the shaded region is from the previous exhalation.
When an asymptomatic subject exhales or speaks, small droplets carrying virus can spread to a receiving interlocutor; the drop size distribution [5, 14–17] and the influence of loudness and phonetic features on droplet production rates [18–20] have been measured. In this paper, we use these quantities, along with the flow field characteristics sketched above, to quantify the amount of virus that will reach the receiver in a poorly ventilated space, and so provide a measure of the risk of infection. The model allows quantitative assessment of the impact of separation distance and time of interaction.
Experiments show that it takes 30 to 50 seconds for the jet to reach a distance 3 m for steady speaking [12]; the jet can reach 2 m in even 20 s. The radii of droplets produced by speaking are found to be typically around or smaller than 5 μm, e.g., see the recent experiments [5, 16, 17]; drops of smaller sizes are usually categorized as aerosols. It takes about 0.1 s for a water droplet of radius 5 μm (and about 2 s for radius 20 μm) to evaporate at a relative humidity of 0.5 [21], so most small droplets produced by speaking should evaporate rapidly to become aerosol particles at the beginning of the jet spreading. During Δt = 50 s, an aerosol particle of radius rp = 1 μm and density ρp = 103 kg/m3 sediments a distance of  , where g = 9.8 m2/s is the gravitational acceleration and μa = 1.8 × 10−5 Pa·s is the viscosity of air. Therefore, at the scale of a social interaction, we treat the aerosol particles as passive tracers that follow the jet flow.
, where g = 9.8 m2/s is the gravitational acceleration and μa = 1.8 × 10−5 Pa·s is the viscosity of air. Therefore, at the scale of a social interaction, we treat the aerosol particles as passive tracers that follow the jet flow.
II.2. Inhalation and an estimate of risk from virus inhalation
We now calculate the susceptible receiver’s virion uptake by neglecting the receiver’s self-induced flow field, from breathing and/or speaking, on the ambient concentration field in the environment. This is a conservative estimate for the worst-case scenario, when (1) the infected individual speaks continuously and the susceptible individual only listens (and breathes) and (2) the receiver breathes through the nose; in that case, the exhaled flow is downwards [13] and its impact on the conical jet from the infected individual is assumed negligible. These assumptions also apply to a susceptible individual that joins a group and stands opposite an asymptomatic person who has been speaking for some time.
The speaker’s mouth can be approximated as a circle with radius a. Denoting the cone angle as 2α, the cross-sectional area of the jet beyond the mouth A(x) = π(x tan α)2, where x is the spatial axis from the cone vertex as shown in Fig. 1. In a steady jet, the momentum flux, which is proportional to υ2(x)A(x), is constant, where υ(x) is the average velocity in the jet. Therefore υ(x) = υ0a/x tan α, where υ0 is the flow velocity at the mouth. Denoting the virus concentration in the saliva of the asymptomatic speaker as cυ (number virions/volume saliva) and the volume fraction of droplets at the mouth as ϕ0 (volume droplets/volume air), then the total droplet volume production rate in speaking is j0 = πa2υ0ϕ0 (volume droplets/time). It follows that the total emission rate of virus is I0 = cυj0 (number virions/time). Within a quasi-steady approximation [12], and denoting ϕ(x) as the volume fraction of droplets in the jet, the flux of virus in the steady jet cυϕ(x)υ(x)A(x) is also constant and equal to I0. Thus, we conclude ϕ(x) = ϕ0a/x tan α.
We now consider a susceptible individual at a distance ℓ in front of an infected speaker (Fig. 1). Assuming the average inhalation volume flux of the receiver (at x = ℓ) to be Qr, then the intake dose of the receiver is
 over a period of time t. This result does not depend explicitly on the speed of the air flow. Also, we note that as the droplets evaporate cυ will increase and ϕ(x) will decrease, however, the virus concentration cυϕ(x) (number virions/volume air) is unaffected by evaporation.
over a period of time t. This result does not depend explicitly on the speed of the air flow. Also, we note that as the droplets evaporate cυ will increase and ϕ(x) will decrease, however, the virus concentration cυϕ(x) (number virions/volume air) is unaffected by evaporation.
Typical values related to speaking reported in the literature.
Typical values of the variables in equation (2) are summarized in table I. The typical range of ϕ0 is calculated from table I to be 2 × 10−9 − 1 × 10−8. Note that I0 in breathing has been measured by collecting respiratory droplets and aerosols in 30 min from infected people [22]. The average value is around 300 min−1, which is smaller than I0 in speaking, and estimated by I0 = cυj0 using the values in table I. For an average (infected) patient (cυ= 7 × 106 mL−1, υ0 = 3 m/s), I0 ≈ 1 × 103 − 5 × 103 min−1. For a “superspreader” [23] (cυ = 2 × 109 mL−1, υ0 = 3 m/s), I0 ≈ 3 × 105 − 1.5 × 106 min−1.
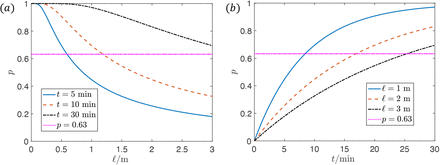
Although the typical “infectious dose” of SARS-CoV-2 is unknown, estimates have been provided. Consistently with other studies, we approximate Ninf conservatively as Ninf = 100 [5, 6]. Based on this criterion and equation (2), we can plot the probability of infection p versus distance ℓ and time t as shown in Fig. 3. The results show the importance of distancing and decreasing contact time in the prevention of transmission of SARS-CoV-2. We use the probability p(N = Ninf) = 1 − e−1 = 0.63 as the boundary between low- and high-risk regions. From Fig. 3, a distance of ℓ = 1 m can maintain a low risk for an interaction of only 5 min, but is not sufficient for an interaction of 10 min, which requires at least 1.5 m; for ℓ = 2 m, the interaction time should be restricted to less than 15 min. We remind the reader that these estimates are based on a single maskless infected individual in a poorly ventilated space (using average virus parameters reported in the literature).
Dependence of infection probability p on (a) distance ℓ and (b) speaking time t. Values of ℓ or t for each curve are given in the legends. The spatial distance is truncated at 3 m, over which we expect the ambient flows become important even in a poorly ventilated space [12]. Other parameters are listed in table II. The plots are for a susceptible individual interacting with a single maskless asymptomatic speaker in a poorly ventilated space.
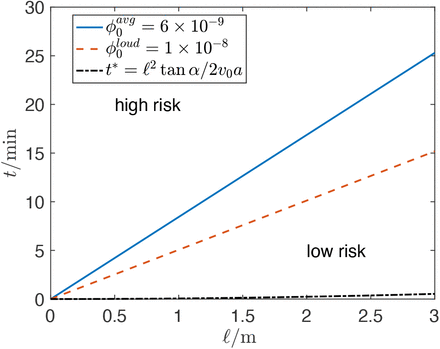
Next, we present a space-time diagram of infection risks in Fig. 4, using N = Ninf as the criterion for high and low risks. This figure represents a proposal for a space-time characterization of social distancing guidelines in a poorly ventilated space with a single asymptomatic speaker. Experiments show that the production rates of droplets increases with the loudness of speech [18–20], which is approximately examined in the figure by using 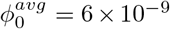 (typical speech) and
(typical speech) and 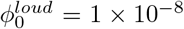 (loud speech). We observe that for ℓ = 2 m and
(loud speech). We observe that for ℓ = 2 m and 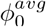 , it should be relatively safe to speak with an asymptomatic individual for less than 15 min, but with loud speech
, it should be relatively safe to speak with an asymptomatic individual for less than 15 min, but with loud speech 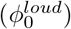 for less than 10 min. According to this model, when talking over 25 min, there is a high risk of infection even at a separation distance of 3 m.
for less than 10 min. According to this model, when talking over 25 min, there is a high risk of infection even at a separation distance of 3 m.
We note that for a speech-driven flow, the time for the jet to reach a distance ℓ is t*(ℓ) = ℓ2 tan α/2υ0a [12]. In Fig. 4, the region below t* is therefore a “no-risk” region since there has not been time for any exhaled material to reach the receiver. Experiments show that t* ≈ 30 − 50 s for the jet to reach ℓ = 3 m [12], which matches the calculated result t* = 32 s using parameters in table II. The value of t* is usually much smaller than the critical time t separating the high- and low-risk regions in Fig. 4.
Space-time diagram of infection risks. The straight lines indicate N = Ninf, corresponding to the characteristic dose for infection (see equation 1). The infection risk is considered low (high) in the region below (above) the straight lines for each ϕ0. t* indicates the time for the jet to reach ℓ in the initial spreading stage. Below t* is the no-risk region. The plot is for a susceptible individual interacting with a single maskless asymptomatic speaker in a poorly ventilated space.
In all of above discussions an average virus concentration in saliva cυ = 7 × 106 mL−1 is assumed. However, for a superspreader, cυ = 2 × 109 mL−1, which is 300 times larger than the average value. Consequently, the time ts for N(ℓ, ts) = Ninf at ℓ = 3 m is ts ≈ 5 s (using 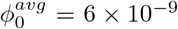 and other parameters listed in table II), which is much smaller than t* and means that the virion uptake by the receiver will surpass Ninf almost as soon as the jet reaches them. Therefore, the infection risk for speaking with a superspreader even for less than 1 min is high at a 3 m separation.
and other parameters listed in table II), which is much smaller than t* and means that the virion uptake by the receiver will surpass Ninf almost as soon as the jet reaches them. Therefore, the infection risk for speaking with a superspreader even for less than 1 min is high at a 3 m separation.
Wearing masks can block the formation of jet, filter droplets and aerosols and thus prevent the transmission of airborne virus; see review [30]. The filtration efficiency η varies with the type of the mask, particle size and flow velocities [31–34]. In theory, the droplet production rate while using a mask should be multiplied by a factor (1 − η), e.g., Ref. [35]. Experiments on droplets [33, 34] and flow [36, 37] filtered through a mask are usually conducted in the context of sneezing and coughing. The impacts of masks on the continuous speech-driven jets remains an open question to study.
III. CONCLUDING REMARKS
We analyzed the spatial and temporal dependence of local virus transmission during speaking by an asymptomatic individual in poorly ventilated environments and without masks. We used recent quantitative characteristics of speech [12] and properties of COVID-19 infected individuals. Both social distancing and decreasing contact time are important to keep the risk of infection low. This analysis suggests that the mask-free social distancing guidelines, 1 m according to WHO and 2 m according to CDC in the United States, should be accompanied by contact-time guidelines, which are ≈ 5 min for ℓ = 1 m and ≈ 15 min for ℓ = 2 m, in situations stated above and when the infected individual is not a superspreader. If the infected speaker is a superspreader, the infection risk is high within less than 1 min for ℓ = 3 m separation.
We also want to emphasize that the model presented here is for the worst-case scenario when the infected individual is actively speaking and the susceptible (maskless) individual is a passive listener. Future research is required for a better understanding of the more complex flow between two (or more) speakers and its impact on aerosol transmission.
Data Availability
All data are available and provided in the manuscript.
ACKNOWLEDGMENTS
We thank the National Science Foundation for support via the RAPID grant CBET 2029370 (Program Manager is Ron Joslin). We also thank the IRN “Physics of Living Systems” (CNRS/INSERM) for travel support for M.A.