Beyond Six Feet: A Guideline to Limit Indoor Airborne Transmission of COVID-19

The Well-Mixed Room

We first characterize the evolution of the pathogen concentration in a well-mixed room. We do so by adapting standard methods developed in chemical engineering to describe the ‘continuously stirred tank reactor’³⁵. We assume that the droplet-borne pathogen remains airborne for some time before either being extracted by the room’s ventilation system, inhaled or sedimenting out. The fate of ejected droplets is determined by the relative magnitudes of two speeds, the settling speed of the drop in quiescent air, υ_s, and the ambient air circulation speed within the room, υ_a. Drops of radius r ≤ 100μm and density ρ_d descend through air of density ρ_a and dynamic viscosity μ_a at the Stokes settling speed , prescribed by the balance between gravity and viscous drag, where g is the gravitational acceleration and Δρ = ρ_a−ρ_a. We consider a well-mixed room of area A, depth H and volume V = AH with ventilation outflow rate Q (as distinct from air recirculation rate) and air change rate (ACH) λ_a = Q/V. Equating the characteristic times of droplet settling, H/υ_s, and removal, V/Q, indicates a critical drop radius above which drops generally sediment out, and below which they remain largely suspended within the room prior to removal by ventilation outflow. We here define airborne transmission as that associated with droplets with radius r < r_c. The relevant physical picture, of particles settling from a well-mixed environment, is commonly invoked in the context of both stirred aerosols ³⁶ and sedimentation in geophysics³⁷. The additional effects of ventilation, particle dispersity and pathogen deactivation relevant in the context of airborne disease transmission were considered by Stiliankakis & Drossinos ¹³ and Buonanno et al.¹⁸, whose models will be built upon here.

It is noteworthy that, even in the absence of forced ventilation, there will generally be some mixing in an enclosed space: natural ventilation will lead to flows through windows or doors, and occupants will create additional air flow through their motion and respiration. Ventilation standards for American homes (ASHRAE 2016) recommend a minimal air exchange rate of λ_a = 0.35/h, a value comparable to the average of 0.34/h reported for Chinese apartments, including winter in Wuhan during the initial outbreak³⁸. Even with such minimal ventilation rates, for a room of height H = 2.1m there is an associated critical drop size of radius r_c = 1.3μm. The ‘airborne’ droplets of interest here, those of radius r < r_c, thus constitute a significant fraction of those emitted in most respiratory events^{9, 17, 25}. Moreover, a recent experimental study of the dependence of droplet size on the infectiousness of SARS-CoV-2 virions³ concluded that droplets with r > 2μm are less infectious, an inference that would underscore the importance of airborne transmission.

We consider a polydisperse suspension of exhaled droplets characterized by the number density n_d(r) (per volume of air) of drops of radius r and volume . The drop size distribution n_d(r) is known to vary strongly with respiratory activity and various physiological factors^9,18. The drops contain a microscopic pathogen concentration c_υ(r), a drop-size-dependent probability of finding individual virions ³, usually taken to be that in the sputum (RNA copies per mL) ¹⁸. The virions become deactivated (non-infectious) at a rate λ_υ(r) that may in principle depend on droplet radius or humidity ³⁹. However, since this dependence is not yet well characterized experimentally for SARS-CoV-2 in airborne droplets, we treat the deactivation rate as a constant bounded by existing estimates ¹⁹, λ_υ = 0 − 0.63/h. We note that deactivation rates may be enhanced by ultraviolet radiation (UV-C) ⁴⁰, chemical disinfectants (e.g. H₂O₂, O₃) ⁴¹, or high-efficiency particulate air (HEPA) filtration ⁴².

We seek to characterize the concentration C(r, t) of pathogen (per volume of air) transported by drops of radius r. We assume that each infectious individual exhales pathogen-laden droplets of radius r at a constant rate P(r) = Q_bn_d(r)V_d(r)p_m(r)c_v(r) (number/time), where Q_b is the breathing flow rate (exhaled volume per time). We introduce a mask penetration factor, 0 < p_m(r) < 1, that accounts for the ability of masks to filter droplets ^43,44. The concentration, C(r, t), of pathogen suspended within drops of radius r per infector then evolves according to where υ_s(r) is the particle settling speed. Owing to the dependence of the settling speed on particle radius, the population of each drop size evolves, according to equation (1), at different rates. Two limiting cases of Eq.1 are of interest. For the case of λ_υ = υ_s = 0, drops of infinitesimal size that do not deactivate, it reduces to the Wells-Riley model^{30, 31}. For the case of λ_υ = P = Q = 0, a non-reacting suspension with no ventilation, it corresponds to established models of sedimentation from a well-mixed ambient^{36, 37}. For the sake of notational simplicity, we define a size-dependent sedimentation rate λ_s(r) = υ_s(r)/H = λ_a(r/r_c)² as the inverse of the time taken for a drop of radius r to sediment from ceiling to floor in a quiescent room.

When one infected individual enters a room at time t = 0, the radius-resolved pathogen concentration increases as, C(r, t) = C_s(r) (1 − e^−λc(r)t), relaxing to a steady value, C_s(r) = P(r)/(λ_c(r)V), at a rate, λ_c(r) = λ_a + λ_s(r) + λ_υ. Note that both the equilibrium concentration and the timescale to approach it are decreased by the combined effects of ventilation, particle settling and deactivation ³⁹. Owing to the dependence of this adjustment process on the drop size, one may understand it as a dynamic sifting process wherein larger droplets settle out and reach their equilibrium concentration relatively quickly. However, we note that this adjustment time, , depends only weakly on drop size, varying from V/(2Q) for the largest airborne drops (with radius r_c) to V/Q for infinitesimal drops. The sedimentation rate of the ‘airborne’ droplets of radius r ≤ r_c is thus bounded above by the air exchange rate, λ_s(r) ≤ λ_a. The exhaled drop-size distribution depends strongly on respiratory activity ^{9, 18, 25, 45}; thus, so too must the radius-resolved concentration of airborne pathogen. The predicted dependence on respiratory activity ⁹ of the steady-state volume fraction of airborne droplets, ϕ_s(r) = C_s(r)/c_v(r) is illustrated in Fig. 1.

• Download figure
• Open in new tab

Figure 1:

Model predictions for the steady-state, droplet-radius-resolved aerosol volume fraction, ϕ_s(r), produced by a single infectious person in a well-mixed room. The model accounts for the effects of ventilation, pathogen deactivation and droplet settling for several different types of respiration in the absence of facemasks (p_m = 1). The ambient conditions are taken to be those of the Skagit Valley Chorale super-spreading incident^{19, 21} (H = 4.5m, A = 180m², λ_a = 0.65h⁻¹, λ_υ = 0.3h⁻¹, r_c = 2.6μm). The expiratory droplet size distributions are computed from the data of Morawska el al.⁹ (Fig. 3) for aerosol concentration per log-diameter, using n_d(r) = (dC/dlogD)/(r In 10). The breathing flow rate is assumed to be 0.5 m³/h for nose and mouth breathing, 0.75 m³/h for whispering and speaking, and 1.0 m³/h for singing.

We define the airborne disease transmission rate, β_a(t), as the mean number of transmissions per time between a given pair of infectious and susceptible individuals. One expects β_a(t) to be proportional to the quantity of pathogen exhaled by the infected person, and to that inhaled by the susceptible person. Gammaitoni and Nucci ¹⁰ defined the airborne transmission rate as β_a(t) = Q_bc_iC_s(t) for the case of a population evolving according to the Wells-Riley model and inhaling a monodisperse suspension. Here, c_i is the viral infectivity, the parameter that connects fluid physics to epidemiology, specifically the concentration of suspended pathogen to the infection rate. We note its relation to the notion of “infection quanta” in the epidemiological literature³⁰: c_i is the infection quanta per pathogen. The value of c has been inferred to lie in the range 0.01-0.1 for SARS-CoV ⁴⁶ and conjectured to be comparable for SARS-CoV-2 ¹⁸.

For the polydisperse suspension of interest here, we define the airborne transmission rate as thereby accounting for the protective properties of masks, and allowing for the possibility that the infectivity c_i(r) depends on droplet size. Different droplet sizes may emerge from, and penetrate into, different regions of the respiratory tract, and so have different c_i(r); moreover, virions on relatively small droplets may diffuse to surfaces more rapidly and so exchange with bodily fluids more effectively. Such a size dependence in infectivity, c_i(r), is also consistent with the recent experiments of Santarpia et al. ³, who reported that replication of SARS-CoV-2 is more apparent in droplets with radii r < 2.05μm, despite a nearly uniform viral load, c_υ(r), across all drop sizes.

Indoor Safety Guideline

The reproduction number of an epidemic, , is defined as the mean number of transmissions per infected individual. Provided , a disease will not spread at the population level ⁴⁷. Estimates of for COVID-19 have been used to compare its rate of spread in different regions and its dependence on different control strategies. ^48–50 We here define an analogous reproductive number for indoor, airborne transmission, , as the expected number of transmissions in a room of total occupancy N over a time τ from a single infected person entering at t = 0.

Our safety guideline sets a small tolerance e for the indoor reproductive number, defined as

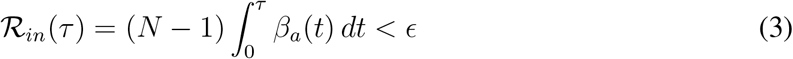
One may interpret as the probability of the first transmission, a probability that can be expressed as the sum of N − 1 independent transmission probabilities to each susceptible person in a well mixed room. As shown in the Supplementary Information, this guideline follows from standard epidemiological models, including the Wells-Riley model, in the ∊ ≪ 1 limit, but has broader generality. The exact transient safety bound, Eq. (3), appropriate for the time-dependent situation soon after the entrance of the infected index case, is evaluated in Methods.

We here focus on a simpler and more conservative guideline that follows for long times relative to the air residence time, (which may vary from minutes to hours), when the airborne pathogen has attained its equilibrium concentration C(r, t) → C_s(r). In this equilibrium case, the transmission rate (2) becomes constant: where, for the sake of simplicity, we assume constant mask filtration p_m over the entire range of aerosol drop sizes. We define the microscopic concentration of infection quanta per liquid volume as n_q(r) = n_d(r)V_d(r)c_υ(r)c_i(r), and the concentration of infection quanta or “infectiousness” of exhaled air, . The latter is the key disease-specific parameter in our model, which can also be expressed as the rate of quanta emission, λ_q = Q_bC_q, by an infected person. The second equality in Eq. (4) defines the effective radius of the settling drops (see Eq. (11) in Methods). The third equality defines the dilution factor, , the ratio of the concentration of infection quanta in the well-mixed room to that in the unfiltered breath of an infected person. As we shall see in what follows, this dilution factor provides a valuable diagnostic in assessing the relative risk of various forms of exposure.

We thus arrive at a simple guideline, appropriate for steady-state situations, that bounds the cumulative exposure time (CET):

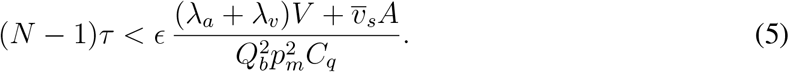
By noting that the sedimentation rate is effectively bounded by the air exchange rate, λ_s(r) < λ_a, and neglecting pathogen deactivation, we deduce from Eq. (5) a more conservative CET bound, the interpretation of which is immediately clear. To minimize risk of infection, one should avoid spending extended periods in highly populated areas. One is safer in rooms with large volume and high ventilation rates. One is at greater risk in rooms where people are exerting themselves in such a way as to increase their respiration rate and pathogen output, for example by exercising, singing or shouting. Since the rate of inhalation of contagion depends on the volume flux of both the exhalation of the infected individual and the inhalation of the susceptible person, the risk of infection increases as . Likewise, masks worn by both infected and susceptible persons will reduce the risk of transmission by a factor , a dramatic effect given that p_m ≤ 0.1 for typical masks ^{43, 44}.

Application to COVID-19

The only poorly constrained quantity in our guideline is the epidemiological parameter, C_q, the concentration of exhaled infection quanta by an infectious individual. While C_q is expected to vary widely between different populations ^51–53 and among individuals during progression of the disease ^{54, 55}, we proceed with a view to making rough estimates for C_q for different respiratory activities on the basis of existing epidemiological data. We do so with the hope that such an attempt will motivate the acquisition of more such data, and so to improved estimates for Cq in various settings.

An inference of C_q = 970 quanta/m³ was made by Miller et al. ¹⁹ in their recent analysis of the Skagit Valley Chorale super-spreading incident ²¹, on the basis of the assumption that the transmission was described in terms of the Wells-Riley model ^{10, 11, 18, 31}. This inference for C_q is roughly consistent with studies of other related viral diseases. For example, Liao et al.³² estimated Cq = 28 quanta/m³ from the rate of indoor spreading of SARS-CoV, in a hospital and an elementary school. Estimates of C_q for H1N1 influenza fall in the range 15 – 128 quanta/m^3,33. For SARS-CoV-2, Buonanno et al. ¹⁸ estimate a C_q range of 10.5-1030 quanta/m³, on the basis of the estimated infectivity c_i = 0.01 – 0.1 of SARS-CoV ⁴⁶ and the reported viral loads in sputum ^54–56, and note that the precise value depends strongly on the infected person’s respiratory activity. Notably, their range spans the high value inferred for the Skagit Valley Chorale ¹⁹, and all of our inferences to follow.

We proceed by estimating quanta emission rates Cq for different forms of respiration. First, we solve Eq. (1) to obtain the steady-state radius-resolved droplet volume fraction ϕ_s(r) for various hypothetical expiratory activities in the room of the Skagit Valley Chorale, using the drop size distributions of Morawska et al. ⁹. Our results are shown in Fig. 1. Integrating each curve up to the critical radius r_c, we then obtain an activity-dependent volume fraction of infectious airborne droplets in the choir room (see Supplementary Information). Finally, we assume that the inferred value, C_q = 970, for the super-spreading incident¹⁹ resulted from the expiratory activity most resembling singing (voiced “aahs” with pauses for recovery ⁹), and deduce values of C_q for other forms of respiration by rescaling with the appropriate ϕ₁ values. Our predictions for the dependence of C_q on respiratory activity are shown in Fig. 2. For validation, we also show estimates for C_q based on the recent measurements of activity-dependent aerosol concentrations reported by Asadi et al. ^25,45. Specifically, we calculated the aerosol volume fractions from the reported drop-size distributions (from Fig. 5 of Ref.⁴⁵) for a different set of expiratory activities that included various breathing patterns and speaking aloud at different volumes. We then used these volume fractions to rescale the value C_q = 72 quanta/m³ for speaking at intermediate volume ⁴⁵, which we chose to match the value inferred for the most similar respiratory activity considered by Morawska et al. ⁹, specifically voiced counting with pauses⁹. Notably, the quanta concentrations so inferred, C_q, are consistent across the full range of activities, from nasal breathing at rest (1-10 q/m³) to oral breathing and whispering (5-40 q/m³), to loud speaking and singing (100-1000 q/m³).

• Download figure
• Open in new tab

Figure 2:

Estimates of the COVID-19 “infectiousness” of exhaled air, C_q, defined as the concentration of infection quanta in the breath of an infected person, for various respiratory activities. Values are deduced from the drop-size distributions reported by Morawska el al. ⁹ (blue bars) and Asadi et al. ⁴⁵ (orange bars). The only value reported in the epidemiology literature, C_q = 970 quanta/m³, was estimated ¹⁹ for the Skagit Valley Chorale super-spreading event²¹. This value is rescaled by the predicted infectious aerosol volume fractions, , obtained by integrating the steady-state size distributions reported in Fig. 1 for different expiratory activities ⁹. Aerosol volume fractions calculated for various respiratory activities from Fig. 5 of Asadi et al. ⁴⁵ are rescaled so that the value C_q = 72 quanta/m³ for “intermediate” speaking matches that inferred from Morawska et al.’s ⁹ for “voiced counting”. Estimates of C_q for the outbreak during the quarantine period of the Diamond Princess and the initial outbreak in Wuhan City are also shown (see Supplementary Information for details).

Our inferences for C_q are also roughly consistent with physiological measurements of viral RNA in the bodily fluids of COVID-19 patients. Specifically, our estimate of C_q = 72 quanta/m³ for voiced counting ⁹ and intermediate-volume speech ⁴⁵ with integrated aerosol volume fractions ϕ₁ = 0.36 and 0.11 (μm/cm)³ corresponds, respectively, to microscopic concentrations of c_q = c_ic_υ = 2 × 10⁸ and 7 × 10⁸ quanta/mL (see Supplementary Information). Viral loads, c_υ, in sputum tend to peak in the range 10⁸ – 10¹¹ RNA copies/mL ^54–56, while much lower values have been reported for other bodily fluids ^{54, 55, 57}. Virus shedding in the pharynx remains high during the first week of symptoms and reaches 7 × 10⁸ RNA copies per throat swab ⁵⁴ (typically 1-3 mL). Since viral loads are 20-50% greater in sputum than in throat swabs⁵⁵, the most infectious aerosols are likely to contain c_υ ≈ 10⁹ RNA copies/mL. Using this value and the mean infectivity c_i = 2% reported for SARS-CoV ⁴⁶, Buonanno et al ¹⁸ inferred c_q = 2 × 10⁷ q/mL for SARS-CoV-2, an order of magnitude below our estimates obtained directly from spreading data for COVID-19. The inference that SARS-CoV-2 is ten times more infectious than SARS-CoV, with c_i > 10%, is consistent with the fact that only the former achieved pandemic status.

Our findings are consistent with emerging physiological³ and epidemiological^{5, 14, 17, 22} evidence that SARS-CoV-2 is present and extremely infectious in respiratory aerosols and that indoor airborne transmission may be the primary driver of the COVID-19 pandemic ^{4, 16}. Further support for this hypothesis is provided by crudely applying our indoor transmission model to the initial outbreak of COVID-19 in Wuhan ^{2, 48}. We assume that spreading occurred predominantly in family apartments, as is consistent with the inference that 80% of transmission clusters arose in homes ²³. We may then tentatively equate the average reproduction number estimated for the Wuhan out-break ⁴⁸, , with the indoor reproduction number, . We use τ = 5.5 days as the exposure time, assuming that it corresponds to mean time before the onset of symptoms and patient isolation. We consider the mean household size of 3.03 persons in a typical apartment with area 30 m²/person and a winter bedroom ventilation rate of 0.34 ACH ³⁸, and assume that λ_υ = 0.3/h and . We thus infer that C_q = 30 quanta/m³, which is consistent with the inference of Fig. 2 for normal breathing. As detailed in Supplementary Information, a comparable value can be inferred from a similar analysis of spreading of COVID-19 aboard the quarantined Diamond Princess cruise ship ²⁰, although that the extent to which the Diamond Princess can be adequately described in terms of a closed, well-mixed space remains the subject of some debate.

In summary, our inferences of C_q from a diverse set of indoor spreading events and from independent physiological data are sufficiently self-consistent to indicate that the values reported in Fig. 2 may prove to be sufficient to apply the safety guideline in a quantitative fashion. Our hope is that our attempts to infer C_q will motivate the collection of more such data from spreading events, which might then be used to refine our necessarily crude initial estimates.

Case studies and contact tracing

We proceed by illustrating the value of our guideline in estimating the maximum occupancy or exposure time in two settings of particular interest, the classroom and an elder care facility. Considering our inferences from the data and the existing literature, it would appear reasonable to illustrate our guideline for COVID-19 with the choice, C_q = 30 quanta/m³, bearing in mind that this value varies strongly with different demographics and respiratory activity levels ¹⁸. We thus assume that in both settings considered, occupants are engaged in relatively mild respiratory activities consistent with quiet speech or rest. In assessing critical cumulative exposure times for given populations, we stress that the tolerance ∊ is a parameter that should be chosen judiciously according to the vulnerability of the population, which varies dramatically with age and pre-existing conditions ^51–53.

We first apply our guideline to a typical classroom in the United States, designed for the standard occupancy of 19 students and their teacher (see Fig. 3(a)). The importance of adequate ventilation and mask use is made clear by our guideline. For normal occupancy and without masks, the expected time for the first transmission after an infected individual enters the classroom is 2.3 hours for natural ventilation and 18 hours with mechanical ventilation, according to the transient bound (12) with ∊ =1. These time limits are multiplied by in our safety guideline, and so would reach 23 to 180 hours with low-quality masks (p_m = 0.1) and a tolerance of ∊ = 0.1. Assuming six hours of indoor time per day, a school group wearing masks could thus meet for several days between the testing and subsequent removal of any newly infected individuals. With enhanced ventilation and judicious mask use, this time limit could be extended to several weeks, and so exceed the recovery time for COVID-19. We stress, however, that these predictions assume a “quiet classroom”, where resting respiration (C_q = 30) is the norm. Extended periods of physical activity, collective speech, or singing would lower the time limit by an order of magnitude (Fig. 2).

• Download figure
• Open in new tab

Figure 3:

The COVID-19 indoor safety guideline would limit the cumulative exposure time to lie beneath the curves shown. Evidently, the Six-Foot Rule becomes inadequate after a critical time, and the 15-Minute Rule above a critical occupancy, (a) Risk-adjusted occupancy, N_max/∊, versus mask-adjusted time, , spent indoors with an infected person. We choose typical values appropriate for a school classroom: 20 persons share a room with an area of 900 square feet and a ceiling height of 12 feet (A = 83.6 m², V = 301 m³). (b) Nursing home shared room with a maximum occupancy of three (A = 22.3 m², V = 53.5 m³), and a risk tolerance of ∊ = 0.01 chosen to reflect the vulnerability of the community. In both cases, curves deduced from the pseudo-steady formula, Eq. (5), are shown for both natural ventilation (λ_a = 0.34/h; blue curve) and mechanical ventilation (λ_a = 8.0/h; red curve). The transient formula (Eq.12 in Methods) is shown with dotted curves. System parameters are C_q = 30 quanta/m³, λ_υ = 0.3/h, Q_b = 0.5 m³/h, , . We stress that in (a), the maximum occupancy is normalized by the risk tolerance ∊, the occupancy time by the squared mask penetration factor, ; thus, the deduction of concrete numbers for maximum occupancy N_max for a given time, or maximum occupancy time 19 for a given N, requires an appropriate scale factor.

Our analysis sounds the alarm for elderly homes and long-term care facilities, which account for a large fraction of COVID-19 hospitalizations and deaths ^51–53. In nursing homes in New York City, law requires a maximum occupancy of three and recommends a mininum area of 80 square feet per person. In Fig. 3(b), we plot the guideline for a tolerance of ∊ = 0.01 transmission probability, chosen to reflect the vulnerability of the community. Once again, the effect of ventilation is striking. For natural ventilation (0.34 ACH), the Six Foot Rule fails after only 3 minutes under quasi-steady conditions, or after 17 minutes for the transient response to the arrival of an infected person, in which case the 15 Minute Rule is only marginally safe. With mechanical ventilation (at 8 ACH) in steady state, three occupants could safely remain in the room for no more than 18 minutes. This example provides insight into the devastating toll of the COVID-19 pandemic on the elderly ^{51, 53}. Furthermore, it underscores the need to minimize the sharing of indoor space, maintain adequate, once-through ventilation, and encourage the use of face masks.

In both examples, the benefit of face masks is immediately apparent, since the CET limit is enhanced by a factor , the inverse square of the mask penetration factor. Standard disposable surgical masks are characterized by p_m = 1 – 5% ⁴³, and so allow the cumulative exposure time to be extended by 400-10000 times. Even improvised cloth face coverings achieve p_m = 10 – 20% ⁴⁴, and so would extend recommended exposure times by a factor of 25-100. Our inference of the efficacy of face masks in mitigating airborne transmission is roughly consistent with studies showing the benefits of mask use on COVID-19 transmission at the scale of both cities and countries ^{16, 49}.

Finally, we illustrate the value of our guideline in contact tracing ⁵⁰, specifically, in prescribing the scope of the testing of people with whom an infected index case has had close contact. The CDC presently defines a COVID-19 “close contact” as any encounter in which an individual is within 6 feet of an infected person for at least 15 minutes. Figure 3 makes clear that this definition may grossly underestimate the number of individuals exposed to a substantial risk of airborne infection in indoor spaces. Our study suggests that whenever our CET bound (5) is violated during an indoor event involving the index case, one transmission is likely, with probability ∊. When the tolerance e exceeds a critical value, all occupants of the room should be considered close contacts and so warrant testing. For relatively short exposures (λ_aτ ≪ 1) initiated when the index case enters the room, the transient bound (12) should be considered.

For instructions on how to apply our guideline to other situations, we refer the interested reader to the spreadsheet provided in the Supplementary Information. There, by specifying a given room geometry, ventilation rate and respiratory activity, one may deduce the maximum cumulative exposure time in a particular indoor setting, and so define precisely what constitutes an exposure in that setting.

Beyond the Well-Mixed Room

The model developed herein describes the risk of small respiratory drops (r < r_c) in the case where the entirety of the room is well mixed. There are undoubtedly circumstances where there are substantial spatial and temporal variations of the pathogen concentration from the mean ^{7, 28}. For example, it is presumably the spatial variations from well-mixedness that result in the inho-mogeneous infection patterns reported for a number of well-documented transmission events in closed spaces, including a COVID outbreak in a Chinese restaurant ⁴, and SARS outbreaks on airliners ⁵⁸. In the vicinity of an infected person, the turbulent respiratory jet or plume will have a pathogen concentration that is substantially higher than the ambient^{15, 29}. Chen et al. ²⁸ referred to infection via respiratory plumes as ‘short-range airborne transmission’, and demonstrated that it poses a substantially greater risk than large-drop transmission.

On the basis of the relatively simple geometric form of turbulent jet and puff flows, one may make estimates of the form of the mixing that respiratory outflows induce, the spatial distribution of their pathogen concentration and so the resulting risk they pose to the room’s occupants. For the case of the turbulent jet associated with relatively continuous speaking or breathing, turbulent entrainment of the ambient air leads to the jet radius r = αx increasing linearly with distance x from the source, where α ~ 0.1 — 0.15 is the typical jet entrainment coefficient ^15,28,29. The conservation of momentum flux M = πρ_ar²υ² then indicates that the jet speed decreases with distance from the source according to υ(x) = M^1/2/(πρ_aαx). Concurrently, turbulent entrainment results in the pathogen concentration within the jet decreasing according to , where A_m ~ 2cm² denotes the cross-sectional area of the mouth and C₀ = C_q/c_υ is the exhaled pathogen concentration. Abkarian et al. ²⁹ thus deduce that for the respiratory jet generated by typical speaking, the concentration of pathogen is diminished to approximately 3% of its initial value at a distance of 2 meters.

In a well-mixed room, the mean concentration of pathogen produced by a single infected person is f_dC₀. For example, in the large, poorly ventilated room of the Skagit Valley Choir practice, we compute a dilution factor, of approximately 0.001. We note that since λ_c(r) > λ_a = Q/V, the dilution factor satisfies the bound, f_d ≤ Q_b/Q. For typical rooms and air exchange rates, f_d lies in the range of 0.0001 – 0.01. With the dilution factor of the well-mixed room and the dilution rate of respiratory jets, we may now assess the relative risk to a susceptible person of a close encounter (either episodic or prolonged) with an infected individual’s respiratory jet, and an exposure associated with sharing a room with an infected person for an extended period of time. Since the infected jet concentration C_j (x) decreases with distance from its source, one may assess its pathogen concentration relative to that of the well-mixed room, . There is thus a critical distance, beyond which the pathogen concentration in the jet is reduced to that of the ambient. This distance exceeds 10m for f_d in the aforementioned range and so is typically much greater than the characteristic room dimension. Thus, in the absence of masks, respiratory jets may pose a substantially greater risk than the well-mixed ambient.

We first consider a worst-case, close-contact scenario in which a person directly ingests a lung full of air exhaled by an infected person. An equivalent amount of pathogen would be inhaled from the ambient by anyone within the room after a time τ = V_b/(Q_bf_d), where V_b ≈ 500 mL is the volume per breath. For the geometry of the Skagit choir room, for which f_d = 0.001, the critical time beyond which airborne transmission is a greater risk than this worst-case close encounter with a respiratory plume is τ = 1.0 hour. We next consider the worst-case scenario governed by the 6-foot rule, in which a susceptible person is directly in the path of an infected turbulent jet at a distance of 6 feet, over which the jet is diluted by factor of 3% ²⁹. The associated concentration in the jet is still roughly 30 times higher than the steady-state concentration in the well-mixed ambient (when f_d = 0.001), and so would result in a commensurate amplification of the transmission probability. We note that our guideline could thus be adopted to safeguard against the risk of respiratory jets in a socially-distanced environment by reducing ∊ by a factor of C(6ft)/(f_dC₀), which is 3 - 300 for f_d in the range of 0.0001 - 001. We note that the latter worst-case scenario describes a static situation where a susceptible individual is seated directly in the respiratory plume of an infected individual, as may arise in a classroom or airplane ⁵⁸. More generally, with a circulating population in an indoor setting, one would expect to encounter an infected respiratory plume only for some small fraction of the time, consideration of which would allow for a less conservative choice of ∊.

Finally, we note that the use of face-masks will have a marked effect on respiratory jets, with the fluxes of both exhaled pathogen and momentum being reduced substantially at their source. Indeed, Chen et al. ²⁸ note that when masks are worn, the primary respiratory flow may be described in terms of a rising thermal plume, which is of significantly less risk to neighbours. With a population of individuals wearing face masks, the risk posed by respiratory jets will thus be largely eliminated, while that of the well-mixed ambient will remain.

Discussion and Caveats

We have focused here primarily on airborne transmission, for which infection arises through inhalation of a critical quantity of airborne pathogen, and neglected the roles of both contact and large-drop transmission ⁶. However, we note that the approach taken, coupling the droplet dynamics to the transmission dynamics, allows for a more complete description. For example, consideration of conservation of pathogen allows one to calculate the rate of pathogen sedimentation and associated surface contamination, consideration of which would allow for quantitative models of contact transmission and so inform cleaning protocols. A more comprehensive theory of the dynamics of disease transmission in enclosed spaces will be presented elsewhere.

Typical values for the parameters arising in our model are listed in Table 1 of the Supplementary Information. Respiration rates Q_b have been measured to be ~ 0.5m³/hr for normal breathing, and may increase by a factor of 3 for more strenuous activities ¹⁸. Other parameters, including room geometry (V, A and H = V/A) and ventilation rate will be room dependent. The most poorly constrained parameter appearing in our guideline is C_q, the concentration of pathogen in the breath of an infected person. However, using the value inferred for the Skagit Valley Chorale incident¹⁹, the best characterized super-spreading event, and rescaling using reported drop-size distributions^{9, 17, 25} has allowed us to estimate C_q for several respiratory activities, as listed in Figure 3. Further comparison with new inferences based on other super-spreading effects would allow for refinement of our estimates of C_q. As we expect such inferences to depend strongly on several factors, including the mean age of the population ⁵², one might also infer, in principle, how the infectivity depends on these factors. We thus appeal to the public health and epidemiology communities to document the physical conditions enumerated in Table 1 of the Supplementary Information for more indoor spreading events.

Adherence to the Six-Foot Rule would limit large-drop transmission, and to our guideline (5) would limit airborne transmission. We have also shown how the sizeable variations in pathogen concentration associated with near-field respiratory flows arising (in a population not wearing face-masks) might be taken into account, leading to a guideline that would bound both the distance between occupants and the cumulative exposure time. Circumstances may also arise, owing to the absence or deficiency of the air-conditioning or to irregularities in the room geometry and air circulation, where a room is only partially mixed. In the context of reducing COVID transmission in indoor spaces, such considerations need be made on a room-by-room basis. Nevertheless, the criterion (5) represents a minimal requirement for safety from airborne infection in well-mixed, indoor spaces.

We note further that we have neglected the influence of ambient humidity, which one expects to determine the rates of droplet shrinkage via evaporation or growth via condensation, and so influence the drop size distribution and ambient infectivity, C_q ^{8, 9, 28}. Moreover, we note that we have assumed that the global dynamics may be described in terms of a mean infectivity and susceptibility, while recent evidence suggests that there may be significant age-related variability in both^51–53. We emphasize that our inferences of C_q are all rooted in that inferred from the Skagit Valley Chorale super-spreading event¹⁹, where the median age was 69 ²¹; thus, the values reported in Fig. 2 are likely to represent conservative overestimates of C_q for younger, less vulnerable populations.

Our theoretical model of the well-mixed room was developed specifically to describe air-borne transmission between a fixed number of individuals in a single well-mixed room. Nevertheless, we note that it is likely to inform a broader class of transmission events. For example, there are situations where forced ventilation mixes air between rooms, in which case the compound room becomes effectively a well-mixed space. Examples considered here are the outbreaks on the Diamond Princess and in apartments in Wuhan City (see Supplementary Information); others would include prisons. There are many other settings, including classrooms and factories, where people come and go, in which case, they interact intermittently with the space, with infected people exhaling into it, and susceptible inhaling from it, for limited periods. This class of problems is also informed by our model provided one considers the mean population dynamics, specifically, that N be identified as the mean number of occupants.

Finally, the guideline (5) depends on the tolerance ∊, whose value in a particular setting should be set by the appropriate policy makers, informed by the latest epidemiological evidence. Nevertheless, this factor may be eliminated from consideration by using (6) to assess the relative behavioral risk posed to a particular individual by attending a specific event of duration τ with N other participants. We thus define a risk index, that may be evaluated using appropriate C_q and Q_b values listed in Figure 3. One’s risk increases linearly with the number of people in a room and duration of the event. Relative risk decreases for large, well ventilated rooms and increases when the room’s occupants are exerting themselves or speaking loudly. While these results are intuitive, the approach taken here provides a physical framework for understanding them quantitatively. It also provides a quantitative measure of the relative risk of certain environments, for example, a well ventilated, sparsely occupied laboratory and a poorly ventilated, crowded, noisy bar. Along similar lines, the weighted average of (7), provides a quantitative assessment of one’s risk of airborne infection over an extended period. It thus allows for a quantitative assessment of what constitutes an exposure, a valuable notion in defining the scope of contact tracing.

Above all, our study makes clear the inadequacy of the Six-Foot Rule in mitigating indoor airborne disease transmission, and offers a rational, physically-informed alternative for managing life in the time of COVID-19. If implemented, our safety guideline would impose a limit on the cumulative exposure time in indoor settings, violation of which constitutes an exposure for all of the room’s occupants. The spreadsheet included in the Supplementary Information provides a simple means of evaluating this limit for any particular indoor setting. Finally, our study indicates how new data on indoor spreading events may lead to improved estimates of the infectiousness of the disease and so to quantitative refinements of our safety guideline.

Methods

Competing Interests

The authors declare that they have no competing financial interests.