Model to Describe Fast Shutoff of CoVID-19 Pandemic Spread

Abstract

Early CoVID-19 growth obeys: 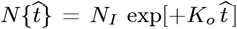, with K_o = [(ln 2)/(t_dbl)], where t_dbl is the pandemic growth doubling time. Given 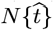, the daily number of new CoVID-19 cases is 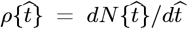. Implementing society-wide Social Distancing increases the t_dbl doubling time, and a linear function of time for t_dbl was used in our Initial Model: 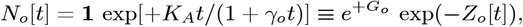to describe these changes, with G_o = [K_A/γ_o]. However, this equation could not easily model some quickly decreasing ρ[t] cases, indicating that a second Social Distancing process was involved. This second process is most evident in the initial CoVID-19 data from China, South Korea, and Italy. The Italy data is analyzed here in detail as representative of this second process. Modifying Z_o[t] to allow exponential cutoffs: 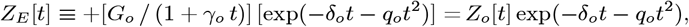provides a new Enhanced Initial Model (EIM), which significantly improves datafits, where 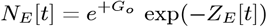. Since large variations are present in ρ_data [t], these models were generalized into an orthogonal function series, to provide additional data fitting parameters:

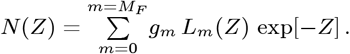
Its first term can give N_o[t] or N_E [t], for Z[t] → Z_o[t] or Z[t] → Z_e[t]. The L_m(Z) are Laguerre Polynomials, with L₀(Z) = 1, and {g_m; m = 0,M_F} are constants derived from each dataset. When ρ[t] = dN[t]/dt gradually decreases, using Z_o[t] provided good datafits at small M_F values, but was inadequate if ρ[t] decreased faster. For those cases, Z_E[t] was used in the above N(Z) series to give the most general Enhanced Orthogonal Function [EOF] model developed here. Even with M_F = 0, q_o = 0, this EOF model fit the Italy CoVID-19 data for ρ[t] = dN[t]/dt fairly well.

When the ρ[t] post-peak behavior is not Gaussian, then Z_E[t] with δ_o ≠ 0, q_o = 0; which we call Z_A[t], is also likely to be a sufficient extension of the Z_o[t] model. The EOF model also can model a gradually decreasing ρ[t] tail using small {δ_o, q_o} values [with 6 Figures].