Abstract
During a fast-moving epidemic, timely monitoring of case counts and other key indicators of disease spread is critical to an effective public policy response. We describe a nonparametric statistical method – originally applied to the reporting of AIDS cases in the 1980s – to estimate the distribution of reporting delays of confirmed COVID-19 cases in New York City. During June 21 – August 1, 2020, the estimated mean delay in reporting was 5 days, with 15 percent of cases reported after 10 or more days. Relying upon the estimated reporting-delay distribution, we project COVID-19 incidence during the most recent three weeks as if each case had instead been reported on the same day that the underlying diagnostic test had been performed. The statistical method described here overcomes the problem of reporting delays only at the population level. The method does not eliminate reporting delays at the individual level. That will require improvements in diagnostic technology, test availability, and specimen processing.
This study relies exclusively on publicly available, aggregate health data that contain no individual identifiers. The author has no competing interests and no funding sources to declare. This article represents to the sole opinion of its author and does not necessarily represent the opinions of the Massachusetts Institute of Technology, the National Bureau of Economic Research, Eisner Health, or any other organization.
Introduction
Timely surveillance of newly diagnosed cases is essential for effective control of the COVID-19 epidemic. When new infections are detected primarily through voluntary testing of symptomatic individuals, as is the case in the United States, there will be two main sources of delay in monitoring trends. First, there will be a testing delay between the actual date when an individual becomes infected and the date when that individual is ultimately tested. Second, unless test samples are very rapidly processed, there will be a further reporting delay between the date of testing and the date the test results are communicated by the reporting entity. The present research addresses the latter source of delay.
A statistical method for nonparametric or semiparametric estimation of the distribution of reporting delays was previous investigated in connection with delays in reporting of newly diagnosed AIDS cases during the 1980s (Harris 1990). The estimated distribution of delays allowed the analyst to predict the actual incidence of AIDS cases well before all cases were fully reported. That statistical method is adapted here to recent daily reports of newly diagnosed cases of COVID-19 by the New York City Department of Health and Mental Hygiene.
Data
All data were downloaded from the New York City health department repository (New York Department of Health and Mental Hygiene 2020b). The data consisted of a series of daily updates of a data file named case-hosp-death.csv. In this report, we relied solely on the first two variables in each updated file, labeled DATE_OF_INTEREST and CASE_COUNT, which we interpreted, respectively, as the date of diagnosis and the cumulative number of confirmed COVID-19 cases so far diagnosed by that date. We did not rely on data on hospitalizations or deaths in this study.
Methods
Statistical Analysis of Reporting Delays
From successive daily updates of the case-hosp-death.csv file, we computed the quantities ytu, corresponding to the number of confirmed infections diagnosed on date t but not reported until date t + u, that is, with a delay of u ≥ 0 days. For example, the version of the file case-hosp-death.csv showing all reports through 7/21/2020 indicated that 9 cases had been diagnosed on that date and thus far reported by that date. The following day’s version of case-hosp-death.csv indicated that a total of 65 cases had been diagnosed on 7/21/2020 and reported by 7/22/2020. Thus, we have yt 0 = 9 and yt1 = 65 − 9 = 56, where t corresponds in this example to the diagnosis date 7/21/2020. The very next day’s version indicated that a total of 132 cases had been diagnosed on 7/21/2020 and reported by 7/23/2020. Thus, we have yt 2 = 132 − 65 = 67. We used this method of successive differences to recover the underlying quantities ytu, which formed the basic data for our analysis.
Our statistical approach followed earlier work (Harris 1990). Let the possible dates of diagnosis t range from 0 to T, where T > 0 is the last date on which we have received case reports, which we’ll call the cutoff date. Let the duration of reporting delay u range from 0 to n, where n > 0 is assumed to be the longest possible reporting delay. We further assume that T > n > 0. As a result of this assumption, our sample is bifurcated into two parts, which we’ll call the early and late parts, respectively. The early part corresponds to dates of diagnosis t = 0,…,T − n. For these dates, we have by assumption a complete set {ytu, u = 0,1,…, n} of all reported cases diagnosed on each date. The late part corresponds to subsequent dates of diagnosis t = T − n + 1,…,T. For these dates, we have only a truncated set {ytu, u = 0,1,…,T − t} of reported cases diagnosed on each date, as some diagnoses have not yet been reported by the cutoff date T.
We considered the simplest model where the distribution of delays was independent of the date of diagnosis or any other observable, exogenous variable. That is, the probability that a case diagnosed at date t will be reported with delay u is αu, where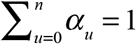 
. Let α = (α0, α1,…,αn) denote the vector of all parameters αu. Extensions of this basic model, including a variation in which 
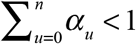, have been developed elsewhere (Harris 1990).
The basic idea is to estimate the delay distribution α from our observed data, and then use the estimate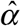 
to project the total number of cases diagnosed on a given date, including diagnoses yet to be reported. In general, we define 
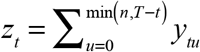as the total number of cases diagnosed on date t that have so far been reported by the cutoff date T. In the early part of the sample, for any date of diagnosis t = 0,…,T − n, this marginal sum simplifies to 
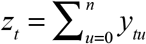and represents the total number of cases diagnosed on that date. So, conditional on the marginal sums zt, we have the projected number of cases ζt (α) = zt, which is independent of α. Since we have already observed all the cases diagnosed on date t, there is nothing unknown to project.
In the late part of the sample, for any date of diagnosis t = T − n + 1,…,T, we can instead write the marginal sums as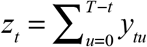 
. The projected number of cases diagnosed at date t will depend on the parameters as ζt (α)= zt/Ωt (α), where 
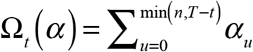is the estimated probability that a case diagnosed at date t will be reported by the cutoff date T.
We assume that the counts ytu are the realizations of independent Poisson random variables. Given the marginal sums zt, the conditional likelihood of the parameters α is maximized by the following iterative procedure, which is equivalent to the EM algorithm (Demster, Laird, and Rubin 1977). Let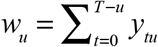 
denote the total number of cases reported with a delay of u days, summed over all dates of diagnosis t. We start with initial estimates 
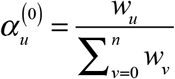for all u = 0,…, n. At iteration k = 0,1,2,… with provisional parameters α (k), we update our parameters to 
, where the denominator is the projected total number of diagnosed cases for which a delay u has been observed. To complete the iteration, we normalize to get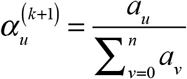 
. We continue to iterate until | α (k +1) − α (k)| is arbitrarily small.
Once we’ve converged on an estimate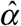 
, the projected case counts are 
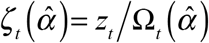for all t = 0,…,T.
Results
Distribution of Reporting Delays
Initial scanning of the data indicated that reporting delays have been increasing over the course of the epidemic since the initial outbreak in early March 2020. For cases diagnosed on or after June 21, however, the reporting distribution appeared to be stable with essentially all reports received within 21 days of diagnosis. We therefore designated June 21 as diagnosis date t = 0 and n = 21 days as the maximum reporting delay. As a result, the early part of our sample, that is, the range of dates t for which the observed case counts {ytu, u = 0,…,21} were complete, ran from June 21 through July 11. The late part of our sample, in which the observations on ytu were truncated, ran from July 12 through August 1, 2020.
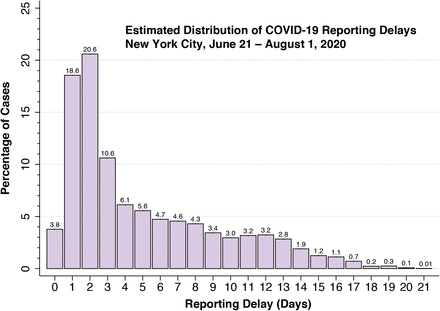
Figure 1 shows the estimated distribution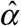 
of reporting delays. Only 3.8 percent of confirmed COVID-19 cases were reported on the same day that the underlying diagnostic test was performed, that is 
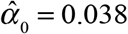. An additional 18.6 percent were reported on the following day, that is, 
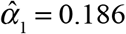, and another 20.6 percent were reported two days later, that is, 
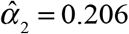. The mean reporting delay, based upon the assumption of full reporting by 21 days, was 4.96 days.
Figure 2 below shows the estimated cumulative distribution of reporting delays, that is, the cumulative percentage of diagnosed cases reported up to and including each delay interval. As indicated in the figure, an estimated 85.2 percent of diagnosed cases have been reported within 10 days from the date the underlying diagnostic test was performed.
Incidence of COVID-19 Cases Corrected for Reporting Delays
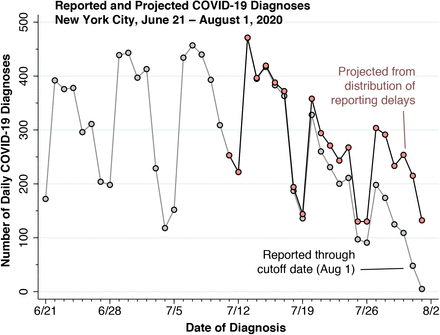
Figure 3 below shows the observed and projected counts of new daily COVID-19 cases from June 21 through August 1, 2020, the cutoff date of this study. Based only upon those cases reported through the cutoff date (gray data points), the number of cases appears to be heading downward. By contrast, the number of cases projected for the most recent 21 days once all delayed reports are received (pink data points) shows a different pattern. As of the August 1 cutoff date, the New York City health department had reported that zt = 198 cases were diagnosed on July 27. Based upon the estimated distribution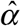 
in Figure 1, only the fraction 
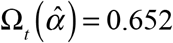of all cases should have been reported by that date. Hence, the projected number of cases actually diagnosed on July 27 would come to 
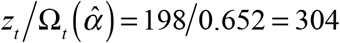. The information contained in the reporting-delay distribution thus serves to apprise decision makers that the most recent three weeks are not expected to show an unusual deviation from the previous trend in case reporting.
Neither the estimated distribution of reporting delays (Figures 1 and 2) nor the projected number of COVID-19 cases (Figure 3) varied significantly in response to changes in the June 21–August 1 observation interval or in the 21-day maximum duration of reporting delays.
Additional notes on the analysis of the data are given in Appendix 1.
Discussion
During a fast-moving epidemic, timely monitoring of case counts and other key indicators of disease spread is critical to an effective public policy response (Harris 2020b). The main objective of this article is to describe and test a statistical method for overcoming these delays, at least at the aggregate population level. The idea is to use recent past data on reporting delays in order to project the population-level counts of new cases as if they had all been reported on the date of diagnostic testing. The method does not eliminate reporting delays at the individual level – something that can be done only through improvements in diagnostic technology, test availability, and specimen processing.
Many state and local health departments – including the New York City health department – have tabulated counts of COVID-19 cases according to the date the relevant diagnostic test was performed. In contrast to tabulating cases according to the date the test result was received, this reporting convention has the advantage of assigning each case as closely as possible to the actual date of infection. The problem, however, is that the reporting agency has to continually update past counts every time a new case report is received. What’s worse, the most recent data points are invalid because all the cases haven’t yet come in (Harris 2020a). That is precisely what we see in the last two to three weeks of gray points in Figure 3.
The usual workaround for the delayed reporting problem is to attach an advisory that the most recent data are to be ignored. In fact, the data dashboard of the New York City department of health advises readers, “Due to delays in reporting, recent data are incomplete.” (New York Department of Health and Mental Hygiene 2020a) But this means that New York State’s so-called Early Warning Monitoring Dashboard actually tracks an incidence for New York City that is two to three weeks behind (New York State 2020).
A key message of this article is that, so long as the distribution of reporting delays is stable, the most recently reported case counts need not be ignored. The resulting timely estimate of recently diagnosed cases could have a significant impact on policy decisions to relax or tighten social distancing measures.
We estimated a mean delay of 5 days from the date of diagnostic testing to the date of a positive case report by the New York City health department. The cumulative reporting delay distribution in Figure 2 shows that even 10 days after diagnostic testing, about 15 percent of positive test results have yet to be reported. It is possible that individual patients are being informed of their positive test results before the data are entered into the health department’s aggregate public tally. Still, any significant delay in notification of positive test results at the individual level can have a critical adverse impact on the timing of a decision to self-quarantine. We have no data on the distribution of delays in reporting negative test results. Delays in notification of negative test results can similarly have adverse consequences for the timing of an individual decision to continue working or to return to work.
Even with the proposed statistical correction for reporting delay, there remains the problem of testing delay. In the system of voluntary, symptom-motivated testing in the United States, testing delay has two components. The first is the incubation period between initial infection and first symptoms of illness, estimated to be about 5.1 days (Lauer et al. 2020). The second is the additional delay between the onset of symptoms and date the test is performed. In a voluntary system, testing delays can be reduced by patient education, enhanced availability of walk-in and drive-through testing. Alternative testing technologies that would permit rapid, self-testing would go far to reduce these critical bottlenecks (Larremore et al. 2020).
The statistical method proposed here assumes that reports arrive according to an independent, homogeneous Poisson process. Reporting delays could vary according to laboratory of diagnosis, duration or severity of infection, and characteristics of the individual patient.
Reports could also arrive in batches. Data to test these possibilities are currently unavailable. While virtually all reports since June 21 were received within 3 weeks, there remains the possibility that reporting delays will further increase. If so, correction for delays will assume even greater importance for timely detection of epidemic trends.
As shown in Figure 3, the incidence of new confirmed COVID-19 cases in New York City has continued to remain stable at under 500 cases per day. This observed flattening of the incidence curve may reflect a delicate balancing between falling and rising incidence in different demographic or geographic groups, and thus may not remain stable. Further monitoring of newly diagnosed cases, aided by information from the reporting delay distribution as described here, will permit timely determination as to whether this apparent stability is persistent or fleeting.
Data Availability
Links to the underlying data sources are contained in the references. The author will make all other data and calculations available.
Appendix 1. Additional Notes on Data Analysis
The New York City department of health did not post a case-hosp-death.csv file for cases reported through June 28. The corresponding observations on ytu were therefore imputed from the following day’s case-hosp-death.csv file and the estimated reporting delay distribution through June 27. In addition, in scattered instances, the computed value of ytu was negative, presumably due to correction of prior reporting errors. In those cases, we distributed the reduction uniformly across prior case counts for the same date of diagnosis {ytv, v = 0,…,u − 1}, setting ytu = 0.
