Abstract
In this paper, we compare the inference regarding the effectiveness of the various non-pharmaceutical interventions (NPIs) for COVID-19 obtained from two SIR models, both produced by the Imperial College COVID-19 Response Team. One model was applied to European countries and published in Nature 1, concluding that complete lockdown was by far the most effective measure and 3 million deaths were avoided in the examined countries. The Imperial College team applied a different model to the USA states 2. Here, we show that inference is not robust to model specification and indeed changes substantially with the model used for the evolution of the time-varying reproduction number, denoted by Rt. Applying to European countries the model that the Imperial College team used for the USA states shows that complete lockdown has no or little effect, since it was introduced typically at a point when Rt was already very low. We also show that results are not robust to the inclusion of additional follow-up data.
1 A Tale of Two Models
The two models (Flaxman et al.1 and Unwin et al.2) produced by the Imperial College COVID-19 Response Team aim to explain the evolution of Rt. We will refer to these models as model 1 (the model applied to European countries in the Nature publication1) and model 2 (the model applied to the USA states2), respectively. The two models for the Rt are fundamentally different. In model 1, the proportional variation of Rt from the initial R0 is modelled as a step function and only allowed to change in response to an intervention. Therefore, any decrease in Rt (even if this decrease is a result of the increasing proportion of the population who are infected, to changes in human behaviour, clustered contact structures and/or pre-existing immunity3) must, by the model construction, be attributed to interventions and the impact is immediate with no time lag or gradual change, when a new intervention is adopted. In model 2, the proportional variation of Rt from R0 has a different functional form and is allowed to vary with mobility indicators for various activities. These mobility indicators are proxies for changes in human behaviour, whether that change is due to one or more centrally imposed interventions or whether it is the product of individuals responding to the epidemic on their own initiative independently of centrally imposed interventions. Model 2 also does not presume step functions and is therefore capable of capturing more gradual changes over time. Model 1 is deliberately simple and designed to test the impact of interventions without the confounders of mobility data, which themselves could be the product of the interventions. Model 2 leaves out interventions and uses mobility data as predictors in the evolution of Rt. The advantage of model 2 is that it gives a more flexible estimate of Rt, by allowing it to change with mobility trends. Although there is no explicit causal structure in model 2, the time sequence of the data and events makes inference around the impact of interventions possible by observing if the change in Rt precedes a given intervention or interventions or not. Here, we apply both models 1 and 2 to the European data to compare the results and inferences they obtain. See supplementary methods for details on methods and data.
2 Results
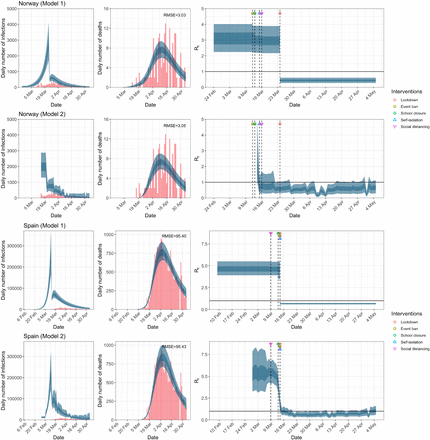
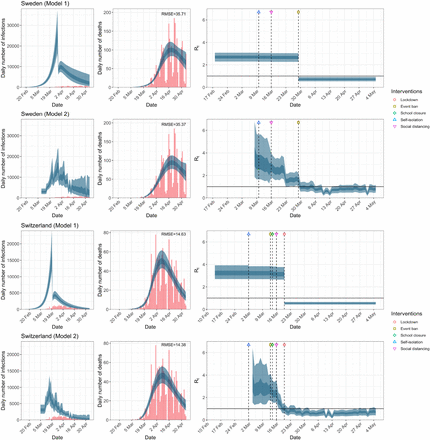
There are two main observations when comparing the modeling results in Figure 1a, as well as the corresponding Extended Data Figures 1a–1e. First, and most notable, is that while the models give very different trajectories of Rt, both models produce similar and accurate fit to the observed daily death counts. That is, very different processes of Rt give rise to the same daily death count data. The second observation is that inference regarding the impact of interventions varies significantly between the two models. The inference from model 1 indicates that lockdown had the biggest impact of all the interventions in all countries. Indeed, Flaxman et al.1 states that Lockdown has an identifiable large impact on transmission (81% [75%-87%] reduction).
Austria and Belgium. Plots of daily infections, daily deaths and time-varying reproduction number Rt until May 5th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Denmark and France. Plots of daily infections, daily deaths and time-varying reproduction number Rt until May 5th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Germany and Italy. Plots of daily infections, daily deaths and time-varying reproduction number Rt until May 5th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Norway and Spain. Plots of daily infections, daily deaths and time-varying reproduction number Rt until May 5th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Sweden and Switzerland. Plots of daily infections, daily deaths and time-varying reproduction number Rt until May 5th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
United Kingdom. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
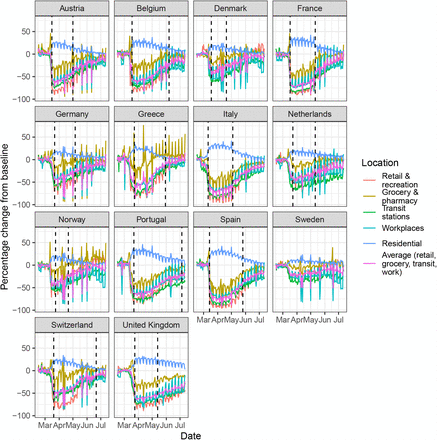
In contrast, model 2 shows clearly that Rt was falling well before lockdown, which occurred after the sharp decline in Rt. With the exception of Belgium (and to a lesser degree France), this is consistently seen across the European countries (see Extended Data Figures 1a–1e) and is in line with the mobility data, see Figure 2. At the time lockdown was adopted in the UK, Rt had already decreased to 1.46 (95% CI, 0.89 to 2.20) from an initial R0 of 4.46 (95% CI, 2.62 to 7.20) according to model 2, and the largest drop in Rt occurred after the implementation of self-isolation measures and encouraging social distancing, see Table 1.
Basic reproduction number R0 and time-varying reproduction number Rt immediately at time of introduction of NPIs given by both models using data up to May 5th for all eleven countries analysed in Flaxman et al.1. These NPIs are self-isolation (SI), social distancing (SD), school closure (SC), event ban (EB) and lockdown (LD). 95% credible intervals are given in parentheses below the corresponding point estimates. Countries where the seeding of new infections occur after the introduction of NPIs are denoted with an asterisk.
Percentage change in mobility from baseline level from February 15th to July 12th, by locations in each of the European countries examined in Flaxman et al. 1, as well as an additional three countries consisting of Greece, the Netherlands and Portugal. Average mobility is computed based on the trends in retailers and recreation venues, grocery markets and pharmacy, transit stations and workplaces. Black dashed lines in each plot indicate the lockdown start and end dates.
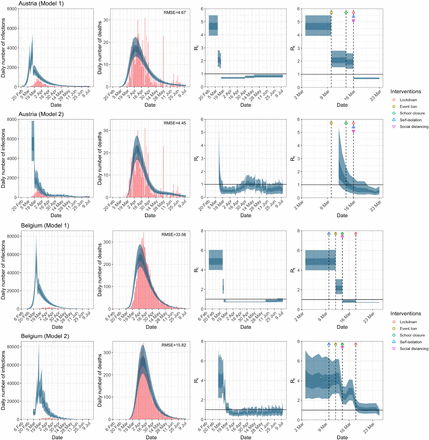
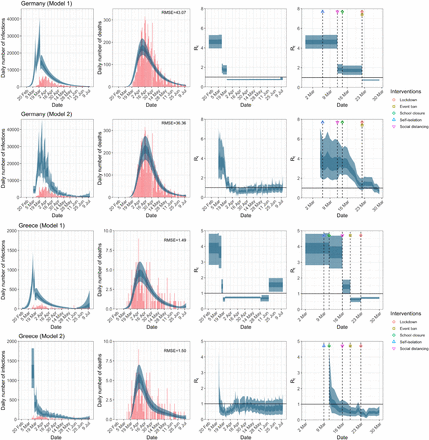
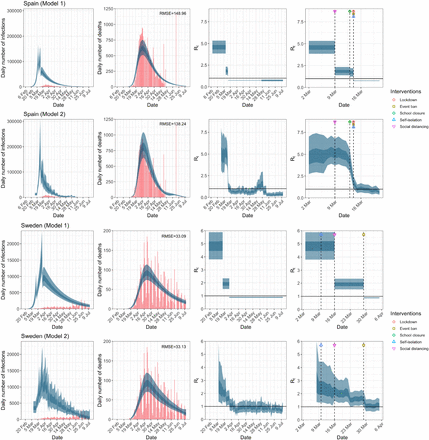
We also evaluated the effect of extending the time horizon of analysis until July 12th where restrictions had been lifted in some of these countries. We include an additional three countries, i.e. Greece, the Netherlands and Portugal, in the analysis. Extended Data Table 1 shows the end dates of school closures, ban on public events and lockdown used in the analysis. Figure 1b shows a comparison of the results obtained from both models for the UK for the extended data while Extended Data Figures 2a–2g show similar results for the remaining 13 countries. Table 2 tabulates the original R0 and Rt at the time of adoption of each NPI in each country for both models for the period March 4th to July 12th. The change in inference from model 1 as a result of the additional data is astonishing. Table 2, Figure 1b, and Extended Data Figures 2a–2g show that with the inclusion of the data until July 12th, Rt before lockdown was already below 1 for ten of the fourteen countries. The 95% credible intervals for the UK, Austria, Germany and Spain exceeded 1 before lockdown. Indeed, in contrast to the results reported in the Nature paper1, results from model 1 suggest that the banning of public events and social distancing are more proximally related to the reduction in Rt than lockdown. For example, while the results from model 1 in Figure 1a, which corresponds to the data until May 5th, suggests that lockdown led to the largest decrease in Rt, it now indicates that the largest decrease in Rt happened after social distancing is practised from a mean value of 5.27 (95% CI, 4.50 to 6.04) to 2.10 (95% CI, 1.61 to 2.64)! Note that the inference from model 1 regarding the relative effectiveness of lockdown is now more consistent with the inference from model 2 across most countries. Finally, we should point out that Figure 1b show that the gradual increase in Rt following the minimum value commenced well before the lifting of lockdown. This suggests that as people become less frightened by the prospect of a catastrophe, mobility (see Figure 2), and hence the time-varying reproduction number increases.
Austria and Belgium. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Denmark and France. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Germany and Greece. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Italy and the Netherlands. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Norway and Portugal. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Spain and Sweden. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Switzerland. Plots of daily infections, daily deaths and time-varying reproduction number Rt in columns 1–3 until July 12th. The start time for the plots is 30 and 10 days before 10 deaths are recorded, in the two models, respectively. Column 4 is a magnification of column 3 around the period of the NPIs. Observed counts of daily infections and daily deaths are shown in red, and their corresponding 50% and 95% CIs are shown in dark blue and light blue respectively.
Basic reproduction number R0 and time-varying reproduction number Rt immediately at time of introduction of NPIs given by both models using data up to July 12th for all eleven countries analysed in Flaxman et al.1 plus Greece, the Netherlands and Portugal. These NPIs are self-isolation (SI), social distancing (SD), school closure (SC), event ban (EB) and lockdown (LD). 95% credible intervals are given in parentheses below the corresponding point estimates. Countries where the seeding of new infections occur after the introduction of NPIs are denoted with an asterisk.
3 Conclusion
These findings clearly present policy makers with a conundrum. Which results should be used to guide policy making in lifting restrictions? Flaxman et al.1 make the statement We find that, across 11 countries, since the beginning of the epidemic, 3,100,000 [2,800,000 - 3,500,000] deaths have been averted due to interventions. However, we have shown that two different models, both of which give plausible fits to the actual death count data, yield vastly different inferences concerning the effectiveness of intervention strategies for the period March 4th to May 5th in the UK. Results are also different when the observation period is extended and easing of restrictions is included in the model. Although it is tempting to congratulate ourselves on our decision to implement lockdown, citing the number of lives that were saved, we should resist this temptation, and examine other possible explanations. Failure to do this and therefore mis-attribute causation could mean we fail to find the optimal solution to this very challenging and complex problem, given that complete lockdown can also have many adverse consequences4.
We do not want to reach the opposite extreme of claiming with certainty that lockdown definitely had no impact. Other investigators using a different analytical approach have suggested also benefits from lockdown, but of much smaller magnitude (13% relative risk reduction5) that might not necessarily match complete lockdown-induced harms in a careful decision analysis. Another modeling approach has found that benefits can be reaped by simple self-imposed interventions such as washing hands, wearing masks, and some social distancing6. Observational data need to be dissected very carefully and substantial uncertainty may remain even with the best modelling7. Regardless, causal interpretations from models that are not robust should be avoided. Given the analyses that we have performed using the two models that the Imperial College team has developed, one cannot exclude that the attribution of benefit to complete lockdown is a modelling artefact.
Author Contributions
All authors contributed equally to this work. VC performed all the computations and produced all the graphics. SC wrote the initial draft. JI and MT wrote subsequent drafts. All authors discussed the results and implications and commented on the manuscript at all stages.
Conflicts of Interest
None.
Code Availability
All source code for the replication of our results is available from the Imperial College COVID-19 Response Team’s Github repository: https://github.com/ImperialCollegeLondon/covid19model. Daily confirmed cases and deaths data are publicly available from the European Centre of Disease Control’s website.
Supplementary Methods
Model 2 assumes that Rt is a function of mobility and allows this impact to vary regionally by the use of regional specific random effects terms. The data used by Unwin et al.2 to estimate Rt is the Google’s COVID-19 Community Mobility Report. We adapt this methodology to the European context by modelling potential idiosyncrasies in mobility trends across countries using country-specific random effects. To complete the specification of model 2 for the European data, we use Google’s COVID-19 Community Mobility Report8 which provides data measuring the percentage change in mobility compared to a baseline level for visits to a number of location categories; retailers and recreation venues, grocery markets and pharmacies, parks, transit stations, workplaces and residential places. We use the average change in mobility across all location categories, excluding residential places and parks, as a measure of the reduction in mobility.
The seeding of new infections in model 2 is chosen to be 10 days before the day a country has cumulatively observed 10 deaths so that mobility data are available for all the countries examined. In the UK, this corresponds to March 4th, which is later than the infection start date of February 13th used by Flaxman et al. 1.
For posterior inference of model 2, we use the same prior distributions as in Unwin et al.2 except for R0, where a weakly informative prior of a normal distribution truncated below at 1 with mean 3.28 and standard deviation 2 is used. This prior is chosen so that approximately 95% of the prior density is between 1 and 79, and that R0 is above the critical value of 1 at the start of the epidemic. For model 1, we use the same priors as in Flaxman et al. 1 for the analysis up to May 5th and July 12th.
Acknowledgement
We congratulate the Imperial College Response Team for sharing openly the code for their models and for the overall transparency of their work that has allowed performing these analyses. We also thank Jack Wood for his help in the construction of Extended Data Table 1.