Abstract
As SARS-CoV-2 continues to spread around the world while the pandemic lasts, testing facilities are forced to massively increment their testing capacities to handle the increasing number of samples. While sample pooling methods have been proposed or are effectively implemented in some labs, no systematic and large-scale simulations have been performed using real-life quantitative data from testing facilities. Here, we use anonymous data from 1632 positive cases to simulate and compare 1D and 2D pooling strategies. We show that the choice of pooling method and pool size is an intricate decision with a prevalence-dependent efficiency-sensitivity trade-off.
Introduction
Massive screening of the population for SARS-CoV-2 infection is proposed as one of the key strategies in the global battle against the COVID-19 pandemic. Due to the immense number of samples that are analyzed during population screening, pooling of samples seems to be a valid strategy in overcoming shortages in reagents and increasing testing capacity.
Several pooling strategies in the frame of SARS-CoV-2 testing have been discussed in recent preprints. The most discussed method is referred to as one-time pooling1–4. In this strategy, the samples are pooled, pools are tested and only samples in positive pools are tested individually. A second popular approach is called sequential pooling1,5 in which the samples are pooled, pools are tested and positive pools are split into two equally-sized sub-pools. These sub-pools are tested again and this process is repeated until the individual sample level is reached. The third method that has been explored is two-dimensional or 2D pooling6. This method organizes samples in a 2D matrix and then creates pools along the rows and columns of the matrix. The pools are tested and negative rows and columns are excluded from the matrix. Next, all remaining samples are tested individually. Finally, researchers have explored pooling strategies in which samples are assigned to multiple pools, but require only one round of testing. Given the composition and test results of the positive pools, the positive samples can immediately be identified without the need for further individual testing. P-BEST7 and Tapestry8 are examples of such strategies.
While attractive, pooling strategies come with inherent limitations. First, pooling dilutes each individual sample, possibly to such an extent that the viral RNA becomes undetectable, resulting in false negative observations9–11. A second limitation is that an increase in sample manipulations augments the risk of cross-contamination and sample mix-ups, which can lead to false negatives and false positives6. Other drawbacks are unique to specific strategies. The P-BEST pooling protocol is very time consuming, even when using a pipetting robot7. The repeated pooling method, on the other hand, suffers from a complicated re-pooling scheme1.
Although the number of preprints and peer-reviewed publications on pooling strategies for COVID-19 PCR-based testing has increased rapidly throughout the pandemic, some important insights are still lacking. First of all, the proposed optimal pooling strategy is often based on a binary classification of samples as either positive or negative. However, this Boolean approach is not in accordance with the real-world situation and does not allow for investigating the dilution effect of pooling. Second, when using a quantitative representation of the viral loads, these values need to reflect real-life data, as patients present a very wide range of viral loads. This is reflected in the wide spectrum of Cq values reported by PCR-based tests12. Finally, as pooling is most effective for population-wide screening (where a very low prevalence is expected) it is important to determine the performance of strategies when encountering a low fraction of positive samples.
Here, we evaluate one-time (or 1D) pooling and two-dimensional (2D) pooling (using practical microtiter plate format pool sizes) as promising strategies for massive, low-prevalence population screening using real-life RT-qPCR data from 1632 positive samples.
Results
Inverse relationship between efficiency and prevalence
In order to evaluate the efficiency-gain of the adopted pooling strategies, we calculated the number of tests that are needed to analyze all samples and divided this number by the total number of samples. We calculated the median, minimum and maximum prevalence-specific efficiency for each pooling strategy (Figure 1). First, we observe an inverse relationship between efficiency and prevalence over the evaluated prevalence range from 0.01% to 10% for all pooling strategies. Second, there is no single most efficient strategy, because this depends on the prevalence (notice crossings in Figure 1). Until a prevalence of 0.36%, 1×24 is the most efficient strategy, from 0.40% to 2.51% 16×24 becomes the most efficient, from 2.82% to 4.47% the most efficient strategy is 12×24 and from 5.01% to 10% 8×12 is the most efficient strategy. However, at high prevalence all strategies show similar efficiency gain. Third, strategies employing a larger pool size display a higher efficiency when the prevalence is low, but as the prevalence increases, there is a tipping point for each strategy at which its smaller pool size variant becomes more efficient. At very low prevalence, the efficiency of a 1 x n pool size becomes n and that of a m x n pool strategy becomes (m x n) / (m + n). As a general trend, 2D pooling methods are less sensitive to changes in prevalence in comparison with 1D pooling methods. We conclude that the most efficient pool size very much depends on the prevalence, but 2D pooling methods generally are most efficient when prevalence is higher than 0.4%.
Average efficiency increase (number of samples divided by the number of tests performed) over a 0.01 to 10% prevalence range for different pooling strategies. The averages are approximated by the median over five replicate simulations of a cohort size of 100 000 patients each. The ranges around the line indicate the minimum and maximum value over five replicate simulations.
Sensitivity decreases with lower prevalence
The true performance of a pooling strategy cannot be evaluated by efficiency only. Since the number of false negatives due to pooling is one of the main possible drawbacks of sample pooling, it is necessary to take this into account when choosing the optimal strategy. In this regard, we calculated the average sensitivity of the different simulated settings (Figure 2, Supplemental Figure 3), which ranges from 0.636 to 0.968. For all of the pooling strategies—and irrespective of pool size—we primarily see that sensitivity increases with increasing prevalence. There is a non-linear relationship between sensitivity and prevalence. Furthermore, since prevalence is linked with efficiency and as a result indirectly linked with sensitivity, we note that an increase in efficiency comes with a decrease in sensitivity. We also observe that at a prevalence lower than 1%, there is an increased variation in sensitivity for different simulation cohorts. Thus, the increased efficiency at low prevalence comes with a low and pool size-dependent problematically variable sensitivity.
Sensitivity in function of the prevalence for different strategies. Each point is colored by its corresponding efficiency. Each data point illustrates the median value of five replicate simulations, each simulation starting from a set prevalence and pooling strategy for a testing cohort of 100 000 patients.
Sensitivity loss in function of viral load
With the intention of determining the influence of the viral load and, as a proxy, Cq value of the positive sample on the sensitivity associated with the pooling strategies, we calculated the probabilities of a true-positive for each non-pooled original Cq value (Supplemental Figure 2). We investigated how the sensitivity changes when higher Cq values are progressively being included in the cohort, starting with samples with highest viral load (lowest Cq value) (Figure 3, Supplemental Figure 4). In the first place, we note that the Cq value at which sensitivity loss starts to occur only depends on the 1D pool size or largest dimension of the 2D pool; i.e. Cq value of 35 for 1×4, 34 for 1×8, 33.4 for 1×12 and 8×12, 33 for 1×16 and 12×16 and 32.4 for 1×24 and 16×24. These Cq values are (as expected) identical to 37 − log2(largest pool size). Additionally, when Cq values larger than these cut-off values are systematically included, the sensitivity drops exponentially. The rate at which this reduction happens, decreases when prevalence increases. Finally, when the prevalence is 10%, larger pool sizes result in a smaller reduction in sensitivity, but for all other visualized prevalence values the sensitivity decreases with larger pool size. Altogether, the extent to which low viral load samples contribute to the drop in sensitivity depends on pool size and pooling strategy, although the sensitivity decrease is most problematic when prevalence is low.
Cumulative sensitivities calculated for all Cq values up to a cut-off Cq for four prevalences. All true positives and false negatives over five replicate simulations for each sampled Cq value are counted and used for calculation of the sensitivity up to the cut-off Cq. The data is filtered for prevalences of 0.01%, 0.1%, 1% and 10% and grouped by prevalence.
Discussion
Sample pooling strategies form an incredible asset in an attempt to increase throughput in times when massive testing for COVID-19 would be needed. A plethora of pooling strategies have been suggested, some more performant or practical than others. 1D and 2D pooling methods were selected in this simulation study because they are simple and quick to perform, have straightforward pipetting schemes and do not require re-accessing the same sample more than twice. Pool sizes were selected to be easily compatible with 96-well plates. Using a large real-life dataset of 1632 positive samples enabled us to simulate relevant settings and provide more accurate outcomes in comparison with real wet-lab tests, which are rather limited in the number of positive samples and may not cover the whole range of viral loads. Because the original Cq distribution depends on the origin of the sample (hospital, care center,…) and the stage of pandemic, our observations do as well. Firstly, our results confirm the widely accepted idea that sample pooling methods show a higher efficiency when prevalence is low1–6,13 and that, for 1D and 2D pooling methods, as prevalence increases, a threshold is reached after which smaller pool sizes become more efficient1,6. However, appraising the performance of a pooling method exclusively by its efficiency would ignore one of the major drawbacks of pooling: loss of sensitivity due to dilution of the target. This issue becomes most pertinent when the viral load is low9–11,13,14. Our results confirm that all tested pooling methods suffer from false negatives, to a variable degree (Figure 2). This loss in sensitivity across all prevalence conditions generally precludes use of pooling for diagnostic testing of COVID-19 samples according to the U.S. Food and Drug Administration (FDA), whereby only 1×16 and 1×24 strategies under high prevalence (≥10%) conditions meet the minimal 95% sensitivity requirement15. When prevalence is high, the loss in sensitivity for large pools is partly compensated by the fact that low viral load samples can be ‘rescued’ by high viral load samples when present in the same pool. (Figure 3). Intuitively, 2D pooling methods are especially vulnerable for false negatives, as a high Cq sample would have to be ‘rescued’ in the corresponding row and column pools, which is confirmed by our results. The influential role of prevalence on efficiency as well as sensitivity presents an import challenge, considering that, in order to make an informed decision on the preferential pooling strategy, the prevalence has to be known. By nature, we cannot know the exact prevalence before testing our samples, and as a result, the prevalence has to be estimated. In general, we show that it is of extreme importance that an optimal equilibrium between efficiency and sensitivity is achieved when deciding on the pooling strategy and corresponding pool size.
Materials and Methods
Patient samples
Nasopharyngeal swabs were taken by a healthcare professional as a diagnostic test for SARS-CoV-2, as part of the Belgian national testing platform. The individuals were tested at nursing homes or in triage centers, between April 9th and June 7th. To mimic low prevalence viral loads as much as possible, only batches of 94 patient samples with fewer than 10 positives were included in this study. After additional filtering as described in a further paragraph, this resulted in 113 928 patients in total, of which 1632 positives (1.43%) with corrected Cq values ranging from 9.85 to 36.94 (median of 28.78) (Supplemental Figure 1).
SARS-CoV-2 RT-qPCR test
RNA extraction was performed using the Total RNA Purification Kit (Norgen Biotek #24300) according to the manufacturer’s instructions using 200 μl transport medium, 200 μl lysis buffer and 200 μl ethanol, with processing using a centrifuge (5810R with rotor A-4-81, both from Eppendorf). RNA was eluted from the plates using 50 μl elution buffer (nuclease-free water), resulting in approximately 45 μl eluate. RNA extractions were simultaneously performed for 94 patient samples and 2 negative controls (nuclease-free water). After addition of the lysis buffer, 4 μl of a proprietary 700 nucleotides spike-in control RNA (40 000 copies) and carrier RNA (200 ng of yeast tRNA (Roche #10109517001) was added to all 96 wells from the plate). To the eluate of one of the negative control wells, 7500 RNA copies of positive control RNA (Synthetic SARS-CoV-2 RNA Control 2, Twist Biosciences #102024) were added. Six μl of RNA eluate was used as input for a 20 μl RT-qPCR reaction in a CFX384 qPCR instrument using 10 μl iTaq one-step RT-qPCR mastermix (Bio-Rad #1725141) according to the manufacturer’s instructions, using 250 nM final concentration of primers and 400 nM of hydrolysis probe. Primers and probes were synthesized by Integrated DNA Technologies using clean-room GMP production. For detection of the SARS-CoV-2 virus, the Charite E gene assay was used (FAM)16; for the internal control, a proprietary hydrolysis probe assay (HEX) was used. Prior to May 25th, 2 singleplex assays were performed; after May 25th, 1 duplex RT-qPCR was performed (with 1/8th of spike-in control RNA). Cq values were generated using the FastFinder software v3.300.5 (UgenTec). Only batches were approved with a clean negative control and a positive control in the expected range.
Assembly of positive Cq value distribution
First, a subset of full 96-well RNA plates is selected containing less than 10 positives. The latter selection criterium is introduced to filter out plates originating from high COVID-19 positive rate circumstances, such as hospitals, to avoid putative bias towards high viral loads. Only plates are retained with a positive control value that is within two standard deviations of the mean positive control value of all filtered plates. Next, in order to correct the Cq values for inter-plate variation, the difference of the average positive control Cq values per qPCR plate from the overall mean positive control Cq is calculated. The Cq values in each qPCR plate are then corrected by the qPCR plate-specific difference from the mean. Supplemental Figure 1 displays the distribution of the corrected Cq values of the positive samples. Finally, by inspecting this histogram, we dismiss all Cq values larger than 37 as noisy data, resulting in a final set of 1632 positive Cq values.
Simulation of 1D and 2D pooling strategies
Simulations of are run using R 4.0.1. First, several cohorts of 100 000 patients are repeatedly simulated with varying fractions f, defined by f = 10−x with x = 4,3.95,…,1, of positive cases (resulting in 61 cohorts of 0.01% to 10% prevalence). This is done five times, resulting in five replicate cohort per prevalence (302 cohorts). The Cq values of the positive samples are sampled with replacement from the set of 1632 positive Cq values. Next, the patients are randomly separated into pools depending on the pooling strategy that is simulated. The pooling strategies that were simulated are 1×4, 1×8, 1×12, 1×16, 1×24 (all 1D), and 8×12, 12×16 and 16×24. The Cq value of the pool was calculated as follows:
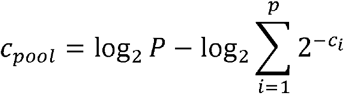
With cpool the Cq value of the pool, the number of samples in the pool, the number of positive samples in the pool, c1,c2,…,cp the Cq values of the positive samples. If the Cq value of the pool is smaller than 37, it is classified as a positive pool. For 1D pooling, only samples in positive pools are retained and the remaining individual Cq values were checked to be positive. For 2D pooling, the Cq values of the differently sized pools are checked simultaneously and the samples in negative pools are removed, after which all Cq values of the remaining samples are checked individually. Samples that were retained after the testing of the pools and had an individual Cq lower than 37 are classified as positive, all other samples are classified as negative.
The sensitivity is calculated as:
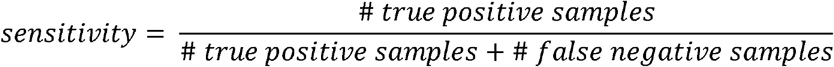
The analytical efficiency gain is calculated as:
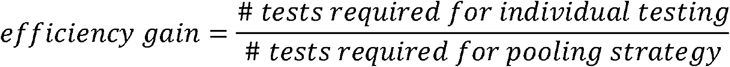
In all simulations, the number of tests required for individual testing is equal to the number of samples.
Data Availability
The code and Cq values are available on https://github.com/jasperverwilt/covidpooling. Cq values will be available as RDML file in the RDMLdb database.
Authors’ contributions
Conceptualization: J.Va., P.M. and J.Ve.; Methodology: J.Va., P.M. and J.Ve.; Software: J.Ve.; Formal Analysis: J.Ve.; Resources: J.Va. and P.M.; Data Curation: J.Ve.; Writing - Original Draft: J.Va. and J.Ve.; Writing - Review & Editing; J.Va., P.M. and J.Ve.; Visualisation: J.Va. and J.Ve.; Supervision: J.Va and P.M.; Project Administration: J.Va. and P.M.
Data availability
The code and Cq values are available on https://github.com/jasperverwilt/covidpooling. The Cq values are available as an RDML file in the RDMLdb database17, under ID 2008AA74.
Supplemental Figures
The binned distribution of Cq values of all full 96-well RNA plates with good controls and less than 10 positives. The Cq values are corrected by calculating the difference between the mean positive control Cq value per 384-well qPCR plate from the overall mean of the positive control Cq values. Grey bars indicate the Cq values classified as noise.
Cq value distributions for false negatives (FN) and true positives (TP) for different pooling strategies. Each data point represents a Cq value from a replicate simulation with a set prevalence.
Distributions of the average sensitivity for the simulations in each group. Each data point is the median sensitivity over five simulations.
Cumulative sensitivities calculated for all Cq values up to a cut-off Cq for each strategy. All true positives and false negatives over five replicate simulations for each sampled Cq value are counted and used for calculation of the sensitivity up to the cut-off Cq. The data is filtered for prevalences of 0.01%, 0.1%, 1% and 10% and colored accordingly.
Acknowledgements
We are grateful for the data from the Belgian federal taskforce for COVID-19 qPCR testing.
Footnotes
The data was uploaded in the RDMLdb database and the ID is provided.












