Abstract
Background The rising COVID-19 pandemic caused many governments to impose policies restricting social interactions. These policies have slowed down the spread of the SARS-CoV-2 virus to the extent that restrictions can be gradually lifted. Models can be useful to assess the consequences of deconfinement strategies with respect to business, school and leisure activities.
Methods We adapted the individual-based model “STRIDE” to simulate interactions between the 11 million inhabitants of Belgium at the levels of households, workplaces, schools and communities. We calibrated our model to observed hospital incidence and seroprevalence data. STRIDE can explore contact tracing options and account for repetitive leisure contacts in extended household settings (so called “household bubbles”) with varying levels of connectivity.
Findings Household bubbles have the potential to reduce the number of COVID-19 hospital admissions by up to 90%. The effectiveness of contact tracing depends on its timing, as it becomes futile more than 4 days after the index case developed symptoms. Assuming that children have a lower level of susceptibility and lower probability to experience symptomatic SARS-CoV-2 infection, (partial) school closure options have relatively little impact on COVID-19 burden.
Interpretation Not only the absolute number and intensity of physical contacts drive the transmission dynamics and COVID-19 burden, also their repetitiveness is influential. Contact tracing seems essential for a controlled and persistent release of lockdown measures, but requires timely compliance to testing, reporting and self-isolation. Rapid tracing and testing, and communication ensuring continued involvement of the population are therefore essential.
Introduction
By the end of June 2020, about 6 months after its initial detection, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) had caused officially over 10 million COVID-19 cases and over 0.5 million deaths around the world [1]. These estimates are conservative due to under-reporting. As the pandemic rose, there was an urgent need to understand the transmission dynamics and potential impact of COVID-19 on healthcare capacity and to translate these insights into policy. Mathematical modelling has been essential to inform decision-making by estimating the consequences of unmitigated spread in the initial phase as well as the impact of non-pharmaceutical interventions on these consequences. In order to assess the impact of gradually releasing society’s lockdown while keeping the spread of the virus under control, requires detailed models to simulate the (non-)propagation of COVID-19. To this end, it is important to capture the heterogeneity in social encounters accounting for a low number of intense contacts (e.g., between household members) and a high(er) number of more fleeting contacts (e.g., during leisure activities, commuting, or in shops) [2].
Individual-based transmission models allow for flexibility to cope with chance, age or context, which is especially of interest to study exit strategies involving school, workplace, leisure activities and micro-scale policies [3, 4]. Individual-based models (IBMs) pose a high burden on data-requirements, implementation and computation, however, the increasing availability of individual-level data facilitates thorough evaluation of specific intervention measures.
Understanding the interplay between human behavior and infectious disease dynamics is key to improve modelling and control efforts [5]. Social contact data has become available for numerous countries [6, 7] and has proven to be an invaluable source of information on the transmission of close contact infectious diseases [8, 9]. Social contact patterns can be used as a proxy for transmission dynamics when relying on the “social contact hypothesis” [8]. Disease-related proportionality factors and timings enable matching age-specific mixing patterns with observed incidence, prevalence, generation interval and reproduction number. In models social contact pattern data can be adjusted to simulate behavioural change and assess intervention strategies that aim to influence contact patterns [5].
Given the rising number of confirmed COVID-19 cases and hospital admissions in Belgium at the beginning of March 2020, all schools, universities, cultural activities, bars and restaurants were closed from 14th March onward. Additional measures were imposed on 18th March, with only work-related transport of essential workers allowed, and teleworking made the norm (termed “lockdown light”). Hospital occupancy peaked around 15th April, and slowly declined afterwards [10]. Restrictive measures were gradually lifted from 4th May onward. There remains substantial uncertainty on the extent to which people complied with physical distancing guidelines and how public awareness and interventions modified social contacts before, during and after the lockdown. More specifically, did people mix more in specific bubbles (or clusters) and what has been the effect of keeping distance, increased hygiene measures and wearing face masks? The nature of social contacts before and after the lockdown undoubtedly changed, and this affects the proportionality factors linking “contacts” with “transmission”. Social mixing patterns represent a key uncertainty in COVID-19 prediction models and is therefore central to our analysis.
In what follows, we analyse the effect of repetitive leisure contacts in extended household settings (so called “household bubbles”) on the transmission of COVID-19 and explore contact tracing strategies with respect to coverage, sensitivity and timing. Our analyses are based on the open-source IBM “STRIDE”, fitted to COVID-19 data from Belgium, with particular focus on transmission dynamics from adaptive social contact patterns.
Methods
Model structure
This work builds on a stochastic individual-based simulator we developed for influenza [11, 12] and measles [13]. Our model represents the population of Belgium, covering 11 million unique individuals, and runs in discrete time steps of 1 day, accounting for adjusted social contact patterns during weekdays, weekends, holiday periods, illness periods, all under the influence of public awareness and of imposed policy measures. More details on the model structure, population, social contact patterns and stochastic realisations are provided in Supplementary Material.
Social contact patterns
Social contact patterns for healthy, pre- and asymptomatic individuals are parameterized by a diary-based study performed in Belgium in 2010-2011 [14, 15]. Contact rates at school and at work are conditional on school enrolment and employment, respectively. We account for behavioral changes of symptomatic cases using observations made during the 2009 H1N1 influenza pandemic in the UK [16], by reducing presence at school and work with 90%. Based on the same study, we reduce community engagement with 75% when experiencing symptoms. Transmission-relevant contact behavior within the household is assumed not to change when a household member develops symptoms.
Household bubbles
We define a “household bubble” as a unique combination of 2 households in which the oldest household members cannot differ more than 3 years in age and are linked via their community contacts during weekends. The age-specific component is included to reduce inter-generational mixing but we perform a sensitivity analysis with age-differences of 20 and 60 years. We also test the effect of household bubbles of 3 and 4 households. The assignment of household bubbles in STRIDE proceeds in a random order. At the point at which a matching household is no longer available, remaining household members are not assigned to any household bubble. This procedure enables us to assign ±95% of the population to a household bubble. These bubbles are exclusive and remain fixed throughout the simulation from 10th May onward.
We assume households in a social bubble to be fully connected 4 days out of 7 (i.e., the contact probability between any two bubble members per average day is 4/7 = 0.57). We also test higher and lower levels of connectivity, 7/7 and 2/7 days per week, respectively. Social contacts in a household bubble are implemented as a substitute of leisure contacts in the community and can be seen as repetitive leisure contacts with the same individuals. Therefore, the community contacts are reduced in proportion to the household bubble mixing to keep the overall contact rate unchanged. We also test household bubbles consisting of 3 and 4 households, where the number of household bubble contacts exceeds the number of simulated community contacts in our scenarios, so the total number of contacts increased. Symptomatic individuals are still assumed to homeisolate, which implies they mix only with their fellow household members, and they have no contacts with members of other households in their household bubble.
Disease natural history
The health states in the IBM follow the conventional stages of susceptible, exposed, infectious and recovered. The duration of each stage, together with symptom onset and duration, are sampled for every individual using the values and distributions shown in Table S2.
Parameter estimation
We estimated (pre-)lockdown transmission parameters and age-specific hospital admission probabilities given symptoms by minimizing the sum of squared residuals of the predicted and reported hospital admissions [10] and serial (sero)prevalence [17, 18]. STRIDE allows to compute the average number of secondary cases upon recovery, i.e. the effective reproduction number over time (Re). The per-case average number of secondary cases 7 days prior to lockdown (which can be interpreted as the basic reproduction number, R0) was estimated to be 3.41, which is in line with estimates from a meta-analysis [19] and other modelling studies for Belgium [18, 20]. More parameter details are provided in the Supplementary Material.
Contact tracing strategy (CTS)
We implement contact tracing strategies (CTS) to assess its impact on reducing transmission. For each index case in the CTS, STRIDE keeps track of all unique contacts upon infection. One day after symptom onset, the index case is placed in self-isolation. Three days later, all these unique contacts are assumed to be traced and tested at a success rate of 90% for household members, and 50% for non-household members. Given the serial process of tracing, testing and isolating, all these three components should be successful in order to have an impact. We estimate the impact of CTS assuming 50% of the symptomatic cases can be contacted, despite the presumption of sufficient tracing capacity. We assume a false negative predictive value of 10% for the testing part, as a combined outcome of sampling, lab-testing and clinical assessment of the treating physician. We performed sensitivity analyses on the timing and contact tracing assumptions.
Scenario analyses
We define all scenarios by combinations of “location-specific social mixing”, relative to pre-pandemic observations. By varying percentages of contacts at different locations, we implicitly assume people either make fewer contacts compared to the pre-pandemic situation or the contacts they make are less likely to lead to transmission (e.g. some transmission will be prevented by more frequent hand washing, distancing or the use of masks [21]). For instance, if we state social mixing at workplaces increased from 20% to 40%, we estimate the impact of “what if the risk of acquiring infection at work doubles compared to during lockdown, though remains still 60% less than in pre-pandemic times”. Table 1 presents the social mixing details for each scenario and Table S4 summarizes the temporal aspects.
B2B: business-to-business, HH: household, CTS: contact tracing strategy, w/o: without, PM: precautionary measures.
In our baseline exit scenario, we accounted for an increase of Business-to-business (B2B) mixing (i.e., contacts while at work) up to 40% of the pre-pandemic observations from 4th May. Business-to-consumer (B2C) and leisure transmission is harder to single out using social contact data within our model structure. To model the relaunch of economic activities and other (leisure) activities in the community, we incorporated a limited increase of community mixing up to 30% in our scenario analyses starting from 25th May. Increasing the transmission potential earlier produced model results that did not match the observed hospital admissions up to 8th June. We do not claim that the increase of community mixing is restricted to 30% or will remain at 30%, but we provide insights of its influence up to 30%.
For schools, we assumed a 50% reduction of transmission due to precautionary measures (smaller class groups, class separation, increased hand hygiene, etc.). We performed sensitivity analyses to explore the effect of distancing measures in schools. We aligned the baseline scenario with the regulations and timings for Belgium (see Table S4). In addition, we included also more general scenarios for re-opening pre-, primary and secondary schools from 18th May onward to make our analysis more explorative. We model, in line with reality, that all schools close on 1st July, in line with the start of the national summer holiday period.
The Belgian government relaxed restrictions on 10th May by allowing additional contacts within the household context. We adopted a strict approach using household bubbles of two households of a similar generation based on the age of the oldest household member. We did not include additional region-specific distancing measures for June, though they are indirectly included in our scenario analysis.
Age-specific susceptibility
To fully explore age-specific effects, especially for school-related scenarios, we additionally calibrated our transmission model assuming that children (0-17y) are only half as susceptible compared to adults (+18y) [22]. The methods are provided in Supplementary Material.
Results
Given the unpredictable nature of social contacts in the weeks and months after the lockdown, we opted to simulate a range of social contact assumptions for each scenario, as listed in Table 1. In our baseline scenario, we assume an increase in social contacts related to B2B, B2C, leisure, and school re-opening. Figure 1 presents the predicted hospital admissions over time given moderate increases of location-specific social mixing with and without household bubbles and contact tracing. The prediction intervals represent the combination of uncertainty on social mixing behavior and stochastic effects, and clearly decrease with a CTS and repetitive contact patterns within household bubbles.
The prediction intervals represent the combined uncertainty of behavior and stochastic effects. The bottom plots show the effective reproduction number (Re). The dots present the reported hospital admissions for Belgium and Table 1 provides more info on scenario 1, 10 and 17, respectively.
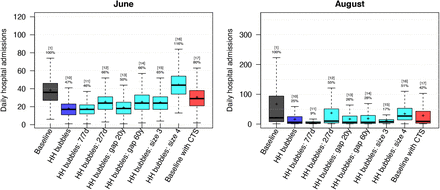
We analysed the effect of social mixing within household bubbles (Table 1) and present the distribution of the predicted hospital admissions for June and August in Figure 2. Our predictions are driven by the combined uncertainty of people’s behavior and stochastic events. It should be noted that the distributions depend on our scenario definitions so that the mean and median values do not have a meaning on their own. These summary statistics are merely used to show relative differences across scenarios. For instance, the household bubbles in scenario 10 could reduce the monthly average number of hospital admissions by 50% in June and by 75% in August as compared to the baseline scenario.
The results are presented as the median, the 75% (box) and 95% (whiskers) percentile and average (cross) of the scenario results due to mixing uncertainty and stochastic effects. The numbers on top of the whiskers indicate the scenario id from Table 1 and the relative change in the scenario average with respect to the baseline. HH: Household, CTS: contact tracing strategy.
If household bubbles are fully linked 7/7 days per week, and most people do not have other leisure contacts outside their household bubble, the monthly average number of hospital admissions reduced by 90% in August. If we assume that household bubbles are less linked (i.e. the equivalent of 2/7 instead of 4/7 days per week), the daily number of hospital admissions slightly increases, but the average number of hospitalizations is still 35% less than the baseline. Increasing the age gap within the household bubble from 3 up to 20 or 60 years, hence allowing multiple generations within one household bubble, seems to have a limited impact on the transmission potential. If we allow household bubbles to consist of 3 households, most people do not have leisure contacts in the “community” anymore. These larger household bubbles might increase transmissions in the short term, but might have beneficial effects in the longer run. If people mix within household bubbles of size 4, their average contact rates increase compared to our included relaxations on distancing within the community. As such, we predict an average increase in hospital admissions in June. However, due to the repetitive nature of the contacts and the depletion of susceptible contacts, the monthly average number of hospital admissions in August is only half of our baseline, despite the increased contact rates.
Contact tracing
Following up symptomatic cases to perform contact tracing, testing and isolation of contacts if infected, has a substantial effect on the average number of daily hospital admissions by 31st August and our corresponding prediction interval (Figure 1 and 2). We predict average reductions in hospital admissions of 20% in June and 58% in August with the CTS in place, assuming that 50% of the symptomatic cases are subjected to contact tracing and comply to home isolation. For all runs within the CTS scenario, accounting for social mixing uncertainty and for stochastic effects, 54% of the infected contacts between May and August were identified within the household, 35% in the community, 11% at workplaces and less than 1% in schools. Our CTS results are based on many assumptions with respect to timing and success rates of tracing, testing, and compliance to home isolation if infected. We performed a sensitivity analysis to challenge our CTS assumptions (90% success rate for household members and 50% for other contacts, 10% false negative tests). The false negative predictive value of testing, due to the sampling, lab-testing and assessment of the treating physician, is important but we still observed a substantial impact of the CTS even with 30% false negative tests (see Figure 3). By varying the success rate of contact tracing per index case, the relative number of hospital admissions range from 60% to 30% of the base case scenario without CTS. Tracing non-household contacts seems to have most impact, since their absolute number can be higher compared to household contacts. However, tracing and testing household contacts, which are more easy to define and accessible via the index case, has already a clear impact. The delay between symptom onset and isolation of the index case seems much more important than the timing of contact tracing and isolation of infected contacts. If index cases are isolated one day after symptom onset (D1), contact tracing will still have effect if started 6 days later (D1+6). If index cases are tested and isolated 6 days after symptom onset (D6), there seems nothing more to gain. We observed a clear drop in the relative hospital admissions when index cases are isolated 4 days after symptom onset.
Timings are expressed relative to symptom onset of index case (D0), and days after testing the index case (e.g., Di+2). All simulations start from the baseline scenario assuming a 30% reduction of community contacts and 60% for workplace contacts. The ‘x’ marks the default settings, which are used if a parameter is not shown.
School re-opening
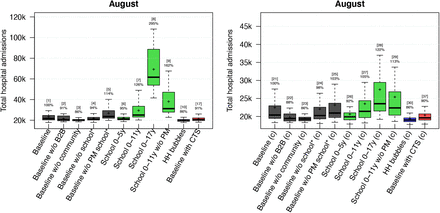
We analysed the effect of location-specific mixing with two assumptions on the susceptibility for children up to 17 years of age: equally susceptible or only half as susceptible compared to adults (+18y) [22]. The results are presented in Figure 4. Starting from the baseline and each time leaving one location-specific re-opening out, we observed most impact of community mixing for both susceptibility-related assumptions. Also the effect of household bubbles and CTS is similar in terms of the predicted cumulative hospital cases by 31st August. As expected, the impact of school re-opening is strongly associated with the assumption on age- specific susceptibility. Assuming that children are equally susceptible compared to adults, we predicted an increase up to 126% and 295% of the hospital cases from our baseline scenario if schools re-open up to primary or secondary schools, respectively. Assuming an age-specific reduction in terms of susceptibility, re-opening primary schools had much less impact on the predicted number of hospital admissions. If all children up to 17y of age would go back to school, we predicted an average increase of hospital cases by 31st August up to 122% relative to our baseline scenario.
The results are presented as the median, the 75% (box) and 95% (whiskers) percentile and average (cross) for all combinations of the contact reductions per scenario. The numbers on top of the whiskers indicate the scenario number from Table 1 and the relative change in the scenario average with respect to the baseline. HH: Household, w/o: without, CTS: contact tracing strategy; PM: precautionary measures at school.
In the baseline and most school re-opening scenarios, we assumed a 50% reduction of school-related transmission due to precautionary measures (PM) such as smaller class groups, class separation, increased hand hygiene, etc. We observed a difference without these measures irrespective of the age-specific susceptibility, though the effect is rather limited if children are only 50% as susceptible compared to adults.
Discussion
Uncertainty on social mixing and contact intensity during and after the lockdown plays a crucial role in this analysis. This is structural uncertainty, which we handled by including different assumptions within our scenarios on tracing, school re-opening, etc. In addition to contact frequency, the contact intensity (duration, intimacy, indoor/outside location, etc.) also plays a role in the transmission dynamics. We defined a baseline scenario based on observations and the assumption that the number of daily hospital admissions would not rise above the previously observed peak. This restricts our assumptions on social mixing and the reduction of physical distancing. This scenario is not meant to represent the “current situation”, but to analyse the relative impact of mutually exclusive scenarios as in comparative effectiveness research. In addition, social mixing in sub-clusters with repetitive contacts, as well as contact tracing by call centres are now both occurring in Belgium. This also explains why our “baseline” might differ from future observations.
Parallel modelling work for the UK [23] showed that social bubbles reduced cases and fatalities by 17% compared to an unclustered increase of contacts. Social bubbles may be extremely effective if targeted towards those small isolated households with the greatest need for additional social interactions and support. Repetitive contacts within household bubbles make them more identifiable, which enhance contact tracing and any kind of CTS.
We found a great potential for CTS to reduce transmission and hospital admissions, but it will most likely not be enough to control future waves. The predictions shown in Figure 1 also account for physical distancing. The relative proportion of symptomatic cases that is included in the CTS of index cases is driving the efficiency. Also, timing is of the essence and contact tracing should start at the latest 4 days after symptom onset of the index case. The short serial interval makes it difficult to trace contacts due to the rapid turnover of case generations [24]. Keeling et al. [2] concluded that rapid and effective contact tracing can be highly effective in the early control of COVID-19, but places substantial demands on the local public-health authorities. We did not include or analyse the enhancing/spiraling effect when infected contacts are subsequently included as index case. This could be one way to reach the number of index cases, which we implicitly included in our strategy. Another effect of this spiraling approach might be a reduction of the workload given overlapping contacts with a previous index case. However, the timing of physical contacts and testing might interfere with this optimization procedure. We did not look into this to focus on the basic principles and stress the potential of CTS.
Kucharski et al. [25] also reported on the effectiveness of physical distancing, testing, and a CTS for COVID-19 in the UK. They concluded that the combination of a CTS with moderate physical distancing measures is likely to achieve control. They used also an IBM with location-specific mixing and transmission parameters and similar natural history of the disease. Their model is different in the number of contacts, which is fixed to 4, and social contact pools for school, work and other, are defined at a lower degree of granularity compared to our model. We are able to identify the class members and direct colleagues of infected individuals, and can confirm their conclusions on CTS and isolation strategies. We both stress the potential of CTS but warn that additional physical distancing measures are required to be successful.
Kretzschmar et al. [26] computed effective reproduction numbers with CTS and social distancing in place by considering various scenarios for isolation of index cases and tracing and quarantine of their contacts. Without a delay in testing and tracing and with full compliance, the effective reproduction number was reduced by 50%. With a testing delay of 4 days, even the most efficient CTS could not reach effective reproduction numbers below 1. We did not express the impact of CTS on the reproduction number, though also found a tipping point in the CTS effectiveness if contact tracing starts 4-5 days after symptom onset of the index case.
School closure is considered a key intervention for epidemics of respiratory infections due to children’s higher contact rates [27, 28], but the impact of school closure depends on the role of children in transmission. Davies et al [22] conclude that interventions aimed at children might have a relatively small impact on reducing SARS-CoV-2 transmission, particularly if the transmissibility of subclinical infections is low. This is also the conclusion from our sensitivity analysis where we assume children (<18y) to be half as susceptible as adults (+18y).
Other IBM applications have been reported [29, 30, 4] to simulate combinations of non-pharmaceutical interventions by targeting transmission in different settings, such as school closures and work-from-home policies. Modelling the isolation of cases in safe facilities away from susceptible family members or by quarantining all family members to prevent transmission has showed substantial impact. Models that explicitly include location-specific mixing are very relevant for studying the effectiveness of non-pharmaceutical interventions, as these are more dependent on community structure than e.g. on vaccination [29]. However, implementing the available evidence into a performant and tailor-made model that addresses a wide range of questions about a variety of strategies is challenging [30, 3].
Although our analysis is applied to Belgium, our findings have wider applicability. We considered the effect of universal adjustments in terms of social mixing (isolation, repetitive contacts, contact tracing). We modelled 11 million unique inhabitants with detailed social contact patterns by age and location. Hence, we can compare model results with absolute incidence numbers in the absence of premature herd immunity effects due to a reduced population size. The latter might be an issue for models that use a scaling factor to obtain final results. Our individual-based model provides a high-resolution, mechanistic explanation of the reproductive number and transmission dynamics that are relevant on a global scale.
Limitations
A model is a simplification of reality and therefore depends on the assumptions made. In addition, our spatially explicit IBM is calibrated on national hospitalization data so uncertainty is inevitably underestimated. As such, we rely on scenario analyses and further sensitivity analyses are necessary. Model results should therefore be interpreted with great caution.
Our IBM is a mechanistic mathematical model that uses conversational contacts as a proxy of events during which transmission can occur. By definition, COVID-19 infection events that occurred through the environment (e.g., contaminated surfaces) are absorbed by these conversational contacts. The best data at hand to calibrate our transmission model are the reported hospital admissions, which lags the occurrence of infections by approximately 2 weeks. This implies additional limitations.
Recent work also shows that the use of antiviral drugs in combination with CTS can reduce the effect of local outbreaks [31]. This kind of pharmaceutical interventions could be incorporated in future applications of the STRIDE model. We focused on the general population and did not consider care homes separately in our analysis, mainly because the hospital data available to us did not distinguish between admissions from care homes and the community. We did not include aspects related to travel or weather conditions (UV light, humidity, temperature) which may impact both transmission and social contact behaviour in ways that are currently largely unknown.
Data Availability
We provide all code and data in an open-source GitHub repository: https://github.com/lwillem/stride
Availability of data and materials
We provide all code and data in an open-source GitHub repository: https://github.com/lwillem/stride
Competing interests
The authors have nothing to disclose.
Funding
LW, SA and NH gratefully acknowledge support from the Fonds voor Wetenschappelijk Onderzoek (FWO) (postdoctoral fellowship 1234620N and RESTORE project – G0G2920N). This work also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (PC, SAH, NH, grant number 682540 – TransMID project; NH, PB grant number 101003688 – EpiPose project). The resources and services used in this work were provided by the VSC (Flemish Super-computer Center), funded by the Research Foundation – Flanders (FWO) and the Flemish Government. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Authors’ contributions
LW, PB and NH conceived the study. SA, PC, CF, SH, SM, OP and JW contributed to the data collection and analysis. EK and PL contributed to the software development. All authors contributed to the final version of the paper and approved the final manuscript.
Each member of the SIMID COVID-19 team contributed in processing, cleaning and interpretation of data, interpreting findings, contributed to the manuscript, and approved the work for publication.
SUPPLEMENTARY MATERIAL
S1 Model population
This work builds upon a stochastic individual-based simulator, STRIDE, we developed for influenza [1, 2] and measles [3]. Our individual-based model has a particular focus on social contact patterns by modelling each individual as part of “contact pools”, representing a household, school-class, workplace, or community.
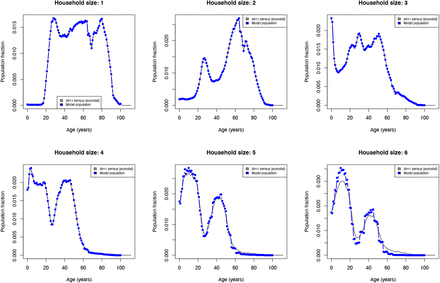
Household combinations, which specify the age of each member, are based on Belgian census data from 2011. We had to process the census data to ensure anonymization by excluding households containing 7 or more individuals (3.5% of population) and by using age groups for household combinations with a frequency of less than five. As such, we aggregated ages into 2-year intervals for individuals aged 0-25 and 5-year intervals for individuals over 26 years of age. If the frequency of an aggregated household composition still remained less than five, the households were excluded (0.7% of population). Next, we re-sampled ages from the age intervals to settle each household combination for our model population. We matched our resulting household data with summary statistics for household size and noticed an under-representation of large households containing children. Therefore, we duplicated 25,000 and 45,000 randomly chosen households of size 5 and 6, respectively, in which the second youngest household member was of age 0-25. These numbers were chosen to obtain matching distributions regarding household size, age in the population and age per household size. Figures S1 and S2 present summary statistics from the model population and Belgian census data.
Numbers are expressed in million (M).
We build our population by sampling households and assigning them to geographic locations based on the population census of 2001. Our population of 11 million people is closed, meaning that no births or deaths occur during the simulation, nor emigration or immigration. Children are assigned to a daycare center (0–2 years old), preschool (3–5 years old), primary (6–11 years old), secondary (12–17 years old) or tertiary (18–23 years old) school based on Belgian enrolment statistics from Eurostat [4]. Daycare centers in Belgium comprise on average 8 infants [5], with a skewed distribution up to 18 infants. School classes in pre-, primary and secondary schools contain on average 19, 20 and 20 children, respectively, which is based on government statistics [6]. Students enrolled in tertiary schools are assigned to groups of 50 fellow students. Adults (18–64 years old) are assigned to a workplace or a daycare center/school class based on age-specific employment data and aggregated workplace size data from Eurostat [4]. We included one adult per 8 children in a daycare center and one adult per class in the pre- and primary school setting. Each “workplace” represents professional contacts in line with “business-to-business” (B2B) activities. The size of the workplaces is based on data from Eurostat and categorized into 1-9 (94%), 10-19 (3%), 20-49 (2%), 50-249 (0.8%) and +250 (0.2%) people. Geographic workplace assignment is based on commuting data from the 2001 Belgian census.
To represent leisure activities, family visits, “business-to-consumer” (B2C) and other contacts, the model contains “communities”. Each community is specified by a geographic center based on population density and contains on average 500 individuals. This arbitrary number affects the contact probability but it does not influence the contact rate. Each individual is assigned to one of three nearest community centers close to their home to represent weekday interactions and activities. For weekends, individuals can be assigned to the same community center or another one close to home. This community setup allows individuals to have similar contacts during week and weekend days, but prevents a strict compartmentalisation of the population.
S2 Social contact patterns
Social mixing in STRIDE is based on a diary-based social contact study performed in Belgium in 2010-2011 [7, 8]. All participants were asked to record their contacts during one randomly assigned day without changing their usual behavior. They also reported their time-use by activity, location and distance from home. Table S1 provides an overview on how the survey data is used to inform contact pools in the individual-based model. Please note that contact rates at school and at work are conditional upon school enrolment and employment, respectively. During each time step, we match the age- and location-specific contact rate (= number of contacts per day) with the number of individuals in a contact pool (e.g., workplace, school, etc) to calculate the contact probability. We limit the contact probability at 0.999 and always use this maximum in a household setting. Contact probabilities account for reciprocity hence to incorporate age-specific social mixing, we always use the lowest age-specific probability in the Bernoulli trial to predict a contact event.
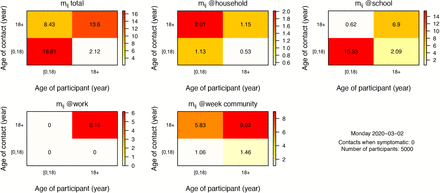
The model allows to track social contacts in the population on a daily basis for a all or a random selection of individuals. The output is aligned with Socialmixr [9] and Socrates [10] to generate and visualise social contact matrices. Figure S3 presents social contact matrices based on 5000 individuals during weekend days and Figure S4 for weekdays before the COVID-19 lockdown.
Participants with more than 20 professional contacts per day (with students, clients, patients, etc.) had to report only the total number and age groups of their Supplementary Professional Contacts (SPC).
These are aggregated rates based on one-year age group data from the model.
These are aggregated rates based on one-year age group data from the model.
S3 Age-specific proportion symptomatic cases
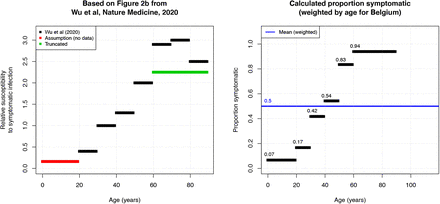
We assumed an overall proportion of symptomatic cases in the population of 50% based on Li et al. (2020) [11]. To obtain an age-specific proportion of symptomatic cases, we combined this population estimate with the age-specific relative susceptibility to symptomatic infection reported by Wu et al. (2020) [12]. Figure S5 presents the age-specific data from [12], which we amended with an assumption for individuals 0-19 years of age. These relative proportions had to be re-scaled and weighted by age, to end up with a population average of 50%. Therefore, we calculated the relative population size by age as:
with Na the population size of age group a, Ntotal the total population size and T the number of age groups. Secondly, we calculated the age-specific proportion of symptomatic cases as:
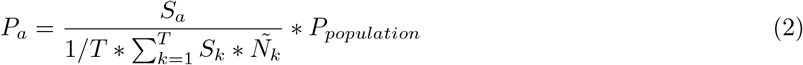with Sa the relative susceptibility to symptomatic infection for age a, Ña the relative population size for age a, and Ppopulation the proportion symptomatic cases on the population level. Figure S5 presents the resulting proportions symptomatic cases by age. Please note that we had to truncate the highest relative susceptibility to symptomatic infection to maintain all age-specific probabilities between 0 and 1. This limitation is caused by the interaction between the age-specific susceptibility and population sizes with the overall proportion of 50%.
Relative susceptibility to symptomatic infection by age based on Wu et al. (2020) [12] (left) and estimated proportion of symptomatic infections (right).
S4 Parameter estimation
After incorporating population and social contact dynamics for Belgium together with the disease history for COVID-19 (Table S2), we estimated the timing of introduction in the Belgian population, the number of initial cases and the transmission probability. We performed a grid search using the sum of squared residuals of the reported [13] and predicted hospital admissions over time to score parameter combinations throughout our analysis. To assess the stochastic robustness of the parametric setting, we calculated the average score of 10 stochastic realisations for each parameter set. Starting our simulations on 17 February with 510 infected individuals was most optimal to match the observed hospital cases. Please note that these parameters are strongly correlated and affected by many other parameters such as hospital admission probability.
Transition parameters are discretized to the modelling time step of 1 day and parameter values are expressed by their mean and 95% confidence interval or interquartile range (IQR), where appropriate. Intermediary model outcomes are calculated from model results 7 days prior to lockdown (i.e. 7-13 March).
The model allows to track the infector, timing and location of each infection. This enables us to compute the average number of secondary cases upon recovery, i.e. the effective reproduction number over time. We calculated summary statistics for the transmission dynamics 7 days prior intervention measures (6-13 March) by estimating the average number of secondary cases, the doubling time of the infected cases and the generation interval (i.e. the time between the infection time of an infected person and the infection time of his or her infector). Table S2 contains the average and confidence interval based on 10 stochastic realisations.
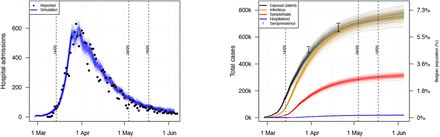
To match the reported hospital admissions up to 4th May 2020, when restrictive measures relaxed, we estimated the reduction in social mixing relative to pre-pandemic social contact patterns. Schools were closed in Belgium except a low number of children that required day care (e.g., if both parents were not able to telework), so we assumed neither social contacts nor transmission at schools. People who could, were coerced into telework and many businesses, unable to guarantee required hygiene en physical distancing measures had to close. All business-to-consumer (B2C) outlets were interrupted except for online ordered home deliveries and shops selling essential goods. We estimated social mixing associated with business-to-business (B2B) activities, and in the community (including B2C) to linearly decrease over a 6 day period from 13th March and reach 20% and 15% of pre-pandemic social mixing on 19th March, respectively. In addition, we assumed additional inter-generational physical distancing with people of 65 years or older in the “community”, expressed by a 90% decrease in contacts with this age group from any other age group. We illustrate the predicted and reported hospital admissions in Figure S6. This figure also present the cumulative number of cases over time in combination with prevalence estimates based on serial serology data.
The cumulative numbers are presented together with confidence intervals from serial seroprevalence data on 30th March and 20th April based on [19].
By matching serial serological survey data [18] and hospital admission data, we estimated age-specific hospital admission probabilities given symptoms. We used the predicted prevalence 0.046 (0.044-0.048) on 30th March and 0.061 (0.058-0.064) on 20 April, based on methodology described in Abrams et al [19]. We estimated the average hospitalization probability over all ages to be 17% and estimated age-specific probabilities (Table S2) based on the observed proportional hospital admissions by age. The weighted hospital probability, when accounting for the age of the predicted cases, was 7%. Note that the hospital admission probability is closely correlated with the age-specific proportion of fully asymptomatic cases and should be interpreted as a combination of these two factors.
S5 Age-specific susceptibility
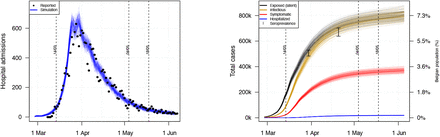
We account for the reduced infectiousness of children via the 50% reduction in infectiousness for asymptomatic cases [11] in combination with the age-specific proportion symptomatic cases, which is only 7% for individuals aged 0-19y. To analyse additional age-specific effects, we also calibrated our transmission model given that children (0-17y) are only halve as susceptible compared to adults (+18y). Since the pre-pandemic social contact patterns remain constant, we had to adjust the transmission probability given contact to obtain the same reproduction number. The estimated contact reductions during the intervention period (April-May) changed to 15% for workplace contacts (instead of 20%) and 13% for community contacts (instead of 15%). The social mixing assumptions with respect to the deconfinement scenarios (after 4th May) did not change. The changed transmission dynamics also alter the age distribution of cases, so we re-estimated the age-specific hospital admission probability to match both the observed (sero)prevalence [18] and hospital admissions [13]. Table refS3 contains the adjusted hospital admission probabilities and transmission summary statistics, pre-intervention, with and without the children’s’ reduced susceptibility assumption. Figure S7 presents the resulting hospital admissions and cumulative number of cases over time.
The cumulative numbers are presented together with confidence intervals from serial seroprevalence data on 30th March and 20th April based on [19].
Transition parameters are discretized to the modelling time step of 1 day. The model outcomes are calculated from model results 7 days prior to interventions (i.e. 7-13 March).
S6 Scenario definitions
We defined scenarios by combinations of location-specific social mixing relative to pre-pandemic observations. By varying percentages of contacts at different locations, we implicitly assumed people either make fewer contacts compared to the pre-pandemic situation or the contacts they made were less likely to lead to transmission. For example, if we increased social mixing at workplaces from 20% to 40%, we predict the impact of “what if the risk to acquire infection at work doubled compared to during lockdown, though still 60% less than in pre-pandemic times”. Table 1 in the main text presents an overview of the social mixing patterns within each scenario. To account for structural uncertainty with respect to B2B-related social mixing, we included 20%, 30% and 40% of the social contacts rates prior lockdown. For community-related mixing, we used 15%, 20% and 30% of the social contact rates prior lockdown. By combining these B2B and community mixing patterns, we ended up with nine social mixing parameter sets and we ran 10 stochastic realisations per parameter set. Table S4 contains temporal aspects of the scenarios and the age-specific “school*” program based on the Belgian regulations.
The age-specific school-reopening as stated by the Belgian government on 24 April is marked as school*.
S7 Platform and technical details
STRIDE is open source software (https://github.com/lwillem/stride) and implemented in C++. The software is portable over Linux and Mac OSX platforms with a recent version of a C++ compiler. To build and install STRIDE, the following tools need to be available on the system: GNU g++ or LLVM clang++ compiler, make, CMake and Boost. To generate documentation, Doxygen and LaTeX are required. The build system for STRIDE uses the CMake tool to compile and install the software almost platform independent. More info is provided in the user manual on Github.
Our model is optimized with a switch to evaluate only the social contacts of the infectious individuals instead of matching every individual with all others within one location. More details on our model optimisations are provided in [1].
The modelling project contains regression tests in the Google Test suite embedded in a Travis continuous integration environment. The test environment has been created and maintained during model development for influenza and measles, and additional unit tests were added during this analysis. We implemented a baseline test for COVID-19 and test also physical distancing, household bubbles and contact tracing.
We implemented an “rSTRIDE” framework in R to handle the design of experiments, to run all parameter sets and analyse the output. Different serial STRIDE simulations are run in parallel using the “doParallel” package and the aggregation of summary statistics, prevalence, incidence and social contacts is automated. The synthetic population of 11 million individuals is computed once using R and loaded onto the C++ simulator for every new simulation.
All results presented in this manuscript are generated on the VSC-cluster “Leibniz”, a NEC system consisting of 152 nodes with two 14-core Intel E5-2680v4 Broadwell generation CPUs connected through a EDR InfiniBand network. We ran only single-node jobs. Each run from our baseline scenario required ±21 minutes.
Acknowledgements
The authors are very grateful for access to the data from the Belgian Scientific Institute for Public Health, Sciensano, and from the Vaccine & Infectious Disease Institute (VaxInfectio), University of Antwerp. We acknowledge support from the Antwerp Study Center for Infectious Diseases (ASCID) and Flemish Super-computer Centre (VSC) with special thanks to the CalcUA-team (FB and SB).
Abbreviations
- STRIDE
- Simulator for the TRansmission of Infectious DiseasEs
- HH
- Household
- w/o
- without
- B2B
- Business-to-Business
- B2C
- Business-to-consumers
- ICU
- Intensive Care Unit
- CTS
- Contact Tracing Strategy
- PM
- Precautionary Measures
References
