Using real-world contact networks to quantify the effectiveness of digital contact tracing and isolation strategies for Covid-19 pandemic

1 Introduction

As of mid-May 2020, the COVID-19 pandemic has reached almost 4.5 millions detected cases worldwide,¹² overwhelming the healthcare capacities of many countries and thus presenting extraordinary challenges for governments and societies.^13–16 At present, there are no known effective pharmaceutical treatments, and a vaccine is estimated to be approximately one year away.¹⁷ Non-pharmaceutical interventions (i.e. social distancing, wearing masks and reinforced hygiene) are therefore currently the main path towards mitigating the intensity of the pandemic and return society to near-normal functioning.

In the early stages of the pandemic, rigorous restrictions have been effective in curbing the spread of SARS-CoV-2.^13,18–25 Using lock-downs and quarantine, countries have managed to limit contagion and reduce the effective reproduction number R₀, lowering the number of daily new cases and hospitalizations. Many areas have now entered (or are entering) a transition phase, slowly lifting the mobility restrictions. The transition phase is potentially fragile, and an effective and affordable long-term plan is required to avoid resurgences of infections and new outbreaks.²⁶ This is particularly pressing given the possibility that the COVID-19 pandemic will come in waves as anticipated by several early models,^27,28 and since the number of people who have been infected is still far from ensuring herd immunity.¹⁶

Despite their efficacy, large-scale quarantine and lock-down strategies carry enormous costs and not all countries can afford such measures,¹⁹ due to their consequences on economic and social stability. Moreover, population-wide measures are non-specific: in a situation where most of the individuals are not infected, it is highly sub-optimal to lock-down the whole population, and interventions at smaller scale, selectively targeting individuals at higher risk of spreading the disease, are more desirable.

While the testing and isolation of symptomatic cases is certainly crucial, it is insufficient in the case of SARS-CoV-2, since many contagion events take place before symptom onset^1,29,30 and a substantial fraction of infected individuals do not develop symptoms at all.^31,32 Thus, the identification and isolation of infected cases must be coupled with a strategy for tracing their contacts, who may either have transmitted the virus or have been infected before the onset of symptoms by the detected case, quarantining them and monitoring their health status.³³ In this context, recent modeling studies have shown^1,34–36 that contact tracing may reduce epidemic spreading and the efficacy of its realization – contagious contact identification and timing – plays a pivotal role.

Contact tracing is typically performed manually, i.e. by direct interviews of cases. While this ensures a thorough assessment of the actual risk of individuals who have been in contact with these cases, it is a relatively slow process and is highly labor intensive:^37–39 it can be efficiently implemented only when the number of infected individuals is low. In addition, the accuracy of manual tracing is limited by the ability to recall and identify close proximity contacts: brief contacts have a lower probability of being recalled and contact durations are in general overestimated in retrospective surveys.^{40, 41} Thus, technologies that use proximity sensors are currently being considered as fundamental tools to complement manual tracing. Specifically, the idea is to leverage the widespread dissemination of smartphones to develop proximity-sensing apps based on the exchange of Bluetooth signals between smartphones,^{1,6–11,42,43} which makes it possible to build privacy-preserving contact tracing frameworks.⁶

The efficacy of app-based contact tracing has been discussed in several recent papers.^2,44–47 Here, we start from the work by Fraser et al.,³ recently adapted to the COVID-19 case.¹ In short, the authors propose a mathematical model where the temporal evolution of a spreading process is determined by recursive equations that update the number of infected people in the population based on the (evolving) infectiousness of the infected individuals and on two parameters describing the interventions, ε_I and ε_T. These parameters represent the ability to identify and isolate infected people and the ability to correctly trace their contacts, respectively. Assuming an exponentially growing trend for the number of infected people (which is typically applicable in early phases of an epidemic outbreak) the authors identify a stationary solution and study how the growth rate depends on the intervention parameters. While this approach provides a simple way to quantify the effect of isolation and tracing strategies in an epidemiological model, it is subject to several limitations, both from the modeling and from the applicability point of view. First, the assumption of full homogeneous mixing in social networks is an important limitation in epidemic modeling,^4,5,48,49 and realistic network architectures might be particularly important in the case of contact tracing.⁴⁴ Second, the mathematical framework is limited to an exponential growth. Third, the parameters ε_I and ε_T are assumed to be independent.

Here, to better understand the concrete efficacy of real-world contact tracing, we dramatically expand the realism of the approach described above on these three aspects. First, we provide a realistic quantification of the tracing ability by performing simulations of spreading processes and of contact tracing strategies on several real-world data sets collected across different social settings (i.e., a university campus, a workplace, a high school).^50-52 This allows us to estimate the actual “tracing ability” parameter ε_T for different possible tracing policies (i.e., the thresholds considered to define a contact measured by the app as “at risk”) and for different values of ε_I (section 4.1). The parameter ε_T can then be inserted into the mathematical model to study the impact of the tracing policy on the spread. In order for app-based contact tracing to work properly, it is indeed necessary that the potential infection events detected by smartphones constitute a reasonable proxy for real-world infection dynamics. However, little is currently known about the relationship between actual biological infections and the type of proximity interactions detected using smartphones. Here, we assume that the probability of a contagion event occurring during a proximity event between a healthy and an infected individual depends both on the duration and on the distance between those individuals (along with other epidemiological variables such as the infectiousness of the individual – see Supplementary Information A). Note that, as Bluetooth signal strength is not trivially converted to a distance,⁵³ we rely – as the apps being currently developed will do⁶ – on the received signal strength as a proxy for distance.

Secondly, we restructure and generalize the mathematical framework of the approach^1,3 to avoid assumptions regarding the functional form of the epidemic growth, which is therefore not assumed to be exponential. Moreover, we have modified the epidemiological part of the model according to recent literature on COVID-19,^54–56 to fully consider asymptomatic cases and the delay in isolating individuals after their identification (Supplementary Information B).

Our third key contribution concerns the modeling and the detailed investigation of the contact tracing procedure. We devote a particular attention to the tracing parameter ε_T, which unavoidably depends on the ability to detect infected people whose contacts can then be traced: in other words, ε_T is not independent from ε_I. Moreover, when gathering information on the recent contacts of an infected individual, it is obviously not possible to know which interactions, if any, really did correspond to a contagion event. Any contact tracing policy is thus based on thresholds on duration and proximity to define the risk associated with each contact. Among those, some are infected while others are not. The latter correspond to “false positives”, i.e., healthy individuals who will be preventively quarantined. Similarly, among the contacts considered as non-risky by the contact tracing, some might actually be infected (“false negatives”). The use of real-world data makes it possible to evaluate the number of false positives and false negatives for various policies, together with their effectiveness in containing the spread. The proportions of false positives and negatives represent crucial information as the acceptability of contact tracing apps depends on these outcomes. On the one hand, a low number of quarantined, or mis-calibrated policies that do not correctly identify the individuals with the highest probabilities of having contracted the virus, can unwittingly omit many potential spreaders. On the other hand, highly restrictive policies might require to quarantine large numbers of individuals, including healthy ones, with a consequent high social cost.

Overall, our approach allows us to evaluate the effect of different contact tracing policies not only on the disease spread but also in terms of their impact on the number of quarantined individuals. By clearly identifying the relevant variables, we can show how to vary them separately and understand which measures the system is more sensitive to, providing insights on how to tune and adapt policies to be maximally effective. This novel combination of a well-established epidemic model with state-of-the-art, empirical interaction data collected via Bluetooth technologies or via similar radio-based proximity-sensing methods, allows us to understand the role played by intrinsic limitations of app-based tracing efforts, affording an unprecedented viewpoint on the ambition of achieving containment with app-based interventions. Namely, we are able to test and quantify the role that a real contact network plays both for the infectiousness of a contact and for the ability of a policy to detect it and to respond optimally. It is important to emphasize again that stylized mathematical models on the performance of app-based approaches disregard important heterogeneities of high-resolution contact network data – both topological and temporal – that are known to shape infectious disease dynamics.⁴⁹ By studying contact tracing interventions on empirical data that include such complex features, we make a first step at bridging this gap, obtaining several new insights.

First, we show that if the isolation of infected individuals is only implemented after symptom onset, the containment of the epidemic becomes challenging, due to the large fraction of asymptomatic individuals. The only way to stop the spreading in this case requires the maximum efficiency of both isolation and tracing procedures. On the other hand, a combination of self-reporting and randomized testing allows for the design of effective contact tracing policies.

Finding a tracing policy that is able to contain the epidemic is a non-trivial task, and our aim is to quantify and describe the properties that makes a policy effective, in terms of duration and signal strength thresholds, tracing period of time and isolation efficiency. Furthermore, we show that isolation and tracing measures are only as effective as the technology they use: No tracing is possible if adequate spatial and temporal resolution are not available.

Even if it is clear that the choice of a particular policy should be primarily guided by its effectiveness in containing the virus, we find that not all successful policies are equal. In particular, we demonstrate that beyond a certain accuracy, stricter policies do not improve the containment, while on the other hand a successful reduction of the number of non-quarantined infected people (and thus containment of the epidemic) is possible only if mirrored by a significant increase of the number of healthy people that are unnecessarily quarantined. Comparing policies also at this level allows to improve their design and to reduce their side effects.

2 Results and Discussion

We evaluate the effect of measures based on the deployment of a digital contact tracing app on the mitigation of the Covid-19 pandemic. As we do not consider geography nor large-scale mobility, our modeling can be considered as referring to a limited geographical area, similarly to previous modeling efforts.^1,35

In particular, we assume that two types of interventions are possible to limit the spread of the virus.

First, infected individuals, who are either symptomatic and self-reporting or identified through randomized testing, are isolated. Second, individuals who have had a potentially contagious contact with those last are preventively quarantined. The last step is assumed to be implemented via an exposure notification app on their smartphone. Schematically, if a detected infected individual has the app, the anonymous keys that her/his device has been broadcasting through Bluetooth in the past few days are exposed. The app of the individuals with whom s/he has been in contact in the past days recognizes these keys as stored on their own device and calculates a risk score. If the risk score obtained by an individual is above a certain threshold (determined by the considered policy), the contact is “at risk” and the individual is quarantined, even if s/he does exhibit any symptom. We refer to⁶ for more details on the implementation on privacy preserving apps. Our research question is whether or not it is possible to contain a COVID-19 outbreak by means of these two measures.

We introduce the concept of potentially contagious contact into a mathematical framework where the epidemic evolution is governed by a model based on recursive equations, inspired by the work of Fraser et al.,³ and recently adapted to the Covid-19 case.¹ This model quantifies the number of newly infected people at each time interval, given a characterization of the disease in terms of infectiousness and manifestation of symptoms. The model is specifically designed to consider the two interventions described above, whose effectiveness are quantified by two parameters ε_I, ε_T varying from 0 to 1 (where ε_I = 0 means “no isolation” and ε_I = 1 represents a perfectly successful isolation of all individuals who are found to be infected, either via self-reporting or testing; ε_T quantifies instead the efficacy contact tracing).

Here, particular attention is devoted to the study of the dependence of ε_T on ε_I, and to assess which policies are actually achievable given the realistically deployable technology and resources. Indeed, we couple this model with a realistic quantification of the effect of these two measures based on real-world contact and interaction data. The following results are obtained by the model and the simulation using the parameters defined in Supplementary Information A, and the Copenhagen Networks Study (CNS) dataset⁵⁰ that describes real proximity relations of smartphone users measured via Bluetooth (see Section 4.1). In the Supplementary Information we address two different scenarios corresponding to two other datasets collected by the SocioPatterns collaboration using radio-frequency identification tags.^51,52

We emphasize that a realistic quantification of the tracing ability is each time obtained by simulating the epidemics on a dataset, but the controllability of the disease is assessed by the general mathematical framework and is therefore not bounded by specific datasets.

We consider five different policies (Table 1) that correspond to different threshold levels on the signal intensity, considered as a proxy of distance, and on the duration of the contact (recall that Bluetooth does not measure distances precisely so that all real-world implementations are based on thresholds on Received Singal Strength Indicator (RSSI) values). We additionally assume that the app of an individual keeps memory of the anonymous keys received from other apps, which represents a history of the past contacts, during n days. Here, we consider n = 7 days, as we found (Supplementary Information C.2) that a longer memory does not produce any significant improvement. Overall, this implies that we consider here a simplified version of the app, which does not compute risk scores but is simply able to remember the contacts corresponding to a sufficiently close and lasting-long proximity during n days, while contacts below the thresholds are not stored. In addition, each policy is tested with an isolation efficiency with values ε_I = 0.2, 0.5, 0.8, 1, which encodes isolation capacities ranging from rather poor to perfect isolation of any symptomatic or tested positive person.

A fundamental difference between the policies is in the fraction of contacts that are stored by the app. Figure 2 shows the distributions of the RSSI and the contact duration of all the interactions in the CNS dataset. It is clear that most of the contacts have short duration and low signal strength (and are thus likely random contacts), but long lasting durations are also observed, with overall a broad distribution of contact durations as typical from data on human interactions.^53,57

• Download figure
• Open in new tab

Figure 1:

The contacts of an individual’s carrying an app-equipped smartphone with other app-adopters are registered through the app. As soon as an individual is detected as infected s/he is isolated, and the tracing and quarantine policy is implemented. Depending on the policy design, the number of false positives and false negatives may vary significantly.

• Download figure
• Open in new tab

Figure 2:

Distribution of the duration (Figure 2c) and signal strength (taken as a proxy for proximity, Figure 2b) of the contacts in the CNS dataset. Figure 2a gives a scatterplot of signal strength vs duration for all contact events in the dataset, and displays the thresholds defining the various policies.

The thresholds defined by the tracing policies in Table 1 determine the fraction of contacts that are traced by the app, and only the contacts within the specified regions are considered when determining who is alerted by the app and hence quarantined. Figure 2 highlights how both spatial and temporal resolutions exhibit a highly non-linear and non-trivial effect on the capability of tracing more individuals who have been in contact with an infected one. Panels 2b and 2c of Figure 2 also display the infectiousness curves (as functions of the signal strength and of the contact duration between individuals, see Supplementary Information A): even slight variations in the threshold used to implement the tracing policy may strongly influence the capacity to identify the contacts corresponding to the highest risks of infection.

Two additional policies (Table 6), inspecting close range but short exposure interactions and long range but long exposure interactions, are defined and tested in Supplementary Information C.5.

2.1 There is no containment without randomized testing

We first obtain an overview of how the control parameters impact the spread of the disease in an idealized model where ε_I, ε_T can take arbitrary values. In this way we can explore the full range of ε_I and ε_T and understand their effect – as in Ferretti et al.¹ – while later we can derive sets of feasible configurations that can happen in reality from the network simulations.

For each value of ε_I, ε_T, we use the model to predict the evolution of the number of new infected people λ(t) at time t up to a time T = 50 days, and we report the average growth or decline in the last 10 days. All numerical solutions of the continuous model reacg a stationary growth or decline regime (constant growth or decline rate of λ(t)). A negative number means that the epidemic is declining, while a positive one corresponds to growth (uncontained epidemics).

An important ingredient of the model is given by the probability s(τ)for an infected individual to be recognized as infected within a period of time τ, either via self reporting after the symptoms onset, or via randomized testing.²⁵ The ideal case in which all eventually infected people can be identified (s(τ) approaching 1 for large times) is reported in Figure 3a: this represents the best case scenario. We remark that this is the setting considered in the previous studies of this model.^1,3 Next, we assume instead that 40% of infected individuals are asymptomatic^1,31,32,58 and that only symptomatic individuals can be identified: no randomized testing is performed. We represent asymptomatics by considering that the probability of showing symptoms for infected people is a growing function of time that never reaches the value 1. In this case, the model predicts epidemic containment only if both ε_I and ε_T are very large, i.e., isolation and tracing of contacts are almost 100% effective (Figure 3b). Under this (realistic) assumption for the number of asymptomatic individuals, it is thus clear that essentially no epidemic containment can be obtained with only isolation and contact tracing policies: here, a randomized testing policy that increases the policy capability to detect infected people, beyond self reporting of symptomatic persons, is needed.²⁵ In the following, we thus assume that, in addition to the symptomatic individuals (whose distribution of identification times follows the definition of s(τ) in Supplementary Information A), 50% of asymptomatic infected are identified by a policy of randomized testing. In addition, we take into account a delay of 2 days between the detection of an infected individual and the time this information becomes available to the health authorities. This corresponds to a delay in the tracing and isolation interventions. The resulting predictions of the model are plotted in Figure 3c. This is our baseline for the following investigations.

• Download figure
• Open in new tab

Figure 3:

Growth or decrease rate of the number of newly infected individuals, assuming either that all the infected people can eventually be identified and isolated (Figure 3a); or that only symptomatic people can be isolated (Figure 3b, with 40% of infected individuals asymptomatic); or that symptomatic people can be isolated, and that an additional 50% of asymptomatic can be identified via randomized testing (Figure 3c), with a reporting delay of 2 days.

We also note that achieving the detection of 50% of asymptomatics by randomized testing is actually not the only viable strategy to achieve this baseline. Indeed, if such an effective randomized testing policy is not possible, we found that an essentially equivalent base scenario can be obtained if other mitigation policies (mandatory mask wearing, enhanced hygiene, cancellation of large gatherings, etc) are in place and reduce the reproduction number R₀ below a certain level (see Supplementary Information C.1).

2.2 Real data restrict the range of successful policies

We have run numerical simulations of the disease spread on the CNS dataset, implementing the different policies to determine their impact in mitigating the epidemic.

Figure 4 provides an illustration of the insights obtained by such simulations and the use of real contact data sets, by showing for Policy 5 and for ε_I = 0.8 the distribution of the time elapsed between an infection event and the successive contacts of the infected individual. Most contacts occur before infected individuals reach their largest infectiousness, but a non-negligible number of contacts occur as they are highly infectious.

• Download figure
• Open in new tab

Figure 4:

Distribution of the time elapsed between the infection of an individual and their successive contacts. The black line shows the normalized infectiousness ω(τ) as a function of time, and the purple line is the cumulative probability to detect an infected person s(τ). The plot is obtained with ε_I = 0.8 and for Policy 5 in the CNS dataset.

By considering the five different policies of Table 1 in terms of which contacts are considered at risk and thus kept by the app, and running corresponding simulations for ε_I = 0.2, 0.5, 0.8, 1, we can obtain in each case the actual value of ε_T that quantifies the quality of the tracing policy (see Section 4.1). This value therefore ceases to be an arbitrary parameter, but a direct consequence of the policy, the value of ε_I and the contact data. We can then plug the values (ε_I, ε_T) into the idealized model to simulate the spread of the epidemic, observe in which region of the diagrams of Figure 3 they fall, and deduce whether containment is achieved or not by this policy and this value of ε_I. The results, reported in Figure 5, clearly reveal that not all parameter configurations are reachable. In particular, the largest value of the tracing efficacy ε_T is possible only for Policies 4 and 5. Policies 2 and 3 still manage to reach the epidemic containment phase if ε_I is large enough, while Policy 1 is too restrictive in its definition of risky contacts and thus ineffective. We also note that Policies 4 and 5 do not differ in their results, although the number of contacts kept are quite different (as seen in Figure 2): once a certain amount of contacts is kept, keeping even more contacts (of lower duration or signal strength) does not improve the outcome.

• Download figure
• Open in new tab

Figure 5:

Growth or decrease rate of the number of newly infected people assuming that symptomatic people can be isolated and that an additional 50% of asymptomatic can be identified via randomized testing. The points correspond to the parameter pairs such that ε_I is an input and ε_T an output of the simulations on real contact data, for the policies of Table 1.

2.3 Any effective containment comes at a cost

Behind the scenes of the aggregated results of the previous section, there is a complex dynamic which merits further investigation. Indeed, the different tracing efficiencies that are observed are the macroscopic result of a different set of contacts considered as at risk. In some cases this produces the desirable effect of containing the spread, but side effects emerge as well. As mentioned in the introduction, indeed, some of the “at risk” contacts did not actually lead to a contagion event, while contacts classified as non risky might have, since the spreading process is inherently stochastic. It is thus important to quantify the ability of each policy to discriminate between contacts on which the disease spreads and the others, in terms of false positives (quarantined individuals who were not infected) and false negatives (non-quarantined infected individuals). To visualize this behavior, we focus on the case of ε_I = 0.8, since it is representative of a situation in which some policies are effective in containing the spread and others are ineffective (Figure 5): Figure 6 presents the corresponding time evolution of the average number of false negatives and of false positives for each policy.

• Download figure
• Open in new tab

Figure 6:

Temporal evolution of the numbers of false negatives (Figure 6a) and false positives (Figure 6b) for the five different policies, assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation (shading) over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been unnecessarily quarantined (false positives) over the whole simulation timeline.

What matters in terms of virus containment is to rapidly reduce the number of infected people that can have contacts and spread the virus. Independently of the policy, the curves of false negatives all peak after around 5 days, reaching similar levels. The curve drop to zero rapidly however only for the stricter policies, while for Policy 1 it remains at a high level for up to 15 days, corresponding to the fact that the spread is not contained early in the process.

The smaller number of false negatives for the effective policies comes however at the cost of a significantly increased number of false positives, as shown in Figure 6b. In other words, as a policy becomes more effective in tracing actually infected people, it also leads to the quarantine of individuals that have not been infected but that had a contact classified as risky by the tracing policy. In all cases, a peak of the number of false positives is reached after around 15 days, but this number is very sensitive to the specific policy, contrarily to the number of false negatives. In particular, it appears from the analysis of Section 2.2 that Policies 4 and 5 have a similar effectiveness to contain the epidemic and Figure 6 shows that they yield indeed similar numbers of false negatives, but their undesired side costs are different, as the broader definition of risky contacts of Policy 5 produces a larger number of false positives. This highlights once more the importance of fine-tuning of the chosen policy.

2.4 Low app adoption levels impair any containment effort

So far, we have assumed that the only limit to reach a perfect contact tracing resides in the technology specifications of each policy. This implies however that the totality of the population adopts the app, something which is clearly unrealistic in practice. We thus repeated our simulations assuming that only a fraction of the population uses the app, while the remaining individuals are outside the reach of the tracing and quarantining policies, but they are still isolated whenever detected because symptomatic or through random testing (see Supplementary Information 4.1.5).

We found that assuming an app adoption of 60% (Figure 7a) implies that no tracing policy is effective: None of the feasible tracing efficiency values of ε_T, obtained by simulations on the real contact network dataset, reach the threshold required to contain the spread. Quite similarly, an 80% app adoption (Figure 7b) can be sufficient to stop the epidemic only if Policy 4 or Policy 5 are adopted and a perfect tracing efficiency (ε_I = 1) is in place.

• Download figure
• Open in new tab

Figure 7:

Growth or decrease rate of the number of newly infected people, and real parameter pairs estimated from the network simulations for the policies of Table 1, assuming an app adoption level of 60% (Figure 7a) or 80% (Figure 7b), and an adoption of 80% with R₀ = 1.6 (Figure 7c).

In both cases, the effect of a limited app adoption on the tracing efficiency ε_T appears quadratic: a 60% app adoption reduces the efficiency roughly to its 35% percent, while an 80% adoption reduces it to the 60% percent (see Supplementary Information C.4). This effect is explained by the fact that to trace a contact between two individuals it is necessary that both have installed the app.

We further investigate a setting where we assume that, in addition to a 50% randomized testing policy, other measures are in place so that the reproduction number is reduced to R₀ = 1.6 (see Supplementary Information C.1 and Figure 7c. In this case, even an 80% adoption allows one to contain the contagion under a sufficiently strict digital tracing. Namely and remarkably, all the five policies are able to contain the virus if a perfect isolation (ε_T = 1) is in place. This scenario, however, is unrealistic, but it was not present in previous settings, and it highlights the fundamental benefit that a reduction of R₀ by other measures can bring to digital tracing. If instead the isolation efficiency is less than perfect, several policies manage to stop the contagion: if ε_I is at least 0.8, then Policies 2, 3, 4, and 5 are effective. Smaller values of ε_I are instead insufficient.

Figure 8a and Figure 8b offer an additional insight into the dynamics of the epidemic simulated on the contact network with an 80% app adoption, and reduced R₀ = 1.6. In particular, Figure 8a shows the evolution of the numbers of false negatives (active infected) and Figure 8b of false positives (susceptible quarantined), where each color represents the corresponding policy. The less restrictive policy (green line) does not yield a rapid containment; the number of false negatives does not decrease rapidly but remains large over almost 15 days. The decrease is faster for the more restrictive policies. The evolution of the number of false positives shows here an interesting pattern with a double wave, particularly marked in the more restrictive policy. This is due to the fact that when people leave the quarantine after the first peak, a large number of non-traced infected individuals are still free to have contacts. This implies a new wave of infections and necessary quarantines. In practice, as only a fraction of the population can be quarantined, they are likely to be quarantined multiple times.

• Download figure
• Open in new tab

Figure 8:

Temporal evolution of the numbers of false negatives (Figure 8a) and false positives (Figure 8b) for the five different policies, assuming an isolation efficiency of ε_I = 0.8, an 80% app adoption level, and a reduced R₀ = 1.6 with 50% testing of asymptomatics. The graphs depict the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been unnecessarily quarantined (false positives) over the whole simulation timeline.

3 Conclusions

In this study, we have analyzed the ability of digital tracing policies to contain the spread of Covid-19 outbreaks, using real interaction datasets to extract the main effective parameters and to shed light on the practical consequences of the implementation of various app policies.

We found that the set of parameters that allow containment of the spread is strongly restricted by the fraction of asymptomatic cases. By first assuming an ideal setting where any pair of parameters ε_I, ε_T is possible, we showed (Figure 3) that perfect contact and isolation policies are required if only symptomatic people can be detected and a realistic fraction of asymptomatic cases (40%) is assumed. We have thus assumed in addition that 50% of the asymptomatic can be detected by randomized testing (see Figure 5). We remark that this is in contrast with the scenario considered in Fraser et al.³ and in Ferretti et al.,¹ where all the infected population is eventually assumed to become symptomatic.

We tested five policies to define risky contacts that should be traced (Table 1), with different restriction levels. When implemented on real contact data measured by Bluetooth, they allow us to estimate, for each value of ε_I, the actual value of ε_T and thus to determine the efficacy of each policy (colored points in Figure 5). Using these implementations on real data restricts the available values of the control parameters and, as a consequence, only the most restrictive policies lead to epidemic containment.

Moreover, even for these policies, tracing is effective only if the isolation is effective: Policy 2 requires a perfectly effective isolation (ε_I = 1), while an 80% isolation is sufficient for Policies 3, 4, and 5 (Figure 5). In particular, better tracing policies may work with a less effective isolation strategy.

Our results highlight how isolation and tracing come at a price, and allow us to quantify this price using real data: the policies that are able to contain the pandemic have the drawback that healthy persons are unnecessarily quarantined (Figure 6). In other words, achieving a rapid containment and a low number of false negatives requires accepting a high number of false positives. This stresses the importance of a fine tuning of the tracing and isolation policies, in terms of the definition of what represents a risky contact, to contain the social cost of quarantines.

Finally, we have shown that an insufficient app adoption may render any digital tracing effort helpless on its own. In view of these results, bridging the gap between a realistic app adoption and the larger tracing capability required to contain the disease appears crucial. In particular, digital tracing in itself may not be enough if not complemented by a traditional manual tracing policy and/or other measures. This goal can be reached only with a joint effort of policy makers and health authorities in organizing an effective manual tracing, and of individual citizens in adopting the app.

It is also important to mention that our study comes with a number of limitations. First of all we are focusing on a single kind of intervention in order to fight the spread of the epidemics, which is just based on isolation and tracing. This is in order to isolate the effect of an app-based containment, avoiding additional spurious effects. In order to see the effect of isolation and tracing when implemented with other restrictive measures, we applied the same numerical machinery to a setting with a reduced R₀, representing a general reduction of the epidemic spread. We did not consider specific containment measures like social distancing, travel restrictions, school closures, and so on.

Moreover, we have considered data corresponding to a few limited social environments (a university campus, a high school and a workplace) and we cannot provide an overall general study that includes multiple and differentiated contexts and their mutual interplay. Our study is focused on the state of the art interaction datasets, which are nevertheless designed to capture a very limited social environment when compared e.g. with a real city. This limitation is then due to the lack of larger datasets (or synthetic social networks) involving people belonging to different environments, thus being able to represent the general interactions within the population of a city or a larger geographical area.

In addition, the implemented policies have been necessarily tailored to this specific DTU dataset, depending on the available values of RSSI supported by the used smartphones. Those might therefore differ in actual implementations currently under development, probably relying on a more advanced technology than that of 2014.

Finally, our study is limited by the state of the current knowledge of the contagion modalities of the COVID-19 virus, and in particular its dependence on physical distance among people and the duration of their contacts. The curve of infectiousness has been designed based on previous contagion studies and on reasonable assumptions. Should new insights emerge in the way the virus spreads, these could be easily incorporated into our model.

4 Data and Methods

The mathematical model we use includes several parameters characterizing the epidemic, and we define them following the most recent literature. Although this is a mere literature survey step, it is nevertheless of fundamental importance. Indeed, as we will see in the following, different assumptions at this level may lead to different predictions. The main parameters are:

• s(τ) which is the probability for an infected individual to be detected as infected (and thus isolated) within a time τ after infection, either via self reporting after the symptoms onset, or via randomized testing;

• β(τ), which is the infectiousness of an infected individual at time t after infection: this is defined as the probability that an individual who is infected since a period of time τ infects a new susceptible individual upon contact, ω(τ), multiplied by the reproduction number, R₀;

• β_data (τ, s, e), which is the analogous of β when applied to a real dataset: it depends on the duration e of a contact and on the strength s of the interaction, quantified by the strength of the signal exchanged by the devices registering the interaction.

Details on these choices are discussed in Supplementary Information A.

The realistic values for the parameters ε_I, ε_T and the interplay between the containment policies and the virus spread are estimated from real-world interaction datasets. Namely, we consider datasets describing networks of real contacts in a population, where interactions are determined by means of exchange of Bluetooth signals between smartphones. We develop a numerical simulation of the virus spread on this network, and in particular we implement a realistic notion of infection transmission upon contacts, which follows the parameters defined above. In this framework, we simulate isolation and tracing policies, where the tracing policy is implemented by defining sensors resolutions (e.g., a contact is detected if a minimal signal strength or a minimal contact duration are registered). It is also possible to model the rate of adoptions of the app, or the memory length of past traced contacts. The effect of these specifications on the actual effectiveness of the isolation and tracing policies are then obtained as output of the simulation: we obtain hence real-world estimations of the parameters ε_T, from the input value of ε_I (that encodes e.g. the testing capacity, or the effectiveness of tests). The details of this simulation, the definition of the policies, and the strategy used to estimate the control parameters are described in more detail in Section 4.1.

In order to incorporate these data-dependent and possibly time-varying control parameters into the predictions, we develop a finer analysis of the continuous model and its discretization. In particular, both Fraser et al.³ and Ferretti et al.¹ analyze the model prediction only in the limit of an infinite time horizon, and the first study³ furthermore assumes that the number of infected can only have an exponential behavior, either growing or declining. We instead consider the model at finite times and develop a new discretization of the continuous model that requires no assumptions on the functional form of the growth or decline of the contagion. This allows us to simulate more complex regimes and better quantify the effect of the control parameters, and in particular to align the model timescales with the simulation time, and thus to use the realistic parameters estimated from the simulations, including the implementation of time-dependent policies. This approach is presented in Supplementary Information B.

The overall output of the model is the predicted number λ(t) of newly infected individuals at time t, and we are interested to study policies that contain the epidemic, i.e., such that λ(t) → 0 as t grows.

Supplementary Information

B The continuous model and its discretization

The epidemic model form^1,3 (to which we refer for a precise derivation) provides a quantification of the number Y(t, τ, τ′) of people at time t that have been infected at time t − τ by people who have in turn been infected at time t − τ′.

The model characterizes Y as a function of s(τ) and β(τ) (see Section A in Supplementary Information). Observe that both are quantities in [0,1], and that s(τ) is a non decreasing. The model then states that Y(t, 0, t) is a given initial value and that for 0 < τ< t it holds

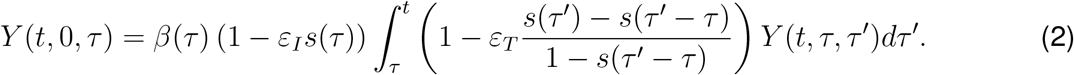
In the two cited papers the values of ε_I, ε_T ∊ [0,1] are fixed, while we assume from now on that they depend on τ.

Observe that in the absence of containment policies (i.e., ε_I = ε_T = 0) the model predicts a behavior i.e., the new infected people are just given by the cumulative number of people who have been infected at previous times, weighted by the infectiousness of the disease. In other words, every previously infected person is a possible agent of new infection, and in this scenario an exponential growth is observed. The isolation and tracing measures, on the other hand, act as discounts on the number of available spreader of the epidemic.

B.1 A more convenient form of the equations

As mentioned before, the model was analyzed in^1,3 by considering its asymptotic behavior as t grows to infinity. We instead need a finite-time model that allows a flexible treatment of real data. To this end, it is convenient to use the variable Λ(t,τ):= Y(t, 0, τ) (see³) which represents the number of people which are infected at time t by people who have been infected for time τ′ ≤ t.

With straightforward manipulations, equation (2) can be rewritten for 0 ≤ τ < t as follows where we changed the integration variable to ρ:= τ′ − τ, and we used the translational invariance of Y. In the variable Λ, this reads as

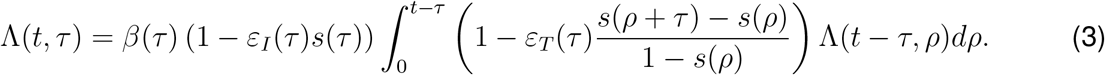
Observe that this is an evolution equation that requires to define an initial number of infected people, i.e., we assume that the quantity Λ (0, 0):= Λ₀ is a given number.

The quantity of interest is then the total number of newly infected people at time t.

B.2 Discretization

We fix a value T > 0 as the maximal simulation time and take n +1 points in [0, T] i.e., , 0 ≤ i ≤ n.

We will approximate the values of Λ(τ_k, τ_i) for k = 1,…, n and i = 0,…, k − 1, while, according to,³ we set A(T_k, T_i) = 0 for all i > k. Moreover, we assume that the value Λ(τ₁, τ₀) is given.

Observe that this discretization is equivalent to assume that the number of new cases is measured only at equal discrete times (e.g., at the end of each day) rather than measured continuously.

We show in the next section that the continuous model (3) can be approximated by defining a suitable value for Λ(τ₁, τ₀), and then iteratively computing the values of Λ(τ_k, τ_i) by applying the simple formula where the matrix is defined for 0 ≤ i, j ≤ n − 1 as

We remark that this equation is a forward-in-time system, meaning that the computations of the values of Λ(τ, t) is obtained using only values of A for previous time steps, which have thus already been computed. This is in strong opposition with the case of^1,3 where an eigenvalue equation has to be solved, and only the asymptotic state can be estimated.

Moreover, we can use Λ to compute

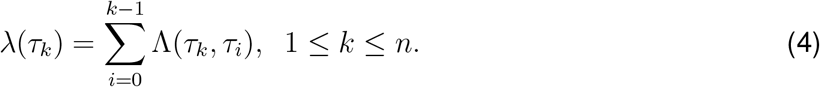
B.3 Derivation of the discretization

We fix a value T > 0 as the maximal simulation time and take n + 1 points in [0, T] i.e., , 0 ≤ i ≤ n.

The points will be used also to approximate integrals via a right-rectangle quadrature rule, i.e.,

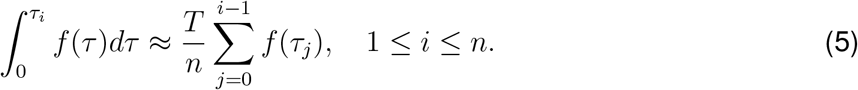
The goal is to approximate the values of Λ(τ_k, τ_i) for k = 1,…, n and i = 0,…, k − 1, while, according to,³ we set Λ(τ_k, τ_i) = 0 for all i ≥ k. Moreover, we assume that the value Λ(τ₁, τ₀) is given.

For 1 ≤ k ≤ n we first evaluate (3) at the points, first in the variable t for 1 ≤ k ≤ n, i.e., and then in the variable τ for τ < t, that is for 0 ≤ i ≤ k ≤ n, i.e.,

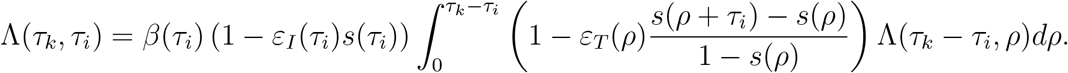
Now observe that for 0 ≤ i < k ≤ n we have which ranges between τ_k for i = 0 and τ₁ for i = k−1. The last equation becomes for 0 ≤ i ≤ k ≤ n

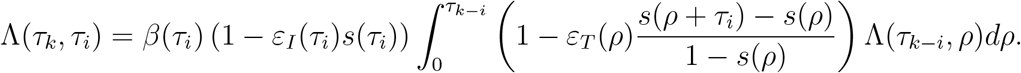
We can then use the quadrature rule (5) to discretize the integral and obtain

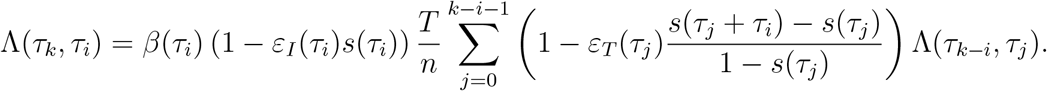
Observe that the upper limit in the sum has values 0 ≤ k − i − 1 ≤ k − 1 for 0 ≤ i< k. Moreover, in this case we have for 0 ≤ j ≤ k − i − 1 that which ranges between τ_i and τ_k−1. Inserting this into the last equation we get for 0 ≤ i < k ≤ n

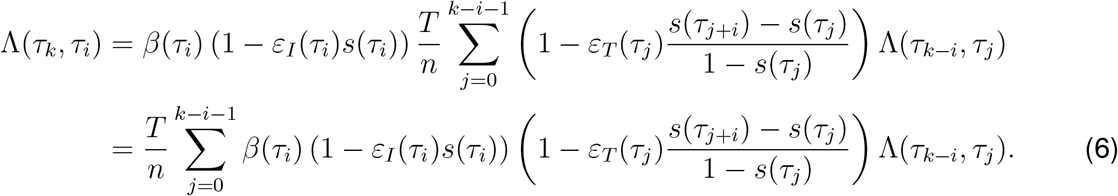
We can define the matrix whose entries are defined for 0 ≤ i, j ≤ n − 1 as which has a triangular structure (the first row is nonzero, in the second row the last element is zero, …, in the last row only the first element is nonzero).

With this matrix we can rewrite (6) as which is a recursive equation that determines the evolution of Λ(t, τ) once an initial condition is given.

Assuming for now that these initial conditions are given, we can compute Λ(τ_k, τ_i) forward in k and backward in i. That is, after we computed Λ(τ_ℓ, τ_i) for all ℓ = 1,…, k − 1, and for 0 ≤ i ≤ ℓ, we can use (7) to compute Λ(τ_k, τ_i) for 1 ≤ i < k, since in this case the right hand side contains values Λ(τ_k−i, τ_j) which have already been computed since 1 ≤ k − i ≤ k − 1 for 1 ≤ i < k.

The only remaining case is i = 0, and in this case the formula (7) gives instead thus where and thus

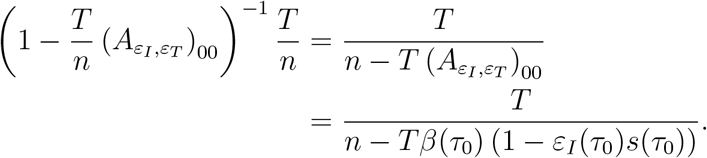
This term is positive if and only if

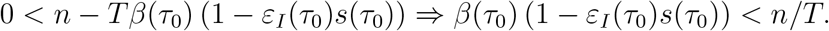
Since the left hand side is at most β(τ₀), it is sufficient to require that n/T > β(τ₀), or n > β(τ₀)·T.

In this way we defined Λ(τ_k, τ_i) for all values 1 ≤ k ≤ n and 0 ≤ i < k. It remains to assign the value Λ (τ₁, τ₀), which can be fixed to the initial value Λ₀.

C Evaluation of additional containment measures and refined policies

Some extensions are possible to our current setting, and we report the most relevant ones in the following. Each consists in additional steps to either enhance an existing policy or to replace it in order to investigate the effect of other important aspects of the tracing procedure.

C.1 Compensating a poor testing policy with a reduction of the reproduction number

As our base setting we assumed that the number of asymptomatics reaches 40%, and that 50% of them can be detected by a randomized testing policy. With these assumptions, the possible scenarios of the epidemic containment are depicted in Figure 3c.

We remark here that it is possible to reach a similar scenario without the need of randomized testing, provided other policies are in place. Namely, we found that assuming that other containment policies (such as masks, better hygiene, physical distancing) have the effect to reduce the reproduction number to R₀ = 1.6, and with no testing, the behavior of the epidemic spread is similar. We report the results of the model predictions and the network simulations for this scenario in Figure 9a, which indeed provides an outcome very similar to the one of our main simulation (see Figure 5).

• Download figure
• Open in new tab

Figure 9:

Growth or decrease rate of the number of newly infected people and efficiency of the containment policies assuming different scenarios: In Figure 9a only symptomatic people can be isolated, and a set of additional policies are in place so that the effective reproduction number is reduced to R₀ = 1.6; In Figure 9b, in addition to the basic setting, the app keeps track of 10 days (instead of 7 days) of past contacts.

C.2 Longer tracing memory

The robustness of the tracing policies is also of fundamental interest, and indeed we introduced (Table 1) five different policies that cover a wide range of possible sensitivity levels, both in space and in time.

It remains to explore how these policies depend on the memory length of the contact history, which is set to 7 days for all the policies (see Section 2). In particular, it is interesting to understand whether or not an increased memory would improve the effectiveness of each policy. We thus repeat the experiments assuming that the contacts of each individual are recorded for 10 days in the past, and report the results in Figure 9b. When compared with the original setting (see Figure 5), it is clear that the increased memory brings a negligible advantage (at the price of increased storage requirements). Indeed, the only visible improvement is a slight increase of the tracing effectiveness of Policy 4, which is now essentially equivalent to Policy 5.

C.3 Second order tracing

An additional possibility is to keep track of contacts in a recursive way. Namely, when an individual is isolated, not only its contacts are quarantined, but also its contacts’ contacts. This obviously means an enhanced risk in terms of preserving the privacy of individuals, and hence the major open question regarding this kind of policies is whether or not the increased intrusiveness into an individual’s social network provides a tangible improvement of the virus containment efforts.

A complete study of this scenario is beyond the scope of this paper for two reasons. First, the continuous model (see Section B) does not take into consideration this kind of tracing, and there is thus no way to use in a meaningful way any information provided by the study of the dataset. Second, although the datasets we consider are the state of the art in interaction monitoring, they are still rather small to study in a realistic way the effect of a policy that rapidly traces a very large number of persons.

Nevertheless, we find meaningful to report here a preliminary study of this additional, more intrusive tracing policy. The results are reported in Figure 10, where we show the time evolution of the number of false positives and false negatives (see Figure 6 for the analogous result in the standard setting). The plots show that, in the Copenhagen Study Dataset, the recursive tracing is sufficient to rapidly reduce to zero the number of false negatives (that is, the spread of the virus is stopped) with a number of false positives which is slightly lower than that obtained with the standard policies. Indeed, in this case the tracing is a very fast process (the maximum peak of quarantines is reached within 5 days after the beginning of the simulation), resulting in a massive quarantining. This considerably and rapidly reduces the amount of available susceptible individuals. As a consequence the active infected (false negatives) do not have enough contacts to infect and the spread is stopped. Basically, in this case the quarantines do not have the effect of isolating potential infected individuals but rather to reduce the number of susceptible individuals that could have a contact with potentially infected ones. As a result, almost all the individuals that we are quarantining are susceptible, i.e., we have a large amount of false positives and a negligible number of true positives (see Table in Fig.10). This result is in agreement with that obatined by Firth et al.⁴⁷ We remark once more that the reliability of this result is limited, being linked to a specific dataset and not to a general theory. Our insight is that the efficiency of the procedure is due to the finite dimension of the agent sample, where such an immediate and preventive intervention is sufficient to cut all the links between infected and susceptible, resulting in a situation which is more akin to a lock-down than to actual contact tracing.

• Download figure
• Open in new tab

Figure 10:

Temporal evolution of the numbers of false negative (Figure 10a) and false positive (Figure 10b) for the five different policies with second order tracing and assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been unnecessarily quarantined (false positives) over the whole simulation timeline.

Moreover, we should mention the fact that we did not consider the effect of a lower app adoption in this case, assuming that 100% of the population can be correctly traced. Such a scenario is even more unrealistic when considering second order tracing, being a large compliance obtainable only if privacy is perfectly preserved.⁴⁵

For these reasons we remark that the concept of second-order tracing, a topic of recent discussions, deserves further investigation and may possibly be expanded in a follow-up of this work.

C.4 Effect of a reduced app adoption

To complement the analysis of Section 2.4 on the effect of a limited app adoption, we provide here a numerical quantification of the reduction in the values of ε_T. For the five policies of Table 1 and for ε_I = 1, we report in Table 5 the ratio between the values of ε_T in the case of a limited appadoption (60% or 80%) and in the case of full app adoption (100%). Observe that the computed values are actually quite close to show a quadratic reduction effect, even if for most policies the reduction is actually slightly larger.

View this table:

• View inline
• View popup
• Download powerpoint

Table 5:

Ratio of the values of ε_T between a partial and a full app adoption, for the five policies of Table 1 and ε_I = 0.8. The values are rounded to the first decimal digit.

C.5 Close-range short-exposure vs long range long-exposure interactions

We test here two additional policies obtained by mixing a low space resolution and a high time resolution, and viceversa. The policies are defined in Table 6. Policy 6 has a signal strength of −70dBm and a duration of 10 minutes, resulting in a policy that captures short exposure but close range interactions. Policy 7 instead captures long exposure but long range interactions, having a threshold signal strength of −91dBm and a duration of 30 minutes.

View this table:

• View inline
• View popup
• Download powerpoint

Table 6:

Parameters defining the two additional policies.

Figure 11, in analogy with Figure 2, shows the new policies overlaid to the histograms of duration and signal strength of the CNS dataset contacts.

• Download figure
• Open in new tab

Figure 11:

Distribution of the duration (Figure 11c) and signal strength (taken as a proxy for proximity, Figure 11b) of the contacts in the CNS dataset. Figure 11a gives a scatterplot of signal strength vs duration, and displays the thresholds defining the two policies of Table 6.

The values of the parameters (ε_I, ε_T) characterizing the numerical simulations for the new policies are shown in Figure 12 (see Figure 5 for a comparison with the policies of Table 1), and it is clear that Policy 7 is as effective as the most restrictive policies (Policy 4 and Policy 5), while Policy 6 fails to contain the virus for any value of the isolation efficiency. The efficiency of quarantines is assessed by the number of false positives and false negatives, reported in Figure 13.

• Download figure
• Open in new tab

Figure 12:

Growth or decrease rate of the number of newly infected people assuming that symptomatic people can be isolated and that an additional 50% of asymptomatic cases can be identified via randomized testing. The points correspond to the parameter pairs such that ε_I is an input and ε_T an output of the simulations on real contact data, for the policies of Table 6.

• Download figure
• Open in new tab

Figure 13:

Temporal evolution of the numbers of false negatives (Figure 13a) and false positives (Figure 13b) for the policies of Table 6, assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation (shading) over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been unnecessarily quarantined (false positives) over the whole simulation timeline.

We deduce that the ability to control the contagion seems to be more sensitive to duration of contacts than to their spatial distance. Indeed, policies which capture close range but short exposure interactions happen to be less performative in quarantining people than those signaling long range interactions with long exposure. In other words, quarantining individuals who have had a short interaction with an infected one, even if at close-range, is unnecessary. On the other hand, it appears to be important to track contacts with a high spatial resolution, including the ones that happens at a rather long distance. If this is possible, there is no need to track short contacts, but it is sufficient to detect long ones

However, we remark once more that these results are depending on the infectiousness model that we have here defined, and that they could possibly change in a different setting.

Figures 14 and 15 refer to the more realistic case where the app adoption is reduced to 80% but the reproduction number R₀ is reduced too. We also maintain random testing in order to have the possibility of isolating asymptomatic individuals.

• Download figure
• Open in new tab

Figure 14:

Growth or decrease rate of the number of newly infected people assuming an 80% app adoption level, and a reduced R₀ = 1.6 with 50% testing of asymptomatics. The points correspond to the parameter pairs such that ε_I is an input and ε_T an output of the simulations on real contact data, for the policies of Table 6.

• Download figure
• Open in new tab

Figure 15:

Temporal evolution of the numbers of false negative (Figure 15a) and false positive (Figure 15b) for the policies of Table 6, assuming an isolation efficiency of ε_I = 0.8, an 80% app adoption level, and a reduced R₀ = 1.6 with 50% testing of asymptomatics. The graphs depict the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been unnecessarily quarantined (false positives) over the whole simulation timeline.

The case with second-order tracing for the two new policies is depicted in Figure 16, by showing false positives and false negatives in quarantines. Again, the effect of tracing is strong and immediate when having access to second order contacts, however the other side of the coin is represented by the fact that large part of the population is quarantined and almost all of the isolated individuals are not infected.

• Download figure
• Open in new tab

Figure 16:

Temporal evolution of the numbers of false negatives (Figure 16a) and false positives (Figure 16b) for the policies of Table 6 with second order tracing and assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been wrongly quarantined (false positives) over the whole simulation timeline.

• Download figure
• Open in new tab

Figure 17:

Distribution of the time since infection of the people having contacts, probability distribution ω(τ) (black line) determining the infectiousness as a function of time, and distribution s(τ) determining the cumulative probability to detect an infected person (purple line). The two plots are obtained with ε_I = 0.8 and Policy 5 for the InVS15 (Figure 17a) and the High_School13 datasets (Figure 17b).

• Download figure
• Open in new tab

Figure 18:

Growth or decrease rate of the number of newly infected people and efficiency of the policies for the InVS15 dataset (Figure 18a) and the High_School13 dataset (Figure 18b).

• Download figure
• Open in new tab

Figure 19:

Temporal evolution of the numbers of false negatives (Figure 19a) and false positives (Figure 19b) of the InVS15 dataset, for the five different policies and assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been wrongly quarantined (false positives) over the whole simulation timeline.

• Download figure
• Open in new tab

Figure 20:

Temporal evolution of the numbers of false negatives (Figure 20a) and false positives (Figure 20b) of the High_School13 dataset, for the five different policies and assuming an isolation efficiency of ε_I = 0.8. The graphs report the mean and standard deviation over 10 independent runs. The table reports mean and standard deviation of the total number of distinct individuals who have been quarantined and of those who have been wrongly quarantined (false positives) over the whole simulation timeline.