Abstract
We develop and apply a simplified SIR model to current data for the 2019-2020 SARS-Cov-2/Covid-19 pandemic for the United Kingdom (UK) and eight European countries: Norway, Sweden, Denmark, the Netherlands, France, Germany, Italy and Spain. The most important result of the model was the identification and segregation of pandemic characteristics into two distinct groups: those that are invariant across countries, and those that are highly variable. Amongst the former is the infective period TL, which was very similar for all countries, with an average value of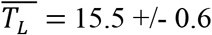 
days. The other invariants were TR, the average time between contacts and R = NC, the average number of contacts while infective. We find 
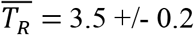days and 
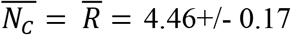. In contrast to these invariants, there was a highly variable time lag TD between the peak in the daily number of infected individuals and the peak in the daily number of deaths, ranging from a low of TD = 4 days for Italy and Denmark, to a high of TD = 17 for Norway. The mortality probability among identified cases was also highly variable, ranging from low values 3.5%, 5% and 5% for Norway, Denmark and Germany respectively to high values of 18%, 18% and 20% for France, Sweden and the UK respectively. Our analysis predicts that the number of deaths per million population until the pandemic ends (defined as when the daily number of deaths is less than 5) will be lowest for Norway (45 deaths/million) and highest for the United Kingdom (628 deaths/million). Finally, we observe a small but detectable effect of average temperature on the probability α of infection in each contact, with higher temperatures associated with lower infectivity.
Introduction
Coronaviruses are large, enveloped, single-stranded RNA viruses which are widespread in animals and usually cause only mild respiratory illnesses in humans [1-4]. However, in 2003, a new coronavirus, SARS-CoV emerged which caused a life-threatening respiratory disease, with a fatality rate of almost 10% [5,6]. Unfortunately, after an initial burst of interest in development of treatment options, interest in this virus waned. The emergence of a novel coronavirus SARS-CoV-2, identified in January 2020 as the likely causative agent of a cluster of pneumonia cases which first appeared in Wuhan, China in December 2019, has since caused a worldwide pandemic [7]. SARS-CoV-2, is the seventh known coronavirus to cause pathology in humans [1]. The associated respiratory illness, called COVID-19, ranges in severity from a symptomless infection [8], to common-cold like symptoms, to viral pneumonia, organ failure, neurological complications and death [9,10]. While the mortality in SARS-CoV-2 infections appears to be lower than in SARS-CoV [1, 9,11], this new virus has more favorable transmission characteristics, such as a higher reproduction number [12], and possibly, a long latency period and asymptomatic infective phase.
The governments of several countries have taken significant measures to slow down the infection rate of Covid-19, such as social distancing, quarantine, identification, tracking and isolation. However, there is no uniform policy, some governments reacted later than others and some (e.g. Sweden) made a deliberate decision to keep the country open, leaving counter-measures up to individual residents.
A large amount of consistent public data is now available on the number of tests performed, the number of infected cases and the number of deaths from several countries. Although tests are never 100% reliable, when the number of tests exceeds the identified cases by factors of four or higher, the data are likely to be fairly reliable. This is true for several countries in Europe.
The Model
We model the Covid-19 pandemic by a simplified version of the SIR model [13], which partitions the population into three compartments, Susceptibles (S), Infectious (I) and Removed (R: Recovered or Dead, after being infected). This and other models to study the global spread of diseases have been used in a variety of contexts (For some recent reviews, see [14,15,16]).
So far, the Covid-19 pandemic, at least in the developed countries in Europe where we will apply this model, seems to have the following dynamics: After being infected, an individual remains able to infect others for an average of TL days. After a time TL, the infected individual becomes sick, gets tested, is identified as infected and is removed from the pool by quarantine or hospitalization. Thus, in our context, the SIR model dynamics can be defined as follows: At t=0, from a pool of N interacting individuals, almost all are in the S compartment, except for a few; viz, those that are infected and able to infect others but not yet removed. These are in the I compartment. The R compartment is empty at t=0. Over time, individuals move from S to I and from I to R. In R, they either recover or die. Since the R compartment is populated only from the I compartment, on average, the number removed each day must equal the number infected at a corresponding day in the past; i.e. the two are related by a fixed time displacement. We assume that the number dead and recovered each day are proportional to the number removed each day by fixed probabilities, that remain invariant over the course of the epidemic. We’ll have more to say about that below. For the moment we note that the above implies that the number dead each day is proportional to the number infected on some previous day, as is the number recovered, though generally with a different time delay.
We start with a well-mixed pool of N interacting individuals and define,
A fraction δ of the infected individuals will die after being identified as infected. On average, there will be a time delay TD between when a person is identified to be infected (tests positive) and when he/she dies of the disease. TD will depend on a variety of factors, such as quality of care, age, severity of disease, co-morbidities, immune status etc.
Then the number of deaths at time t will be:
Let,
and
The equations governing the dynamics are then:
The initial conditions at t = 0 are:
An equation relating the state variables X1 and X2 can be obtained by dividing (8) by (9) and integrating. This gives,
Hence,
Substituting this into (13) gives:
At t = ∞,X2 = 0. Hence, from (12), we get:
is the fraction of susceptible individuals at t = ∞.
When S1(∞) → 1, log(S1(∞)) ~ − (1 − S1→(∞)) and R → 1
When nobody is infected, there is no pandemic and S1(∞) = 1, which corresponds to R = 1.
It is easy to show that if R < 1, there are no solutions to (16) that satisfy 0 ≤ S1(∞) ≤ 1.
Fitting the Model to data
The data that is available is:
and
These are related by:
and,
It is worth noting that the dynamics of the number removed each day and the total number of removed do not enter our analysis explicitly. Some context with the full SIR model can, however, be provided by noting that the total number of removed individuals increases asymptotically at large times to N(1 − S1(∞)).
The challenge is to determine N, α, γ = 1/TL, R, δ, TD from these data, using (5), (8), (9) to do numerical fits. δ, TD can be easily determined by scaling and shifting X2(t) and X4(t); i. e. they are obtained directly from the data, and don’t require fitting the solutions to differential equations. Of the four remaining parameters, N, α, γ, R, only 3 are independent. We choose these to be N, γ, and R. Consequently, we proceed as follows:
Using (12), we define α in terms of N, γ, R. This eliminates α.
Estimating P = maximum value of X2(t) from the data, we determine N in terms of R using (15). This eliminates N.
γ(R − 1) is determined as the coefficient of t in the exponential rise of X2(t) for small t (see Appendix A). This eliminates γ.
Using a numerical solver, we vary R to fit the observed data for X2(t).
Note that once N, α, γ, R are determined, (16) determines 
, the fraction of the pool of interacting individuals who are NOT infected at the end of the pandemic.
Some other useful parameters we can measure from the analysis are:
Data and Fitting Methodology
Data for the number of cases and deaths was obtained from https://ourworldindata.org/coronavirus-source-data, and data for the number of tests was obtained from https://ourworldindata.org/coronavirus-testing. The data for each country was considered accurate only if the number of tests done per day per identified case was greater than three for each day. The values of X2(t) and X4(t) were extracted from the data for the cumulative number of cases and the cumulative number of deaths
The following procedure was used to obtain the parameters by fitting the solutions of 8 and 9 to the data. For each choice of parameter values, starting at a value t0 of t such that X2(t0) = a ≥ 10, the Matlab Solver myode2 was used to numerically determine [X1(t), X2(t)] as a function of time using the initial condition, [X1(t0) = N − α, X2(t0) = a]. The solutions were then compared to the actual data. To determine an error on the fitted parameters, N and R were varied until a range of parameter values was found that fitted the data for X2(t) including fluctuations. Using the average value of the fitted parameters, δ and TD (see (5)) were estimated by shifting and scaling the fitted values of X2(t) from the solver and comparing them to the actual values of X4(t) from the data. Using the mean values for the parameters, the solver fits for [X1(t), X2(t)] were extended beyond the last date for which the data was available to estimate the date when the number of daily deaths would be less than 5. This day was declared to be the date when the pandemic would end. The fitted solutions [X2(t), X4(t)] were also used to estimate the total number of cases and the total number of deaths. Finally, the values of TL and TR were determined from the fitted data using (21) and (22) respectively.
Results and Discussion
In this paper, we focus on four North European (N-Eu) countries, Norway, Sweden, Denmark and the Netherlands, four South European (S-Eu) countries, France, Italy, Spain and Germany, and the United Kingdom (UK). The first date for which data was available was 12/31/2019, which we denote as day number 0 in the plots to follow. Among the countries considered here, the earliest cases were identified in France, on 1/25/2020, which corresponds to day 25. In the other countries, the earliest case was identified on the following days, counting from 12/31/2019: Netherlands: day 59, Denmark: day 58, Sweden: day 32, Norway: day 58, UK: day 31, Spain: day 32, Germany: day 28, Italy: day 31.
Adequate testing was done so that the data on the number of positive cases is reliable
Whereas deaths are unambiguous, the data for the number of cases is trustworthy only when a sufficient number of tests are performed. Figure 1a and 1b show the cumulative number of tests performed in the countries analyzed starting from 12/31/2019. We see that in the N-Eu countries, the ratio of the cumulative tests to cumulative cases always exceeded five, whereas in the S-Eu countries, this ratio always exceeded three. Consequently, we expect that the reported number of cases is reliable.
The values of N, α, γ, R, δ, TL, TR,TD
Using the methodology described above, we computed N, α, γ, R, δ, TL, TR, TD. These results are summarized in Table I. Figures (2) and (3) show the data and fits of our model for X2, the number of daily cases for the N-Eu countries and UK and the S-Eu countries respectively. Similarly, Figures (4) and (5) show the data and fits for the number of daily deaths X4 for the N-Eu countries and the US and S-Eu countries respectively. We see that whereas for most countries, the fits of the model to the data for X2 (Figures 2,3) are quite good past the peak, for Sweden, Denmark and the UK, there is a plateau in the data after the peak, suggesting that sufficient social-distancing/quarantine/containment measures were not successful or not implemented in these countries, especially before and after the peak, when the fraction of infected cases would be high and some fraction of these may be asymptomatic and so able to infect others. This means that our final estimates (Table I) for the number of cases and deaths and times for when the pandemic will end for these countries may be on the conservative side.
Observed data (blue circles) for the number of cases per day (X2(t)) and fits (solid lines) obtained by solving (8) and (9) using the ODE solver ode45 in Matlab. The mean values of the parameters obtained (inset) are from the solid black line and the error bars are from the two red lines. The method used for the fits was to find γ(R − 1) from the exponential rise in X2 for small t (Appendix A), estimate the peak value P of X2 (which gives the value of N using (15)) and then vary R to obtain good fits to the data.
For X4, there is only a hint of a plateau past the peak for Spain but not for the other countries.
Predictions for the end of the pandemic, total cases and deaths
If we define the end of this particular pandemic as the date when the number of deaths in a single day will be less than 5, then the predicted dates from Table I and Figures 3, 5 are: Netherlands: 6/11/2020, Denmark: 4/30/2020, Sweden: 6/12/2020, Norway: 4/15/2020, UK: 8/3/2020, Spain: 6/19/2020, Germany: 6/6/2020, France: 6/23/2020, Italy: 7/17/2020.
Observed data (red circles) for the number of deaths per day (X4(t)) for N-Eu countries and fits (solid lines). The fits were obtained by merely the fits from Figure 2 for X2 (t) forward in time by an amount TD and scaling the results by the value δ (see (5)).
Observed data (blue circles) for the number of cases per day (X2 (t)) and fits (solid lines) obtained by solving (8) and (9) using the ODE solver ode45 in Matlab. The mean values of the parameters obtained (inset) are from the solid black line and the error bars are from the two red lines. The method used for the fits was to find γ(R − 1) from the exponential rise in X2 for small t (Appendix A), estimate the peak value P of X2 (which gives the value of N using (15)) and then vary R to obtain good fits to the data.
Observed data (red circles) for the number of deaths per day (X4(t)) for UK and S-Eu countries and fits (solid lines). The fits were obtained by shifting the solver fits from Figure 4 for X2 (t) forward in time by an amount TD and scaling the results by the value δ (see (5).
The projected number of cases per million population and the projected number of deaths per million population until the dates above are shown in Figure 6a and 6b. We expect that Norway will have the smallest number of cases per million population and Spain the highest. The number of deaths per million population will be smallest in Norway and highest in Italy and the UK.
We define the end of the pandemic as the day when the number of deaths is less than 5 per day. a) Projected number of cases per million population when the pandemic ends and (b) Projected number of deaths per million population when the pandemic ends. (c) Demonstration of a possible temperature effect on the infectivity parameter α. The scale of the x-axis is temperature and the plotted values are the mean temperatures in February of the principal cities of the countries studied. The results suggest that the infectivity of SARS-CoV-2 decreases with increasing temperature. (d) The fraction of infected who died and (e) The average number of days from identification of disease to death (see (5)).
Among the three countries with the highest number of cases and deaths per million population (Spain, Italy and the UK), Spain seems to have done well in containment; in spite of the highest number of cases per million, Spain will have the fewest deaths per million among these three countries. On the other hand, the UK seems to have done rather poorly, with the lowest number of cases per million but the highest number of deaths per million.
SARS-Cov-2 may transmit less effectively at higher temperatures
An interesting observation is a “Temperature Effect” on the value of the infectivity parameter α, as shown in Figure 6c. The scale on the x-axis is the average temperature in February 2020 for the principal cities. The higher the temperature, the lower is the value of α. This suggests that the SARS-Cov-2 may transmit less efficiently at higher temperatures.
The death probability δ, the infective period TL, and the time interval TR between contacts while infective
The fraction δ of identified cases who die after a time interval TD (Table I and Figure 6d) also shows significant variation by country, with Norway, Germany and Denmark having the smallest values: δ = 0.035,0.045 and 0.050 respectively, and UK, France and Sweden the highest: δ = 0.20,0.19 and 0.18 respectively. Assuming that most of the deaths occurred in hospitals, the average time TD from to infection to death was highest (15 days) for Norway and lowest (4 days) for Denmark and Italy (Figure 6e, Table I).
Although the time delay differs for each country, it is also true that for every country, the relation between the removed population and the infected population is time invariant. This is not required a priori. For example, pressure on resources during a peak period of infectivity could cause a transient increase in the number of deaths per day relative to the number of recovered per day. In such a situation, a single probability δ need not suffice for the entire epidemic. The fact that there is little evidence of this to within the quality of the data suggests that the effectiveness of life saving measures appears to be relatively insensitive to changes in the infective burden.
The time interval TL = 1/λ during which an infected person is able to infect others was quite uniform across all the countries with the average value: E(TL) = 15.5 +/- 0.6 days.
The time interval, TR between contacts between a susceptible and infective individual was also remarkably uniform for all countries, with the average value: E(TR) = 3.5 +/- 0.2 days.
Finally, the average number of contacts while infective or 
, which is also the value of R, varied only in a narrow range for all countries, averaging: E(NC) = E(R) = 4.46+/- 0.17.
S1(∞), herd immunity and estimating the naive fraction
How do we interpret N? It is certainly not the total population, because the model assumes complete mixing and the entire population does not interact all at once. In a compartment model such as this one, N is most likely the compartment size. Indeed, if everyone infected is immediately quarantined, then N = 1. If people were to be isolated in groups of size 100, then N=100. Hence, a reasonable interpretation of N is that it is the effective size of the population of susceptible individuals who interacted to give rise to observed number that were infected. The “naive” or uninfected fraction of this population at the end of the pandemic is given by S1(∞). Because of the high value of R, S1(∞) is small for all countries (Figure 7a). This means that, by the time the pandemic ends, herd immunity will have been established among the subset of the population that interacted with those who were identified to be infected. The highest “naive” fractions among this group were 5%, 3% in Norway and Denmark respectively and the lowest were 0.4%, 0.7% in Sweden and the UK, which would suggest that herd immunity will be highest in the latter two countries.
(a) The fraction S1(∞) of the N susceptible individuals who are uninfected at the end of the pandemic. Note that the small values shown do not suggest that herd immunity was established for the whole population. This is because N does not represent the whole population but rather the subset of individuals exposed to those who were infected. (b) An estimate of the number of people in each country who would need to be tested after the current pandemic ends to identify the naive population to an accuracy of 5%. In making the estimate we have used the error bars shown in Figure 7a.
The important question is whether or not the results in Figure 6f mean that herd immunity has been established in the larger population. Since the size of the unidentified infected pool able to infect others is unknown, it is difficult to determine whether the small N values relative to the population size mean that a large fraction of the population will remain naive at the end of the pandemic. However, one possible explanation of the observation that in several countries (Sweden, UK, Denmark), the model results deviate past the peak from the observed data might be that it reflects exposure of a larger pool of susceptible individuals to those infected before the peak because of the lack of social distancing or early lifting of quarantine in these countries.
The determination of the true naive fraction at the end of the pandemic can only be done by random testing post-hoc. However, we can use the results of Figure 7a to estimate how many people would need to be tested to achieve a given accuracy, if indeed the naive fraction in the whole population is as shown in this Figure. We note that the errors on S1(ot) in Figure7a are approximately 50% of each value. This means that to estimate the naive fraction to an accuracy of x% one would need to test a fraction 
of the population, where NP is the population size of the country and N is the size of the susceptible pool in our model. Using the data in Table I for N, NP, to test whether the population naive fraction is the same as in Figure 7a to an accuracy of 5% the random testing needed for each country ranges from a minimum of 61 thousand tests for Norway and a maximum of 1.61 Million tests for Spain. (Figure 7b).
A comparison of cases and deaths among the countries
A direct comparison of the cases and deaths among these none countries can be made by plotting the normalized fractions S2(t) = X2(t)/N and S4(t) = X4(t)/N on the same scale (Figures 8,9), with the parameter N obtained from the fits described above. These results show that:
Among the N-Eu countries, although the pandemic started at about the same time, the initial normalized case growth rates in Norway and Sweden were higher (Figure 8a), because of the higher value of α discussed previously (Figure 6c).
In all countries other than Sweden and the UK, S2(t) is decreasing after reaching a peak. However, in Sweden and the US, it has merely plateaued (Figures 8a, 9a), suggesting that our predictions for the total number of cases in these countries (Table I) are likely to be significantly underestimated. In Sweden and to some extent also in the UK, S4(t) is not declining after reaching a maximum value (Figure 8b, 9b), suggesting that our estimates for the total number of deaths in these countries may also be significant underestimates.
In the S-Eu countries and UK, the pandemic began first in Italy and last in the UK (Figure 9a). The peaks in cases in all the S-EU countries happened at about the same time with similar values for S2 (t) at the peak. However, in the UK, there was no peak in S2 (t) but rather a plateau, as in Sweden.
In spite of similar normalized cases S2(t) for all countries, Germany and Norway had the smallest normalized deaths S4(t).
The peaks in S4(t) happened at significantly different times for the nine countries investigated (Figure 8b, Figure 9b), verifying the differences in TD, the time delay between identification of disease and death (Table I), which was shortest for Italy and Denmark (4 days) and highest for Norway (17 days).
Data Availability
The data used in this paper were all derived from public sources. Links to these data are included in the paper. The Matlab codes used to analyze the data along with all data files will be provided on request - email: gyanbhanot{at}gmail.com.
Summary
We have developed a simple model for the evolution of the Covid-19 pandemic that makes several useful predictions. These methods can be easily applied to other countries around the world if accurate data on the number of tests, the number of identified cases and the number of deaths is available.
Author Contributions
GB: Idea development, analysis, manuscript.
CD: Idea development, analysis, manuscript.
Declaration of Interests
The authors declare no conflict of interests
Declaration regarding data and software
The data used in this paper were all derived from public sources. Links to these data are included in the paper. The Matlab codes used to analyze the data along with all data files will be provided on request - email: gyanbhanot{at}gmail.com.
Table I Legend:
Table showing results from the fits for all 9 countries.
Funding and Acknowledgments
GB was partly supported by grants from M2GEN/ORIEN, DoD/ KRCP (KC180159) and NIH/NCI (1R01CA243547-01A1). He thanks Professors Pablo Tamayo and Jill Mesirov for their kind hospitality at UC San Diego during his sabbatical year 2019-2020 when this work was done.
Footnotes
Gyan Bhanot, PhD, 136 Frelinghuysen Road, Busch Campus, Rutgers University, Piscataway, NJ 08854, USA, Phone: (848) 391-7508, Fax: (732) 235-5331, Email: gyanbhanot{at}gmail.com
Charles DeLisi, PhD, 24 Cummington Mall, Boston University, Boston, Ma 02215, Phone 617 875 5138, Email: DeLisi{at}bu.edu
