Abstract
Aims We aimed to determine the effectiveness of surveillance using testing for SARS-CoV-2 to identify an outbreak arising from a single case of border control failure at a country level.
Methods A stochastic version of the SEIR model CovidSIM v1.1 designed specifically for COVID-19 was utilised. It was seeded with New Zealand (NZ) population data and relevant parameters sourced from the NZ and international literature.
Results For what we regard as the most plausible scenario with an effective reproduction number of 2.0, the results suggest that 95% of outbreaks from a single imported case would be detected in the period up to day 33 after introduction. At the time point of detection, there would be a median number of 6 infected cases in the community (95%UI: 1–68). To achieve this level of detection, an on-going programme of 7,800 tests per million people per week for the NZ population would be required. The vast majority of this testing (96%) would be of symptomatic cases in primary care settings and the rest in hospitals. Despite the large number of tests required, there are plausible strategies to enhance testing yield and cost-effectiveness eg, (i) adjusting the eligibility criteria via symptom profiles; (ii) and pooling of test samples.
Conclusions This model-based analysis suggests that a surveillance system with a very high level of routine testing is probably required to detect an emerging or re-emerging SARS-CoV-2 outbreak within one month of a border control failure in a nation.
Introduction
One of the challenges with a new pandemic such as COVID-19, is how best to undertake surveillance. Good quality surveillance is needed to maximise rapid disease control eg, with case isolation and contact tracing to identify further cases and to quarantine contacts. This capacity is particularly critical for nations that decide to contain spread at an early stage and even eliminate transmission entirely (eg, as New Zealand has planned [1] and Australia has as a potential option [2]). In particular it may be relevant to the following groupings of island jurisdictions (as per WHO data on 5 May 2020 [3]):
Those jurisdictions which have avoided any COVID-19 cases to date (eg, via border controls), but which are still at risk if border controls fail. These mainly include island jurisdictions in the Pacific Ocean (eg, American Samoa, Cook Islands, Federated States of Micronesia, Kiribati, Marshall Islands, Nauru, Niue, Palau, Samoa, Solomon Islands, Tokelau, Tonga, Tuvalu, Vanuatu, and Wallis and Futuna).
Those jurisdictions which have only experienced sporadic cases and may have successfully contained spread. These are mainly Caribbean islands (eg, Trinidad and Tobago) but also include some islands in the Pacific (eg, Fiji).
Those jurisdictions which have had larger outbreaks of COVID-19, but have instituted tight border controls and have declining numbers of new cases. These settings may therefore be on track towards eliminating the virus (eg, Australia, New Zealand and Taiwan).
A recent Australian study [4], suggested that timely detection and management of community transmission of COVID-19 is feasible. This modelling study concluded that “testing for infection in primary care patients presenting with cough and fever is an efficient, effective and feasible strategy for the detection and elimination of transmission chains”. For example, when testing 9000 people per week (per million population), the authors estimated that no cases of COVID-19 would be missed in some circumstances. This type of surveillance could therefore be relevant to identifying emergent or re-emergent SARS-CoV-2, the pandemic virus causing COVID-19.
Given this background, we aimed to determine the effectiveness of surveillance using testing for the SARS-CoV-2 virus to identify an outbreak arising from a single case of border control failure in a nation without it.
Methods
To run pandemic spread scenarios for New Zealand, we used a stochastic SEIR type model with key compartments for: susceptible [S], exposed [E], infected [I], and recovered/removed [R]. The model is a stochastic version of CovidSIM which was developed specifically for COVID-19 by two of the authors (http://covidsim.eu; version 1.1). Work has been published from version 1.0 of the deterministic version of the model [5] [6], but in the Appendix we provide updated parameters and differential equations for version 1.1. The stochastic model was built in Pascal and 100,000 simulations were run for each set of parameter values.
The parameters were based on available publications and best estimates used in the published modelling work on COVID-19 (as known to us on 6 May 2020). Key components were: a single undetected infected case arriving in New Zealand via a border control failure, 80% of infected COVID-19 cases being symptomatic, 39.5% of cases seeking a medical consultation in primary care settings, and 4% of symptomatic cases being hospitalised (see Table A1 in the Appendix for further details). We assumed that the initial undetected case could be at any stage of infection – to cover both failures of managing quarantine at the border, but also failures around the management of non-quarantined workers such as air-crew and ship-crew. Scenarios considered different levels of transmission with the effective reproduction number (Re) of SARS-CoV-2 to be 1.5, 2.0, 2.5 and 3.0 (Table A1). Other scenarios considered the impact of 75% of symptomatic people seeking a medical consultation (eg, as the result of a potential media campaign); and another considered a possible school outbreak (eg, a border control failure involving a teacher or student returning from overseas). The assumptions for the latter involved: Re = 2.0, only 5% of symptomatic cases seek medical consultation, and only 0.5% being hospitalised.
For the detection of COVID-19 cases, we assume testing of 95% of cases of symptomatic cases of respiratory illness seeking medical attention in primary care and of hospitalised cases of respiratory illness. For parameterising the size of these two groups, we used official statistics and results from the Flutracking surveillance system used in New Zealand (Table A1). The sensitivity of the PCR diagnostic test (at 89%) was based on a meta-analysis (Table A1).
Results
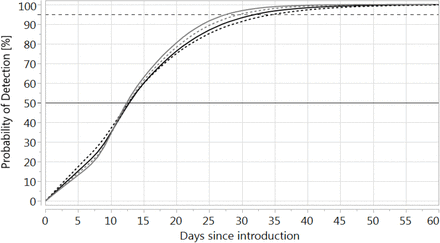
For what we regard as the most plausible scenario with an Re of 2.0 (ie, where people are practicing some level of reduced social contact because of the pandemic in other countries), the results suggest that 50% of outbreaks from a single imported case would be detected in the period up to day 13 and 95% in the period up to day 33 (Table 1, Figure 1). At the time of detection (to day 33), there was an estimated median number of 6 infected cases in the community (95% uncertainty interval [UI]: 1− 68). Similarly, for this same period, we expected that 4.7 primary care consultations and 0.5 hospitalisations of COVID-19 patients will have occurred. To achieve this level of detection, an on-going programme of 5,600 tests per day would be required, which is 7,800 tests per million people per week for the whole New Zealand population. This is one test per 128 individuals per week when combining the testing of the 39.5% seeking medical attention for cough and fever symptoms and the testing of those being hospitalised for respiratory conditions. The vast majority of this testing (96%) would however, be in primary care settings and the rest in hospitals.
For all scenarios, 95% of outbreaks were detected before five weeks after introduction. The highest value (32 days) was for the simulated school outbreak where medical consultations were assumed to be much less likely (due to symptoms in young people being typically milder). Increasing the extent by which symptomatic people seek medical consultations to the 75% level (up from that reported by Flutracking at 39.5%), would reduce the time to detection (eg, from 33 to 23 days for the Re = 2.0 scenario at the 95% probability level, Table 1).
Probability of COVID-19 case detection after reintroduction of the infection (the different curves represent the results of 100,000 simulations each, using Re = 1.5 (black dotted), 2.0 (black solid), 2.5 (grey dotted), and 3 (grey solid), respectively.
Discussion
This analysis indicates the challenges for a surveillance system designed to detect the emergence or re-emergence of SARS-CoV-2 transmission in a nation with border controls. A very high level of testing is typically required in primary care settings and hospitals to detect an outbreak arising from a single border control failure.
This testing level, at 7,800 per week per million population, is somewhat higher than the levels in NZ in early May 2020 (ie, the 7-day rolling average at this time was around 4,200 tests per day [7], which is around 6000 people per week per million population, although this included some screening of asymptomatic people). Also achieving this high level of testing would require maintaining public support and participation with testing in an environment where border control failures might be considered to be rare events (though even a 14-day quarantine period for arriving travellers is likely to have a small failure rate [8]).
Despite the high level of testing required for this type of surveillance system, there are potential ways that might improve the yield and cost-effectiveness of such testing:
Further refining eligibility criteria for testing in the primary care setting (eg, rather than just cough and fever). This could improve both the sensitivity and specificity of the surveillance system (eg, patients with self-reported olfactory and taste disorders had high specificity as a screening criterion in a Singapore study [9]). While PCR tests typically have very high specificity, the test kits with the best characteristics could be evaluated for cost-effectiveness.
Pooling samples for PCR testing may preserve reagents and be more cost-effective [10], but would need to be balanced against potential loss of sensitivity and associated diagnostic delays.
Furthermore, extremely comprehensive testing of all hospitalised cases with respiratory symptoms has some other advantages. It assists with appropriate diagnosis and management of COVID-19 cases when these are identified, but it also may protect against a hospital outbreak of COVID-19 which could endanger lives of inpatients and put many health workers into quarantine.
Study strengths and limitations
This is the first such modelling analysis for a country with an elimination goal for COVID-19. Nevertheless, this work could have been refined further by a focus on a narrower range of acute respiratory diseases (eg, excluding the category of hospital admissions for chronic lower respiratory diseases (ICD10 codes: J40-J47). But since hospital admissions for these often involve an acute aspect eg, acute bronchitis on top of chronic obstructive respiratory disease, we took the parsimonious approach of considering all respiratory diseases.
This analysis also did not explore other surveillance options such as routine active surveillance of specific groups (eg, air-crew, ship-crew and port workers), or the testing of town and city sewerage systems for the virus, as is being explored in several jurisdictions internationally [11] [12]. Yet these surveillance issues should also be considered by nations that aim to keep the COVID-19 pandemic out or eliminate it.
Conclusions
In conclusion, this model-based analysis suggests that a surveillance system with a very high level of routine testing is probably required to detect an emerging or re-emerging SARS-CoV-2 outbreak within one month of a border control failure in a nation. But further work is required to improve on this type of analysis and to evaluate other potential surveillance system components.
Data Availability
Simulation results are available on request to the authors
Funding
Dr Schwehm is supported by the University of Tübingen and the IMAAC-NEXT Association. Professor Wilson is supported by the New Zealand Health Research Council and Ministry of Business Innovation and Employment (MBIE) funding of the BODE3 Programme. However, these organisations had no role in the decision to perform this study, in its content, or the decision to publish.
Competing interests
The authors have no competing interests.
Appendix: Mathematical description of the CovidSIM model (version 1.1) and model parameters
The stochastic simulations are based on the following differential equations:
Model dynamics
Number of susceptible individuals 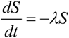

Derived variables
Total number in latent period 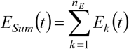
Total number in prodromal period 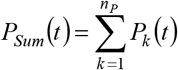
Total number in early infectious period 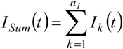
Total number in late infectious period 
Contact rate and force of infection
Contact rate 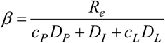
Force of infection 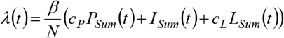
Stochastic treatment of the differential equations
The kind of epidemiologic events and the duration between two consecutive events are calculated using random numbers. The simulations start with a fully susceptible population in which one individual (index case) is infected. The infection stage of the index case is picked at random, taking into consideration the different lengths of the latent, prodromal, early and late infectious period. In each simulation, the sum of all the rates that change the current state of the system is calculated as

A uniformly distributed random number r1∈[0,ξ] is then chosen, and the time Δt = −ln(r1)/ξ after which the next event occurs is calculated. All transition rates are arranged in an arbitrary order, and cumulative rates are calculated by adding their individual rates. A new uniformly distributed random number r2 ∈[0,ξ] is chosen, and the first transition in the order whose cumulative rate is larger than r2 is performed. If, for example, the event is an infection, one individual is removed from the group of susceptible individuals and added to the group of latent individuals of stage 1. New rates are calculated after each step, and the procedure is repeated. A more detailed description of the transformation of differential equation models to stochastic models can be found in Gillespie (1976) [13].
Parameters
N Population size
λ Force of infection
Re Effective reproduction number
β Effective contact rate
DE Average duration of the latent period
nE Number of stages for the latent period
ε Stage transition rate for the latent period(ε = nE / DE)
DP Average duration of the prodromal period
nP Number of stages for the prodromal period
φ Stage transition rate for the prodromal period (φ=np/Dp)
cP Contagiousness in the prodromal period (relative to the contagiousness in the early infectious period)
DI Average duration of the early infectious period
nI Number of stages for the early infectious period
γ Stage transition rate for the early infectious period (γ= nI/DI)
DL Average duration of the late infectious period
nL Number of stages for the late infectious period
δ Stage transition rate for the late infectious period (δ = nL/DL)
cL Contagiousness in the late infectious period (relative to the contagiousness in the early infectious period)