Abstract
The value of serological testing to inform the public health response to the SARS-CoV-2 pandemic is debated. Using a transmission model, we examined how serology can be implemented to allow seropositive individuals to resume more normal levels of social interaction while offsetting the risks. We simulated the use of widespread serological testing with realistic assay characteristics, in which seropositive individuals partially restore their social contacts and act as immunological ‘shields’. If social distancing is relaxed by 50% at the same time that quarterly serological screening is initiated, approximately 120,000 deaths could be averted and a quarter of the US population could be released from social distancing in the first year of the epidemic, compared to a scenario without serological testing. This strategy has the potential to substantially flatten the COVID-19 epidemic curve while also allowing a substantial number of individuals to safely return to social and economic interactions.
One Sentence Summary Informing relaxation of social distancing with serological testing can reduce population risk while offsetting some of the severe social and economic costs of a sustained shutdown.
SARS-CoV-2 emerged in China in late 2019 leading to a pandemic of COVID-19, with over 4.1 million detected cases and over 285,000 deaths globally as of May 11, 2020 (1). In the United States (U.S.), 1.3 million cases and 85,000 deaths were reported by that date (1). Unprecedented social distancing measures have been enacted to reduce transmission and thereby blunt the epidemic peak (i.e. “flatten the curve”). In early March, U.S. states began to close schools, suspend public gatherings, and encourage employees to work from home if possible. On March 17, 2020, the U.S. government issued national social distancing guidelines, leading to wider implementation of such policies. By mid-April, 95% of the U.S. (2) and over 30% of the global population were under some form of shelter-in-place order (3). Federal social distancing guidelines expired on April 30, 2020; in late April and May, many state and local governments relaxed stay-at-home orders partially or completely to move towards ‘re-opening’ (4).
Relaxing these initially effective social distancing policies will result in increased contacts and community transmission (5). A return to ‘business as usual’ will likely lead to exponential growth in cases, exceeding the capacity of health services (6). With the goal of maintaining the reproductive number at or less than one, public health efforts could allow a gradual return to some activities (4). Some degree of social distancing, together with enhanced hygiene and wearing of face masks, is likely to be maintained with stricter distancing measures for individuals at higher risk (7). Alongside these measures, widespread serological testing programs may help inform these new social distancing strategies while keeping deaths and hospital admissions at sufficiently low levels.
Recent serosurveys of SARS-CoV-2 in the U.S. vary in their estimates of seroprevalence but collectively suggest that infections likely far outnumber documented cases (8-10). If detectable antibodies serve as a correlate of immunity, serological testing may be used to identify protected individuals (11). While our understanding of the immunological response to SARS-CoV-2 infection remains incomplete, the vast majority of individuals experience seroconversion after infection (12) and convalescent plasma from recovered COVID-19 cases appears to improve outcomes in critically ill patients (13–15). Together, these data suggest that recovered individuals have some protection against subsequent reinfection. Once identified, test-positive individuals could return to pre-pandemic levels of social interactions and act as ‘shields’ (16). In this strategy, individuals who test positive would preferentially replace susceptible individuals in physical interactions, such that more contacts are between susceptible and immune individuals rather than between susceptible and potentially infectious individuals.
Such strategies, however, rely on correctly identifying immune individuals. There are currently twelve serological assays for detection of SARS-CoV-2 antibodies that have been approved for emergency use by Food and Drug Administration (17) with many others currently in development and approved in other countries (18). The performance of these tests vary considerably (17, 19, 20). For the purpose of informing social distancing policies, specificity rather than sensitivity is of primary concern. An imperfectly specific test will result in false positives, leading to individuals being incorrectly classified as immune. If used as a basis to relax social distancing measures, there is concern that this error could heighten risk for individuals who test positive and lead to an increase in community transmission.
We modeled the transmission dynamics of SARS-CoV-2 using a deterministic, compartmental SEIR-like model calibrated to death data (https://github.com/nytimes/covid-19-data) and ICU admissions (https://covidtracking.com/api). (Figure 1, Figure S1, Table S1) Recovered, susceptible, latently infected, and asymptomatic at rates that are functions of testing frequency, sensitivity (for recovered individuals), and specificity (for non-immune individuals). (Figure 1A) We model contacts at home, work, school, and other locations among three age groups: children and young adults (<20 years), working adults (20-64 years), and elderly (65+ years).
Methods diagram overview A) Overall model diagram. Serological antibody testing is shown by dashed arrows. Red dashed arrows indicate false positives (i.e., someone is not immune, but is moved to the test positive group) and occur at a rate that is a function of 1-specificity. True positives occur at a rate that is a function of the sensitivity. *Symptomatic infections in the test-positive group have similar severity to symptomatic infections in the not tested/test negative group, but symptoms are not recognized as being caused by SARS-CoV-2 unless symptoms are severe enough to warrant hospitalization. B) Schematic of modeled interventions. General social distancing reduces work, school and other contacts beginning on March 25, 2020 and these contacts are gradually reintroduced beginning on May 9, 2020 with schools and daycares re-opening on September 1, 2020.
On March 17, 2020, the U.S. federal government released guidance recommending working from home, postponing unnecessary travel, and limiting gatherings to less than 10 people (21). Under these measures, we assume all contacts at school and daycare were eliminated and contacts outside of home, work, and school (‘other’) locations were reduced by 75% (22) while contacts at home remained unchanged. In accordance with state and local governments relaxing distancing policies, we assume social distancing measures for the general population are relaxed starting May 9. At this time, work and other contacts are scaled to a proportion of their value under general social distancing based on a scalar constant, c, such that c=1 is equivalent to the scenario in which social distancing measures as put into place on March 17 are maintained and c=0 is equivalent to a return to pre-pandemic contact levels. We assume that schools and daycares remain closed until September 1, 2020 and that test-negative/untested individuals continue to work from home. (Figure 1B)
Individuals who test positive return to work and increase other contacts to normal levels. To reflect the placement of test-positive individuals in high-contact roles, we assume that contacts at work and other (non-home, non-school) locations are preferentially with test-positive persons. When shielding is 5:1, this implies that the probability of interacting with a test-positive individual is 5 times what would be expected given the frequency of test-positives in the population (α=4), following the model of ‘fixed shielding’ (described in (16)).
We consider a high-performance test with a specificity of 99.8%, consistent with the recently approved Roche assay, and a sub-optimal test with 96% specificity (similar to the approved Cellex assay) (17). We set test specificity to 50% to represent a scenario in which antibodies are not a reliable correlate of immunity, (i.e., the test cannot distinguish between immune and non-immune individuals).
Without any intervention, our model predicts that 86% of the US population would be infected with SARS-CoV-2 by January 2021, resulting in 940,000 deaths. Social distancing has the potential to greatly reduce this burden, with indefinite social distancing reducing cumulative deaths by 88% and leading to a flattened epidemic curve. If social distancing measures are relaxed prematurely, incidence rebounds and the benefit of early distancing is lost by the end of the epidemic (Figure S2, Table S2).
Reductions in social distancing may be implemented simultaneously with serological testing to reduce deaths and healthcare system burden (Figure 2, Figure 3). If social distancing measures are relaxed such that adults only reduce their contacts by 40% compared with pre-pandemic levels (c=0.5, Table S3) and schools reopen in the fall, 556,000 deaths would be expected by January 2021 (Figure 2). However, if annual serological testing of the US population (1 million tests/day) is implemented alongside relaxation of social distancing, expected deaths fall to 437,000, saving 119,000 lives. If monthly testing is achieved (10 million tests/day), expected deaths fall to 235,000, saving 321,000 lives. With monthly testing, 29% of the U.S. population would test positive by the end of one year and be able to return to work and increase other social contacts to pre-pandemic levels (Figure 3); 26% if annual testing is used.
The top row shows cumulative deaths by January 15, 2021 assuming schools reopen on September 1, 2020 for No Shielding (α=0) (left) and 5:1 Shielding (right). Colored lines show the extent of relaxing social distancing measures, based on the value of c. Dotted lines show 5 results for a weak immunity scenario, solid lines show results for a suboptimal test (96% specificity), and dashed line shows results for a high-performance test (99.8% specificity). The bottom row shows the fraction of the US population released from social distancing after 1 year for No Shielding (left) and 5:1 Shielding (right). Line colors correspond to testing levels; blue is monthly testing (10 million tests/day) of the US population. Results shown assume a 50% 10 relaxation of current social distancing levels for work and other contacts for those untested or testing negative and assume a test sensitivity of 100%.
Critical care cases over time by testing level (colors) and relaxation of social distancing levels (panels). c is the factor by which non-home, non-school contacts are reduced from their initial values. All panels assume schools reopen on September 1, 2020. The U.S. critical capacity is shown by the solid black line (97,776 beds (24))
The magnitude of this benefit depends on both the degree of immunological shielding and test specificity. If α=0 (no shielding), 557,000 deaths would be expected with monthly testing of the U.S. population, similar to if testing were not implemented at all. Higher levels of shielding could reduce population risk further if a highly specific test is used, with monthly testing leading to 180,000 deaths after one year (Figure S3). Using a less specific test (such as (23)) could increase population risk. For example, if monthly testing with a suboptimal assay were implemented without immunological shielding and a 50% relaxation in social distancing, 85% of the US population would be released from social distancing but 587,000 deaths would be expected, 31,000 more than if no testing were implemented.
Using a highly specific test (99.8% specificity), the fraction of the test positive population who remain susceptible at the end of the epidemic remains small (Figure S4). Testing about half of the U.S. population once a year is roughly equivalent to a 10% increase in social distancing intensity. (Figure 4) If social distancing is relaxed to pre-pandemic levels, higher levels of testing can lead to an increase in deaths if infection prevalence remains low due to a higher rate of false positives (lower positive predictive value). (Figure 3)
Contour plot of A) cumulative deaths and B) number of people released from social distancing as a function of the degree of relaxation of social distancing (1-c) and testing rate, on the log scale. Both panels assume a test specificity of 0.998 and a shielding factor of 5:1 (α=4).
For all scenarios, sustaining moderate levels of social distancing for test-negative and untested individuals can reduce peak epidemic burden (Figure 3). An immediate return to pre-pandemic levels of work and ‘other’ contacts would result in a peak burden of 269,000 critical care patients in late June. In contrast, delaying school opening until September and lower levels of social distancing (c=0.75, equivalent to total contacts reduced by 17.9% for adults), peak burden would be 45,000-118,000 critical care patients, near or below the current critical care capacity in the U.S. (estimated at 97,776 beds (24)).
Reopening schools in early fall is unlikely to trigger a second wave of infections unless nationwide lockdown is maintained until the start of the academic year (c=1). A secondary peak is more likely during the summer, after social distancing measures are initially relaxed. Note that our model does not account for any seasonal variation in transmissibility, which may impact SARS-CoV-2 transmission (25, 26).
There is an urgent need to identify strategies to permit safely easing social distancing measures and returning to productive levels of economic and social activity. Our results suggest that serological testing can make a substantial contribution to these efforts. Maintaining moderate social distancing (i.e., at half the current level) together with widespread serological testing (at least yearly testing) could release 24% of the population from social distancing by January 15, 2021. Moreover, if moderate shielding is employed, a strategy with serological testing results in up to 321,000 fewer deaths than a strategy without testing. Moderate relaxation of social distancing and shielding alongside monthly testing results in a flattened curve that provides time to improve treatments and expand healthcare capacity, which could further reduce mortality rates (26). Thus, serological testing would allow a substantial fraction of the population to return to work and other activities with relative safety, compared to a universal rollback of social distancing policies (Figure S2, Table S2).
An aggressive testing approach (one million tests per day) may appear unprecedented but is feasible. Other countries including Germany have implemented widespread serological testing, including repeat testing of the same individuals on a regular (i.e. monthly) basis (27). Although this would require a significant and rapid scale-up of testing capacity in the U.S., this has already been achieved for diagnostic PCR testing: the U.S. expanded testing from fewer than 1,000 tests per day in early March to nearly 250,000 tests per day in mid-May. Moreover, recently developed serologic tests are quicker to perform than RT-PCR, with a potential throughput of 300 tests/hour/machine, compared with 94 RT-PCR tests performed every 3 hours (28, 29). One manufacturer of these tests projects tens of millions of tests will be available by the end of May with capacity ramping up thereafter (28). Including other assays with similar performance as part of an overall testing strategy further improves feasibility.
Even if testing can be scaled up, legal and ethical concerns remain. Requiring evidence of a positive test to return to work creates strong incentives for individuals to misrepresent their immune status or intentionally infect themselves. A mass testing program must consider how such policies might enforce existing social disparities and guard against inequities in test availability (30, 31). Relatedly, a history of a positive antibody test should not change the clinical care of individuals with respiratory symptoms suggestive of SARS-CoV-2 infection if a PCR diagnostic test would otherwise be indicated.
While others have raised concerns that using an imperfect test to relax social distancing could increase population risk, we show that available diagnostic tests can form the basis of a successful shielding strategy. If testing employs the most specific assays available, the false positive rate would remain low and deploying immune individuals such that they are responsible for more interactions than susceptible individuals will decrease risk. If shielding is not employed, this benefit disappears and testing can become a liability, which explains why our findings differ from others who have examined the potential impact of serologic testing programs (32). In our model, cumulative deaths are not substantially impacted by the false positive rate: deaths are similar under scenarios assuming a sub-optimally specific test (96% specificity) and a high-performance test (99.8% specificity) except at very high testing rates. Thus, false positives are unlikely to substantively impact population-level risk at levels of specificity reported by recently authorized serologic tests (17, 33).
Although false positives are more important than false negatives for transmission risk, sub-optimal sensitivity also has implications for a mass testing strategy. Several recently authorized tests report near-perfect sensitivity, but these estimates were made under ideal conditions which are unlikely to reflect the realities of a mass testing program (17). Testing too soon after exposure or using a less sensitive test would reduce the cost-effectiveness of testing by missing truly immune individuals. Complementing serologic testing with PCR-based viral diagnostic testing could substantially increase the pool of test-positive individuals able to return to work and other activities. Strategies that employ both tests should be the subject of future studies.
Our models assumed random allocation of serological testing. In practice, targeting testing to specific groups, such as healthcare workers, nursing home care providers, food service employees, or contacts of confirmed or suspected cases might increase efficiency by increasing the test positive rate (and consequently, cost-effectiveness (34)), allowing for similar numbers of individuals to be released from social distancing at lower testing levels. This strategy would also decrease the false positive rate, an important consideration if a less specific test is used(35). Many healthcare organizations have already begun to offer antibody testing to their employees (36). The use of serological testing and shielding within healthcare settings represents a potential application of a more targeted strategy.
Compared to maintaining current levels of lockdown, relaxing social distancing always results in higher COVID-19 incidence in our models. However, policymakers and society-at-large may consider these trade-offs acceptable, given the high social and economic costs of sustained social distancing. Importantly, this calculation may change over time: the benefits of a serological testing and shielding strategy may decline as incidence declines, as the positive predictive value of the test declines and the number of individuals that test positive plateaus. The success of this strategy also depends on the degree to which shielding can be implemented. We have assumed a moderate degree of shielding (16); the extent to which it is possible to implement this in different settings will vary.
There remains much to learn about immunity to SARS-CoV-2 and we have made three critical simplifying assumptions in our model. First, we assume that antibodies are immediately detectable after resolution of infection. In reality, this likely occurs between 11 to 14 days post infection (37), similar to SARS-CoV-1 (38). A small fraction of recent infections would be undetected, but this would have a minor effect on our results. Second, we assume that immunity lasts for at least a year. Given that the virus has only been circulating for a matter of months in humans, both the duration of antibody protection and the extent to which those antibodies protect against future infections is unknowable. However, most individuals who are infected seroconvert (12), and ongoing studies of SARS-CoV-2 show that antibodies persist for at least 7 weeks (37). Third, we assume that antibodies detected by serology are a correlate of protection. Antibody kinetics of SARS-CoV-1 and MERS suggest that protection will last for at least months and as long as several years (38).
A serological testing strategy is only one component of the public health response to COVID-19, alongside diagnostic testing, rigorous contact tracing, and isolation efforts. If implemented simultaneously, such measures would likely reduce the extent of shielding required to achieve the same benefit, in addition to further reducing overall transmission.
In summary, our results suggest a role for a serological testing program in the public health response to COVID-19. While maintaining a degree of social distancing, serology can be used to allow people with positive test results to return to work and other activities while mitigating the health impacts of COVID-19.
Data Availability
Transmission model code and incidence data used are available at the links provided
https://coronavirus.jhu.edu/map.html
https://github.com/lopmanlab/Serological_Shielding
Funding
BAL and ANMK were supported by the Vaccine Impact Modelling Consortium; BAL and KNN were supported by NIH/NICHD R01 HD097175; BAL, KNN, and ANMK were supported by NIH/NIGMS R01 GM124280; JSW was supported by Simons Foundation (Scope Award ID 329108); JSW and CZ were supported by the Army Research Office (W911NF1910384); JSW was supported by National Science Foundation (1806606 and 1829636).
Author contributions
The model was designed by ANM and KNN, extended from an earlier version by JSW and CYZ. All authors designed model simulations, ANM and KNN conducted the analysis and ANM, KNN, and BAL wrote the first draft of the manuscript. JSW and CYZ provided critical review of the code, results, and conclusions.
Competing interests
BAL reports grants and personal fees from Takeda Pharmaceuticals and personal fees from World Health Organization outside the submitted work.
Data and materials availability
Data used for model calibration are available from ‘https://github.com/nytimes/covid-19-data’ and ‘https://covidtracking.com/api’. Code is available at ‘https://github.com/lopmanlab/Serological_Shielding’
Supplemental Material
Materials and methods
Model structure
We modeled the transmission dynamics of SARS-CoV-2 using a deterministic, compartmental SEIR-like model. (Figure 1) We assume that after a latent period, infected individuals progress to either asymptomatic or symptomatic infection. A fraction of symptomatic cases are hospitalized, with a subset of those requiring critical care. Surviving cases, both asymptomatic and symptomatic, recover and are assumed to be immune to reinfection. All individuals who have not tested positive and are not currently experiencing symptoms of respiratory illness are eligible to be tested. All hospitalized cases are tested prior to discharge. Recovered individuals are moved to the test positive group at a rate that is a function of the test sensitivity. Susceptible, latently infected, and asymptomatic cases may falsely test positive and are moved to the test positive group at a rate that is a function of test specificity. False positives may become infected, but the inaccuracy of their test result is not recognized unless they develop symptoms that are sufficiently severe to warrant hospitalization and health providers correctly diagnose COVID-19, overriding the history of a positive antibody test. The ordinary differential equations corresponding to this model are included below. All models were run using R in the package ‘deSolve’ in R version 3.6.2. Code is available at https://github.com/lopmanlab/Serological_Shielding. There are three age groups represented in the model: children and young adults (<20 years), working adults (20-64 years), and elderly (65+ years). We modeled age-specific mixing based on POLYMOD data adapted to the population structure in the United States (39 ,40). Contacts in this survey were reported based on whether they occurred at home, school, work, or another location. We model an outbreak that begins with the first cases in the U.S., which were estimated to have occurred in mid-January (41, 42).
Social Distancing
To account for variations in timing, we assumed that national social distancing began on March 25th. Although adherence to these measures varied geographically and is generally difficult to measure, we made several assumptions about how these policies have changed location-specific contacts. First, we assume that under these measures, all contacts at school and daycare were eliminated and that contacts outside of home, work, and school (‘other’) locations were reduced by 75%. We assume that contacts at home remained unchanged. To address differences in work-based contacts by occupation type, we classified the working adult population into three subgroups based on occupation: those with occupations that enable them to work exclusively from home during social distancing, those continuing to work but reduced their contacts at work (e.g., customer-facing occupations such as retail), and those continuing to work with no change in their contact patterns (e.g., frontline healthcare workers). Both the percent reduction in ‘other’ contacts and percent contact reductions at work for essential workers who can reduce their contacts were calibrated to deaths and critical care cases observed in the US under social distancing.
Phased re-opening
Overall. We consider a phased approach to re-opening that begins to relax social distancing restrictions on May 1, 2020 and that these changes begin to affect contact patterns one week later on May 9, 2020. At this time, we assume that schools and daycares remain closed but that social distancing measures for the general population can be relaxed, by allowing work and other contacts to be increased. To represent this, we scale ‘work’ and ‘other’ contacts to a proportion of their value under general social distancing based on a scalar constant, c, such that c = 1 is equivalent to the scenario in which social distancing measures as put into place on March 17 are maintained and c = 0 is equivalent to a return to pre-pandemic contact levels for both ‘work’ and ‘other’ contacts for essential workers and pre-pandemic contact levels for ‘other’ contacts for all other groups. We assume that all children return to school and daycare on September 1, 2020.
Testing. We consider how complementing relaxation of social distancing with serological testing could be used to release test-positive individuals from social distancing to act as shields, reducing population risk. We assume that testing begins on May 1, 2020, and that test results begin to affect contact patterns one week later on May 9, 2020. Individuals that test positive can return to work (if they are not already working) and increase their non-home and non-school contacts to normal levels. To represent the deployment of immune persons in customer-facing and other high-contact occupations, we assume that contacts at work and other (non-home, non-school) locations are preferentially with immune persons by specifying that the probability of interacting with a test positive person is 5 times what would be expected given the frequency of test-positives in the population (α = 4), modeled using ‘fixed shielding’ as described previously in (16). We consider alternative a values in a sensitivity analysis. While our main model simulations focus on a test with analytical performance similar to the Roche test (sensitivity=100%, specificity=99.8%) (16), we also considered a test with 96% specificity to account for the fact that testing might not always be administered as designed and that other, less accurate tests might also be used,. We consider how relaxing social distancing recommendations combined with different levels of serological testing (with testing frequency ranging from none to monthly testing of the US population) impacts the proportion of the population released from social distancing, total deaths, and peak health system burden.
Model calibration
The initial strength of national social distancing, probability of transmission per infectious contact (q) and the initial number of infections by age group were calibrated to deaths and critical care cases observed in the U.S. between January 15th and April 23, 2020, as stay at home orders around the nation began to expire in multiple states April 24, 2020 (43). Our goal was to obtain model parameters that produced death estimates within an order of magnitude of those reported, with a secondary goal of approximating total currently occupied beds in intensive care units across the country. For death data, we used data from the New York Times https://github.com/nytimes/covid-19-data and for ICU admissions we used data from the COVID Tracking Project https://covidtracking.com/api. In mid-April, our model suggests that 92% of deaths were reported and 52% of ICU admissions were correctly reported as being attributable to COVID-19. A comparison of modeled deaths and ICU admissions and data for the first 100 days of the outbreak (January 15-April 23) is shown in Figure S1. Based on this calibration, we seed the model with 171 infections (60 in children, 71 in adults, and 40 in the elderly). The calibrated probability of infection per contact is 3.9%, yielding a basic reproduction number of 3.1, similar to other models of SARS-CoV-2 transmission (44). The reduction in other contacts was estimated to be 75% and reduction in workplace contacts for reduced contact workers was 90%. These social distancing parameters correspond to a 64.7% reduction in overall contacts for working-age adults, which is consistent with initial data from reductions in face to face contacts, which ranged from 50-85% (22).
Model Equations
The ordinary differential equations describing the model are shown below for group i. The positive test group is denoted with the ‘+’ sign.
m1(t) and m2(t) are defined as follows (t = 107 is when testing starts, on May 1, 2020):
The left panel shows cumulative deaths and the right panel shows current ICU admissions. Data is shown in dashed lines and the model is shown in solid.
The force of infection λ(t) for the ith group is a function of the number of social contacts for age group i with each subgroup j at time t (xi,j(t)), the probability of infection given contact (q), the number of infections in each group at time t (infecj(t)), and the population size of each group at time t(nj(t)). The overall equation for λi(t) is shown below:
i and j take values of ch (children age 0-19 years), ad (adults age 20-65 years who are not working or working from home), el (older adults 65+yearsofage), rc (adults at work in ‘reduced-contact’ occupations, where they have fewer contacts than pre-pandemic), fc (adults as work in full contact occupations, where they have the same number of contacts as pre-pandemic).
The number of infectious individuals by age group and test status is equal to the sum of documented (symptomatic) cases and a fraction of the undocumented (asymptomatic) cases, where this fraction asy corresponds to the relative infectiousness of undocumented cases. This is shown below for children:
Model parameters
Parameters used in the model simulations are shown in Table S2. We assume that the size of the working population is stable over the duration of the simulation. Although this may not be the case as unemployment increases throughout the pandemic, the rate at which unemployment has increased so far has been time-varying and its future trajectory is unknown.
Where possible, parameters were taken from prior literature. However, data from the initial stages of the outbreak were lacking for the probability of transmission per contact (q) and the initial strength of social distancing. These parameters were calibrated to initial outbreak dynamics. See section S9 for comparison of modelled and observed incidence. The basic reproduction number of this model is 3.1. See section S4 for matrix algebra used to estimate the basic reproduction number.
Parameters used in model simulations. Values shown in parentheses represent a range, used to perform sensitivity analysis.
Estimation
The dynamics of the system and 
are determined by how the outbreak would proceed at time zero in the absence of any interventions. Therefore, we assume no testing at time 0, no social distancing, and no differences in worker contact levels (i.e., all groups mix at the population-average level prior to the outbreak). In this situation, there are only 3 population subgroups at time zero:
The λi for each group is defined as follows.
The matrices 
and 
corresponding to these equations are:
To derive an expression for 
we inverted the 
matrix and multiplied by 
. The dominant eigenvalues of this matrix can be computed, but are very complex and are therefore not shown here. It is notable that because hospitalized cases do not contribute to the force of infection, the value of 
does not depend on γhs or γhc. Based on the calibrated model parameters, this yields a basic reproduction number of 3.1.
Naive social distancing interventions
If social distancing were completely relaxed prior to the end of the epidemic, our model predicts that transmission would quickly rebound. Predicted critical care epidemic curves are shown in Figure S2 and cumulative infections and deaths are shown in Table S2.
Critical care beds needed per day for different intervention scenarios assuming a 75% reduction in other contacts, school closures, nonessential workplace closures, and 90% reduction in workplace contacts for reduced contact employees for the duration of distancing
Cumulative infections and deaths after 1 year for social distancing scenarios without testing.
Contact matrices
Baseline contacts
Baseline contact matrices for ‘work’ contacts, ‘school’ contacts, ‘home’ contacts, and ‘other’ contacts were taken from (38). To expand these baseline matrices to the 5 population groups in our model (separating the adult population into fc, rc, and h classes), we multiplied all contacts with adults xi,ad by the proportion of the adult population falling into each class. We define the fraction of the population falling in each working group as follows:
For baseline contact matrix values based on (38)., we have:
For simplicity, we assume that baseline interactions between worker subgroups are only assortative with respect to age (and not with respect to occupation type). To expand this matrix to a 5×5 matrix we use the following notation, where rows 2, 3, and 4 correspond to the work from home, reduced contact, and full contact occupation groups, respectively:
Based on these proportions, we define xi,h, xi,rc, and xi,fc as follows:
Contacts under social distancing
After social distancing has begun, we assume that:
Home contacts remain the same.
Schools and daycares close.
Only working age adults continue to work. Baseline workplace contacts for children and young adults under 20 years of age are nearly zero (average 0.84 contacts/day) and the average workplace contacts for the elderly is 0, so this does not appreciably impact our results.
All workers who are able work from home.
Adults continuing to work reduce their workplace contacts by constant preduced.
Other contacts are reduced by scalar constant sd.other.
The values of p.reduced and sd.other were estimated by comparing projected incidence from our model with that observed in the U.S. under social distancing measures.
The revised contact matrix for work contacts then becomes:
The revised contact matrix for other contacts becomes:
Contacts during initial relaxing of social distancing
When phase 1 begins on May 1, 2020, we assume that:
Testing begins, moving test-positive individuals to the test positive group
Home contacts remain the same, but their distribution is driven by the proportion of test-positives in the general population.
Adults who were working from home may return to work if they test positive. Upon returning to work, their workplace contacts are assortative with respect to test status (but not with respect to occupation type).
Workers in reduced contact occupations increase their workplace contacts based on the intensity of social distancing maintained. Work contacts are preferentially with test-positive individuals, as determined by α.
Schools remain closed.
Other contacts are increased for test positive individuals to their pre-pandemic levels. Other contacts continue to be reduced for test negative/untested individuals based on the intensity of social distancing maintained. Other contacts are preferentially with test-positive individuals, as determined by α.
Because testing has begun, all contact matrices are dependent on the proportion of the population that has tested positive and been released from social distancing at time t. We define this proportion as ri(t), where (1 − ri(t)) is the fraction of the population who has not yet tested positive.
We assume that social distancing parameters are relaxed from their initial values as follows:
For contact matrices of work and ‘other’ contacts, we implement shielding factor α, which increases the probability of contacting a test-positive individual according to their prevalence in the population (achieved by multiplying expected contact rates due to prevalence by scaling factor α + 1). To account for the fact that, when prevalence is high, (α + 1)ri(t) may exceed 1, we introduce a variable si(t):
This shielding structure is similar to ‘fixed shielding’, previously described by Weitz et al [?] in that it preserves the baseline number of contacts and increases contacts for test positive individuals by 1 + α, as shown below:
The structure of all three matrices (home, work, and other) is given by CM:
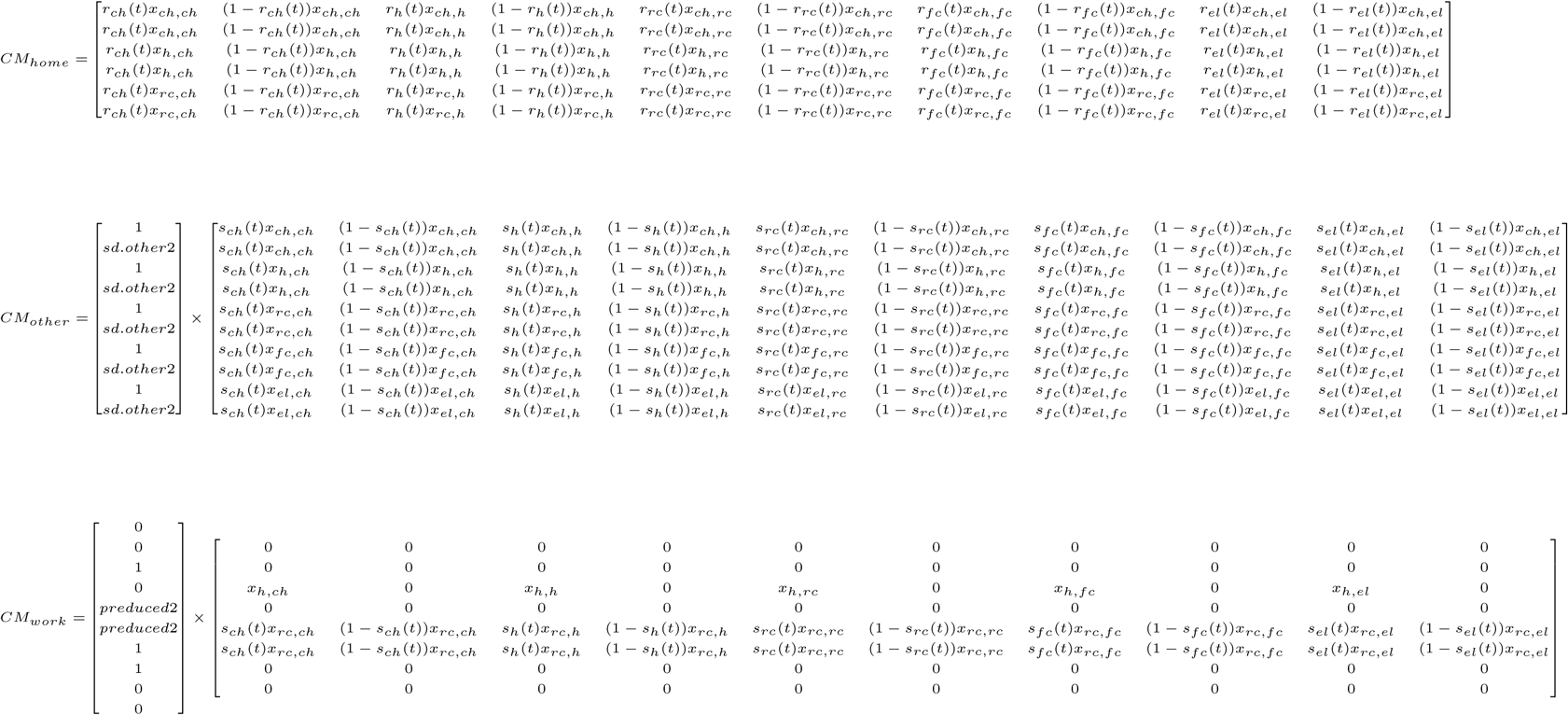
Contacts after schools reopen on September 1, 2020
When phase 2 begins, schools re-open and children return to school, setting the school contact matrix to its baseline values. Because some children will have tested positive, contact probabilities are proportional to the fraction of the population who has tested positive at each time point (same structure as the home matrix from phase 1). All other matrices remain the same.
Contact reductions by levels of c
Reduction in contacts corresponding to different values of c
Sensitivity analysis for higher levels of shielding (α = 9, 10:1 shielding)
We also considered higher levels of shielding to see how this change would impact cumulative deaths and the fraction of the population released from social distancing. While 10:1 shielding did result in fewer deaths at high testing levels, the total impact was minimal (Figure S3).
The left panel shows cumulative deaths by January 15, 2021 by social distancing relaxing strategy assuming schools reopen on September 1, 2020. Colored lines show levels of relaxing social distancing measures based on the value of c. The right panel shows the fraction of the US population released from social distancing after 1 year assuming a 50% relaxation of current social distancing levels or work and other contacts for those untested or testing negative and a 96% test specificity. Line colors correspond to testing levels, with blue being 10 million tests/day (monthly testing of the US population). Both panels are for 10:1 Shielding (α = 9).
Test performance over time
While not all test positive individuals are truly immune, the proportion of immune persons is always far greater in the test-positive population than the test-negative/untested population. Thus, even though the positive predictive value for a test does not approach 100% as the epidemic proceeds and a substantial number of truly susceptible individuals are identified as positive, preferential interaction with test-positive individuals tends to decrease risk. Higher testing rates tend to lead to lower immunity in the test positive population because a greater number of false positives are released from social distancing, and when shielding is strong these test positives mix to a greater extent with the test-negative/untested population, contributing to ongoing transmission. The level of immunity in the test positive population is shown in Figure S4 below for 5:1 shielding. Overall immunity is higher in the test-positive population (e.g., fewer false positives) when alpha is smaller (not shown).
Fraction of test positives who are still susceptible to COVID-19 over time based on the testing rate (panels) and the intensity of social distancing (line colors) for 5:1 shielding (α = 4). All panels assume a test with 99.8% specificity.
Acknowledgments
We thank Timothy Lash, Andreas Handel, Carly Adams, Julia Baker, Carol Liu and Avnika Amin for useful comments.
References and Notes
