Effect of emergency declaration for the COVID-19 outbreak in Tokyo, Japan in the first two weeks

Introduction

To control the COVID-19 outbreak in Japan, the Prime Minister Abe declared an emergency on April 7 and applied countermeasures starting from April 8 [1]. The declared measures required residents of seven prefectures, collectively accounting for 44.5% of Japan’s population, to restrict their trips outside the home voluntarily. Voluntary compliance means that the declared measures were not enforced as law. People were not arrested even if they do not comply with this government declaration. At the same time, the policy required the reduction of contact by 70–80%, based on the author’s earlier research [2]. However, the share of the population cooperating with government requirements without law enforcement has remained uncertain. Therefore, this policy’s effects must be evaluated as nearly and in as real-time a manner as possible. If the reproduction number after the emergency declaration (R_e) is less than one, then the government would be able to rescind the declaration earlier. If greater than one, and especially of greater than two, then a more powerful policy, including law enforcement, might be necessary. Therefore, we undertook preliminary evaluation of the effect as of April 14, at one week after the declaration was issued.

Method

The COVID-19 outbreak in Japan, which occurred from January 14, and its related countermeasures, are divisible into four periods. The national government required sports and entertainment events to be canceled in Japan for two weeks from February 26 through March 19 according to a government advisory. At the same time, it was advised that small business and private meetings be cancelled voluntarily. Moreover, from March 3, almost all schools were closed to control the spread of the infection until spring vacation began in the middle of March. The policy was designated as voluntary event cancellation and school closure(VECSC). Consequently, the COVID-19 outbreak can be divided into four distinct periods: before VCSEC through February 26, VCSEC through March 19, and after VCSEC through April 7, and the after emergency was declared. We defined the reproduction numbers for the respective periods as R₀, R_v, R_a, and R_e.

Onset dates were sometimes unreported. Therefore, we estimated the onset date. To do so, we inferred a distribution of the length from onset to reporting based on patients for whom onset dates were available. Then we applied this empirical distribution to patients for whom onset dates were not available. Letting f(k) represent this empirical distribution and letting Nt denote the number of patients for whom onset dates were not available published at date t, then the number of patients for whom the onset date was t-1. The number of patients for whom onset dates were not available was estimated as f(1)Nt. Similarly, the number of patients with onset date t-2 and whose onset dates were not available was estimated as f(2)Nt. Therefore, the total number of patients whose onset date were not available, given an onset date of s, was estimated as Σ_k=1f(k)Ns+k for a long time passed from s.

Moreover, the reporting delay for published data from MHLW might be considerable. In other words, if s+k was larger than that in the current period t, then s+k represents the future for period t: thus Ns+k was not observable. Such a reporting delay causes an under-estimation bias in the number of patients. Therefore, we must adjust it as Σ_k=1^t-sf(k)Ns+k /Σ_k=1^t-sf(k). Similarly, patients for whom the onset dates were available are expected to be affected by the reporting delay. Thus we have Ms|t /Σ_k=1^t-sf(k), where Ms|t represents the reported number of patients for whom onset dates were within period s extending until the current period t.

We applied a simple susceptible–infected–recovery (SIR) model [3,4] to the epidemic curve for Japan, with 120 million populations. We assume an incubation period calculated according to the empirical distribution.

Symptomatic and asymptomatic states continued for one week and then moved to a recovery state with probability of one. We are not concerned about outcomes or necessary medical resources in this model. Therefore, the state of death or hospitalization was not incorporated into the model. Asymptomatic cases cannot be observable unless complete laboratory-based surveillance is performed. One exceptional study found the asymptomatic cases to be 3/23 among elderly people [5]. For these analyses, the powers of infectivity among severe patients and mild patients were equal. Moreover, we assumed that asymptomatic cases have the same power of infectivity as symptomatic cases have [5]. The distribution of infectiousness in symptomatic and asymptomatic cases was assumed to be 30% on the onset day, 20% the following day, and 10% for the next five days [5].

We sought R₀, R_v, R_a, and R_e.to fit the data to minimize the sum of absolute values of discrepancies among the bootstrapped epidemic curve and the fitted values. The estimated distribution of three reproduction numbers was calculated using 10,000 iterations of bootstrapping from the empirical distribution of the data obtained for symptomatic patients.

We estimated the results sequentially as follows: We first estimated R₀ as the best fit to bootstrapped data in the pre-VECSC period. Then based on the obtained R₀ and course of the outbreak in the pre-VECSC period, we estimated R_v as the best fit to bootstrapped data for the VECSC period. Similarly, based on the obtained R₀ and R_v, we estimated R_a as the best fit to bootstrapped data in the post-VECSC period. Finally, based on the obtained R₀, R_v, and R _a, we estimated R_e as the best fit to a bootstrapped data after the emergency was declared. For each step, reproduction numbers were grid-searched in the interval of (0, 10) by 0.001 resolution.

Results

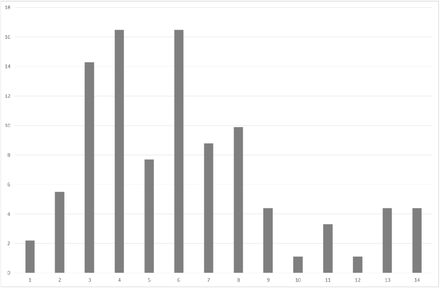
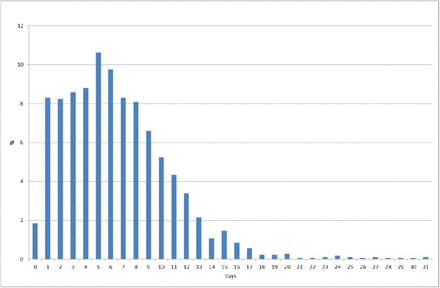
Figure 1 depicts the empirical distribution among incubation periods of 91 cases for which exposure dates and onset dates were reported by MHLW. Its mode was six days. Its average was 6.6 days. Figure 2 depicts the empirical distribution of duration from onset to report. We adjusted the reporting delay based on this distribution.

• Download figure
• Open in new tab

Figure 1:

Empirical distribution of incubation period published by Ministry of Labour, Health and Welfare, Japan

(%)

Notes: Bars indicates the number of patients by incubation period among 59 cases whose exposed date and onset date were published by Ministry of Labour, Health and Welfare, Japan.

• Download figure
• Open in new tab

Figure 2:

Empirical distribution of duration from onset to report by Ministry of Labour, Health and Welfare, Japan

(%)

Note: Bars indicates probability of duration from onset to report base on 657 patients whose onset date was available in Japan. Data source was Ministry of Labour, Health and Welfare, Japan.

The value of R₀ before VECSC was introduced was estimated as 1.267; its range was [1.214, 1.341]. However, R_v during the VECSC period when measures were introduced was estimated as 2.360 [1.844, 2.623]. After VECSC, R_a was estimated as 2.307 [2.035, 2.794]. After the emergency declaration, R_e decreased dramatically to be 0.462 [0.347, 0.514]. The null hypothesis that R_v and R_a were equal was not rejected, however, all other pairs were equal was rejected at 5% significant level.

Discussion

We applied a simple SIR model to all cases, including asymptomatic cases that had not been incorporated into the model to date. An earlier study [7–10] estimated R₀ for COVID-19 as 2.24–3.58 in Wuhan. Our R₀ obtained before VECSC was smaller than the previous studies, however, reproduction numbers in VECSC period and after VECSC were almost comparable. However, an earlier study [11] estimated R₀ in Japan as 0.6 as of the end of February, which was the period mainly before the VECSC was implemented. Such a low number might mislead policy efforts for countermeasures in Japan as it adheres to contact tracing efforts to detect clusters. Outbreaks contained themselves. Emergency declarations would be unnecessary if 0.6 is correct.

Our previous study estimated R_e in the first a week after the emergency declaration at nationwide was 0.083 [0.067, 0.105]. However, the present study in Tokyo in the two weeks after declaration was 0.758 [0.631, 0.879] Even it was lower than one, it increased to be ten time higher from a week in nationwide. It might suggest the effect of the emergency declaration has been gradually disappearing or in Tokyo, it was higher than in nationwide.

Moreover, reproduction number in the VECSC period and after VECSC were almost the same in Tokyo, though in nationwide, reproduction number in the VECSC period (1.028 [0.965, 1.191]) was much smaller than after VECSC (3.237 [3.005, 3.441]). This might means that VECSC was ineffective in Tokyo but effective other than Tokyo. In this sense, the effect of the emergency declaration might weak in Tokyo comparison with other area.

One must be reminded that these results reflect only those at two weeks after the emergency declaration. The reproduction number probably changed thereafter continuously. Therefore, we have to monitor it carefully in the next two weeks when emergency declared and after disappeared the declaration.

Conclusion

Results demonstrated that the reproduction number declined in the two weeks after the emergency declaration to be less than one, however, it might increase since the first week. The reproduction number must be monitored carefully and continuously. We hope that the present study contributes to government decision-making about cessation of the emergency declaration.

This study was based on the authors’ opinions. The analyses and results do not reflect any stance or policy of our affiliations.