Abstract
Objective To infer Covid-19 incubation time distribution from a large sample.
Method Based on individual case data published online by 21 cities of China, we investigated a total of 136 COVID-19 patients who traveled to Hubei from 21 cities of China between January 5 and January 31, 2020, remained there for 48 hours or less, and returned to these cities with onset of symptoms between January 10 and February 6, 2020. Among these patients, 110 were found to be aged 15 – 64, 22 aged 65 – 86, and 4 aged under 15.
Findings The differential incubation time histogram of the two age groups 15 – 64 and 65 – 86 are adequately fitted by the log normal model. For the 15 - 64 age group, the median incubation time of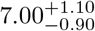 
days (uncertainties are 95 −0.90 % CL) is broadly consistent with previous literature. For the 65-86 age group, the median is 
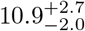days is statistically significantly longer. Moreover, for −2.0 this group, the 95 % confidence contour indicates the data cannot constrain the upper bound of the log normal parameters µ, σ by failing to close there; this is because the sample has a maximum incubation time of 17 days, beyond which we ran out of data even though the histogram has not yet peaked. Thus there is the potential of a much longer incubation time for the 65-86 age group than 10 – 14 days. Only a much larger sample can settle this.
1. Introduction
The incubation time of Covid-19 [1] and the closely related question of asymptomatic case numbers are two topics of major interest and concern. On the former, the research results presented here for the main age group of 15-64 broadly corroborates previous studies [2, 3, 4, 5, 6], but for the elderly group of 65-86 years the incubation time we report below is significantly longer.
For nearly every city in China, daily information on list of COVID-19 cases is released officially to the Chinese social media WeChat accounts of respective cities. However, only a minority of cities include in their official release clear information on the day of symptom onset, which is required in estimating incubation period. We extracted the information so released between January 22 and February 15, 2020 and compiled a list of patients with COVID-19 who have traveled to Hubei, the origin of the COVID-19 pandemic, from cities which reported the day of symptom onset. The supplementary Excel file containing these raw data on COVID-19 cases reported from 21 cities of China outside Hubei: patient case number, age, sex, first and last day in Hubei, and first day with symptoms.
In the current investigation we included only those COVID-19 patients who stayed in Hubei for at most two calendar days. The day of exposure was taken as the first day to Hubei if the patient stayed in Hubei for one calendar day; or as the middle of the first and second day in Hubei if the patient stayed for two calendar days. By excluding COVID-19 patients who stayed in Hubei for more than two days, one can better define the the day of exposure. The incubation period for each COVID-19 patient is inferred as the number of days between exposure and symptom onset.
2. Log normal distribution
As will be shown below, the distribution of incubation times may adequately be fitted with a log normal distribution for the two age groups mentioned above, suggesting that the incubation time τ (in days) is a multiplicative variate. Specific to the problem of Covid-19, it seems reasonable to envisage an inverse proportionality relationship between the virus growth rate 1+r and τ, and the sample average growth rate is
where N is the sample size (or number of measurements of the incubation time τ). Since τj ∝ 1/(1 + rj) this means
or, equivalently, both ln(1 + r) and ln τ are additive variates. Moreover, if ln(1 + rj) is normally distributed because 1 + rj itself is a geometrically many times averaged growth rate of the virus inside the human body (i.e. the Central Limit Theorem may apply to ln(1 + rj)), the distribution of τj would then be a log normal1 of (arithmetic) mean µ and standard deviation σ. Thus the expected number of cases within some incubation time interval k, or incubation time τk = kτ0, is
with the coefficient 1/τk originating from the relationship between logarithmic and linear intervals, viz. d ln τ = dτ/τ.
The applicability of the log normal model to the Covid-19 incubation times distribution compels one to calculate the mean incubation time as the geometric mean (2) at least as an alternative, as we shall do in the following section.
3. Fitting the data
The usual way of fitting a multi-parameter model to the data is by minimizing the χ2 statistic
w.r.t. the model parameters α, β, γ, …, where nk ≡ nk(α, β, γ, …) is the number of cases for incubation time interval k as expected by the model, 
is the observed number of cases, and 
is the expected model variance assuming Poisson fluctuation in the case counts. In the case of the currently scrutinized log normal model distribution consisting of three parameters α = µ, β = σ, and γ = n0 (where µ, σ, and n0 are as in (3)), 95 % confidence intervals δµ, δσ, and δn0 for the best-fit parameters may be inferred from the Δχ2 criterion discussed below. For a log normal quantile q = q(m) = eµ+mσ, Δχ2 also yields δq. Yet an alternative method is to take advantage of the independence of µ and σ in the model by writing
It turns out, however, that the fitting technique of (4) leads to large uncertainties in some parameters of interest, including those computed within the dynamic range of incubation times as set by the data. This is especially the case for the second of the two age groups, consisting of age 65-86 years patients, where the incubation time span of the model is significantly wider than the data. Below we present a slight variation of the method in (4) which avoids the problem.
To facilitate introducing the modified model fitting algorithm we first remind the reader of the standard maximum likelihood method2, which relies upon the nk ≫ 1 limit for all time intervals k, the limit where a Poisson distribution of counts tend to a Gaussian with equality between variance and mean. Thus the likelihood of a match between the number of counts nk predicted by the model and observational data 
for all incubation time intervals k is given by the conditional probability
and one’s task is to maximize P (data|model) w.r.t. the model parameters α, β, γ, …, where m is the total number of time intervals spanned by the data. If the number of counts per bin does not satisfy nk ≫ 1, however, the distribution of counts will not be normal, i.e. it will not be genuinely Poisson, in which case the expression on the right side of (6) is not strictly valid. In this limit, which does apply to the second of our two age groups (viz. 65 – 86 of age), one should use likelihood ratios [7] instead of (6), but because the difference between the two output parameter values are small compared to their uncertainties there is no real advantage in deviating from (6); we simply feel that for completeness sake this subtle point should be mentioned.
The maximization of (6) w.r.t. model parameters is obviously the same as minimizing χ2 as given in (4). Explicitly, if one writes, in the context of the log normal model (3),
the procedure would be equivalent to solving
Thus there are 3 equations in 3 unknowns, and the minimization process is fully deterministic.
If, as mentioned above, the total incubation time mτ0 spanned by the entire database is not long enough to clinch the full extent of the log normal distribution, one will have to constrain the fitting procedure to ensure that the area under the log normal is exactly equal to the total number of cases N over the time mτ0. The specific question one seeks to answer here is: given there are N cases to be randomly distributed into m time intervals in accordance with a prescribed set of average proportions {nk}, k = 1, 2, …, m satisfying
and nk = nk(n0, µ, σ), how would one tune n0, µ, and σ to maximize the likelihood of the hypothetical distribution agreeing with the data, when Poisson counting uncertainties in the latter are taken into account? Note that the model for nk does not have to cut off at k = m, i.e. (9) is merely there to enforce the equality between expected and actual total number of cases within the full range of incubation times available to the study. In this way, one is obliged to respect only those ‘in range’ parameter values ensuing from the best fit model.
Thus one would now extremize the statistic
by requiring
where the vanishing of the last partial derivative enforces the area (λ is a Lagrange multiplier). Once again there are 4 equations solving for 4 unknowns, and the number of free parameters is reduced from the previously 3 to currently 2 (note however that the area constraint is not as simple as fixing n0; note also that the degrees of freedom of the whole problem is increased from the m – 3 to m − 2).
Turning to the confidence interval for an interested parameter η(nk) = η(µ, σ, n0), such as the expected (arithmetic) mean incubation time within the observation interval mτ0,
one could re-extremize F subject to yet another additional constraint which ensures η equals some fixed value η0 by invoking one more Lagrange multiplier ν to form the G statistic,
and requiring
The resulting increase in χ2 w.r.t. (11), Δχ2, is also χ2 distributed with one degree of freedom, because the extra constraint enforced by ν has likewise increased the degrees of freedom by one3. Thus, to obtain the 95 % confidence interval in η, one needs to find the value of η0 such that (14) leads to a χ2 increase of Δχ2 = 3.8. This procedure applies if η is a mean, variance, or quantile, or any other attribute of the distribution.
By adopting the aforementioned procedure, we obtained the best-fit parameters as shown in Table 1, the goodness of fit in Figures 1 and 2, cumulative frequencies in Figures 3 and 4, and 95 % confidence contours in Figure 5, for the two age groups 15-64 and > 65.
Parameters of the best log normal fit to the two age groups. µ and σ are as defined in (3); while the other parameters are calculated by applying the best-fit model to the incubation time range of 17 days, which is the full range spanned by the data (true for both age groups). The information on each parameter comprises an expectation value sandwiched between the lower and upper uncertainty limit, both of which are 95 % confidence (note that for the 65+ age group their upper µ and σ uncertainties are not constrained by the data, because the data have not revealed the other side of the peak of the differential probability distribution, see Figures 2 and 5).
Best fit log normal distribution of the 15-64 age group is plotted against the data. Vertical error bars are the Poisson 
uncertainties in the counts, while horizonal bars mark the duration of 1 day for each time bin. The goodness-of-fit is given by χ2 = 9.44 for 15 d.o.f., or a 85.3 % probability of rejecting the null hypothesis (namely the hypothesis that the match between data and model occurred purely by random chance).
Best fit log normal distribution of the 65-86 age group is plotted against the data. Vertical error bars are the Poisson 
uncertainties in the counts, while horizonal bars mark the duration of 1 day for each time bin. The goodness-of-fit is given by χ2 = 7.85 for 15 degrees of freedom, or a 93.0 % probability of null hypothesis rejection (for comparison the Gumbel (log Weibull) model scored, under the same fitting criteria, χ2 = 8.17, or 91.7 % probability of null hypothesis rejection). Note however that for this age group the data have not revealed the other side of the peak of the differential probability distribution.
Cumulative frequency distribution for the 15-64 age group. Solid line is the best-fit log normal model for the differential distribution, while dotted lines mark the 95 % confidence (or Δχ2 = 3.8 for one degree of freedom, see text) uncertainties of the model. Vertical error bars for the data are Poisson counting fluctuations (1-σ, and correlated among the time bins because of the accumulation of counts), while horizonal bars mark the duration of 1 day for each time bin.
Cumulative frequency distribution for the 15-64 age group. For more information see the caption of the previous graph.
95 % (i.e. χ2 + 3.8) confidence contours identifying the likelihood of pairs of µ and σ values. The central black dot locates the best fit model. Note the upper limits of both model parameters are unconstrained by the data in the case of the 65-86 age group.
4. Conclusion
The two age groups being analyzed are clearly distinct samples. For the 15 - 64 age group, the median incubation time of 
days (uncertainties are 95 % CL, see Table 1) is broadly consistent with previous measurements [2, 3, 4, 5, 6]. For the 65-90 age group, the median is 
days is statistically significantly longer. The other equally importantly point is, as revealed by the open confidence contour in Figure 5b, the inability of the 65-86 age group data in constraining the upper bound of the model parameters µ, σ. This is because the sample of N = 22 cases here has a maximum incubation time of 17 days, beyond which one ran out of data even though the differential case histogram has not yet peaked (Figure 3). This indicates the potential of much longer Covid-19 incubation time for age 65-86 years old patients. It should also be pointed out that we attempted another model, viz. the Gumbel (or log Weibull) distribution, to see if the situation improves, but the goodness-of-fit turns out to be worse than the log normal (see the caption of Figure 3 for details). Indeed, only a larger sample for this age group can settle the question of the true median incubation time by clinching the tail of the distribution, equivalently by closing the 95 % CL contour of Figure 5b.
Footnotes
↵1 Under this assumption one can also derive (3) without enlisting the Central Limit Theorem, by consideration the viral interaction with the human body as a thermodynamic process with a fixed mean and variance, i.e. one which maximizes the Entropy − ∑j pj ln pj subject to the constraints pj = 1, ∑j pj ln τj = µ, and ∑j pj (ln τj)2 = σ2 + µ2.
↵2 The maximum likelihood method only works when there is independence of measurement intervals. Thus it is incorrect to apply the model to fitting the data of a cumulative (or integral) distribution, in which the counts of previous intervals affect the later ones.
↵3 To elaborate, the degrees of freedom equals the number of independent data points minus the number of free parameters in the model. If the last of the three quantities is reduced by one because of the incorporation of the ν-related constraint, the first will be increased by one.
