Abstract
Italy currently constitutes the epicenter of the novel coronavirus disease (COVID-19) pandemic, having surpassed China’s death toll. The disease is sweeping through Lombardy, which remains in lockdown since the 8th of March. As of the same day, the isolation measures taken in Lombardy have been extended to the entire country. Here, we provide estimates for: (a) the DAY-ZERO of the outbreak in Lombardy, Italy; (b) the actual number of exposed/infected cases in the total population; (c) the basic reproduction number (R0); (d) the “effective” per-day disease transmission; and, importantly, (e) a forecast for the fade out of the outbreak, on the basis of the COVID-19 Community Mobility Reports released by Google on March 29.
Methods To deal with the uncertainty in the number of actual exposed/ infected cases in the total population, we address a compartmental Susceptible/ Exposed/ Infectious/ Recovered/ Dead (SEIRD) model with two compartments of infectious persons: one modelling the total cases in the population and another modelling the confirmed cases. The parameters of the model corresponding to the recovery period, the time from the onset of symptoms to death, the case fatality ratio, and the time from exposure to the time that an individual starts to be infectious, have been set as reported from clinical studies on COVID-For the estimation of the DAY-ZERO of the outbreak in Lombardy, as well as of the “effective” per-day transmission rate for which no clinical data are available, we have used the SEIRD simulator to fit the numbers of new daily cases from February 21 to the 8th of March, the lockdown day of Lombardy and of all Italy. This was accomplished by solving a mixed-integer optimization problem with the aid of genetic algorithms. Based on the computed values, we also provide an estimation of the basic reproduction number R0. Furthermore, based on an estimation for the reduction in the “effective” transmission rate of the disease as of March 8 that reflects the suspension of almost all activities in Italy, we ran the simulator to forecast the fade out of the epidemic. For this purpose, we considered the reduction in mobility in Lombardy as released on March 29 by Google COVID-19 Community Mobility Reports, the effect of social distancing, and the draconian measures taken by the government on March 20 and March 21, 2020.
Results Based on the proposed methodological procedure, we estimated that the DAY-ZERO was most likely between January 5 and January 23 with the most probable date the 15th of January 2020. The actual cumulative number of exposed cases in the total population in Lombardy on March 8 was of the order of 15 times the confirmed cumulative number of infected cases. The “effective” per-day disease transmission rate for the period until March 8 was found to be 0.686 (95% CI:0.660, 0.713), while the basic reproduction number R0 was found to be 4.51 (95% CI: 4.14, 4.90).
Importantly, simulations show that the COVID-19 pandemic in Lombardy is expected to fade out by the end of May -early June, 2020, if the draconian, as of March 20 and March 21, measures are maintained.
Introduction
The butterfly effect in chaos theory underscores the sensitive dependence on initial conditions, highlighting the importance of even a small change in the state of a nonlinear system. The emergence of a novel coronavirus, SARS-CoV-2, that caused a viral pneumonia outbreak in Wuhan, Hubei province, China in early December 2019 has evolved into the COVID-19 acute respiratory disease pandemic due to its alarming levels of spread and severity, with a total of 1,579,690 confirmed infected cases, 346,780 recovered and 94,567 deaths in 184 countries as of April 3, 2020 ([1, 2]). The seemingly far from the epicenter, old continent became the second-most impacted region after Asia Pacific to date, mostly as a result of a dramatic divergence of the epidemic trajectory in Italy first, where there have been 143,626 total confirmed infected cases, 28,470 recovered and 18,279 deaths, and recently in Spain where there have been 152,446 total confirmed infected cases, 52,165 recovered and 15,238 deaths as of April 9, 2020 ([1, 2]).
The second largest outbreak outside of mainland China officially started on January 31, 2020, after two Chinese visitors staying at a central hotel in Rome tested positive for SARS-CoV-2; the couple remained in isolation and was declared recovered on February 26 [3]. A 38-year-old man repatriated back to Italy from Wuhan who was admitted to the hospital in Codogno, Lombardy on February 21 was the first secondary infection case (“patient 1”). “Patient 0” was never identified by tracing the first Italian citizen’s movements and contacts. In less than a week, the explosive increase in the number of cases in several bordering regions and autonomous provinces of northern Italy placed enormous strain on the decentralized health system. Following a dramatic spike in deaths from COVID-19, Italy transformed into a “red zone”, and the movement restrictions were expanded to the entire country on the 8th of March. All public gatherings were cancelled and school and university closures were extended through at least the next month.
In an attempt to assess the dynamics of the outbreak for forecasting purposes, as well as to estimate epidemiological parameters that cannot be computed directly based on clinical data, such as the transmission rate of the disease and the basic reproduction number, R0, defined as the expected number of exposed cases generated by one infected case in a population where all individuals are susceptible, many mathematical modelling studies have already appeared since the first confirmed COVID-19 case. The first models mainly focused on the estimation of the basic reproduction number R0 using dynamic mechanistic mathematical models ([4, 5, 6, 7]), but also simple exponential growth models (see e.g. [8, 9]). Compartmental epidemiological models like SIR, SIRD, SEIR and SEIRD have been proposed to estimate other important epidemiological parameters, such as the transmission rate and for forecasting purposes (see e.g. [7, 10]). Other studies have used metapopulation models, which include data of human mobility between cities and/or regions to forecast the evolution of the outbreak in other regions/countries far from the original epicenter in China [4, 11, 12, 6], including the modelling of the influence of travel restrictions and other control measures in reducing the spread ([13].
Among the perplexing problems that mathematical models face when they are used to estimate epidemiological parameters and to forecast the evolution of the outbreak, two stand out: (a) the uncertainty that characterizes the actual number of infected cases in the total population, which is mainly due to the large percentage of asymptomatic or mildly symptomatic cases experiencing the disease like the common cold or the flu (see e.g. [14]), and (b) the uncertainty regarding the DAY-ZERO of the outbreak, the knowledge of which is crucial to assess the stage and dynamics of the epidemic, especially during the first growth period.
To cope with the above problems, we herein propose a SEIRD with two compartments, one modelling the total infected cases in the population and another modelling the confirmed cases. The proposed modelling approach is applied to Lombardy, the epicenter of the outbreak in Italy, to estimate the scale of under-reporting of the number of actual cases in the total population, the DAY-ZERO of the outbreak and for forecasting purposes. The above tasks were accomplished by the numerical solution of a mixed-integer optimization problem using the publicly available data of daily new cases for the period February 21-March 8, the day of lockdown of all of Italy and the COVID-19 Community Mobility Reports released by Google on March 29.
Methodology
The modelling approach
We address a compartmental SEIRD model that includes two categories of infected cases, namely the confirmed/reported and the unreported (unknown) cases in the total population. Based on observations and studies, our modelling hypothesis is that the confirmed cases of infected are only a (small) subset of the actual number of infected cases in the total population [6, 14, 7]. Regarding the confirmed cases of infected as of February 11, a study conducted by the Chinese CDC which was based on a total of 72,314 cases in China, about 80.9% of the cases were mild and could recover at home, 13.8% severe and 4.7% critical [15].
On the basis of the above findings, in our modelling approach, the unreported cases were considered either asymptomatic or mildly symptomatic cases that recover from the disease relatively soon and without medical care, while the confirmed cases include all the above types, but on average their recovery lasts longer than the non-confirmed, they may also be hospitalized and die from the disease.
Based on the above, let us consider a well-mixed population of size N. The state of the system at time t, is described by (see also Figure 1 for a schematic) S(t) representing the number of susceptible persons, E(t) the number of exposed, I(t) the number of unreported infected persons in the total population who are asymptomatic or experience mild symptoms and recover relatively soon without any other complications, Ic(t) the number of confirmed infected cases who may develop more severe symptoms and a part of them dies, R(t) the number of recovered persons in the total population, Rc(t) the number of confirmed recovered cases and D(t) the number of deaths. For our analysis, and for such a short period, we assume that the total number of the population remains constant. Based on demographic data, the total population of Lombardy is N = 10m; its surface area is 23,863.09 kmq and the population density is ∼422 (Inhabitants/Kmq).
The rate at which a susceptible (S) becomes exposed (E) to the virus is proportional to the density of infectious persons I in the total population, excluding the number of dead persons D.The proportionality constant is the “effective” disease transmission rate, say 
, where 
is the average number of contacts per day and p is the probability of infection upon a contact between a susceptible and an infected. Our main assumption here is that only a fraction, say E of the actual number of exposed cases I(t) are confirmed through testing and reported as Ic(t). Thus, upon confirmation, we assume that the infected persons Ic go into quarantine, and, thus, they don’t transmit further the disease. A fraction of the confirmed Ic cases that is given by the fatality ratio 
dies with a mortality rate γ the inverse of which is the average time from the onset of symptoms to death, while the rest part of the Ic persons (1 − f) recover with a rate δc the inverse of which corresponds to the average time from the onset symptoms until the full recovery.
Thus, our discrete mean field compartmental SEIRD model reads:
The above system is defined in discrete time points t = 1, 2, …, with the corresponding initial condition at the very start of the outbreak (DAY-ZERO): S(0) = N − 1, I(0) = 1, E(0) = 0 Ic(0) = 0, R(0) = 0, Rc(0) = 0, D(0) = 0.
The parameters of the model are:
β(d−1) is the “effective” transmission rate of the disease,
σ(d−1) is the average per-day “effective” rate at which an exposed person becomes infective,
δ(d−1) is the average per-day “effective” recovery rate within the group of unreported (asymptomatic/mild) cases in the total population,
δc(d−1) is the average per-day “effective” recovery rate within the subset of confirmed infected cases that finally recover,
γ(d−1) is the average per-day “effective” mortality rate within the subset of confirmed infected cases that finally die, f is the probability that a confirmed case will die. This, is given by the “emergent” case fatality ratio defined as the ratio of confirmed deaths and the cumulative number of confirmed infected cases,
ϵ(d−1) is the fraction of the actual (all) cases of exposed in the total population that get confirmed. This proportionality rate quantifies the uncertainty in the actual number of unreported cases in the total popula-tion.
Here, we should note the following: as new cases of recovered and dead at each time t appear with a time delay (which is generally unknown but an estimate can be obtained by clinical studies) with respect to the corresponding infected cases, the above per-day rates are not the actual ones; thus, they are denoted as “effective/apparent” rates.
The values of the epidemiological parameters σ, δ, δc, γ that were fixed in the proposed model were chosen based on clinical studies.
In particular, in many studies that use SEIRD models, the parameter σ is set equal to the inverse of the mean incubation period (time from exposure to the development of symptoms) of a virus. However, the incubation period does not generally coincide with the time from exposure to the time that someone starts to be infectious. Regarding COVID-19, it has been suggested that an exposed person can be infectious well before the development of symptoms [16]. With respect to the incubation period for SARS-CoV-2, a study in China [17] suggests that it may range from 2–14 days, with a median of 5.2 days. Another study in China, using data from 1,099 patients with laboratory-confirmed 2019-nCoV ARD from 552 hospitals in 31 provinces/provincial municipalities suggested that the median incubation period is 4 days (interquartile range, 2 to 7). In our model, as explained above, 
represents the period from exposure to the onset of the contagious period. Thus, based on the above clinical studies, for our simulations, we have set 
.
Regarding the recovery period, in a study that is based on 55,924 laboratory-confirmed cases, the WHO-China Joint Mission has reported a median time of 2 weeks from onset to clinical recovery for mild cases, and 3-6 weeks for severe or critical cases [18]. Based on the above, and on the fact that within the subset of confirmed cases the mild cases are the 81% [15], we have set the recovery period for the confirmed cases’ compartment to be δc = 1/21 in order to balance the recovery period with the corresponding characterization of the cases (mild, severe/critical). The average recovery period of the unreported/non-confirmed part of the infected population, which in our assumptions experiences the disease like the flu or a common cold, is set equal to one week [19], i.e. we have set δ = 1/7. This choice is based on reports on the serial interval of COVID-19. The serial interval of COVID-19 is defined as the time duration between a primary case-patient (infector) having symptoms and a secondary case-patient having again symptoms. In our model, the period refers to the period from exposure to the onset of the contagiousness. In this period, obviously there are no symptoms. Thus, the serial interval in our model is 7 days (this is the average number of days in which an infectious becomes recovered and no longer transmits the disease). Importantly, there are studies (see e.g. Nushiura et al. [20]) suggesting that a substantial proportion of secondary transmission may occur prior to illness onset. Thus, the 7 days period that we have taken as the average period that an infectious person can transmit the disease before he/she recovers, reflects exactly this period; it refers to the serial interval for the cases that are asymptomatic and for cases with mild symptoms.
Finally, the median time from the onset of symptoms until death for Italy has been reported to be eight days [21], thus in our model we have set γ = 1/8. The case fatality rate until March 19 was ∼11%. Thus, for our computations we have set the CFR = 11% until March 19, and for forecasting we have set CFR to its current value on April 4, CFR = 17%.
On the other hand, the transmission rate β cannot be obtained by clinical studies, but only by mathematical models.
Regarding DAY-ZERO in Lombardy, what has been officially reported is just the date on which the first infected person was confirmed to be positive for SARS-CoV-2. That day was February 21, 2020, which is the starting date of public data release of confirmed cases.
Estimation of the DAY-ZERO of the outbreak, the scale of data uncertainty and the disease transmission
The DAY-ZERO of the outbreak, the per-day “effective” transmission rate β, and the level of under-reporting ϵ, were computed by the numerical solution of a mixed-integer optimization problem with the aid of genetic algorithms to fit the reported data of daily new cases (see the discussion in [22]) from February 21 to March 8, the day of the lockdown of Lombardy.
Here, for our computations, we have used the genetic algorithm “ga” provided by the Global Optimization Toolbox of Matlab [5] to minimize the following objective function:
where,
ΔXSEIRD(t), (X = I, R, D) are the new cases resulting from the SEIRD simulator at time t.
The weights w1, w2, w3 correspond to scalars serving in the general case as weights to the relevant functions for balances the different scales between the number of infected, recovered cases and deaths.
At this point we should note that the above optimization problem may in principle have more than one nearby optimal solutions, which may be attributed to the fact that the tuning of both DAY-ZERO and the transmission rate may in essence result in nearby values of the objective function. In order to quantify the above uncertainty in the optimization procedure, we created a grid of initial guesses within the intervals in which the optimal estimates were sought: for the DAY-ZERO (t0) we used a step of 2 day within the interval 27 December 2019 until the 5th of February 2020 i.e. ±20 days around the 16th of January, for β we used a step of 0.05 within the interval (0.3, 0.9) and for E we used a step of 0.02 within the interval (0.01, 0.29). The numerical optimization procedure was repeated 48 times for each combination of initial guesses. For our computations, we kept the best fitting outcome for each combination of initial guesses. Next we fitted the resulting cumulative probability distributions of the optimal values using several functions including the Normal, Log-normal, Weibull, Beta, Gamma, Burr, Exponential and Birnbaum-Saunders distributions and kept the one resulting in the maximum Log-likelihood (see in the Supporting Information for more details). For the computed parameters of the corresponding best distributions, we also provide the corresponding 95% confidence intervals. Note, that the expected values of the resulting distributions do not correspond to optimal values, due to the approximation that is introduced by the fitting procedure; however they correspond to expected/ most probable values around which an optimal solution is sought. Thus, for that purpose, we have used as initial guesses the mean values of the resulting distributions to the Levenberg-Marquard (implemented by the “lsqnonlin” function of matlab [23]) to find the optimal solution around this “representative point” as well the corresponding 95% confidence intervals. The step size for the finite differences computations was chosen based on the resulting minimum residual.
For our computations, we used the parallel computing toolbox of Matlab 2020a [23] utilizing 6 INTEL XEON CPU X5650 cores at 2.66GHz.
Estimation of the basic reproduction number R0 from the SEIRD model
Initially, when the spread of the epidemic starts, all the population is considered to be susceptible, i.e. S ≈ N. On the basis of this assumption, we computed the basic reproduction number based on the estimates of the epidemiological parameters computed using the data from the 21st of February to the 8th of March with the aid of the SEIRD model given by Eq.(1)-(7) as follows.
Note that there are three infected compartments, namely E, I, Ic and two of them (E,I) that determine the outbreak. Thus, considering the corresponding equations given by Eq.(2),(3),(4), and that at the very first days of the epidemic S ≈ N and D ≈ 0, the Jacobian of the system as evaluated at the disease-free state reads:
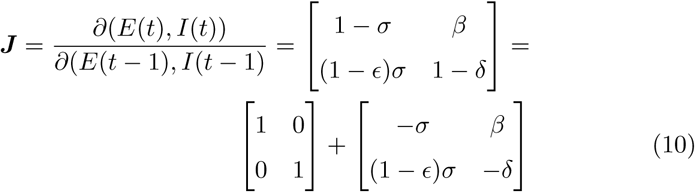The eigenvalues (that is the roots of the characteristic polynomial of the Jacobian matrix) dictate if the disease-free equilibrium is stable or not, that is if an emerging infectious disease can spread in the population. In particular, the disease-free state is stable, meaning that an infectious disease will not result in an outbreak, if and only if all the norms of the eigenvalues of the Jacobian J of the discrete time system are bounded by one. Jury’s stability criterion [24] (the analogue of Routh-Hurwitz criterion for discrete-time systems) can be used to determine the stability of the linearized discrete time system by analysis of the coefficients of its characteristic polynomial. The characteristic polynomial of the Jacobian matrix reads:
Where
The necessary conditions for stability read:
The sufficient conditions for stability are given by the following two inequalities:
The first inequality (13) results in the necessary condition
It can be shown that the second necessary condition (14) and the sufficient condition (15) are always satisfied for the range of values of the epidemiological parameters considered here.
Thus, the necessary condition (17) is also a sufficient condition for stability. Hence, the disease-free state is stable, if and only if, condition (17) is satisfied.
Note that in this necessary and sufficient condition (17), the fraction 
is the average infection time of the compartment I. Thus, the above expression reflects the basic reproduction number R0 which is qualitatively defined by 
Hence, our model results in the following expression for the basic reproduction number:
Note that for ϵ = 0, the above expression simplifies to R0 for the simple SIR model.
Model Validation and Forecasting
To validate the model, we used it to forecast the confirmed reported cases from March 9 to March 19, 2020, and then to forecast the fade-out of the outbreak in Lombardy.
Our estimation regarding the as of March 8 reduction of the “effective” transmission rate was based on the combined effects of prevention efforts and behavioral changes. In particular, our estimation was based both on (a) the COVID-19 Community Mobility Reports released by Google on March 29 [25], and (b) an assessment of the synergistic effects of such control measures as the implementation of preventive containment in workplaces, stringent “social distancing”, and the ban on social gatherings, as well as the public awareness campaign prompting people to adopt cautious behaviors to reduce the risk of disease transmission (see also [26, 27, 28, 29]).
On the basis of the Google COVID-19 Community Mobility Report released on March 29 [25], the reduction in the mobility in Lombardy during the period February 16-March 8, it had been reduced gradually by 40% in retail & recreation activities, and transit Stations, and by 20% in workplaces, while it had not been reduced in groceries, pharmacies and Parks. From March 8 to March 20 there was a gradual reduction reaching the 80% for all activities with respect to the baseline (February 16). Since March 20-21, when stricter measures have been taken, the reduction of the all the activities remains at 80% [25].
A further reduction may be attributed to behavioral changes. For example, it has been shown that social distancing and cautiousness reduce the disease transmission rate by about 20% [28]. On March 20, the government announced the implementation of even stricter measures that include the closing of all parks, walking only around the residency and not even in pairs, and the prohibition of mobility to second houses [30]. Extra measures were announced on March 21, including the closure of all public and private offices, and the prohibition of any pedestrian activity, even individually [31].
Thus, based on the above, it is reasonable to consider a 1-(1-0.5)(1-0.2) (an average of 50% contribution of the reduction of the mobility plus a 20% for the effect of social distancing) reduction in the effective transmission rate for the period March 8-March 19. In fact, on March 17, based on the release of mobile phone data, the vice-president of Lombardy, announced that the average mobility in the region (for distances more than 500 meters) had been reduced by a 50-60% with respect to the period before the lockdown [32]. For the period March 20-21, based on the Google data [25], we considered a reduction of 1- (1-0.8)(1-0.2) reflecting the draconian measures taken back then. Based on the above, we attempted a forecasting of the fade out of the outbreak.
Results
As discussed, for our computations we ran 48 times the numerical optimization procedure for each combination of initial guesses based on the daily reported new cases from February 21 to March 8 and for each block of 48 runs, for further analysis we kept the values that yielded the smaller fitting error over all runs. For the period February 21-March 8 which is used for the calibration of the model parameters, the median value of the ratio between the number of new cases of infected and recovered (excluding the zero values) is of the order of 10, while the average value of the ratio of the cumulative number of infected and deaths is of the order of 20 (excluding the zero values). Hence, we have used as weights w1=1, w2=10, w3=20 to balance for the different scales of the number of infected vs. the number of recovered and dead. Other reasonable choices for the values of the weights around these values resulted to similar outcomes.
For all the near-optimal points obtained using the genetic algorithm opti-mization, the residual was of the order of ∼ 4,750,000. Regarding the values of the optimal parameters, we fitted their cumulative probability distributions using several function including the Normal, Log-normal, Weibull, Beta, Gamma, Burr, Exponential and Birnbaum-Saunders functions and kept the one resulting the maximum Log-likelihood (see in the SI). Note that the optimal values of DAY-ZERO were between January 5 - January 23 (see Figure S1), the optimal values of β were between 0.63 and 0.9 (see Figure S2) and the optimal values of E were between 0.01 and 0.27 (see Figure S3). The best fit to the distribution of optimal values of the DAY-ZERO was obtained using a Normal CDF with mean 1.242 (days before the 16th of January) (95% CI:1.107, 1.377) and variance 4.417 (95% CI: 4.323, 4.514), while the mean value of the actual distribution was found to be 1.242; thus the expected DAY-ZERO corresponds to January 15. The best fit to the distribution of the optimal values of β, was given by fitting a Burr CDF with α = 0.654 (95% CI: 0.653, 0.654), c = 293.350 (261.419, 329.180), k = 0.0473 (95% CI: 0.0418, 0.0535) resulting to a mean value of 0.688 (95% CI: 0.680, 0.697); the mean value of the actual distribution was 0.705. Finally, the best fit to the distribution of the optimal values of E was given by fitting a Birnbaum-Saunders CDF with parameters µ = 0.0529 (95% CI: 0.0516, 0.054) (scale parameter) and α = 0.9314 (95% CI: 0.9112, 0.9515) (shape parameter), resulting to an expected value 0.0758 (see in SI) while the mean value of the actual distribution was found to be 0.0759.
Finally, to the Levenberg-Marquardt optimization algorithm (with finite difference step size 0.002), we have set as initial guesses the mean values of the actual distributions, i.e. DAY-ZERO was set as January 15, β=0.705 and E=0.0759. By doing so, the “effective” per-day transmission rate was found to be β = 0.686 (95% CI:0.660, 0.713), and E = 0.0609 (95% CI: 0.017, 0.105).
Based on the derived values of the “effective” per-day disease transmission rate, the basic reproduction number R0 is 4.51 (95% CI: 4.14, 4.90).
Using these estimated values for the epidemiological parameters, we ran the simulator from DAY-ZERO (15th of January) to March 8.
Figures (2),(3),(4) depict the simulation results based on the optimal estimates, starting from the most probable DAY-ZERO that is the 15th of January to the 8th of March. To validate the model with respect to the reported data of confirmed cases from March 9 to March 19, we have considered an 1-(1-0.5)(1-02) reduction in the “effective” transmission rate and as initial conditions the values resulting from the simulation on March 8 as described in the methodology. Thus, the model predicted fairly well the period from February 21 to March 19.
Cumulative number of (confirmed) infected cases resulting from simulations based on the results obtained by fitting the daily new cases (DAY-ZERO: January 15, β = 0.686 (95% CI:0.660, 0.713), and = 0.0609 (95% CI: 0.017, 0.105), until the 19th of March. The validation of the model was performed using the reported data of confirmed cases from March 9 to March 19 (shaded area) by taking 1-(1-0.5)(1-0.2) reduction in the “effective” transmission rate (see Methodology) to the lockdown of March 8. Dots correspond to the reported data of confirmed cases. Dotted lines depict the upper and lower limits of the estimation.
Cumulative number of (confirmed) recovered cases resulting from simulations based on the results obtained by fitting the daily new cases (DAY-ZERO: January 15, β = 0.686 (95% CI:0.660, 0.713), and = 0.0609 (95% CI: 0.017, 0.105), until the 19th of March. The validation of the model was performed using the reported data of confirmed cases from March 9 to March 19 (shaded area) by taking 1-(1-0.5)(1-0.2) reduction in the “effective” transmission rate (see Methodology) to the lockdown of March 8. Dots correspond to the reported data of confirmed cases. Dotted lines depict the upper and lower limits of the estimation.
Cumulative number of (confirmed) deaths resulting from simulations based on the results obtained by fitting the daily new cases (DAY-ZERO: January 15, β = 0.686 (95% CI:0.660, 0.713), and = 0.0609 (95% CI: 0.017, 0.105), until the 19th of March. The validation of the model was performed using the reported data of confirmed cases from March 9 to March 19 (shaded area) by taking 1-(1-0.5)(1-0.2) reduction in the “effective” transmission rate (see Methodology) to the lockdown of March 8. Dots correspond to the reported data of confirmed cases. Dotted lines depict the upper and lower limits of the estimation.
As discussed in the Methodology, we also attempted to forecast the evolution of the outbreak based on our analysis. To do so, based on the google data [25], we have considered a 1-(1-0.8)(1-0.2) reduction in the “effective” transmission rate β = 0.686 (95% CI:0.660, 0.713), starting on March 20, the day of announcement of even stricter measures in the region of Lombardy (see in Methodology). The result of our forecast is depicted in Figure 5 (lower and upper limits of the estimations are also shown). As it is shown, the model predicts fairly well the evolution of the epidemic. For On April 9, the upper bound of the simulations resulted to ∼53,810 “confirmed” infected cases while the reported cumulative number of confirmed cases was ∼54,800. For the same day, the model predicted as an upper bound ∼ 11,400 deaths while the reported number of deaths was 10,022. Thus, the reported cases are within the model predictions one month after March 8 (the model parameters and the DAY-ZERO were estimated using the reported data from February 21 to March 8). As predicted by the simulations, if the strict isolation measures continue to hold, the outbreak in Lombardy is expected to fade out by end of May-early June, 2020.
Estimated number of the actual infected cases in the total population (red thin solid line), the estimated cumulative number of “confirmed” infected cases (red thick solid line) and the estimated deaths (thick black line) per day resulting from simulations from March 8 (the day of the lockdown of all Italy) to June 15. Based on the Google released data (see in Methodology), we considered a 1-(1-0.5)(1-0.2) reduction of the “effective” transmission rate (β = 0.686 (95% CI:0.660, 0.713)) until March 19 (based on the drop in the mobility in Lombardy as estimated by real mobile phone data and the effect of social distancing), and then considering a 1-(1-0.8)(1-0.2) reduction due to the even stricter mobility limitation measures announced by the government on March 20 and March 21. Dotted lines depict the upper and lower limits of the estimation. Red and black dots correspond to the reported data (up to April 9, 2020) of confirmed infected cases and deaths, respectively.
Discussion
The crucial questions about an outbreak is how, when (DAY-ZERO), why it started, and when it will end. Answers to these important questions would add critical knowledge in our arsenal to combat the pandemic. The tracing of DAY-ZERO, in particular, is of outmost importance. It is well known that minor perturbations in the initial conditions of a complex system, such as the ones of an outbreak, may result in major changes in the observed dynamics. No doubt, a high level of uncertainty for DAY-ZERO, as well as the uncertainty in the actual numbers of exposed people in the total population, raise several barriers to our ability to correctly assess the state and dynamics of the outbreak, and to forecast its evolution and its end. Such pieces of information would lower the barriers and help public health authorities respond fast and efficiently to the emergency.
This study aimed exactly at shedding more light into this problem, taking advantage of state-of-the-art tools of mathematical modelling and numerical analysis/optimization tools. To achieve this goal, we addressed a compartmental SEIRD model with two infectious compartments in order to bridge the gap between the number of reported cases and the actual number of cases in the total population.
By following the proposed methodological framework, we found that the DAY-ZERO in Lombardy was around the mid of January, a date that precedes by one month the fate of the first confirmed case in the hardest-hit northern Italian region of Lombardy. Furthermore, our analysis revealed that the actual cumulative number of infected cases in the total population in the period until March 8 was around 15 times the cumulative number of confirmed infected cases. Interestingly enough, regarding the estimation of the DAY-ZERO of the outbreak in Lombardy, a very recent study based on genomic and phylogenetic analyses reports the same time period, between the second half of January and early February, 2020, as the time when the novel coronavirus SARS-CoV-2 entered northern Italy, [33].
Regarding the forecasting of the fade out of the pandemic in the region of Lombardy, we have taken into account the very latest facts on the drop of human mobility, as released by Google [25] on March 29 for the region of Lombardy, shaped by the new draconian measures announced on March 20-21 that include the closure of all parks, public and private offices and the prohibition of any pedestrian activity, even individually [31]. We predict that the COVID-19 pandemic in Lombardy will fade out by the end of May-early June, 2020, if the draconian, as of March 20-21, social isolation measures are implemented and maintained.
To this end, we would like to make a final comment with respect to the basic reproduction number R0, the significance and meaning of which are very often misinterpreted and misused, thereby leading to erroneous conclusions. Here, we found a R0 ∼ 4.5, which is higher compared to the values reported by many studies in China. For example, Zhao et al. estimated R0 to range between 2.24 (95% CI: 1.96, 2.55) and 3.58 (95% CI: 2.89, 4.39) in the early phase of the outbreak [8]. Similar estimates were obtained for R0 by Imai et al., 2.6 (95% CI: 1.5, 3.5) [5], Li et al. [34], Wu et al., 2.68 (95% CI: 2.47, 2.86), as well as by Anastassopoulou et al. recently, 3.1 (90% CI: 2.5, 3.7) [7].
However, we would like to stress that R0 is NOT a biological constant for a disease as it is affected not only by the pathogen, but also by many other factors, such as environmental conditions, the demographics, as well as, importantly, by the social behavior of the population (see for example the discussion in [35]). Thus, a value for R0 that is found in a part of the world (and even in a region of the same country) cannot be generalized as a global biological constant for other parts of the world (or even for other regions of the same country). Obviously, the environmental factors and social behavior of the population in Lombardy are different from the ones, for example, prevailing in Hubei.
We hope that the results of our analysis help to mitigate some of the severe consequences of the currently uncontrolled pandemic.
Data Availability
All data referred to in the manuscript are provided as supplementary information.
Conflict of Interest
The authors declare no conflict of interest.
Funding
We did not receive any specific funding for this study.
Data Availability
The data used in this paper are given in the Supporting information.
Author Contributions
Constantinos Siettos performed the formal numerical analysis and computations. Lucia Russo contributed to the development of the model and the formal analysis. Gennaro Nicola Bifulco analysed and collected the data. Gerardo Toraldo and Emilio Fortunato Campana contributed to the numerical analysis and optimization procedure. Cleo Anastassopoulou and Athanassios Tsakris interpreted the epidemiological meaning of the results. Constantinos Siettos, Cleo Anastassopolou and Lucia Russo wrote the manuscript. All authors reviewed the manuscript.
Supporting information
Data
All the relevant data used in this paper are publicy available and accessible at https://lab.gedidigital.it/gedi-visual/2020/coronavirus-i-contagi-in-italia/. The reported cumulative numbers of cases from Febrary 21 to March 19 are listed in Table S1. The data from February 21 to March 8 have been used for the calibration of the model parameters and the data from March 9 to March 19 have been used for the validation of the model.
Reported cumulative numbers of cases for Lombardy, Italy (February 21-March 19)
Fitting the Distributions of the Optimal Values
We fitted the cumulative probability distributions of DAY-ZERO β, ϵ using several functions including the Normal, Log-normal, Weibull, Beta, Gamma, Burr, Exponential and Birnbaum-Saunders CDFs and kept the one resulting in the maximum Log-likelihood. For the DAY-ZERO, the best fit to the distribution of the optimal values was obtained by the Normal CDF:
with mean value µ = 1.2423 (95% CI: 1.107, 1.377) and σ = 0.4169 (95% CI:4.323, 4.514).
The cumulative distribution of DAY-ZERO and the resulting exponential distribution are given in Figure S1.
For the distribution of β values the best fitting distribution was obtained by the Burr CDF which is a three-parameter family of curves given by:
with α = 0.654 (95% CI: 0.653, 0.654), c = 293.35 (95% CI: 261.419, 329.18), k = 0.0473 (95% CI: 0.0418, 0.0535). Thus, the resulting mean value is β = 0.688(95%CI : 0.6800.698) while the mean value of the actual distribution is 0.705. The cumulative distribution of beta and the resulting Burr CDF distribution are given in Figure S2.
For ϵ, the best fit to the distribution of the optimal values was obtained by a Birnbaum-Saunders CDF:
with µ = 0.0529 (95% CI: 0.0516, 0.054) (scale parameter) and α = 0.9314 (95% CI: 0.9112, 0.9515) (shape parameter). Φ(x) denotes the standard normal CDF. The mean value is given by:
Cumulative probability distribution of the optimal values of DAY-ZERO as obtained by running the optimization problem using a grid of 20 × 13 × 15 initial guesses, thus using a 2 days step for the DAY-ZERO within the interval 27 December 2019-5th of February 2020 i.e. ±20 days around the 16th of January, a step of 0.05 within the interval (0.3, 0.9) for β and a step of 0.02 within the interval (0.01, 0.29) for ϵ =. The best fit was obtained with the Normal CDF with µ = 1.242 (95% CI: 1.107, 1.378) (thus corresponding to the 15th of January) and σ = 4.4169 (95% CI:4.323, 4.514); the mean values of the actual distribution was 1.242.
Cumulative probability distribution of the optimal values of β as obtained by running the optimization problem using a grid of 20 × 13 × 15 initial guesses, thus using a 2days step for the DAY-ZERO within the interval 27 December 2019-5th of February 2020 i.e. ±20 days around the 16th of January, a step of 0.05 within the interval (0.3, 0.9) for β and a step of 0.02 within the interval (0.01, 0.29) for ϵ. The best fit was obtained with the Burr CDF, with α = 0.6542 (95% CI: 0.6537, 0.6547), c = 293.35 (261.419, 329.18), k = 0.0473 (95% CI: 0.0418, 0.0535).
Cumulative probability distribution of the optimal values of as obtained by running the optimization problem using a grid of 20 × 13 × 15 initial guesses, thus using a 2days step for the DAY-ZERO within the interval 27 December 2019-5th of February 2020 i.e. ±20 days around the 16th of January, a step of 0.05 within the interval (0.3, 0.9) for β and a step of 0.02 within the interval (0.01, 0.29) for ϵ. The best fit was obtained by a Birnbaum-Saunders CDF, with µ = 0.0529 (95% CI: 0.0516, 0.0543) (scale parameter) and α = 0.9314 (95% CI: 0.9112, 0.9515) (shape parameter).
Thus, the mean value is given by ϵ = 0.0758 (95% CI: 0.0730, 0.0788), while that of the actual distribution is 0.0759.
The cumulative distribution of ϵ and the resulting exponential distribution are given in Figure S3.
References
