Modelling the epidemic 2019-nCoV event in Italy: a preliminary note

A. The SEIR model and its limiting approximation

In the SEIR framework [5], individuals in the population are classified according to their infectious status: Susceptible (S), Exposed (E) (infected but not infectious), Infectious (I) and Recovered (R). In the case of a new infection (as in the present case) the population has no prior immunity, consequently the population starts out at the disease-free equilibrium (S ≈N, E = 0, I = 0, R = 0), where N is the total population size, and the dynamics are determined by the following equations describing the rates of change of each simplified classes:

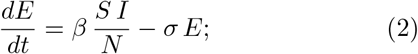
After introduction of an infectious individual (and if the basic reproductive ratio, R₀ = β/γ, is greater than 1), the infection develops through the population by contacts between susceptible and infected individuals to sustain further transmission. Neglecting background birth and death processes (because of the short period analyzed w.r.t. the typical vital periods), the population eventually reaches the following state (S = S_∞, E = 0, I = 0, R = N − S_∞), where S_∞ is defined as the solution to R₀(S_∞/N − 1) = ln(S_∞/N) for large N.

The SIR model is a limiting case of the previous framework and assumes E + I → I at any time, without distinguishing the classes E and I. The previous equations reduce to

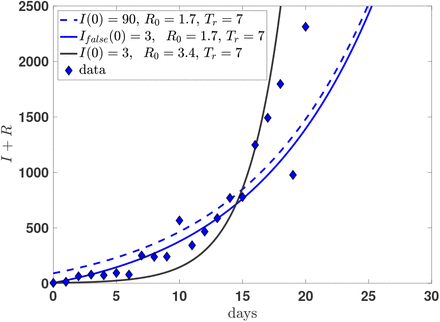
In Fig. 1 we show the available data [6, 7] for the initial period February 20th - March 11th (21 days) and their comparison with the simplest SIR approximation (5), (6), and (7) (iteratively solved by means of a MATLAB code) for a first intuitive analysis.

• Download figure
• Open in new tab

FIG. 1.

(color on line). The data cases as detected in Italy in the period February 20th (day=0) and March 11th (day = 20) (Ministero della Salute [6, 7]), compared with the prediction of few deterministic models, see text.

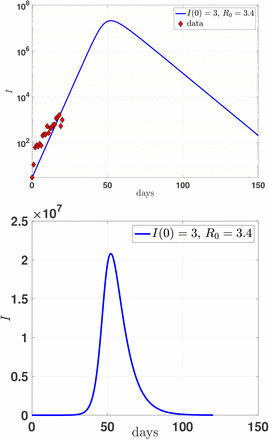
The continuous black curve shows the solution assuming a I(0) = 3 number of infectious individuals at day=0, exactly equivalent to the official detected cases at the same day. No attention is paid to a best fit of the data, also because they are rather sparse, however the quality of the simple (SIR) model is evident also at the first stages of the epidemic. The parameter values sound also reasonable: with a recovering average time T_r = 7 days (γ = 1/T_r) and R₀ = 3.4 and no further corrections: a brilliant example of the predictive force of the SIR model. However Fig. 1 has a more specific aim: showing the rather delicate rôle played by a possible underestimation of the infectious individual at the early stages of the infection outbreak. In fact one can assumes a different (possible) scenario based on the difficulty of a precise estimation of the initial number of infectious individuals. Such a possible scenario is illustrated by the the full blue curve showing a prediction which results from a misleading estimation of I(0). The effective number of initial infectious is 30 times larger (I(0) = 90), but the curve has been translated to a fictitious Ī(0) = 3, the reveled number, from the dashed mathematical result. A change in R₀ from R₀ = 3.4 to R₀ = 1.7 would give a reasonable fit of the early stage of the outbreak. The effect is rather well known as discussed in ref. [8] in the case of the epidemic event in China. In that case a proposed exponential fit of the precocious data (January 10th to January 24th) results in a values of R₀ ≈3.58 which is reduced to R₀ ≈2.24 is the associated initial condition on I(0) is multiplied by an increasing factor from 2 to 8. In Fig. 2 we show the time behavior of the infectious population within the simple SIR model of Eqs. (5)-(7) (T_r = 1/γ = 7 days, R₀ = 3.4) both in logarithmic (upper panel) and linear scale (lower panel). The data are the data of Fig. 1.

• Download figure
• Open in new tab

FIG. 2.

(color on line) upper panel Behavior (in logarithmic scale) of the number of infectious individuals in Italy within the SIR model and the comparison with available data till March 11th, 2020. lower panel: As in the upper panel but in linear scale to better appreciate the global behavior and the effective time to recover.

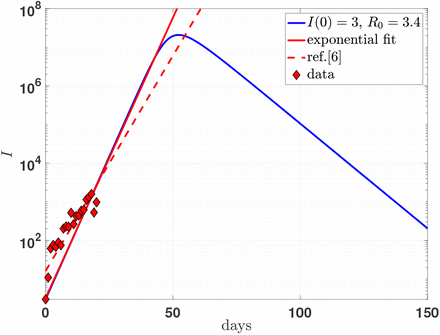
The exponential behavior predicted by the model in the growing part of the outbreak description is evident and can be compared with the recent fit to the data by

Bucci and Marinari in ref. [9]. While the present simplified SIR model predict a doubling infectious population each (roughly) 2 days, the Roma fit [9] gives an estimation of 2.6 days (see Fig. 3).

• Download figure
• Open in new tab

FIG. 3.

(color on line). The model predictions of Fig. 2 are compared with an exponential fit (full red line) I ∼ exp (t_days/2.994) and compared with the fit proposed in ref.[9] (dashed red line).

B. A Quarantined model with isolation

The model [4] is a generalized SEIR-type epidemiological model which incorporates appropriate compartments relevant to intervention such as quarantine, isolation and treatment. The population is stratified in Susceptible (S), exposed (E), infectious but not yet symptomatic (pre-symptomatic) (A), infectious with symptoms (I), hospitalized (H) and recovered (R). Further stratification includes quarantined susceptible (S_q), isolated exposed (E_q) and isolated infected (I_q) compartments. The equations of the model are explicitly shown in Eqs. (8)-(15).

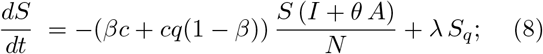
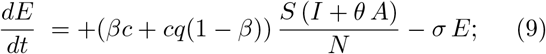
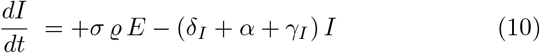
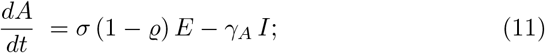
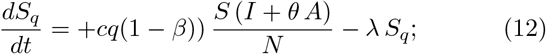
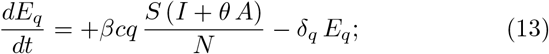
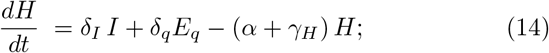
The authors of ref. [4] have calibrated the model on the data of the 2019-nCoV as emerged in Wuhan the last two months, therefore in a situations that has the same basic parameters. In table I the values of the model parameters as tuned by Tang et al. on the outbreak event at Wuhan are summarized and the initial conditions imposed to the solutions of the Eqs. (8)-(15) are summarized in table II for the populations localized in Wuhan and in Italy.

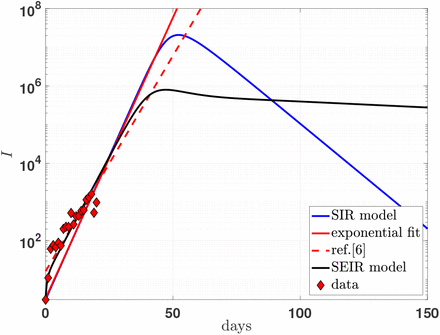
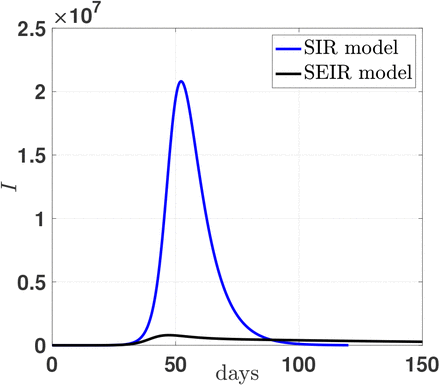
The results are shown in Figs 4 and 5. The drastic reduction of the infectious population is evident as well as the long tail of the distribution.

• Download figure
• Open in new tab

FIG. 4.

(color on line). Number of infectious individuals for the 2019-nCoV outbreak in Italy. The SEIR model predictions (full black line) are compared with the simplified results of the SIR model of Fig. 3 as well as the proposed exponential fit of Bucci and Marinari [9] (see Figure caption). The maximum values are drastically reduced, at the cost of a long tail in the distribution.

• Download figure
• Open in new tab

FIG. 5.

(color on line). The time evolution of the infectious population in the Italian outbreak. The linear scale emphasize the drastic reduction induced by isolation, quarantine and intense tracing as described by the recent formulation of a SEIR model based on the Wuhan database (see ref. [4]).

The quarantine imposed to the infectious individuals, the effects of an intensive contact tracing and isolation reduce the maximum value of the distribution by a factor ∼ 26 (see Fig. 5).