Epidemiological parameter review and comparative dynamics of influenza, respiratory syncytial virus, rhinovirus, human coronavirus, and adenovirus

Julie A. Spencer, Deborah P. Shutt, Sarah K. Moser, Hannah Clegg, Helen J. Wearing, Harshini Mukundan, Carrie A. Manore
doi: https://doi.org/10.1101/2020.02.04.20020404

Abstract

Influenza-like illness (ILI) accounts for a large burden of annual morbidity and mortality worldwide. A finer-grained knowledge of the parameters and dynamics of the viruses commonly underlying ILI is needed for modeling, diagnostic, and intervention efforts. We conducted an extensive literature review for epidemiological parameter values for influenza, respiratory syncytial virus (RSV), rhinovirus, human coronavirus (HCoV), and adenovirus. We also developed a deterministic SEIR model for ILI, and derived an expression for R0. We here report ranges and means for parameters for these five common viruses.

1 Introduction

Influenza-like illness (ILI) accounts for a large burden of annual morbidity and mortality worldwide (WHO 2020). Despite this, diagnostic testing for specific viruses underlying ILI is relatively rare (CDC 2019). This results in a lack of information about the pathogens that make between 9 million and 49 million people sick every year in the United States alone (CDC 2020). Yet knowledge of the specific diseases is necessary for timely treatment to prevent unnecessary suffering and death (Nguyen 2016, Van Asten et al. 2012, Pawelek et al. 2015).

ILI is defined by the CDC as fever of 100°F and a cough and/or a sore throat without a known cause other than influenza (CDC 2020). Defining ILI as a cluster of symptoms rather than a specific disease or diseases is necessary for keeping track of case counts, as well as for important analysis and forecasting (Osthus and Moran 2019). However, the cluster of symptoms known as ILI is caused by many under-lying pathogens (Taylor 2017, Galindo-Fraga 2013). Positive diagnosis is a prerequisite for accurate treatment. To respond to this need and to gain a finer-grained understanding of ILI that will contribute to a practical foundation for advances in diagnostics and interventions, we here review the literature for parameter values. We then compare the dynamics of five common upper respiratory viruses implicated in ILI: influenza, respiratory syncytial virus (RSV), rhinovirus, human coronavirus (HCoV), and adenovirus.

We conducted a literature review to establish plausible ranges for model parameters, and developed a deterministic system of ordinary differential equations to model the general dynamics of these five viruses.

2 Results of Parameter Literature Review

2.1 ILI Viruses

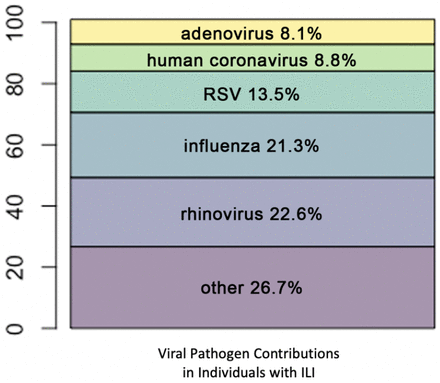
We reviewed the literature for the epidemiological parameters: incubation period, infectious period, hospitalization period, hospitalized proportion, case fatality proportion, and R0. We included results from experimental and observational studies, as well as from systematic reviews when there were insufficient studies. R0 values were estimated from modeling studies. In one case, (SARS-hCoV), we included an estimate for the infectious period, since values were lacking in the literature (Chowell 2004). We also searched the literature for the contribution made by each of the five viruses to the total viral community in people with ILI. Across ten study populations, at least one virus was identified in an average of 62% of individuals with ILI symptoms. Out of these 62% of patients with ILI in whom viruses have been identified, adenovirus was identified in 8.1% of samples, human coronavirus in 8.8%, RSV in 13.5%, influenza in 21.3%, and rhinovirus in 22.6%. Coinfection was not taken into account in these estimates.

View this table:
Table 1:

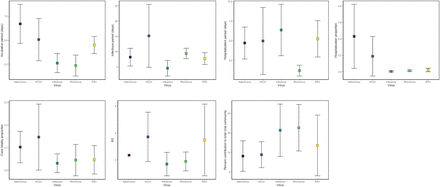
Parameters for Influenza-like illness

2.2 Human Coronavirus

View this table:
Table 2:

Parameters for HCoV

In view of the current outbreak of novel coronavirus 2019-nCoV, and given the need for plausible parameters for modeling efforts, we conducted an in-depth literature review for human coronavirus. 2019-nCoV has been identified as a member of genus betacoronavirus, along with SARS and MERS (WHO 2020). Until the genomes of 2019-nCoV have been further characterized, it seems reasonable to suspend assumptions about the epidemiological behavior of the novel virus, and to include all known strains in the parameter sets. Thus, our review includes values for strains 229E, NL63, OC43, HKU1, SARS, and MERS. Means have been collected when possible; when not available, medians have been recorded. Information on the studies, the strains, the sample sizes, and the references is available on pages 26-27 of this paper.

We included values for R0 only for SARS and MERS, and attempted to include them only for the period before large-scale interventions were implemented, since R0 is defined as the average number of sec-ondary infections produced when one infected individual is introduced into a fully susceptible population (K. Deitz, 1975). Since the seasonal strains of human coronavirus are endemic in the world, there is, by definition, no fully susceptible population for 229E, NL63, OC43, or HKU1 in which R0 may be assessed.

Results of our review for human coronavirus include the following mean values: an incubation period of 5.01 days, an infectious period of 15.2 days, a hospitalization period of 4.96 days, a hospitalized proportion of 0.188, a case fatality proportion of 0.147, and an R0 of 3.7.

3 Deterministic Model

3.1 Description of Model Structure

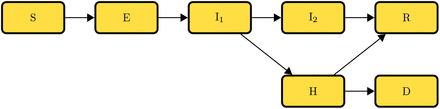
The model diagram (Fig.1) illustrates the progression of influenza-like illness (ILI) in a human population of a hypothetical small city containing 10,000 individuals. We assume density-dependence, that is, for a fixed population of 10,000 humans with negligible migration, the contact rate for individuals remains constant.

Figure 1:
Figure 1:

Viral Composition

Figure 2:
Figure 2:

Transfer diagram for ILI virus transmission.

The total population (N) consists of seven classes: susceptible (S), exposed but not infectious (E), first infectious class (I1), second infectious class (I2), hospitalized (H), recovered (R), or dead (D). Individ-uals are considered susceptible until they contact an infectious individual from (I1), (I2), or (H). Given contact with an infectious individual, transmission takes place with some probability. After transmission of the virus has occurred, susceptible people move to the exposed class (E), where they spend a number of days equal to the mean period of time between infection and the onset of infectiousness (the latent period). We assume here that the latent period equals the incubation period, or the mean period of time between exposure to the virus and the onset of symptoms. After the latent period, they move to the first infectious class (I1). The mean duration of the first infectious period differs according to the underlying virus. Symptoms worsen for some proportion of the first infectious class, who enter the hospital (H), where they remain infectious. Individuals who do not enter the hospital remain ill outside the hospital for the duration of the second infectious period (I2). From (I2), the length of which differs according to the underlying virus, where we assume that the progression of the illness is not severe, individuals recover. The duration of hospitalization differs according to the underlying virus. From the hospital, individuals either recover (R) or die (D). We assume that hospitalized individuals have 75% less contact with susceptible individuals, which results in 75% reduced transmission during hospitalization. We further assume that recovered individuals (R) gain full immunity to the virus causing the illness.

View this table:
Table 3:

Descriptions of state variables

Model assumptions include:

  1. From the initially infectious state, individuals progress to hospital or continued non-hospitalized infectious state.

  2. From the non-hospitalized infectious state, individuals progress to recovery.

  3. From the hospitalized state, individuals progress to death or recovery.

  4. Everyone who recovers gains full immunity.

  5. Total infected population = E + I1 + I2 + H.

  6. Total infectious population = I1 + I2 + H.

  7. The viruses operate independently.

  8. The population is homogeneously mixed.

  9. No demographics are included.

  10. The transmission rate for each virus is calculated from the expression for R0 below, using the mean R0 values from the literature.

View this table:
Table 4:

Descriptions and dimensions for parameters

3.2 Model Equations

The equations governing common upper respiratory virus dynamics are given by Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image

The total population is N = S + E + I1 + I2 + H + R + D. Parameters

4. Quantities of Interest

4.1 Disease-free Equilibrium

We assume that the stable population, representing a hypothetical small city, is N = 10000. We further assume that the initial value for the Susceptible population is S0 = 10000. In the disease-free state, all infected classes are zero,that is, E = I1 = I2 = H = 0. Substituting and setting the derivatives equal to zero, it is evident that in the disease-free state, the other state variables R and D will continue to contain zero individuals, and that the Susceptible class S will remain equal to the total population N, as follows. 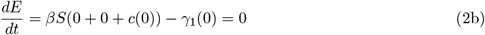Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image

Additionally, if we set any one of E, I1, I2, or H to zero, the other three state variables representing infected classes must also be zero. In this case, N=S=10000. Thus, where x = (S, E, I1, I2, H, R, D) denotes solutions of the system, xdfe = (10000, 0, 0, 0, 0, 0, 0) represents the disease-free equilibrium for the system.

4.2 Basic Reproduction Number

Assuming a homogeneously mixed population, the basic reproductive number (R0) is defined as the average number of secondary infections produced when one infected individual is introduced into a fully susceptible population (K. Dietz, 1993). Four compartments, latently infected individuals (E), symptomatic and infected individuals (I1), symptomatic and infected and non-hospitalized individuals (I2), and hospitalized individuals (H), together characterize the total infected population for the ILI virus system. To calculate R0 for this system, we derive the next generation matrix (Van den Driessche and Watmough 2002).

Method:

  1. Derive the matrix for the transmission term describing everyone entering (E): the “F” matrix;

  2. Derive the matrix for the transition terms describing everyone transitioning between infected classes (E, I1, I2, H): the “V” matrix;

  3. Next Generation Matrix (NGM) = (F)(V −1);

  4. The largest dominant eigenvalue or spectral radius of the NGM = R0 for the system. The transmission term for the system is βS(I1 + I2 + cH)

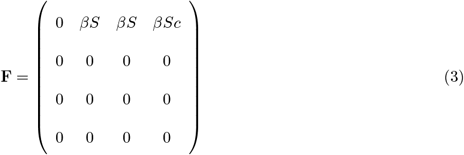
Embedded Image

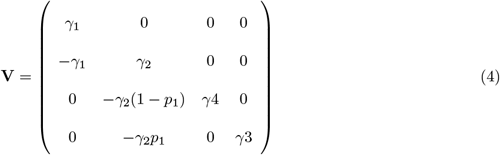
The transmission terms for the system are (−γ1E), (γ1E − γ2I1), (γ2(1 − p1)I1 − γ4I2), (γ2p1I1 − γ3H). Embedded Image

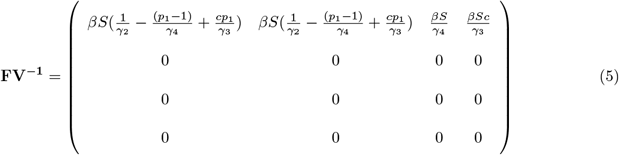
The next generation matrix is Embedded Image

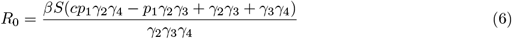
The spectral radius, or the largest positive eigenvalue of the next generation matrix, is the basic reproductive number of the system at the disease-free equilibrium, as follows. Embedded Image

This expression for the basic reproductive number (R0) depends on the parameters β, c, p1, γ2, γ3 and γ4, and on the initial conditions for the state variables. β is clearly directly proportional to R0.

CONCEPTUAL METHOD OF DERIVING R0

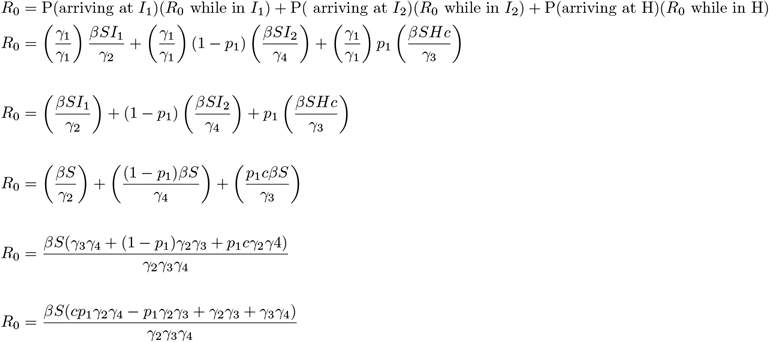
Embedded Image

This result is equivalent to the result obtained, above, by the next generation method.

5. Discussion

There are several limitations to this study. First, the model is not age-structured. Second, the assumption that the latent period equals the incubation period may result in an overestimation of the latent period. This is because the beginning of the true infectious period may occur before the onset of symptoms; however, this is difficult to measure and is not generally reported in the studies that report values for the incubation period. Third, a single mortality rate has been modeled for the hospitalized infected and non-hospitalized infected classes. Fourth, many of the studies that generated parameter values evaluated populations treated at clinics or admitted at hospitals. However, a significant proportion of illness and death may occur outside of hospitals and clinics (see Cohen et al. 2017).

Much work remains to be done to elucidate the etiology of ILI.

Data Availability

The plots and spreadsheets that contain the details of our parameter review are included in the paper, after the reference section.

FUNDING STATEMENT

Research support provided by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). LA-UR-20-21024.

JAS was partially funded by the University of New Mexico College of Arts and Sciences Dissertation Excellence Fellowship.

ILI Parameter Ranges and Means

Figure

INFLUENZA parameters: incubation period, infectious period, hospitalization period, hospitalization proportion, case fatality, R0

View this table:

RSV parameters: incubation period, infectious period, hospitalization period, hospitalization rate, case fatality rate, R0

View this table:

ADENOVIRUS parameters: incubation period, infectious period, hospitalization period, reduction of transmission in hospital, hospitalization rate, case fatality rate, R0

NOTE: adenovirus in the elderly produces keratoconjunctivitis, not a respiratory infection

View this table:

HUMAN CORONAVIRUS parameters: incubation period, infectious period, onset of symptoms to hospitalization, hospitalization period, hospitalization proportion, case fatality, R0

View this table:

RHINOVIRUS parameters: incubation period, infectious period, hospitalization period, hospitalization proportion, case fatality, R0

View this table:

6 References

  1. Al-Tawfiq, J.A., Hinedi, K., Ghandour, J., Khairalla, H., Musleh, S., Ujayli, A. and Memish, Z.A., 2014. Middle East respiratory syndrome coronavirus: a case-control study of hospitalized patients. Clinical Infectious Diseases, 59(2), pp.160–165.
    OpenUrlCrossRefPubMed
  2. Alonso, W.J., Viboud, C., Simonsen, L., Hirano, E.W., Daufenbach, L.Z. and Miller, M.A., 2007. Seasonality of influenza in Brazil: a traveling wave from the Amazon to the subtropics. American journal of epidemiology, 165(12), pp.1434–1442.
    OpenUrlCrossRefPubMedWeb of Science
  3. Ang, L.W., Lim, C., Lee, V.J.M., Ma, S., Tiong, W.W., Ooi, P.L., Lin, R.T.P., James, L. and Cutter, J., 2014. Influenza-associated hospitalizations, Singapore, 2004–2008 and 2010–2012. Emerging infectious diseases, 20(10), p.1652.
    OpenUrl
  4. Arruda, E., Pitkäranta, A.N.N.E., Witek, T.J., Doyle, C.A. and Hayden, F.G., 1997. Frequency and natural history of rhinovirus infections in adults during autumn. Journal of clinical microbiology, 35(11), pp.2864–2868.
    OpenUrlAbstract/FREE Full Text
  5. Assiri, A., Al-Tawfiq, J.A., Al-Rabeeah, A.A., Al-Rabiah, F.A., Al-Hajjar, S., Al-Barrak, A., Flemban, H., Al-Nassir, W.N., Balkhy, H.H., Al-Hakeem, R.F. and Makhdoom, H.Q., 2013. Epidemiological, demographic, and clinical characteristics of 47 cases of Middle East respiratory syndrome coronavirus disease from Saudi Arabia: a descriptive study. The Lancet infectious diseases, 13(9), pp.752–761.
    OpenUrlCrossRefPubMedWeb of Science
  6. Avendano, L.F., Palomino, M.A. and Larranaga, C., 2003. Surveillance for respiratory syncytial virus in infants hospitalized for acute lower respiratory infection in Chile (1989 to 2000). Journal of clinical microbiology, 41(10), pp.4879–4882.
    OpenUrlAbstract/FREE Full Text
  7. Avila, PC, Abisheganaden, JA, Wong, H, Liu, J, Yagi, S, Schnurr, DS, Kishiyama, JL, Boushey, HA, 2009. Effects of allergic inflammation of the nasal mucosa on the severity of rhinovirus 16 cold. Journal of Allergy and Clinical Immunology, 105(5), 923–931.
    OpenUrl
  8. Bastien, N., Anderson, K., Hart, L., Caeseele, P.V., Brandt, K., Milley, D., Hatchette III, T., Weiss, E.C. and Li, Y., 2005. Human coronavirus NL63 infection in Canada. The Journal of infectious diseases, 191(4), pp.503–506.
    OpenUrlCrossRefPubMedWeb of Science
  9. Bauch, C.T., Lloyd-Smith, J.O., Coffee, M.P. and Galvani, A.P., 2005. Dynamically modeling SARS and other newly emerging respiratory illnesses: past, present, and future. Epidemiology, pp.791–801.
  10. Berger, S., 2010. Infectious Diseases of Bhutan 2010 edition. “O’Reilly Media, Inc.”.
  11. Biggerstaff, M., Cauchemez, S., Reed, C., Gambhir, M. and Finelli, L., 2014. Estimates of the reproduction number for seasonal, pandemic, and zoonotic influenza: a systematic review of the literature. BMC infectious diseases, 14(1), p.480.
    OpenUrlCrossRefPubMed
  12. Boivin, G., Baz, M., Côté, S., Gilca, R., Deffrasnes, C., Leblanc, É., Bergeron, M.G., Déry, P. and De Serres, G., 2005. Infections by human coronavirus-NL in hospitalized children. The Pediatric infectious disease journal, 24(12), pp.1045–1048.
    OpenUrlCrossRefPubMedWeb of Science
  13. Bollaerts, K., Antoine, J., Van Casteren, V., Ducoffre, G., Hens, N. and Quoilin, S., 2013. Contribution of respiratory pathogens to influenza-like illness consultations. Epidemiology Infection, 141(10), pp.2196–2204.
    OpenUrl
  14. Bradburne, A.F., Bynoe, M.L. and Tyrrell, D.A., 1967. Effects of a” new” human respiratory virus in volunteers. British medical journal, 3(5568), p.767.
    OpenUrlFREE Full Text
  15. Broor, S., Dawood, F.S., Pandey, B.G., Saha, S., Gupta, V., Krishnan, A., Rai, S., Singh, P., Erdman, D. and Lal, R.B., 2014. Rates of respiratory virus-associated hospitalization in children aged¡ 5 years in rural northern India. Journal of Infection, 68(3), pp.281–289.
    OpenUrl
  16. Buecher, C., Mardy, S., Wang, W., Duong, V., Vong, S., Naughtin, M., Vabret, A., Freymuth, F., Deubel, V. and Buchy, P., 2010. Use of a multiplex PCR/RT-PCR approach to assess the viral causes of influenza-like illnesses in Cambodia during three consecutive dry seasons. Journal of medical virology, 82(10), pp.1762–1772.
    OpenUrlCrossRefPubMed
  17. ↵
    CDC, “Glossary,” https://www.cdc.gov/flu/about/glossary.htm, accessed on 1/28/2020.
  18. CDC, “RSV Transmission,” https://www.cdc.gov/rsv/about/transmission.html Ȧccessed on 1/28/2020.
  19. CDC, “U.S. Influenza Surveillance System: Purpose and Methods”, https://www.cdc.gov/flu/weekly/overview.htm, accessed on 1/28/2020.
  20. Chadha, M.S., Broor, S., Gunasekaran, P., Potdar, V.A., Krishnan, A., Chawla-Sarkar, M., Biswas, D., Abraham, A.M., Jalgaonkar, S.V., Kaur, H. and Klimov, A., 2012. Multisite virological influenza surveillance in India: 2004–2008. Influenza and other respiratory viruses, 6(3), pp.196–203.
    OpenUrl
  21. Chang, H.J., 2017. Estimation of basic reproduction number of the Middle East respiratory syndrome coronavirus (MERS-CoV) during the outbreak in South Korea, 2015. Biomedical engineering online, 16(1), p.79.
    OpenUrl
  22. Chiu, S.S., Chan, K.H., Chen, H., Young, B.W., Lim, W., Wong, W.H.S. and Peiris, J.M., 2010. Virologically confirmed population-based burden of hospitalization caused by respiratory syncytial virus, adenovirus, and parainfluenza viruses in children in Hong Kong. The Pediatric infectious disease journal, 29(12), pp.1088–1092.
    OpenUrlCrossRefPubMed
  23. Chiu, S.S., Hung Chan, K., Wing Chu, K., Kwan, S.W., Guan, Y., Man Poon, L.L. and Peiris, J.S.M., 2005. Human coronavirus NL63 infection and other coronavirus infections in children hospitalized with acute respiratory disease in Hong Kong, China. Clinical infectious diseases, 40(12), pp.1721–1729.
    OpenUrlCrossRefPubMedWeb of Science
  24. ↵
    Chowell, G., Viboud, C., Simonsen, L., Miller, M. and Alonso, W.J., 2010. The reproduction number of seasonal influenza epidemics in Brazil, 1996–2006. Proceedings of the Royal Society B: Biological Sciences, 277(1689), pp.1857–1866.
    OpenUrlCrossRefPubMed
  25. Chowell, G.M.A.M., Miller, M.A. and Viboud, C., 2008. Seasonal influenza in the United States, France, and Australia: transmission and prospects for control. Epidemiology Infection, 136(6), pp.852–864.
    OpenUrlCrossRefPubMedWeb of Science
  26. ↵
    Cohen, C., Walaza, S., Treurnicht, F.K., McMorrow, M., Madhi, S.A., McAnerney, J.M. and Tempia, S., 2017. In-and out-of-hospital mortality associated with seasonal and pandemic influenza and respiratory syncytial virus in South Africa, 2009–2013. Clinical Infectious Diseases, 66(1), pp.95–103.
    OpenUrl
  27. Commission on Acute Respiratory Diseases, 1947. Experimental transmission of minor respiratory illness to human volunteers by filter-passing agents. I. Demonstration of two types of illness characterized by long and short incubation periods and different clinical features. Journal of Clinical Investigation, 26(5), pp.957–973.
    OpenUrlCrossRefPubMedWeb of Science
  28. Corman, V.M., Albarrak, A.M., Omrani, A.S., Albarrak, M.M., Farah, M.E., Almasri, M., Muth, D., Sieberg, A., Meyer, B., Assiri, A.M. and Binger, T., 2016. Viral shedding and antibody response in 37 patients with Middle East respiratory syndrome coronavirus infection. Clinical Infectious Diseases, 62(4), pp.477–483.
    OpenUrlCrossRefPubMed
  29. Couch, R.B., Gordon Douglas Jr, R., Fedson, D.S. and Kasel, J.A., 1971. Correlated studies of a recombinant influenza-virus vaccine. III. Protection against experimental influenza in man. Journal of Infectious Diseases, 124(5), pp.473–480.
    OpenUrlCrossRefPubMedWeb of Science
  30. Cowling, B.J., Fang, V.J., Riley, S., Peiris, J.M. and Leung, G.M., 2009. Estimation of the serial interval of influenza. Epidemiology (Cambridge, Mass.), 20(3), p.344.
    OpenUrlCrossRefPubMedWeb of Science
  31. de Blasio, B.F., Iversen, B.G. and Tomba, G.S., 2012. Effect of vaccines and antivirals during the major 2009 A (H1N1) pandemic wave in Norway–and the influence of vaccination timing. PLoS One, 7(1), p.e30018.
    OpenUrlCrossRefPubMed
  32. Dia, N., Sarr, F.D., Thiam, D., Sarr, T.F., Espié, E., OmarBa, I., Coly, M., Niang, M. and Richard, V., 2014. Influenza-like illnesses in Senegal: not only focus on influenza viruses. PLoS One, 9(3), p.e93227.
    OpenUrlCrossRefPubMed
  33. Douglas Jr, R.G., Cate, T.R., Gerone, P.J. and Couch, R.B., 1966. Quantitative rhinovirus shedding patterns in volunteers. American Review of Respiratory Disease, 94(2), pp.159–167.
    OpenUrlPubMedWeb of Science
  34. ↵
    Dietz, Klaus. “The estimation of the basic reproduction number for infectious diseases.” Statistical methods in medical research 2.1 (1993): 23–41.
    OpenUrlCrossRefPubMed
  35. Douglas, RG, Rossen, RD, Butler, WT, Couch, RB, 1967. Rhinovirus neutralizing antibody in tears, parotid saliva, nasal secretions and serum. The Journal of Immunology, 99(2), 297–303.
    OpenUrl
  36. Drăgănescu, A., Săndulescu, O., Florea, D., Vlaicu, O., Streinu-Cercel, A., Oţelea, D., Aramă, V., Luminos, M.L., Streinu-Cercel, A., Niţescu, M. and Ivanciuc, A., 2018. The influenza season 2016/17 in Bucharest, Romania–surveillance data and clinical characteristics of patients with influenza-like ill- ness admitted to a tertiary infectious diseases hospital. Brazilian Journal of Infectious Diseases, 22(5), pp.377–386.
    OpenUrl
  37. Drake CL, Roehrs TA, Royer H, Koshorek G, Turner RB, Roth T, 2000. Effects of an experimen- tally induced rhinovirus cold on sleep, performance, and daytime alertness. Physiology and Behavior: 71(1-2), 75–81.
    OpenUrlCrossRefPubMed
  38. Duvvuri, V.R., Granados, A., Rosenfeld, P., Bahl, J., Eshaghi, A. and Gubbay, J.B., 2015. Genetic diversity and evolutionary insights of respiratory syncytial virus A ON1 genotype: global and local transmission dynamics. Scientific reports, 5, p.14268.
    OpenUrl
  39. Falsey, A.R., Walsh, E.E. and Hayden, F.G., 2002. Rhinovirus and coronavirus infection-associated hospitalizations among older adults. The Journal of infectious diseases, 185(9), pp.1338–1341.
    OpenUrlCrossRefPubMedWeb of Science
  40. Falsey, A.R., Walsh, E.E., Esser, M.T., Shoemaker, K., Yu, L. and Griffin, M.P., 2019. Respiratory syncytial virus–associated illness in adults with advanced chronic obstructive pulmonary disease and/or congestive heart failure. Journal of medical virology, 91(1), pp.65–71.
    OpenUrl
  41. Fehr, A.R., Channappanavar, R. and Perlman, S., 2017. Middle East respiratory syndrome: emergence of a pathogenic human coronavirus. Annual review of medicine, 68, pp.387–399.
    OpenUrlCrossRefPubMed
  42. Feikin, D.R., Moroney, J.F., Talkington, D.F., Thacker, W.L., Code, J.E., Schwartz, L.A., Erdman, D.D., Butler, J.C. and Cetron, M.S., 1999. An outbreak of acute respiratory disease caused by Mycoplasma pneumoniae and adenovirus at a federal service training academy: new implications from an old scenario. Clinical infectious diseases, pp.1545–1550.
  43. Fica, A., Dabanch, J., Andrade, W., Bustos, P., Carvajal, I., Ceroni, C., Triantalo, V., Castro, M. and Fasce, R., 2015. Clinical relevance of rhinovirus infections among adult hospitalized patients. Brazilian Journal of Infectious Diseases, 19(2), pp.118–124.
    OpenUrl
  44. Fowlkes, A., Giorgi, A., Erdman, D., Temte, J., Goodin, K., Di Lonardo, S., Sun, Y., Martin, K., Feist, M., Linz, R. and Boulton, R., 2013. Viruses associated with acute respiratory infections and influenza-like illness among outpatients from the Influenza Incidence Surveillance Project, 2010–2011. The Journal of infectious diseases, 209(11), pp.1715–1725.
    OpenUrl
  45. Freymuth, F., Vabret, A., Rozenberg, F., Dina, J., Petitjean, J., Gouarin, S., Legrand, L., Corbet, S., Brouard, J. and Lebon, P., 2005. Replication of respiratory viruses, particularly influenza virus, rhinovirus, and coronavirus in HuH7 hepatocarcinoma cell line. Journal of medical virology, 77(2), pp.295–301.
    OpenUrlCrossRefPubMedWeb of Science
  46. Fritz, R.S., Hayden, F.G., Calfee, D.P., Cass, L.M., Peng, A.W., Alvord, W.G., Strober, W. and Straus, S.E., 1999. Nasal cytokine and chemokine responses in experimental influenza A virus infection: results of a placebo-controlled trial of intravenous zanamivir treatment. The Journal of infectious diseases, 180(3), pp.586–593.
    OpenUrlCrossRefPubMedWeb of Science
    1. P. R. Murray,
    2. E. J. Baron,
    3. J. Jorgensen,
    4. M. Pfaller M. L. Landry
    Gadsby, N. J. and Templeton, K. E. Coronaviruses. In P. R. Murray, E. J. Baron, J. Jorgensen, M. Pfaller M. L. Landry (Eds.), Manual of Clinical Microbiology (9th ed., pp. pp1414) ASM Press.
  48. ↵
    Galindo-Fraga, A., Ortiz-Hernández, A.A., Ramírez-Venegas, A., Vázquez, R.V., Moreno-Espinosa, S., Llamosas-Gallardo, B., Pérez-Patrigeon, S., Salinger, M., Freimanis, L., Huang, C.Y. and Gu, W., 2013. Clinical characteristics and outcomes of influenza and other influenza-like illnesses in Mexico City. In-ternational Journal of Infectious Diseases, 17(7), pp.e510–e517.
    OpenUrl
  49. Gerber, S.I., Erdman, D.D., Pur, S.L., Diaz, P.S., Segreti, J., Kajon, A.E., Belkengren, R.P. and Jones, R.C., 2001. Outbreak of adenovirus genome type 7d2 infection in a pediatric chronic-care facility and tertiary-care hospital. Clinical infectious diseases, 32(5), pp.694–700.
    OpenUrlCrossRefPubMedWeb of Science
  50. Graat, J.M., Schouten, E.G., Heijnen, M.L.A., Kok, F.J., Pallast, E.G., de Greeff, S.C. and Dorigo-Zetsma, J.W., 2003. A prospective, community-based study on virologic assessment among elderly people with and without symptoms of acute respiratory infection. Journal of clinical epidemiology, 56(12), pp.1218–1223.
    OpenUrlCrossRefPubMedWeb of Science
  51. Hall, C.B., Long, C.E. and Schnabel, K.C., 2001. Respiratory syncytial virus infections in previously healthy working adults. Clinical infectious diseases, 33(6), pp.792–796.
    OpenUrlCrossRefPubMedWeb of Science
  52. Harris JM, Gwaltney JM, 1996. Incubation periods of experimental rhinovirus infection and illness. Clinical Infectious Diseases: 23, 1287–90.
    OpenUrlCrossRefPubMedWeb of Science
  53. Hilleman, M.R., Gauld, R.L., Butleb, R., Stallones, R.A., Hedberg, C.L., Warfield, M.S. and Anderson, S.A., 1957. Appraisal of occurrence of adenovirus-caused respiratory illness in military populations. American journal of hygiene, 66(1), pp.29–41.
    OpenUrl
  54. Hong, J.Y., Lee, H.J., Piedra, P.A., Choi, E.H., Park, K.H., Koh, Y.Y. and Kim, W.S., 2001. Lower respiratory tract infections due to adenovirus in hospitalized Korean children: epidemiology, clinical features, and prognosis. Clinical infectious diseases, 32(10), pp.1423–1429.
    OpenUrlCrossRefPubMedWeb of Science
  55. Howard, T.S., Hoffman, L.H., Stang, P.E. and Simoes, E.A., 2000. Respiratory syncytial virus pneu- monia in the hospital setting: length of stay, charges, and mortality. The Journal of pediatrics, 137(2), pp.227–232.
    OpenUrlCrossRefPubMedWeb of Science
  56. Iwane, M.K., Edwards, K.M., Szilagyi, P.G., Walker, F.J., Griffin, M.R., Weinberg, G.A., Coulen, C., Poehling, K.A., Shone, L.P., Balter, S. and Hall, C.B., 2004. Population-based surveillance for hospi- talizations associated with respiratory syncytial virus, influenza virus, and parainfluenza viruses among young children. Pediatrics, 113(6), pp.1758–1764.
    OpenUrlAbstract/FREE Full Text
  57. Iwane, M.K., Prill, M.M., Lu, X., Miller, E.K., Edwards, K.M., Hall, C.B., Griffin, M.R., Staat, M.A., Anderson, L.J., Williams, J.V. and Weinberg, G.A., 2011. Human rhinovirus species associated with hos- pitalizations for acute respiratory illness in young US children. Journal of Infectious Diseases, 204(11), pp.1702–1710.
    OpenUrlCrossRefPubMed
  58. Johnson KM, Chanock RM, Rifkind D, Dravetz HM, Knight V. 1961. Respiratory syncytial virus infection in adult volunteers. J.A.M.A. 176:663–677, 1961.
    OpenUrlPubMed
  59. Kaiser, L., Briones, M.S. and Hayden, F.G., 1999. Performance of virus isolation and Directigen ® Flu A to detect influenza A virus in experimental human infection. Journal of clinical virology, 14(3), pp.191–197.
    OpenUrlCrossRefPubMedWeb of Science
  60. Kaiser, L., Regamey, N., Roiha, H., Deffernez, C. and Frey, U., 2005. Human coronavirus NL63 as- sociated with lower respiratory tract symptoms in early life. The Pediatric infectious disease journal, 24(11), pp.1015–1017.
    OpenUrlCrossRefPubMedWeb of Science
  61. Kessaram, T., Stanley, J. and Baker, M.G., 2015. Estimating influenza-associated mortality in New Zealand from 1990 to 2008. Influenza and other respiratory viruses, 9(1), pp.14–19.
    OpenUrl
  62. Kim, H.W., Brandt, C.D., Arrobio, J.O., Murphy, B., Chanock, R.M. and Parrott, R.H., 1979. Influenza A and B virus infection in infants and young children during the years 1957–1976. American Journal of Epidemiology, 109(4), pp.464–479.
    OpenUrlPubMedWeb of Science
  63. Kim, Y., Lee, S., Chu, C., Choe, S., Hong, S. and Shin, Y., 2016. The characteristics of Middle Eastern respiratory syndrome coronavirus transmission dynamics in South Korea. Osong public health and research perspectives, 7(1), pp.49–55.
    OpenUrl
  64. Ko, J.H., Woo, H.T., Oh, H.S., Moon, S.M., Choi, J.Y., Lim, J.U., Kim, D., Byun, J., Kwon, S.H., Kang, D. and Heo, J.Y., 2019. Ongoing outbreak of human adenovirus-associated acute respiratory illness in the Republic of Korea military, 2013 to 2018. Korean J Intern Med, 34(5), pp.1171–1171.
    OpenUrl
  65. Kondo, S. and Abe, K., 1991. The effects of influenza virus infection on FEV1 in asthmatic children: the time-course study. Chest, 100(5), pp.1235–1238.
    OpenUrlCrossRefPubMedWeb of Science
  66. Laguna-Torres, V.A., Gómez, J., Ocanã, V., Aguilar, P., Saldarriaga, T., Chavez, E., Perez, J., Zamalloa, H., Forshey, B., Paz, I. and Gomez, E., 2009. Influenza-like illness sentinel surveillance in Peru. PloS one, 4(7), p.e6118.
    OpenUrlCrossRefPubMed
    1. P. R. Murray,
    2. E. J. Baron,
    3. J. Jorgensen,
    4. M. Pfaller M. L. Landry
    Landry, Marie Louise. Rhinoviruses. In P. R. Murray, E. J. Baron, J. Jorgensen, M. Pfaller M. L. Landry (Eds.), Manual of Clinical Microbiology (9th ed., pp. 1405) ASM Press.
  68. Larranãga, C., Martínez, J., Palomino, A., Penã, M. and Carrión, F., 2007. Molecular characteriza- tion of hospital-acquired adenovirus infantile respiratory infection in Chile using species-specific PCR assays. Journal of clinical virology, 39(3), pp.175–181.
    OpenUrlCrossRefPubMed
  69. Lee, N., Qureshi, S.T., Other viral pneumonias. Crit Care Clin 29 (2013) 1045–1068.
    OpenUrlCrossRefPubMed
  70. Lee, W.M., Lemanske Jr, R.F., Evans, M.D., Vang, F., Pappas, T., Gangnon, R., Jackson, D.J. and Gern, J.E., 2012. Human rhinovirus species and season of infection determine illness severity. American journal of respiratory and critical care medicine, 186(9), pp.886–891.
    OpenUrlCrossRefPubMedWeb of Science
  71. Lessler, J., Reich, N.G., Brookmeyer, R., Perl, T.M., Nelson, K.E. and Cummings, D.A., 2009. Incubation periods of acute respiratory viral infections: a systematic review. The Lancet infectious diseases, 9(5), pp.291–300.
    OpenUrlCrossRefPubMedWeb of Science
  72. Leung, G.M., Chung, P.H., Tsang, T., Lim, W., Chan, S.K., Chau, P., Donnelly, C.A., Ghani, A.C., Fraser, C., Riley, S. and Ferguson, N.M., 2004. SARS-CoV antibody prevalence in all Hong Kong patient contacts. Emerging infectious diseases, 10(9), p.1653.
    OpenUrlCrossRefPubMedWeb of Science
  73. Levy, N., Iv, M. and Yom-Tov, E., 2018. Modeling influenza-like illnesses through composite compartmental models. Physica A: Statistical Mechanics and its Applications, 494, pp.288–293.
    OpenUrl
  74. Lipsitch, M., Cohen, T., Cooper, B., Robins, J.M., Ma, S., James, L., Gopalakrishna, G., Chew, S.K., Tan, C.C., Samore, M.H. and Fisman, D., 2003. Transmission dynamics and control of severe acute respiratory syndrome. Science, 300(5627), pp.1966–1970
    OpenUrlAbstract/FREE Full Text
  75. Louie, J.K., Hacker, J.K., Gonzales, R., Mark, J., Maselli, J.H., Yagi, S. and Drew, W.L., 2005. Characterization of viral agents causing acute respiratory infection in a San Francisco University Medical Center Clinic during the influenza season. Clinical Infectious Diseases, 41(6), pp.822–828.
    OpenUrlCrossRefPubMedWeb of Science
  76. Mahony, J.B., Petrich, A. and Smieja, M., 2011. Molecular diagnosis of respiratory virus infections. Critical reviews in clinical laboratory sciences, 48(5-6), pp.217–249.
    OpenUrlCrossRefPubMed
  77. Majumder, M.S., Rivers, C., Lofgren, E. and Fisman, D., 2014. Estimation of MERS-coronavirus repro- ductive number and case fatality rate for the spring 2014 Saudi Arabia outbreak: insights from publicly available data. PLoS currents, 6.
  78. Mendez-Dominguez, N.I., Bobadilla-Rosado, L.O., Fajardo-Ruiz, L.S., Camara-Salazar, A. and Gomez-Carro, S., 2019. Influenza in Yucatan in 2018: Chronology, characteristics and outcomes of ambulatory and hospitalized patients. Brazilian Journal of Infectious Diseases, 23(5), pp.358–362.
    OpenUrl
  79. Miller, E.K., Linder, J., Kraft, D., Johnson, M., Lu, P., Saville, B.R., Williams, J.V., Griffin, M.R. and Talbot, H.K., 2016. Hospitalizations and outpatient visits for rhinovirus-associated acute respiratory illness in adults. Journal of Allergy and Clinical Immunology, 137(3), pp.734–743.
    OpenUrl
  80. Millman, A. J., Reed, C., Kirley, P., Aragon, D., Meek, J. I., Farley, M. M …. Chaves, S. (2015). Improving Accuracy of Influenza-Associated Hospitalization Rate Estimates. Emerging Infectious Diseases, 21(9), 1595–1601. https://dx.doi.org/10.3201/eid
    OpenUrl
  81. Morrow, B.M., Hatherill, M., Smuts, H.E., Yeats, J., Pitcher, R. and Argent, A.C., 2006. Clinical course of hospitalised children infected with human metapneumovirus and respiratory syncytial virus. Journal of paediatrics and child health, 42(4), pp.174–178.
    OpenUrlCrossRefPubMed
  82. Moser, M.R., Bender, T.R., Margolis, H.S., Noble, G.R., Kendal, A.P. and Ritter, D.G., 1979. An outbreak of influenza aboard a commercial airliner. American journal of epidemiology, 110(1), pp.1–6.
    OpenUrlPubMedWeb of Science
  83. Mullooly, J.P., Bridges, C.B., Thompson, W.W., Chen, J., Weintraub, E., Jackson, L.A., Black, S., Shay, D.K. and Vaccine Safety Datalink Adult Working Group, 2007. Influenza-and RSV-associated hospitalizations among adults. Vaccine, 25(5), pp.846–855.
    OpenUrlCrossRefPubMedWeb of Science
  84. Naclerio RM, Proud D, Lichtenstein LM, Kagey-Sobotka A, Hendley JO,, Sorrentino J, Gwaltney JM, 1987. Kinins are generated during experimental rhinovirus colds. Th Journal of Infectious Diseases: 157(1), 133–142.
    OpenUrl
  85. Nandi, T., Khanna, M., Pati, D.R., Kumar, B. and Singh, V., 2018. Epidemiological surveillance and comparative analysis of patients with influenza like illness and other respiratory viruses. International Journal of Infectious Diseases, 73, p.203.
    OpenUrl
  86. ↵
    Nguyen, D.N.T., Bryant, J.E., Hang, N.L.K., Nadjm, B., Thai, P.Q., Duong, T.N., Anh, D.D., Horby, P., van Doorn, H.R., Wertheim, H.F. and Fox, A., 2016. Epidemiology and etiology of influenza-like-illness in households in Vietnam; it’s not all about the kids!. Journal of Clinical Virology, 82, pp.126–132.
    OpenUrl
  87. Nicholson, K.G., Kent, J., Hammersley, V. and Cancio, E., 1996. Risk factors for lower respiratory complications of rhinovirus infections in elderly people living in the community: prospective cohort study. Bmj, 313(7065), pp.1119–1123.
    OpenUrlAbstract/FREE Full Text
  88. Oner, A.F., Bay, A., Arslan, S., Akdeniz, H., Sahin, H.A., Cesur, Y., Epcacan, S., Yilmaz, N., Deger, I., Kizilyildiz, B. and Karsen, H., 2006. Avian influenza A (H5N1) infection in eastern Turkey in 2006. New England Journal of Medicine, 355(21), pp.2179–2185.
    OpenUrlCrossRefPubMedWeb of Science
  89. ↵
    Osthus, D. and Moran, K. R., Multiscale influenza forecasting, 2019. arxiv:1909.13766v1 [stat.AP] 30 Sep 2019.
  90. Peled, N., Nakar, C., Huberman, H., Scherf, E., Samra, Z., Finkelstein, Y., Hoffer, V. and Garty, B.Z., 2004. Adenovirus infection in hospitalized immunocompetent children. Clinical pediatrics, 43(3), pp.223–229.
    OpenUrlCrossRefPubMed
  91. Pitzer, V.E., Viboud, C., Alonso, W.J., Wilcox, T., Metcalf, C.J., Steiner, C.A., Haynes, A.K. and Grenfell, B.T., 2015. Environmental drivers of the spatiotemporal dynamics of respiratory syncytial virus in the United States. PLoS pathogens, 11(1), p.e1004591.
    OpenUrlCrossRefPubMed
  92. Pringle, C.R., Filipiuk, A.H., Robinson, B.S., Watt, P.J., Higgins, P. and Tyrrell, D.A.J., 1993. Immunogenicity and pathogenicity of a triple temperature-sensitive modified respiratory syncytial virus in adult volunteers. Vaccine, 11(4), pp.473–478.
    OpenUrlCrossRefPubMed
  93. Quandelacy, T.M., Viboud, C., Charu, V., Lipsitch, M. and Goldstein, E., 2013. Age-and sex-related risk factors for influenza-associated mortality in the United States between 1997–2007. American journal of epidemiology, 179(2), pp.156–167.
    OpenUrl
  94. Ramadan, N. and Shaib, H. (2019) ‘Middle East respiratory syndrome coronavirus (MERS-CoV): A review’, Germs, 9(1), pp. 35–42.
    OpenUrlCrossRef
  95. Reich NG, Perl TM, Cummings DAT, Lessler J, 2011. Visualizing clinical evidence: citation networks for the incubation periods of respiratory viral infections. PLoS One 6(4), 1–6.
    OpenUrlCrossRefPubMed
  96. Reina, J., López-Causapé, C., Rojo-Molinero, E. and Rubio, R., 2014. Clinico-epidemiological charac- teristics of acute respiratory infections by coronavirus OC43, NL63 and 229E. Revista Clínica Española (English Edition), 214(9), pp.499–504.
    OpenUrl
  97. Reis J., Shaman, J., 2016. RetrospectiveParameterEstimationand Forecastof RespiratorySyncytialVirusin the UnitedStates.PLoSComputBiol 12(10):e1005133. doi:10.1371/journal.pcbi.1005133
    OpenUrlCrossRefPubMed
  98. Reis, J. and Shaman, J., 2018. Simulation of four respiratory viruses and inference of epidemiological parameters. Infectious Disease Modelling, 3, pp.23–34.
    OpenUrl
  99. Riley, S., Fraser, C., Donnelly, C.A., Ghani, A.C., Abu-Raddad, L.J., Hedley, A.J., Leung, G.M., Ho, L.M., Lam, T.H., Thach, T.Q. and Chau, P., 2003. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science, 300(5627), pp.1961–1966.
    OpenUrlAbstract/FREE Full Text
    1. P. R. Murray,
    2. E. J. Baron,
    3. J. Jorgensen,
    4. M. Pfaller M. L. Landry
    Robinson, C., Echavarria, M. (2007). Adenoviruses. In P. R. Murray, E. J. Baron, J. Jorgensen, M. Pfaller M. L. Landry (Eds.), Manual of Clinical Microbiology (9th ed., pp. 1589) ASM Press.
  101. Sansone, M., Wiman, Å., Karlberg, M.L., Brytting, M., Bohlin, L., Andersson, L.M., Westin, J. and Nordén, R., 2019. Molecular characterization of a nosocomial outbreak of influenza B virus in an acute care hospital setting. Journal of Hospital Infection, 101(1), pp.30–37.
    OpenUrlCrossRef
  102. Scully, E.J., Basnet, S., Wrangham, R.W., Muller, M.N., Otali, E., Hyeroba, D., Grindle, K.A., Pappas, T.E., Thompson, M.E., Machanda, Z. and Watters, K.E., 2018. Lethal respiratory disease associated with human rhinovirus C in wild chimpanzees, Uganda, 2013. Emerging infectious diseases, 24(2), p.267.
    OpenUrl
  103. Sendra-Gutiérrez, J.M., Martín-Rios, D., Casas, I., Sáez, P., Tovar, A. and Moreno, C., 2004. An outbreak of adenovirus type 8. Euro Surveill, 9(3), pp.27–30.
    OpenUrlPubMed
  104. Sentilhes, A.C., Choumlivong, K., Celhay, O., Sisouk, T., Phonekeo, D., Vongphrachanh, P., Brey, P. and Buchy, P., 2013. Respiratory virus infections in hospitalized children and adults in Lao PDR. Influenza and other respiratory viruses, 7(6), pp.1070–1078.
    OpenUrl
  105. Shay, D.K., Holman, R.C., Newman, R.D., Liu, L.L., Stout, J.W. and Anderson, L.J., 1999. Bronchiolitis-associated hospitalizations among US children, 1980-1996. Jama, 282(15), pp.1440–1446.
    OpenUrlCrossRefPubMedWeb of Science
  106. Sonthichai, C., Iamsirithaworn, S., Cummings, D.A.T., Shokekird, P., Niramitsantipong, A., Khumket, S., Chittaganpitch, M. and Lessler, J., 2011. Effectiveness of non-pharmaceutical interventions in controlling an influenza A outbreak in a school, Thailand, November 2007. Outbreak, surveillance and investigation reports, 4(2), pp.6–11.
    OpenUrl
  107. Tam, P.Y.I., Zhang, L. and Cohen, Z., 2018. Clinical characteristics and outcomes of human rhinovirus positivity in hospitalized children. Annals of thoracic medicine, 13(4), p.230.
    OpenUrl
  108. Tanz, R.R. “Sore Throat”, Kliegman, R.M., Lye, P.S., Bordini, B.J., Toth, H. and Basel, D., 2017. Nelson Pediatric Symptom-Based Diagnosis E-Book. Elsevier Health Sciences.
  109. ↵
    Taylor, S., Lopez, P., Weckx, L., Borja-Tabora, C., Ulloa-Gutierrez, R., Lazcano-Ponce, E., Kerdpanich, A., Weber, M.A.R., de Los Santos, A.M., Tinoco, J.C. and Safadi, M.A.P., 2017. Respiratory viruses and influenza-like illness: epidemiology and outcomes in children aged 6 months to 10 years in a multicountry population sample. Journal of Infection, 74(1), pp.29–41.
    OpenUrl
  110. Tsolia, M.N., Kafetzis, D., Danelatou, K., Astra, H., Kallergi, K., Spyridis, P. and Karpathios, T.E., 2003. Epidemiology of respiratory syncytial virus bronchiolitis in hospitalized infants in Greece. European journal of epidemiology, 18(1), pp.55–61.
    OpenUrlPubMedWeb of Science
  111. Tyrell, D.A.J., Cohen, S. and Schilarb, J.E., 1993. Signs and symptoms in common colds. Epidemiology Infection, 111(1), pp.143–156.
    OpenUrlPubMed
  112. Valtonen, M., Waris, M., Vuorinen, T., Eerola, E., Hakanen, A.J., Mjosund, K., Grönroos, W., Heinonen, O.J. and Ruuskanen, O., 2019. Common cold in Team Finland during 2018 Winter Olympic Games (PyeongChang): epidemiology, diagnosis including molecular point-of-care testing (POCT) and treat- ment. British journal of sports medicine, 53(17), pp.1093–1098.
    OpenUrlAbstract/FREE Full Text
  113. ↵
    Van Asten, L., van den Wijngaard, C., van Pelt, W., van de Kassteele, J., Meijer, A., van der Hoek, W., Kretzschmar, M. and Koopmans, M., 2012. Mortality attributable to 9 common infections: significant effect of influenza A, respiratory syncytial virus, influenza B, norovirus, and parainfluenza in elderly persons. The Journal of infectious diseases, 206(5), pp.628–639.
    OpenUrlCrossRefPubMed
  114. Van Beek, J., Veenhoven, R.H., Bruin, J.P., Van Boxtel, R.A., de Lange, M.M., Meijer, A., Sanders, E.A., Rots, N.Y. and Luytjes, W., 2017. Influenza-like illness incidence is not reduced by influenza vaccination in a cohort of older adults, despite effectively reducing laboratory-confirmed influenza virus infections. The Journal of infectious diseases, 216(4), pp.415–424.
    OpenUrlCrossRefPubMed
  115. ↵
    Van den Driessche, P. and Watmough, J., 2002. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical biosciences, 180(1-2), pp.29–48.
    OpenUrlCrossRefPubMedWeb of Science
  116. Van Gageldonk-Lafeber, A.B., Heijnen, M.L.A., Bartelds, A.I., Peters, M.F., van der Plas, S.M. and Wilbrink, B., 2005. A case-control study of acute respiratory tract infection in general practice patients in The Netherlands. Clinical Infectious Diseases, 41(4), pp.490–497.
    OpenUrlCrossRefPubMedWeb of Science
  117. Varghese, B.M., Dent, E., Chilver, M., Cameron, S. and Stocks, N.P., 2018. Epidemiology of viral respiratory infections in Australian working-age adults (20–64 years): 2010–2013. Epidemiology Infec- tion, 146(5), pp.619–626.
    OpenUrl
  118. Velasco-Hernández, J.X., Núñez-López, M., Comas-García, A., Cherpitel, D.E.N. and Ocampo, M.C., 2015. Superinfection between influenza and RSV alternating patterns in San Luis potosí state, México. PloS one, 10(3), p.e0115674.
    OpenUrl
  119. Virlogeux, V., Park, M., Wu, J.T. and Cowling, B.J., 2016. Association between severity of MERS-CoV infection and incubation period. Emerging infectious diseases, 22(3), p.526.
    OpenUrl
  120. Wallinga, J. and Lipsitch, M., 2006. How generation intervals shape the relationship between growth rates and reproductive numbers. Proceedings of the Royal Society B: Biological Sciences, 274(1609), pp.599–604.
    OpenUrlCrossRef
  121. Wat, D., 2004. The common cold: a review of the literature. European Journal of Internal Medicine, 15(2), pp.79–88.
    OpenUrl
  122. Weber, A., Weber, M. and Milligan, P., 2001. Modeling epidemics caused by respiratory syncytial virus (RSV). Mathematical biosciences, 172(2), pp.95–113.
    OpenUrlCrossRefPubMed
  123. Welliver Sr, R.C., Checchia, P.A., Bauman, J.H., Fernandes, A.W., Mahadevia, P.J. and Hall, C.B., 2010. Fatality rates in published reports of RSV hospitalizations among high-risk and otherwise healthy children. Current medical research and opinion, 26(9), pp.2175–2181.
    OpenUrlCrossRefPubMed
  124. Wesley, A.G., Pather, M. and Tait, D., 1993. Nosocomial adenovirus infection in a paediatric respi- ratory unit. Journal of Hospital Infection, 25(3), pp.183–190.
    OpenUrlCrossRefPubMedWeb of Science
  125. ↵
    WHO, “Influenza Burden of Disease,” https://www.who.int/influenza/surveillancemonitoring/bod/en/. Accessed on 1/28/2020.
  126. WHO, “MERS Situation Update, November 2019,” accessed on January 30, 2020. http://applications.emro.who.int/docs/CSR-241-2019-EN.pdf?ua=1ua=1ua=1
  127. Zaas, A.K., Chen, M., Varkey, J., Veldman, T., Hero III, A.O., Lucas, J., Huang, Y., Turner, R., Gilbert, A., Lambkin-Williams, R. and Øien, N.C., 2009. Gene expression signatures diagnose influenza and other symptomatic respiratory viral infections in humans. Cell host & microbe, 6(3), pp.207–217.
    OpenUrlCrossRefPubMedWeb of Science
Back to top
Posted February 05, 2020.
Download PDF
Data/Code
Email
Epidemiological parameter review and comparative dynamics of influenza, respiratory syncytial virus, rhinovirus, human coronavirus, and adenovirus
Julie A. Spencer, Deborah P. Shutt, Sarah K. Moser, Hannah Clegg, Helen J. Wearing, Harshini Mukundan, Carrie A. Manore
medRxiv 2020.02.04.20020404; doi: https://doi.org/10.1101/2020.02.04.20020404
Twitter logo Facebook logo LinkedIn logo Mendeley logo
Citation Tools

Subject Area