Controlling multiple COVID-19 epidemic waves: an insight from a multi-scale model linking the behavior change dynamics to the disease transmission dynamics

2.1 Co-evolution model and model fitting

We propose a co-evolution model linking the disease transmission dynamics to the behavioral change dynamics (SI Fig.2) [18-20]. Transmission dynamics follows a compartmental scheme (SEIAHR model for COVID-19), where individuals are divided into susceptible individuals (S), exposed individuals (E), infectives with symptoms (I), asymptomatic infectives (A), hospitalized individuals (H) and recovered individuals (symptomatic recovered individuals, R_I, and asymptomatic individuals, R_A). We model the dynamics of behavioral change, which is triggered by the scare of infection of susceptible individuals, asymptomatic infected individuals and recovered individuals who did not experience symptoms. Let M(t) be an information variable (or perceived infection) governing the signal available to individuals as a function of infections (or particular confirmed cases), B(t) represent the fractions of individuals performing no behavior changes in term of perceived infections [18,19].

Note that in our modelling framework, Model (1), there are four key factors related to behavioral change dynamics: m, the sensitivity of individuals to perceived infection (a higher value of m indicating the higher sensitivity); η, the speed of raising the risk awareness; v, the persistence to maintain the risk awareness; ρ, the spread rate of the behavior changes among individuals. Further, as the behavior changed, q denotes the reduced transmission rate due to behavioral changes. Intervention measures were modeled through modifications of the diagnosis rate (continuous function), disease-induced death rate (piece-wise function of time), behavioral change-related parameters (q, η, ρ) as piece-wise functions of time accounting for the variation in interventions at different epidemic phases.

The least squares (LS) method was used to fit the proposed model and the bootstrap approach was used to obtain the 95% confidence interval (Fig. 1), and the estimated parameters and their standard deviations are listed in Table 1. In particular, the empirical distributions of the estimated key parameters for behavioral changes, (q, ρ, η,v,m), for Hongkong and the world from the bootstrap method (500 bootstrap samples), are shown in SI Fig. 3. We also obtained the estimate of the effective reproduction numbers and their confidence intervals for the three regions/countries (Hongkong, Japan, USA) and the world based on the bootstrap method (Fig. 1). The multi-scale model is proposed to capture the transmission dynamics of COVID-19 epidemics as well as the evolution of behavioral changes, and the model was calibrated based on COVID-19 epidemic data from multiple sources, and then used to evaluate the impact of enhancing/relieving NPIs upon vaccination. More details are available in the section of Methods.

• Download figure
• Open in new tab

Fig 1.

Model fitting results for Model (1): The blue curves are the estimated curves with the shadow areas as the corresponding 95% confidence band. The red cycles are the observed data of the daily reported cases and the accumulative death cases

2.2 Evolution of behavioral changes and multiple epidemic waves

Based on the model fitting results, we obtained the estimate of evolution of perceived infection (M(t)) and the dynamics of proportion of the humans with behavioral changes (1 − B(t)) for three regions/countries and the world, as shown in Fig. 2. It is worth noting that the estimated perceived infection and its corresponding behavioral changes behave oscillatively, in particular, for Japan and Hongkong, which might be the main factor to induce multiple epidemic waves in these two regions/countries. Taking Hongkong as an example, as the epidemic initially increased quickly, the individuals consciously or compulsively chose to change their behaviors to reduce the risk of being infected and the proportion of the population with behavioral changes quickly increased close to 100% around the time of the first epidemic peak. Then, the quickly changed behaviors induced the epidemic to decline swiftly and the daily reported cases reduced to almost zero. This in turn drove individuals to return back to normal behaviors, and consequently the susceptible population size rebounded back to a higher level, which induced another epidemic wave. This feedback loop, epidemic increasing → behavior changing → epidemic declining → behavior changing back → epidemic resurging, could repeat multiple times to drive multiple COVID-19 epidemic waves as observed in Hongkong or Japan (Figs. 1 and 2). From Fig. 1, we can see that the proposed model by integrating behavioral change dynamics and the disease transmission dynamics could capture the observed multiple waves of COVID-19 epidemics very well.

• Download figure
• Open in new tab

Fig. 2.

Estimated behavioral dynamics: 1 −B(t) and M (t). The solid curves are the estimated dynamic curves with the shadow areas as the corresponding 95% confidence intervals based on the bootstrap method. The black dash curves are the estimated daily reported cases from Model (1).

Note that we also observed the third epidemic wave in Japan that lasted longer and higher than the first two waves, although most people chose to change their behaviors during the third wave. Similar phenomenon was also observed in USA and the global COVID-19 epidemics (Fig. 2). Then, the interesting question is why the behavioral change did not significantly induce the epidemic to decline in the later waves. To address this question, we further examined the evolution of key parameters related to behavioral changes. The estimates of behavior-related dynamic parameters, the reduced transmission rate due to alternative behaviors (q), the response rate of perceived infection prevalence (η), and the spreading rate of behavior changes (ρ) for Japan and USA are shown in Fig. 3. We can see that the parameter q(t), the reduced transmission rate due to alternative behaviors exhibited an increasing trend during the multiple waves for USA and Japan. This suggests that the effect of behavioral changes in terms of reduction in transmission rate significantly decreased in later waves either due to waning of adherence to the NPIs or pandemic fatigue (i.e., fatigue of risk awareness of self-protection). Therefore, not only the proportion of the population, but also the effectiveness of alternative behaviors to reduce the risk of being infected is critical to prevent the epidemic from continuously surging.

• Download figure
• Open in new tab

Fig 3.

Evolution of the estimated values of the three key parameters related to behavioral changes in Japan and USA.

2.3 Effect of behavioral changes on controlling multiple COVID-19 epidemic waves

We further evaluated whether the subsequent epidemic waves could be avoided if the effectiveness of behavioral changes could be enhanced after the first wave. If the adherence of NPIs and awareness of self-protection were enhanced so that the reduced transmission rate due to the alternative behaviors (q) during the second and third waves was the same as that during the first wave, the simulated daily new cases in USA and Japan were shown in Fig. 4(A-B), from which we can see that the magnitude of second and third waves could be significantly reduced or completely avoided. This suggests that it is very important to promote and maintain the high awareness of self-protection and well adherence to the NPIs in order to avoid subsequent epidemic waves. Similarly, by controlling other behavioral change parameters, (η, ρ, m, v), it could also mitigate COVID-19 epidemics, which is demonstrated for the case of Hongkong in Fig. 4(C-F). That is, the peak magnitude of subsequent waves could be reduced by accelerating the risk awareness, spreading of behavioral changes and increasing the sensitivity of individuals to perceived infection (i.e., increasing the values of (η, ρ,m)) as well as prolonging the period of higher risk awareness (reducing the value of v).

• Download figure
• Open in new tab

Fig. 4.

Simulated daily reported cases based on Model (1) with different assumptions of behavioral dynamic parameters. (A)-(B) Daily reported cases in USA and Japan under different scenarios by decreasing the values of q in Phases 2 and 3. (C)-(F) Daily reported cases in Hongkong by varying the four parameters related to behavioral change dynamics. The subscript ‘e’ indicates the estimated value from the observed data. The values of all other parameters were set as those listed in Table 1.

2.4 Relaxation of NPIs under vaccination

The COVID-19 vaccines started to be available in some countries from December 2020. With vaccination, people’s perceived risk of infection might be changed and this may affect the behavioral changes. To investigate the evolution of behavioral changes under vaccination and the trade-off effect between relaxation of NPIs and vaccination on COVID-19 epidemics, we extended Model (1) to include the effect of vaccination, see Model (2) in sections of Methods. We re-estimated the parameters related to behavioral changes, (q, ρ, η,m,v) and other vaccination-related parameters by fitting Model (2) to the observed epidemic data (daily new cases) and daily vaccinated population data between Dec 21st, 2020 to Feb 14th, 2021 in the USA where the COVID-19 vaccination was implemented during this period. We fixed other model parameters as those in Model (1) before vaccination started. The model fitting results are shown in SI Fig. 4. The updated estimates of behavioral change-related parameters q₄, ρ ₄, η₄,m_A, and v₄ in the fourth phase (i.e., the phase with vaccination) and the estimated values of vaccination rates μ ₀,r _μ, and μ_b. are listed in Table 2. From Table 1 and Table 2, we can see that the reduced transmission rate due to alternative behaviors q is less than that in the previous two phases (i.e., q₄ < q₂ < q₃), which indicates the enhanced implementation of NPIs and/or the greater adherence to NPIs during the 4^th phase. We can also see from SI Fig. 4(C) that the vaccination coverage (received two doses of vaccines) only reached around 5% by Feb 14, 2020, which was still far from enough.

Note that the number of daily reported cases in USA has been declining since Dec 20th, 2020. To identify which factor mainly contributed to the declining trend, we did simulations for the epidemic from December 20 to June 30, 2021 using the established Model (2) by considering two scenarios of the reduced transmission rate due to alternative behaviors q: one as the estimated values for the 4^th phase and another as returning to the higher level of Phase 3, under the condition with and without vaccination (the vaccination rate μ₀ was set as the estimated values for the 4^th phase). The simulated results for the four cases are shown in Fig. 5(A), from which we can see that the epidemic curves with and without vaccination are very close to each other during the period between Dec 20th, 2020 to Feb 14th, 2021, but the difference in epidemic curves between different values of q is much bigger. This indicates that the key factor for significant decline of observed daily cases during this period is more likely due to the altered behavioral changes, instead of vaccination effect. While, as the vaccination persistently continues, it starts to play its role in mitigating the epidemic, which could be seen by a big divergence between the two epidemic curves with and without vaccination in later times.

• Download figure
• Open in new tab

Fig. 5.

Simulation and prediction results from the vaccination model (2) for USA. (A) Two scenarios of the reduced transmission rate due to alternative behaviors (q): one as the estimated values for the 4^th phase and another as returning to the higher level of Phase 3 , under the condition with vaccination (the vaccination rate p₀ was set as the estimated values for the 4^th phase, μ₀ = μ_0e) and without vaccination (μ₀ = 0). (B1)-(B2) q increased since Feb 14, 2021, where the vaccination rate was set as the estimated value from the data (B1) and no vaccination was used (B2). (C1)-(C3) q increased to 20% higher than that in Phase 3 since Feb 14, 2021 and the different vaccination rates were used. The vaccination coverage can reach around 40% till the end of June 2021 under the estimated vaccination rate from the current data, while the coverage could increase to over 60% by tripling the maximum vaccination rate μ_b. The subscript ‘e’ indicating the estimated value from the data.

It is expected that the human behaviors may be likely to change to less adherence to NPIs with widespread availability of COVID-19 vaccines, which would inevitably induce a higher level of the reduced transmission rate due to alternative behaviors (q). We performed simulations to predict the COVID-19 epidemic trend from Feb 14th to June 30^th, 2021 (Phase 5) using the established Model (2) by assuming q to increase from q₄, q₃, and 10% to 20% higher than q₃. The two cases with and without vaccination (the vaccination rate u₀ was set as the estimated value for the 4^th phase) were simulated and the results are shown in Fig. 5(B1) and (B2), respectively. The predicted results show that a higher value of q due to relaxation of NPIs could induce another big epidemic wave in USA during Phase 5 without vaccination (Fig. 5(B2)); but fortunately, continued vaccination could flatten the new wave significantly (Fig. 5(B1)). To further evaluate the effect of accelerated vaccination during Phase 5, we also simulated the scenario that the maximum vaccination rate would be tripled during Phase 5 under the worst condition of reduced transmission rate due to alternative behaviors, q = 1.2 q₃. The results are shown in Fig. 5(C1)-(C3), indicating that the accelerated vaccination could effectively flatten or even avoid the subsequent epidemic waves due to relaxation of NPIs.

Data

The COVID-19 epidemic data were obtained from the Johns Hopkins University Center for Systems Science and Engineering (JHU CCSE) and the data are available on the Github and the Humanitarian Data Exchange [28,29]. We used the data of daily COVID-19 confirmed cases and accumulative death cases in Hongkong, Japan, USA, and the world (including 273 countries or regions), as shown in SI Fig.1. We assumed that the local community transmission begun when there were continuously reported cases for 5 days. Consequently, the data collected in Hongkong, Japan, USA, and the whole world started on February 4th, 11th, 29th, and January 23rd, 2020 respectively. As we can see from the epidemic data, Hongkong, Japan and USA have already experienced multiple epidemic waves during 2020, and the last wave was much more serious with a much higher peak in Japan and USA than that of the first two waves. We obtained the data of the daily vaccinated population in USA (who received two doses) from the US Centers for Disease Control and Prevention (CDC) [30]. The data were released and analyzed anonymously [28-30].

The multi-scale dynamic models

Individuals may reduce their susceptibility or infectivity by changing behaviors in response to the growing epidemic. Reduction of contact rate or transmission probability can be achieved by taking self-protective actions such as keeping social distancing, wearing masks, and washing hands. To model the behavioral changes triggered by the scare of infection, we propose a co-evolution model linking the disease transmission dynamics to the behavioral change dynamics (SI Fig. 2).

The SEIR model is modified to an SEIAHR model for disease transmission dynamics by considering symptomatic/asymptomatic infected individuals. The total population N is divided into susceptible individuals (S), exposed individuals (E), infectives with symptoms (I), asymptomatic infectives (A), hospitalized individuals (H), recovered individuals (R_I) and asymptomatic recovered individuals (R_A). The perceived risk of infection contributes to the evolution of human behavioral changes in response to the scare of being infected. Then the perceived infection (called information index, denoted by M) or information spreading process is assumed to be related to the number of new confirmed cases and faded through an exponentially fading memory model. The dynamics of behavioral changes can be described by the imitation dynamics, which is a learning process. Expected payoffs of two different behavioral strategies (say, normal or altered behavior) are compared with each other, and individuals may change their strategy when they become aware that their payoff can be increased by adopting an alternative behavior. Let B be the fractions of population who perform no behavioral changes. Then, the model can be written as, where . Parameter 0 ≤ q ≤ 1 is the reduced transmission rate due to the altered behavior in response to the risk of infection. If q = 0, the transmission rate is reduced to 0 because of the altered behavior; if q = 1, the altered behavior does not change the transmission rate. Parameter 1/σ is the incubation period and Q is the probability of suffering symptoms after being infected. δ_I(t) is the detection rate of symptomatically infected individuals and α (t) is the disease-induced death rate. Parameters (γ_I, γ_A,γ_H) are the recovery rates of symptomatic infected, asymptomatic infected and hospitalized individuals, respectively. Parameter η is the response rate of perceived infection because of the number of newly confirmed cases, v is the decay rate of the perceived risk, and m is the sensitivity of individuals to perceived infection, where a higher value of m indicates that individuals perceive the disease as more dangerous. Parameter ρ represents the speed of the imitation process with respect to the disease transmission dynamics. The definitions and values of other parameters are given in Table 1.

Considering the continuous improvement of testing capacity, the diagnosis rate is set to be an increasing function of time t with the following form [35]: where δ_I0 is the initial diagnosis rate while δ_Im is the maximum diagnosis rate, and r is the corresponding exponential increasing rate. As reported in several studies [36,37], the COVID-19 fatality rate is varying overtime. Hence, the disease-induced death rate α is set to be a piecewise function of time t with three phases: Here, we assumed that T_dl = 150,100,80,80 (day) and T_d2 = 250,220,200,200 (day) in Hongkong, Japan, USA, and global area, respectively. Similarly, to represent the behavioral change-epidemic feedback loop for multiple waves in Japan and USA (see SI Fig.1), we chose piecewise smooth functions for behavioral dynamics-related parameters (q, ρ, η), see details in SI. Note that, although Hongkong experienced three similar epidemic waves till December, 2020, we set the behavioral dynamics-related parameters (q, ρ, η) as positive constants during the time period considered in this study. The global epidemic of COVID-19 only experienced one epidemic wave (still in the increasing phase) till Dec 20th, 2020, we then set these parameters as constants for the global epidemic.

Considering a continuous vaccination regime, we can extend Model (1) to the following system by considering vaccine effect, 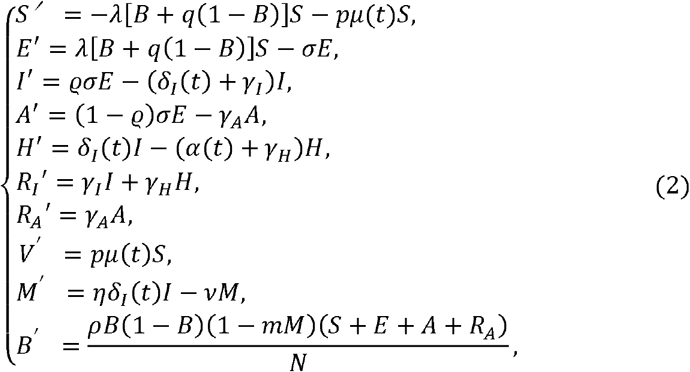where μ (t) is the time-dependent vaccination rate, as it should be small initially since the availability of the number of vaccine doses was limited at the beginning in December 2020, and then exponentially increased as the production of COVID-19 vaccines was accelerated, and finally it could be plateaued to a constant level depending on the daily vaccination capacity. Thus, we model μ (t) as a logistic increasing function of time t with the following form: where μ₀ (μ_b) is the initial (maximum) vaccination rate, r_μ is the exponential increasing rate of the vaccination. The vaccination efficacy is denoted by p with p = 95% in the USA [38,39] and the effectively vaccinated population is assumed to be immune to COVID-19 and moved to the class V (the effectively vaccinated compartment). Consequently, the time-dependent vaccination coverage can be defined as: where t₀ is the starting time of vaccination, which was set as Dec 20th, 2020 for USA.

Basic reproduction number

When all individuals are adopting the normal behavior, i.e., B=1, the basic reproduction number can be obtained as When all individuals are adopting the altered behaviors, i.e., B=0, the basic reproduction number can be derived as When considering the co-evolution of behavioral changes and the disease transmission dynamics (B ≠ 0 and B ≠ 1), the proportion of individuals adopting altered behaviors and the number of susceptible individuals are time-varying, under which we could obtain the time-varying reproduction number R(t), referring to as the effective reproduction number, This is a combination of two basic reproduction numbers.

Model fitting and parameter estimation methods

We fixed some parameters in Model (1) including the incubation period (1/σ), recovery rate of asymptomatic infections (γ_A) and symptomatic infections (γ_I), based on the existing literature as listed in Table 1. The initial total population was fixed as the whole population in the corresponding regions or countries, and the initial hospitalized and recovered populations were obtained from the database (Table 1) [28,29]. We generate 500 bootstrap samples of the time series data of daily reported cases and accumulative death cases based on a Poisson distribution (the mean of the Poisson distribution was assumed as the observed counts). We first fitted Model (1) to the 500 bootstrap samples of daily reported cases and accumulative death cases using the least squared (LS) method. We then fitted Model (2) to the 500 bootstrap samples of daily reported cases and the daily vaccinated population in USA by fixing the parameters in Model (1), except the behavior change related and vaccination related parameters. In more details, we used the least square method with a priori distribution for each parameter to fit the model to the data using the software of Matlab, where the ODE system is solved by the “ODE45” function while the “fmincon” function is used to search the optimal solutions of the objective function.