Estimating the infection and case fatality ratio for COVID-19 using age-adjusted data from the outbreak on the Diamond Princess cruise ship

Adjusting for outcome delay in CFR estimates

During an outbreak, the so-called naive CFR (nCFR), i.e. the ratio of reported deaths date to reported cases to date, will underestimate the true CFR because the outcome (recovery or death) is not known for all cases [4,5]. We can therefore estimate the true denominator for the CFR (i.e. the number of cases with known outcomes) by accounting for the delay from confirmation-to-death [5].

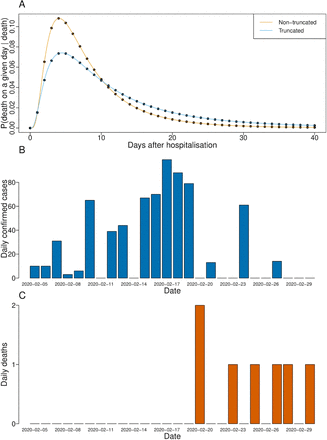
We assumed the delay from confirmation-to-death followed the same distribution as estimated hospitalisation-to-death, based on data from the COVID-19 outbreak in Wuhan, China, between the 17^th December 2019 and the 22^th January 2020, accounting right-censoring in the data as a result of as-yet-unknown disease outcomes (Figure 1, panels A and B) [6]. As a sensitivity analysis, we also consider raw “non-truncated” distributions, which do not account for censoring; the raw and truncated distributions have a mean of 8.6 days and 13 days respectively. To correct the CFR, we use the case and death incidence data to estimate the number of cases with known outcomes [5]: 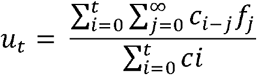where c_t is the daily case incidence at time t, f_t is the proportion of cases with delay between onset or hospitalisation and death. u_t represents the underestimation of the known outcomes [5] and is used to scale the value of the cumulative number of cases in the denominator in the calculation of the cCFR. Finally, we used the measured proportions of asymptomatic to symptomatic cases on the Diamond Princess to scale the corrected CFR (cCFR) to estimate the infection fatality ratio (IFR).

• Download figure
• Open in new tab

Figure 1:

The time-to-death distributions and case and death data used to calculate the cCFR estimates. Panel A: the delay distributions of hospitalisation-to-death; both are lognormal distributions fitted and reported in Linton et al. using data from the outbreak in Wuhan, China. The non-truncated distribution has a mean of 8.6 days and SD of 6.7 days; the right-truncated distribution has a mean of 13 days and SD of 12.7 days. Panels B and C: the case and death timeseries (respectively) of passengers onboard the ship.

Corrected IFR and CFR estimates

We estimated that the all-age cIFR on the Diamond Princess was 1.2% (0.38–2.7%) and the cCFR was 2.3% (0.75–5.3%) (Table 1). Using the age distribution of cases and deaths on the ship [2,3], we estimated that for individuals aged 70 and over, the cIFR was 9.0% (3.8–17%) and the cCFR was 18% (7.3–33%) (Table 1). The 95% confidence intervals were calculated with an exact binomial test with death count and either cases or known outcomes (depending on whether it was an interval for the naive or corrected estimate).

Using the age-stratified nCFR estimates reported in a large study in China [7], we then calculated the expected number of deaths of people who were onboard the ship in each age group, assuming this nCFR estimate was accurate. This produced a total of 15.15 expected deaths, which gives a nCFR estimate of 5% (15.15/301) for Diamond Princess (Table 2), which falls within the top end of our 95% CI. As our corrected cCFR for Diamond Princess was 2.3% (0.75% - 5.3%), this suggests we need to multiply the nCFR estimates in China [7] by a factor 46% (95% CI: 15–105%) to obtain the correct value. As the raw overall nCFR reported in the China data was 2.3% [7], this suggests the cCFR in China during that period was 1.1% (95% CI: 0.3-2.4%) and the IFR was 0.5% (95% CI: 0.2-1.2%). Based on cases and deaths reported in China up to 4th March 2020, nCFR = 2984/80422*100 = 3.71% (95% CI 3.58% - 3.84%); this naive value is significantly higher than the corrected CFR we estimate here.

The case fatality ratio is challenging to accurately estimate in real time [8], especially for an infection with attributes similar to SARS-CoV-2, which has a delay of almost two weeks between confirmation and death, strong effects of age-dependence and comorbidities on mortality risk, and likely under-reporting of cases in many settings [6]. Using an age-stratified adjustment, we accounted for changes in known outcomes over time. By applying the method to Diamond Princess data, we focus on a setting that is likely to have lower reporting error because large numbers were tested and the test has high sensitivity.

The average age onboard the ship was 58, so our estimates of cCFR cannot directly be applied to a younger population; we therefore scaled our estimates to obtain values for a population equivalent to those in the early China outbreak. There were some limitations to our analysis. Cruise ship passengers may have a different health status to the general population of their home countries, due to health requirements to embark on a multi-week holiday, or differences related to socio-economic status or comborbities. Deaths only occurred in individuals 70 years or older, so we were not able to generate age-specific cCFRs; the fatality risk may also be influenced by differences in healthcare between countries. Because of likely age-specific differences in reporting, we focused on overall cCFR in China, rather than calculating age-specific cCFRs [7].

Author contributions

TWR, AJK and WJE conceived of the study and collected the data. TWR, AJK and SA coded the methods. TWR and JH wrote the first draft of the manuscript with feedback from all other authors. KvZ, TWR, SA and CIJ worked on the statistical aspects of the study. All authors read and approved the final version of the manuscript. Each member of the CMMID COVID-19 working group contributed in processing, cleaning an interpretation of data, interpreted findings, contributed to the manuscript, and approved the work for publication.

Code Availability

All of the data and the code required to reproduce the figures and results of this study can be found at the public github repository: https://github.com/thimotei/cCFRDiamondPrincess.

Members of the Centre for the Mathematical Modelling of Infectious Diseases (CMMID) nCoV working group

The following authors were part of the Centre for Mathematical Modelling of Infectious Disease 2019-nCoV working group. Thibaut Jombart, Amy Gimma, Nikos I Bosse, Alicia Rosello, Mark Jit, James D Munday, Billy J Quilty, Petra Klepac, Hamish Gibbs, Yang Liu, Sebasitan Funk, Samuel Clifford, Fiona Sun, Kiesha Prem, Charlie Diamond, Nicholas Davies, Carl A B Pearson.

Conflict of interest

None declared.