Mathematical modeling and optimal intervention strategies of the COVID-19 outbreak

Abstract

34,354,966 active cases and 460,787 deaths because of COVID-19 pandemic were recorded on November 06, 2021, in India. To end this ongoing global COVID-19 pandemic, there is an urgent need to implement multiple population-wide policies like social distancing, testing more people and contact tracing. To predict the course of the pandemic and come up with a strategy to control it effectively, a compartmental model has been established. The following six stages of infection are taken into consideration: susceptible (S), asymptomatic infected (A), clinically ill or symptomatic infected (I), quarantine (Q), isolation (J) and recovered (R), collectively termed as SAIQJR. The qualitative behavior of the model and the stability of biologically realistic equilibrium points are investigated in terms of the basic reproduction number. We performed sensitivity analysis with respect to the basic reproduction number and obtained that the disease transmission rate has an impact in mitigating the spread of diseases. Moreover, considering the non-pharmaceutical and pharmaceutical intervention strategies as control functions, an optimal control problem is implemented to mitigate the disease fatality. To reduce the infected individuals and to minimize the cost of the controls, an objective functional has been constructed and solved with the aid of Pontryagin’s maximum principle. The implementation of optimal control strategy at the start of a pandemic tends to decrease the intensity of epidemic peaks, spreading the maximal impact of an epidemic over an extended time period. Extensive numerical simulations show that the implementation of intervention strategy has an impact in controlling the transmission dynamics of COVID-19 epidemic. Further, our numerical solutions exhibit that the combination of three controls are more influential when compared with the combination of two controls as well as single control. Therefore, the implementation of all the three control strategies may help to mitigate novel coronavirus disease transmission at this present epidemic scenario.

1 Introduction

As of November 06, 2021, the COVID-19 pandemic has already crossed 250,227,541 infected cases and more than 5,059,368 deaths throughout the world, becoming the considerable public health problem facing after the Second World War. It has a great impact to forecast the trend of SARS-CoV-2 pandemic circumstances. At this highly advanced stage, it is of utmost priority to reply some questions immediately: when the COVID-19 infection can be entirely removed by proper vaccination or immunization, and what is the interaction among the threshold of vaccination and disease reproduction number $R_0$ [1]. The SARS-CoV-2 has an important research as it was identified as pandemic by the World Health Organization (WHO) on March 11, 2020, and obtaining a lot of recognition of researchers/scientists in different areas of people knowledge.

Dynamical viewpoint is a fascinating outlook to deal with the bio-medical systems. Several literature presents different outlooks regarding dynamical models for an epidemic [2,3,4], generally utilized to delineate various infectious diseases. A fascinating and convenient outlook is relied on the population dynamics, where various individuals are employed to indicate the diseases, representing their evolution and interplays. Kermack and McKendrick [5] were one of the pioneers in developing three individuals in epidemic dynamic models, namely susceptible, infectious and recovered (SIR). Their mathematical model describes the course of epidemic exhibiting that it never be terminated necessarily by all populations becoming infectious. Anderson and May [6] modified the well-established SIR model developed by Kermack and McKendrick [5], incorporating an additional compartment: exposed class (E). Presently, most of the epidemic model is relied on the susceptible–exposed–infected–removed (SEIR) structure, widely used to delineate various infectious diseases as Hepatitis, HIV, HTLV, Dengue, Typhoid, among others.

The first case of COVID-19 was identified at Thrissur district, Kerala in India on January 30, 2020, when a student came from Wuhan, China. Due to the India COVID-19 tracker [7], there are 34,285,612 total confirmed cases, 33,661,339 recovered people and 458,470 total deaths are recorded in the Republic of India on November 06, 2021. The Govt. of India announced to maintain social distance or to adopt self-quarantine policy in order to avoid community transmission of the novel coronavirus diseases among the population. On March 22, 2020, the Indian Govt. has implemented a “Janata Curfew” during 14 h, while the total number of infected cases became more than 500 individuals. After that the Indian Govt. announced a nationwide lockdown for 21 days starting from March 25, 2020, in order to mitigate the spread of the novel coronavirus transmission. Later on, the Indian Govt. increased the nationwide lockdown to slow down the transmission of novel coronavirus pandemic. Due to the limited vaccine for COVID-19 diseases, the people must have to maintain social distance, wearing mask, avoid mass gathering or applying self-isolation to prevent the transmission of novel coronavirus [8]. The nationwide lockdown incorporates prohibition on individuals from stepping out of their houses, stop cultural functions, mass gathering, shutdown of all stores/shops excluding medicine shops, school/colleges, banks, hospitals, nursing home, etc., postponement of all the academic college/university/institution (allowed work from home only), postponement of all the private and public cars and also the closure of all cultural activities, political gathering, sports, entertainments, etc. This epidemic has significantly affected the life of all the people from economically as well as health. According to the report from the World Bank and the Reserve Bank of India (RBI), after the Second World War, this is the first time when the economic growth rate of India and the World as a whole will be diminished by 1.5–2.8% due to the effect of COVID-19 outbreak. Indeed, the expansion of this novel coronavirus outbreak has disrupted the daily life of the people, economic and the health of the people. Thus, this is one of the major issues for all the people how long this situation will continue and when the COVID-19 disease will be under maintained. In order to control the novel coronavirus diseases, the scientists around the world has been trying to improve the vaccine quality such that the disease can be eliminated.

Due to the fast expansion of novel coronavirus, which lead to necessary beds in medical colleges saturating in many countries [9], virtually many countries executed some form of non-pharmaceutical interventions (NPIs) [8, 10]. The aim of these intervention strategies was mainly to “flatten the curve” indicating that a mitigation of the coronavirus outbreak could be attained through a change of behavior in the human [11]. Flaxman et al. [10] quantifies the role of different non-pharmaceutical interventions on the transmission number, $R_t$, utilizing real data from the 11 different countries of Europe that were dealing with the novel coronavirus disease during the first wave of infections. An important interpretation is that the close progression of the non-pharmaceutical intervention strategies make it hard to obtain a clear answer as to which non-pharmaceutical intervention strategy has the most impact. Also, non-pharmaceutical intervention strategy take sometime to be effective. Thus, since the real alteration of the expansion happens much later than the intervention dates, the cumulative alteration tends to become aggregated in latest possible time window. The outbreak of COVID-19 has presented unprecedented challenges for public health and disease prevention. The transmission of COVID-19 is very efficient, in which one patient could reportedly transmit the disease to 2–3.5 other patients at the early stage [12, 13].

Nowadays, we control the epidemic associated with the ability to generate meaningful data, which in turn will allow us to use same data for mathematical modeling purposes that are the best framework to deal with forthcoming scenarios [14]. Many attempts have been taken in this field to understand the dynamics of epidemiological cycle of the epidemic [12, 15,16,17]. The adjustment of the system parameters in a dynamic way, through the imposition of limits on the system in order to optimize a given function, can be implemented through the optimal control theory [18].

Different types of mathematical models have been developed and observed to study the transmission dynamics of the novel coronavirus epidemic with their dynamical behaviors [19,20,21,22,23,24,25,26,27,28,29]. Data-driven model for the COVID-19 transmission dynamics with the incorporation of distributed time delay has been investigated by Liu et al. [30]. Khyar et al. [31] proposed a multi-strain SEIR compartmental model to investigate the interactive dynamics of the novel coronavirus outbreak and showed that their model produces global dynamics. The theory of optimal control strategies has been utilized to investigate the COVID-19 disease transmission, and the authors showed that optimal doses are needed to curtail the spread of the novel coronavirus diseases [32,33,34]. Different types of qualitative behavior has been investigated in different mathematical models [35,36,37]. Data-driven modeling approach is a powerful tool to investigate the dynamics of the infectious diseases [38]. To understand the arithmetic optimization algorithm in case of COVID-19 pandemic model, reader can see the articles [39, 40]. Also, different kinds of mathematical modeling has been studied to better understand the complicated biological phenomena [41, 42].

The use of optimal control theory in infectious disease is very common: while mathematical modeling of the infectious diseases has expressed that amalgamations of hospitalization, isolation and vaccination are usually essential in order to obliterate infectious diseases, the theory of optimal control tells us how they should be managed, by giving the proper times for intervention with proper dosages [43]. This optimization technique has also been utilized in some research works within the span of novel coronavirus. The optimal control theory of a modified susceptible–exposed–infected–recovered (SEIR) mathematical model has been investigated with the goal to aim to study the effectiveness of two inflexible lockdown techniques on the United Kingdom population [44]. Another novel coronavirus case studies incorporate the utilization of the theory optimal control in the USA [45]. An optimal use of an hypothetical vaccine for novel coronavirus has been also studied [46]. Non-pharmaceutical intervention strategies can be used as a key parameter to maintain the active number of infected populations.

Here, we are interested in applying the theory of optimal control which has a tool to understand ways to curtail the progression/development of the novel coronavirus in a case study of India by designing optimal disease intervention techniques. Furthermore, we consider some significant questions that are not completely studied in the existing literature. Our model demonstrates the implementation of optimal control technique, to minimize the symptomatic infected class and hospitalized individuals where the response applicability of public health facilities is perpetuated. As the COVID-19 epidemic has exhibited, the public health concern is not only a medical problem, but also affects the country as a whole [34]. The qualitative behavior of the interactive dynamics of the novel coronavirus epidemic has also been investigated in this manuscript. We employed three control strategies to better understand the complicated dynamics of COVID-19 transmission and to mitigate transmission of COVID-19.

The organization of the article is as follows: In the next section, we describe the proposed SAIQJR model. In the same section, we describe the qualitative behavior of the proposed model incorporating positivity, boundedness, computation of basic reproduction number, normalized forward sensitivity analysis for $R_0$, existence and stability of the biologically feasible equilibrium points. We also performed the global asymptotic stability of the disease-free equilibrium points. Moreover, we implement the optimal control strategy with three different controls and solve the control problem analytically in Sect. 3. In Sect. 4, we performed extensive numerical simulations without optimal control and with the implementation of optimal control to validate our theoretical analysis. The paper ends with a through discussion from the view point of novel coronavirus pandemic.

2 The mathematical model

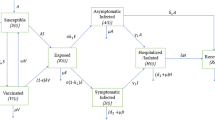
We investigate an extended SIR (susceptible–infected–recovered)-type epidemiological model that incorporates the interventions such as quarantine and hospitalization. The epidemiological model stratify the dynamics of six individuals, namely susceptible (S(t)), asymptomatic infected (A(t)), clinically ill and symptomatic infected (I(t)), quarantined (Q(t)), isolation or hospitalization (J(t)) and the recovered (R(t)). Thus, the total population N(t) is given by $N(t) = S(t) + A(t) + I(t)+ Q(t)+ J(t) + R(t)$. In our model, quarantine represents the separation of SARS-CoV-2-infected individuals from the susceptible population before the progression of the clinical symptoms, while hospitalization delineates the separation of COVID-19 infected populations with such clinical symptoms. A schematic diagram of the proposed novel coronavirus model based on the present situation of India is shown in Fig. 1. The transmission dynamics of SARS-CoV-2 is modeled by the following system of coupled nonlinear ordinary differential equations:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \Lambda _s- \beta _s(\alpha _a A + \alpha _i I + \alpha _j J)S + \beta _q Q -\delta S,\nonumber \\ \frac{\mathrm{d}A}{\mathrm{d}t}= & {} \beta _s(\alpha _a A + \alpha _i I + \alpha _j J)S - \sigma _a A -\gamma _a A -\delta A,\nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \rho _i \sigma _a A - \gamma _i I -\beta _i I -\delta I,\nonumber \\ \frac{\mathrm{d}Q}{\mathrm{d}t}= & {} (1-\rho _i) \sigma _a A - \alpha _q Q - \beta _q Q -\delta Q,\nonumber \\ \frac{\mathrm{d}J}{\mathrm{d}t}= & {} \beta _i I + \alpha _q Q - \gamma _j J -\delta J,\nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \gamma _a A+ \gamma _i I+ \gamma _j J -\delta R, \end{aligned}$$

(1)

subject to nonnegative initial conditions:

$$\begin{aligned} S(0)= & {} S^{0} \ge 0,~~~A(0)~=~ A^{0} \ge 0,~~~I(0) ~=~ I^{0} \ge 0,\nonumber \\ Q(0)= & {} Q^{0} \ge 0,~~~J(0) ~=~ J^{0} \ge 0,~~~ R(0) ~=~ R^{0} \ge 0.\nonumber \\ \end{aligned}$$

(2)

In our model, we include the demographic effects by assuming a proportional natural death rate $\delta > 0$ in each of the six individuals. Furthermore, we include the net inflow of susceptible population at the rate $\Lambda _s$ per unit time. This parameter indicates the new births and immigration of the individuals. The susceptible individuals become asymptomatic infected individuals, due to effective contact with exposed class at a rate $\beta _s$. The transmission coefficients for the asymptomatic infected, symptomatic infected and hospitalized or isolated infected populations are $\alpha _a$, $\alpha _i$, and $\alpha _j$ respectively. Among the quarantined individuals, $\alpha _q Q$ portions move to the isolation or hospitalization due to seriousness of the diseases, and the $\beta _q Q$ part become susceptible to the novel coronavirus diseases after the quarantined period. Here, $\sigma _a$ represents the rate at which asymptomatic infected individuals become clinically ill or infectious, $\rho _i$ is the rate at which asymptomatic infected individuals become symptomatic infected individuals by a proportion of $\rho _i$, and another portion $(1-\rho _i)$ move to the quarantined individuals. The term $\delta$ delineates the natural decay rate of all the individuals, whereas $\beta _i$, and $\alpha _q$ denotes the symptomatically infected individuals move to the isolated class, and quarantined individuals also move to the isolated class, respectively. The terms $\gamma _a$, $\gamma _i$, and $\gamma _j$ describe the rates at which asymptomatic infected individuals, clinically ill or symptomatic infected populations, and isolated infected individuals move to the recovered stages, respectively. Our epidemiological model is a system of coupled nonlinear ordinary differential equations. In exercise, some of the parameters may alter in time as control measures are executed or altered. The analytical calculations are studied for the model with constant parameters, and all the parameters are assumed to be positive.

Fig. 1

Schematic diagram of the novel coronavirus model (1). The epidemiological model includes six sub-populations: susceptible S, asymptomatic infected A, symptomatic infected I, quarantined Q, isolated or hospitalized J and recovered R individuals

2.1 Positivity and boundedness

The system of equations (1) is related to novel coronavirus, thus we must have to check whether the state variables are nonnegative for all time t with given initial values (2). Next, we shall investigate the solutions of the system (1) are uniformly bounded. In this purpose, we study the following theorem.

Theorem 1

All the solutions $(S(t), A(t), I(t), Q(t), J(t), R(t)) \in {{\mathbf {R}}_{+}^{6}}$ of the system (1) with initial conditions (2) remain nonnegative and are uniformly bounded in the positively invariant region $\Omega$ for all time $t \ge 0$.

Proof

Let us consider $(S(t), A(t), I(t), Q(t), J(t), R(t)) \in {{\mathbf {R}}_{+}^{6}}$ be a solution of (1) for $t \in [0, t_0)$, where $t_0 > 0$. Now, we assume that there exists some time $t_1 > 0$ such that $S(t_1) = 0$ and for the first time $t_1$, ${\mathrm{d} S(t_1)}/{\mathrm{d}t} \le 0$. But this assumption ends with a contradiction, since ${\mathrm{d}S(t_1)}/{\mathrm{d}t} \le 0 = \Lambda _s$ for the model system (1). Therefore, $S > 0$, for all $t \ge 0$.

From the first equation of (1), we obtain

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \Lambda _s- \beta _s[\alpha _i I + \alpha _a A + \alpha _j J]S + \beta _q Q -\delta S, \\\ge & {} \Lambda _s - \psi (t) S, \end{aligned}$$

where $\psi (t) = \beta _s[\alpha _i I + \alpha _a A + \alpha _j J] + \delta$. After integration, we get

$$\begin{aligned} S(t)= & {} S^0 \exp \Big (-\int _0^t \psi (s)\mathrm{d}s\Big ) \\&+ \Lambda _s \exp \Big (-\int _0^t \psi (s)\mathrm{d}s\Big ) \int _0^t e^{\int _0^s \psi (u) du} \mathrm{d}s > 0. \end{aligned}$$

Therefore, for all $t \in [0, t_0)$, we obtain that $S > 0$. The second equation of (1) can be written as

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}\ge & {} - ( \sigma _a + \gamma _a + \delta ) A, \end{aligned}$$

this leads to

$$\begin{aligned} A(t) \ge A^0 \exp \Big (-\int _0^t (\sigma _a + \gamma _a+\delta )\mathrm{d}s \Big ) \ge 0. \end{aligned}$$

Third equation of (1) gives

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}\ge & {} - (\gamma _i + \beta _i + \delta ) I, \end{aligned}$$

which implies that

$$\begin{aligned} I(t) \ge I^0 \exp \Big ( -\int _0^t ( \gamma _i + \beta _i + \delta )\mathrm{d}s \Big ) \ge 0. \end{aligned}$$

In the similar manner, we can write the fourth and fifth equations of (1) can be expressed as

$$\begin{aligned} \frac{\mathrm{d}Q}{\mathrm{d}t}\ge & {} - ( \alpha _q + \beta _q + \delta ) Q ~~\mathrm {and}~~\frac{\mathrm{d}J}{\mathrm{d}t} \ge - ( \gamma _j + \delta ) J. \end{aligned}$$

Then after integration, we have

$$\begin{aligned} Q(t)\ge & {} Q^0 \exp \Big (-\int _0^t (\alpha _q + \beta _q + \delta )\mathrm{d}s \Big ) \ge 0, \\ J(t)\ge & {} J^0 \exp \Big (-\int _0^t (\gamma _j + \delta )\mathrm{d}s \Big ) \ge 0. \end{aligned}$$

In the same way, the last equation of (1) can be expressed as

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}\ge & {} - \delta R, \end{aligned}$$

which gives

$$\begin{aligned} R(t) \ge R^0 \exp \Big (-\int _0^t \delta \mathrm{d}s \Big ) \ge 0. \end{aligned}$$

Therefore, the solutions $( S, A, I, Q, J, R )$ of (1) satisfying the initial conditions for all $t\in [0,t_0)$, $t_0 > 0$ remain nonnegative in the region $[ 0, t_0 )$.

Now, we prove the boundedness of the solutions (S, A, I, Q, J, R) of (1). The positivity of the solutions implies that

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t} \le \Lambda _s - \delta S. \end{aligned}$$

From the above equation, we can write that

$$\begin{aligned} \limsup _{t\rightarrow \infty } S \le \frac{ \Lambda _s }{ \delta }, \end{aligned}$$

and consequently,

$$\begin{aligned} S \le \frac{\Lambda _s}{\delta }. \end{aligned}$$

Here, we consider the total population N as $N = S + A + I + Q + J + R$. Taking derivative of (1), we have

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t} \le \Lambda _s - \delta N, \end{aligned}$$

this leads to

$$\begin{aligned} \limsup _{t\rightarrow \infty } N \le \frac{ \Lambda _s }{ \delta }. \end{aligned}$$

Thus, we obtain $N \le \Lambda _s/\delta$ and consequently $S + A + I + Q + J + R \le \Lambda _s/\delta .$

Therefore, all the solution trajectories $(S, A, I, Q, J, R)$ satisfying the initial conditions are uniformly bounded in ${{\mathbf {R}}_{+}^{6}}$ and in the region

$$\begin{aligned} \Omega:= & {} \Big \{(S, A, I, Q, J, R)\in {{\mathbf {R}}_{+}^{6}}: S \le \frac{\Lambda _s}{\delta },~S + A \nonumber \\&+ I + Q + J + R \le \frac{\Lambda _s}{\delta } \Big \}. \end{aligned}$$

(3)

Therefore, all the solutions of (1) initiating in ${{\mathbf {R}}_{+}^{6}}$ will enter into the region $\Omega$ in a finite time frame. $\square$

2.2 Basic reproduction number

The system of equations (1) has a unique disease-free equilibrium (DFE) point $E_0$ where $A = 0, I = 0, Q = 0$ and $J = 0$, that is, $E_0$ is defined by $E_0 (S^0, 0, 0, 0, 0, R^0)$ where $S^0 = \Lambda _s / \delta$ and $R^0 = 0$. Now, we determine the basic reproduction number $R_0$ of our compartmental model (1) using the next-generation matrix and the approach developed by Diekmann et al. [47], van den Driessche and Watmough [48], Khajanchi et al. [49]. To do this, we consider the matrix ${\mathcal {F}}$ and a non-singular M matrix ${\mathcal {V}}$, represents the creation of new-infection and transition part, respectively, for the equations (1). We linearized infectious subsystem at the DFE $E_0 (S^0, 0, 0, 0, 0, 0)$ as ${\dot{x}} = {\mathcal {F}} - {\mathcal {V}}$, where $x = (A, I, Q, J)$ are described by ${\mathcal {F}}, {\mathcal {V}}$ are given by

$$\begin{aligned}&{\mathcal {F}} = \left( \begin{array}{llll} \beta _s S [\alpha _a A + \alpha _i I + \alpha _j J ]\\ ~~~~~~~~~~~~~~~~~~~~~~0 \\ ~~~~~~~~~~~~~~~~~~~~~~0\\ ~~~~~~~~~~~~~~~~~~~~~~0 \end{array}\right) \\&~~\mathrm {and}~~{\mathcal {V}} = \left( \begin{array}{llll} ~~~~~~~~~~~~~~~~~~(\sigma _a + \gamma _a + \delta ) A \\ ~~~~~~-\rho _i \sigma _a A + (\gamma _i + \beta _i +\delta )I\\ -(1-\rho _i)\sigma _a A + (\alpha _q + \beta _q + \delta ) Q\\ ~~~-\beta _i I -\alpha _q Q + (\gamma _j + \delta )J \end{array}\right) . \end{aligned}$$

The Jacobian matrix of the model (1) can be calculated at the disease-free steady state $(A = I = Q = J = 0)$, and we get

$$\begin{aligned} F= & {} \left( \begin{array}{llll} \beta _s \alpha _a S^0 &{}\beta _s \alpha _i S^0 &{}0 &{}\beta _s \alpha _j S^0\\ ~~~~~0 &{}~~~~~0 &{}0 &{}~~~~~0 \\ ~~~~~0 &{}~~~~~0 &{}0 &{}~~~~~0 \\ ~~~~~0 &{}~~~~~0 &{}0 &{}~~~~~0 \end{array}\right) ~~~~~~\mathrm {and} \\ V= & {} \left( \begin{array}{llll} \sigma _a + \gamma _a + \delta &{} ~~~~~~~~~0 &{}~~~~~~~~~~0 &{}~~~~~~0 \\ ~~~-\rho _i \sigma _a &{}\gamma _i + \beta _i +\delta &{}~~~~~~~~~~0 &{}~~~~~~0 \\ -(1-\rho _i)\sigma _a &{} ~~~~~~~~~0 &{}\alpha _q + \beta _q + \delta &{}~~~~~~0 \\ ~~~~~~~0 &{}~~~~~-\beta _i &{}~~~~~-\alpha _q &{}~\gamma _j + \delta \end{array}\right) . \end{aligned}$$

Thus, we can derive the next-generation matrix $\rho (FV^{-1})$, and the basic reproduction number $R_0$ is the spectral radius of the next-generation matrix, and we have

$$\begin{aligned} R_0= & {} \rho (FV^{-1})= \frac{\beta _s \alpha _a S^0}{ ( \sigma _a + \gamma _a + \delta )} \nonumber \\&+ \frac{\beta _s \alpha _i \rho _i \sigma _a S^0 }{( \sigma _a + \gamma _a + \delta ) ( \gamma _i + \beta _i + \delta )}\nonumber \\&+ \frac{ \beta _s \beta _i \alpha _j \rho _i \sigma _a S^0 }{ ( \sigma _a + \gamma _a + \delta ) ( \gamma _i + \beta _i + \delta ) ( \gamma _j + \delta )} \nonumber \\&+ \frac{ \beta _s \alpha _j \alpha _q ( 1- \rho _i ) \sigma _a S^0 }{( \sigma _a + \gamma _a + \delta ) ( \alpha _q + \beta _q + \delta ) ( \gamma _j + \delta )}. \end{aligned}$$

(4)

The basic reproduction number $(R_0)$ is an epidemiologic measurement, and it helps us to convey predictions about transmissibility of emergent infectious disease like COVID-19.

Table 1 Sensitivity indices of the SAIQJR model parameters associated with $R_0$

2.3 Sensitivity analysis of $R_0$

In this subsection, we study the normalized forward sensitivity analysis of the system parameters associated with the basic reproduction number $R_0$ to analyze their robustness corresponding to the SAIQJR model system prediction as the initial transmission of any epidemic is associated with the reproduction number $R_0$. Forward sensitivity analysis helps to recognize the most effective parameters with respect to $R_0$. Since a little perturbation to the value of the most sensitive parameters can impose a great effect in any epidemiological system. Thus, to convey predictions about the prevalence of the diseases, persistence and reduction in the transmission of COVID-19 infection, we performed the normalized forward sensitivity analysis.

Definition 1

The normalized forward sensitivity index of any model parameter, m related with $R_0$ differentially is defined as:

$$\begin{aligned} \Upsilon _m^{R_0}:=\frac{\partial m}{\partial {R_0}} \times \frac{{R_0}}{m}. \end{aligned}$$

The normalized forward sensitivity index may be dependent on the model parameters or may be independent (constant value).

Now, we calculate the normalized forward sensitivity indices of the system parameters associated with $R_0$, and the indices are listed in Table 1.

From Table 1, it can be noticed that some of the sensitivity indices are positive and the rest are of negative. The positive or negative sign represents that the perturbation to these parameters can increase or decrease the value of $R_0$, respectively. As for example, it can be observed that the normalized forward sensitivity index of $\alpha _a$ is $\Upsilon _{\alpha _a}^{R_0} = +\ 0.6768$. This sensitivity index $\Upsilon _{\alpha _a}^{R_0}$ indicates that if the value of $\alpha _a$ would be increased by 10%, as a result the value of $R_0$ would be increased by 6.768%. Again, it is obtained that the sensitivity index of $\delta$ is given by $\Upsilon _{\delta }^{R_0} = -\ 0.92141$. The index $\Upsilon _{\delta }^{R_0}$ is indicating the fact that 10% increase to the value of $\delta$ will draw 9.2141% decrease to the value of $R_0$. From Table 1, it is found that the normalized forward sensitivity indices of the parameters $\Lambda _s$, $\beta _s$, $\alpha _a$, $\alpha _i$, $\alpha _j$, $\alpha _q$, $\beta _i$ and $\rho _i$ have positive influence on $R_0$ (that is, increase the value of $R_0$) and the rest of the indices (the parameters $\gamma _i$, $\beta _q$, $\sigma _a$, $\gamma _a$, $\gamma _j$ and $\delta$) create negative influence on $R_0$ (that is, decrease the value of $R_0$). In this scenario, we notice that the most effective parameters of the system (1) are the disease transmission rate ($\beta _s$) and the recruitment rate of susceptible individuals ($\Lambda _s$) which are inducing positive impact on $R_0$. Besides,the natural mortality rate of all the individuals ($\delta$) is also very influencing parameter imposing negative impact on $R_0$. We have to pay more attention to these three highly sensitive parameters to predict the COVID-19 disease transmission. We have shown this behavior of the parameters with reference to $R_0$ in Fig. 5.

2.4 Local stability in terms of the basic reproduction number

In this subsection, we studied the local asymptotic stability of the system (1) with respect to the state variables are A, I, Q, J, that is, the variational matrix related to these variables of the system (1) is as follows:

$$\begin{aligned} J_{B}=\left( \begin{array}{lllll} \beta _s\alpha _a S^0-(\sigma _a + \gamma _a + \delta ) &{}~~~~~~\beta _s\alpha _i S^0 &{}~~~~~~~~0 &{}\beta _s\alpha _j S^0\\ ~~~~~~~~\rho _i \sigma _a &{}-(\gamma _i + \beta _i + \delta ) &{}~~~~~~~~0 &{}~~~~~~0\\ ~~~~~(1-\rho _i) \sigma _a &{}~~~~~~~~~0 &{}-(\alpha _q + \beta _q + \delta ) &{}~~~~~~0\\ ~~~~~~~~0 &{}~~~~~~~~~\beta _i &{}~~~~~~~~\alpha _q &{}-(\gamma _j + \delta ) \end{array}\right) . \end{aligned}$$

From the above Jacobian matrix $J_B$, we assume that $\varpi$ be the eigenvalue of the matrix. Thus, the eigenvalues of the Jacobian matrix $J_B$ are the roots of the following characteristic equation

$$\begin{aligned} P(\varpi ) = \varpi ^4 + \zeta _1 \varpi ^3 + \zeta _2 \varpi ^2 + \zeta _3 \varpi + \zeta _4, \end{aligned}$$

(5)

where

$$\begin{aligned} \zeta _1= & {} \varrho _1 + \varrho _2 + \varrho _3 + \varrho _4 - \beta _s \alpha _a S^0,\\ \zeta _2= & {} \varrho _1 ( \varrho _2 + \varrho _3 + \varrho _4 ) + \varrho _2 \varrho _3 + \varrho _2 \varrho _3 + \varrho _3 \varrho _4 \\&- ( \varrho _2 + \varrho _3 + \varrho _4 )\beta _s \alpha _a S^0 - \beta _s \rho _i \sigma _a \alpha _i S^0, \\ \zeta _3= & {} \varrho _1 ( \varrho _2 \varrho _3 + \varrho _2 \varrho _3 + \varrho _3 \varrho _4 ) + \varrho _2 \varrho _3 \varrho _4 \\&+ ( \varrho _2 \varrho _3 + \varrho _2 \varrho _3 + \varrho _3 \varrho _4 )\beta _s \alpha _a S^0 \\&- ( \varrho _3 + \varrho _4 )\beta _s \rho _i \sigma _a \alpha _i S^0 - \beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \\&- \beta _s \alpha _q \alpha _j \sigma _a (1-\rho _i) S^0 ,\\ \zeta _4= & {} \varrho _1 \varrho _2 \varrho _3 \varrho _4 - \varrho _2 \varrho _3 \varrho _4 \beta _s \alpha _a S^0 - \varrho _3 \beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \\&- \varrho _2 \beta _s \alpha _q \alpha _j \sigma _a (1-\rho _i) S^0 - \varrho _3 \varrho _4 \beta _s \rho _i \sigma _a \alpha _i S^0, \end{aligned}$$

with $~~\varrho _1 =\sigma _a + \gamma _a + \delta , ~~\varrho _2 = \gamma _i + \beta _i + \delta , ~~\varrho _3 = \alpha _q + \beta _q + \delta , ~~\varrho _4 = \gamma _j + \delta$. Due to the well-known Lienard–Chipard test [50, 51], all the roots are negative or have negative real part, provided that the following conditions hold:

• (a)    $\zeta _\iota ~~>~~ 0$, $~~~\iota = 1, 2, 3, 4$;

• (b)    $\zeta _1 \zeta _2 ~~>~~ \zeta _3$.

To verify these expressions of the Lienard–Chipard test, we express the coefficients $\zeta _1$, $\zeta _2$, $\zeta _3$ and $\zeta _4$ of the above characteristic equation (5) in terms of $R_0$ and is written as:

$$\begin{aligned} \zeta _1= & {} \varrho _1 ( 1 - R_0 ) + \varrho _2 + \varrho _3 + \varrho _4 + \frac{ \beta _s \sigma _a S^0}{\varrho _2} \\&\Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ],\\ \zeta _2= & {} \varrho _1 ( \varrho _2 + \varrho _3 + \varrho _4 )( 1 - R_0 ) + \varrho _2 \varrho _3 + \varrho _2 \varrho _3\\&+ \varrho _3 \varrho _4 + \beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \Big [ \frac{1}{\varrho _2} + \frac{1}{\varrho _4} + \frac{\varrho _3}{\varrho _2 \varrho _4}\Big ]\\&+ \beta _s \alpha _q \alpha _j \sigma _a (1-\rho _i) S^0 \Big [ \frac{1}{\varrho _3} + \frac{1}{\varrho _4} + \frac{\varrho _2}{\varrho _3 \varrho _4}\Big ] \\&+ \beta _s \rho _i \sigma _a \alpha _i S^0 \Big [ \frac{\varrho _3}{\varrho _2} + \frac{\varrho _4}{\varrho _2}\Big ],\\ \zeta _3= & {} \varrho _1 ( \varrho _2 \varrho _3 + \varrho _2 \varrho _3 + \varrho _3 \varrho _4 ) ( 1 - R_0 ) + \varrho _2 \varrho _3 \varrho _4 \\&+\varrho _3\beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \Big [ \frac{1}{\varrho _2} + \frac{1}{\varrho _4}\Big ]\\&+ \varrho _2 \beta _s \alpha _q \alpha _j \sigma _a (1-\rho _i) S_0 \Big [ \frac{1}{\varrho _3} + \frac{1}{\varrho _4} \Big ] \\&+\frac{\varrho _3 \varrho _4}{\varrho _2} \beta _s \rho _i \sigma _a \alpha _i S^0,\\ \zeta _4= & {} \varrho _1 \varrho _2 \varrho _3 \varrho _4 ( 1 - R_0 ). \end{aligned}$$

Furthermore, we also calculate the expression $\zeta _1 \zeta _2 - \zeta _3$ in terms of $R_0$ as follows:

$$\begin{aligned} \zeta _1 \zeta _2 - \zeta _3= & {} \varrho _1 ( \varrho _2 + \varrho _3 + \varrho _4 )^2 (1-R_0) + \varrho _1^2 \\&( \varrho _2 + \varrho _3 +\varrho _4 ) (1-R_0)^2 + ( \varrho _3 + \varrho _4 )\\&( \varrho _2 \varrho _3 + \varrho _2^2 + \varrho _2 \varrho _4 + \varrho _3 \varrho _4 )\\&+ \Big ( \varrho _1 + \frac{\varrho _1 \varrho _3}{\varrho _2} + \frac{\varrho _1 \varrho _4}{\varrho _2}\Big ) (1-R_0)\beta _s \sigma _a S^0 \\&\Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]\\&+ \Big ( \frac{\varrho _2}{\varrho _4} + \frac{\varrho _4}{\varrho _2} + \frac{\varrho _3}{\varrho _4} + \frac{\varrho _3}{\varrho _2} \\&+ \frac{\varrho _3^2}{\varrho _2 \varrho _4}\Big ) \beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \\&+ \Big (\frac{\varrho _1 \varrho _3}{\varrho _2} + \frac{\varrho _1 \varrho _4}{\varrho _2}\Big )\\&(1-R_0) \beta _s \rho _i \sigma _a \alpha _i S^0\\&+ \frac{1}{\varrho _2}\Big ( \frac{1}{\varrho _2} + \frac{1}{\varrho _4} + \frac{\varrho _3}{ \varrho _2 \varrho _4}\Big )\\&\beta _s^2 \rho _i \sigma _a^2 \alpha _j \beta _i {S^0}^2\\&\Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]\\&+ \frac{1}{\varrho _2}\Big ( \frac{1}{\varrho _3} + \frac{1}{\varrho _4} + \frac{\varrho _2}{ \varrho _3 \varrho _4}\Big )\beta _s^2 \\&(1- \rho _i) \sigma _a^2 \alpha _q \alpha _j {S^0}^2\\&\Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]\\&+ \Big ( \frac{\varrho _3}{\varrho _2^2} + \frac{\varrho _4}{\varrho _2^2} \Big )\beta _s^2 \rho _i \sigma _a^2 \alpha _i {S^0}^2\\&\Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]\\&+\Big ( \frac{\varrho _1}{\varrho _2} + \frac{\varrho _1}{\varrho _4} + \frac{\varrho _1 \varrho _3}{\varrho _2 \varrho _4}\Big )\\&(1-R_0)\beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 + \frac{\varrho _3 \varrho _4 }{ \varrho _2}\beta _s \sigma _a S^0\\&\Big [\frac{\alpha _j \rho _i \beta _i}{\varrho _4} + \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]\\&+ \Big ( \frac{\varrho _1}{\varrho _3} + \frac{\varrho _1}{\varrho _4} + \frac{\varrho _1 \varrho _2}{\varrho _3 \varrho _4}\Big )(1-R_0)\beta _s\\&(1-\rho _i) \sigma _a \alpha _q \alpha _j S^0 + ( \varrho _2 + \varrho _3 + \varrho _4 )\\&\frac{\varrho _3 + \varrho _4}{\varrho _2}\beta _s \alpha _i \rho _i \sigma _a S^0\\&+ (\varrho _3 + \varrho _4 )\Big (\frac{1}{\varrho _3} \\&+ \frac{1}{\varrho _4} + \frac{ \varrho _2 }{\varrho _3 \varrho _4}\Big ) \beta _s (1-\rho _i) \sigma _a \alpha _q \alpha _j S^0 \\&+ 2 \beta _s \rho _i \sigma _a \alpha _j \beta _i S^0 \\&+ (\varrho _3 + \varrho _4 ) \beta _s \sigma _a S^0 \Big [\alpha _i \rho _i + \frac{\alpha _j \rho _i \beta _i}{\varrho _4} \\&+ \frac{\varrho _2 \alpha _j \alpha _q (1-\rho _i)}{ \varrho _3 \varrho _4}\Big ]. \end{aligned}$$

From the above expression, we can conclude that if $R_0 < 1$, then the Lienard–Chipard test holds successfully and thus the disease-free steady state $E_0( S^0, 0,$ 0, 0, 0, 0) is stable. For $R_0 > 1$, we obtain $\zeta _4 < 0$ due to Descartes’ rule of sign, we decide that at least one of eigenvalues is nonnegative. Hence, the model equations (1) is unstable. The result can be summarized in the following theorem.

Theorem 2

The disease-free steady state $E_0( S^0, 0, 0, 0, 0, 0)$ of (1) is locally asymptotically stable for $R_0 < 1$ and unstable for $R_0 > 1$.

2.5 Existence of endemic steady state

In this subsection, we determine the endemic steady state $E^* (S^*, A^*, I^*, Q^*, J^*, R^*)$ with their feasibility conditions, where

$$\begin{aligned} S^*= & {} \frac{1}{R_0}, ~I^* = \frac{\sigma _a \rho _i}{(\gamma _i + \beta _i + \delta )}A^*, \\~Q^*= & {} \frac{\sigma _a (1-\rho _i)}{(\alpha _q + \beta _q + \delta )}A^*,\\ J^*= & {} \Big [ \frac{\beta _i \sigma _a \rho _i}{(\gamma _i + \beta _i + \delta ) (\gamma _j + \delta )} \\&+ \frac{\alpha _q \sigma _a (1-\rho _i)}{(\alpha _q + \beta _q + \delta ) (\gamma _j + \delta )}\Big ]A^*\\ R^*= & {} \frac{1}{\delta }\Big [\gamma _a + \frac{\sigma _a \rho _i}{(\gamma _i + \beta _i + \delta )}\\&+ \frac{\beta _i \sigma _a \rho _i}{(\gamma _i + \beta _i + \delta ) (\gamma _j + \delta )} \\&+ \frac{\alpha _q \sigma _a (1-\rho _i)}{(\alpha _q + \beta _q + \delta )(\gamma _j + \delta )}\Big ]A^*,\\ A^*= & {} \frac{(\alpha _q + \beta _q + \delta )\Big [(\Lambda _s-\delta )+\delta (1- \frac{1}{R_0})\Big ]}{(\sigma _a + \gamma _a + \delta )(\alpha _q + \beta _q + \delta ) - \beta _q(1-\rho _i)\sigma _a}. \end{aligned}$$

The system (1) has a unique biologically feasible interior equilibrium point $E^*$, if the following conditions hold:

(i) $R_0 > 1$,   (ii) $S^0 > 1$,    (iii) $(\sigma _a + \gamma _a + \delta )(\alpha _q + \beta _q + \delta ) > \beta _q(1-\rho _i)\sigma _a$.

2.6 Global stability analysis of the disease-free steady state

Theorem 3

The disease-free steady state $E_0(\frac{\Lambda _s}{\delta },\ 0,\ 0,\ 0,\ 0,\ 0)$ of (1) is globally asymptotic stable if $R_0 < 1$ and unstable if $R_0 > 1$.

Proof

From the system of equations (1), it can be observed that the disease-free compartments of (1) are S, R and the infected compartments are A, I, Q and J. We can arrange the system equations (1) as follows:

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}= & {} P(X,\ Y), \\ \frac{\mathrm{d}Y}{\mathrm{d}t}= & {} G(X,\ Y), ~~\mathrm {and}~~G(X,\ 0) = 0, \end{aligned}$$

where

$$\begin{aligned} X= & {} (S,\ R)\in {\mathbf {R}}_{+}^{2}, ~~ Y = (A,\ I,\ Q,\ J) \in {\mathbf {R}}_{+}^{4} . \end{aligned}$$

Following the method developed by Castillo-Chavez [52], we shall try to investigate the global stability of the disease-free steady state $E_0 (\Lambda _s/\delta ,\ 0,\ 0,\ 0,\ 0,\ 0)$ and to compute this, the system equations (1) must have to satisfy the following two conditions:

• 1. $\frac{\mathrm{d}X}{\mathrm{d}t} = P(X,\ 0)$, $X^*$ is globally asymptotically stable.

• 2. $G(X,\ Y) = K Y- {\widehat{G}} (X,\ Y), {\widehat{G}} (X,\ Y) \ge 0$, where $K = D_Y G(X^*,\ 0)$ is the Metzler Matrix and $(X,\ Y) \in \Omega$, the biologically feasible and attracting region where all the solutions trajectories will enter into the interior of this region and will never leave it.

Therefore, the system (1) can be rewritten as

$$\begin{aligned}&P(X,\ 0) = \left( \begin{array}{cc} \Lambda _s - \delta S\\ 0\\ \end{array}\right) ,\\&K = \left( \begin{array}{cccc} -(\sigma _a + \gamma _a + \delta ) + \beta _s \alpha _a &{} \beta _s \alpha _i &{} 0 &{}\beta _s \alpha _j \\ \rho _i \sigma _a &{}-(\gamma _i + \beta _i + \delta ) &{} 0 &{} 0 \\ (1-\rho _i)\sigma _a &{} 0 &{}-(\alpha _q + \beta _q +\delta ) &{} 0 \\ 0 &{} \beta _i &{} \alpha _q &{}-(\gamma _j + \delta _j)\\ \end{array}\right) ,\\&\mathrm {and}~~~~{\widehat{G}}=\left( \begin{array}{cccc} \beta _s \alpha _a A (1 - S)+ \beta _s \alpha _i I(1 - S) + \beta _s \alpha _j J(1 - S) \\ 0 \\ 0\\ 0\\ \end{array}\right) . \end{aligned}$$

Therefore, it can be observed that for $(X,\ Y) \in \Omega$, ${\widehat{G}}(X,\ Y) \ge 0$ and also we can find that $X^* = (\Lambda _s/\delta ,\ 0)$ is globally asymptotic stable steady state of the limiting system, $\frac{\mathrm{d}X}{\mathrm{d}t} = P(X,\ 0)$. Accordingly, the two conditions are satisfied and in this way the disease-free steady state $E_0(\Lambda _s/\delta ,\ 0,\ 0,\ 0,\ 0,\ 0)$ is globally asymptotic stable, when $R_0 < 1$. $\square$

2.7 Local stability of endemic steady state

Theorem 4

The unique interior steady state $E^* (S^*, \ A^*, \ I^*, \ Q^*,$ $J^*, \ R^*)$ is locally asymptotically stable if $R_0 > 1$.

The standard linearization technique of the SAIQJR model around the unique interior equilibrium point is very laborious mathematically. Thus, we use the center manifold theory [52] to investigate the local asymptotic stability of the interior infection steady state $E^*$. To apply this method, we use the following simplification and change of variables are made at first. Let $S = \chi _1$, $A = \chi _2$, $I = \chi _3$, $Q = \chi _4$, $J = \chi _5$, $R = \chi _6$, using this following vector notation, the system (1) can be written in this following form as:

$$\begin{aligned} \frac{\mathrm{d}\chi _1}{\mathrm{d}t}= & {} \Lambda _s- \beta _s (\alpha _a \chi _2 + \alpha _i \chi _3 + \alpha _j \chi _5 ) \chi _1 \nonumber \\&+ \beta _q \chi _4 -\delta \chi _1 \equiv \Theta _1,\nonumber \\ \frac{\mathrm{d}\chi _2}{\mathrm{d}t}= & {} \beta _s(\alpha _a \chi _2 + \alpha _i \chi _3 + \alpha _j \chi _5 ) \chi _1 \nonumber \\&- (\sigma _a + \gamma _a + \delta ) \chi _2 \equiv \Theta _2,\nonumber \\ \frac{\mathrm{d}\chi _3}{\mathrm{d}t}= & {} \rho _i \sigma _a \chi _2 - (\gamma _i + \beta _i + \delta ) \chi _3 \equiv \Theta _3,\nonumber \\ \frac{\mathrm{d}\chi _4}{\mathrm{d}t}= & {} (1-\rho _i) \sigma _a \chi _2 - (\alpha _q + \beta _q + \delta ) \chi _4 \equiv \Theta _4,\nonumber \\ \frac{\mathrm{d}\chi _5}{\mathrm{d}t}= & {} \beta _i \chi _3 + \alpha _q \chi _4 - (\gamma _j + \delta ) \chi _5 \equiv \Theta _5,\nonumber \\ \frac{\mathrm{d}\chi _6}{\mathrm{d}t}= & {} \gamma _a \chi _2 + \gamma _i \chi _3 + \gamma _j \chi _5 -\delta \chi _6 \equiv \Theta _6. \end{aligned}$$

(6)

The variational matrix of (1) around the disease-free fixed point $E_0(S^0,\ 0,\ 0,\ 0,\ 0,\ 0)$ is given by

$$\begin{aligned} {\mathcal {J}}_{E_0}^* = \left( \begin{array}{cccccc} - \delta &{} 0 &{} - \beta _s \alpha _a S^0 &{} -\beta _q &{} - \beta _s \alpha _i S^0 &{} 0 \\ 0 &{} - (\varrho _1 - \beta _s \alpha _a S^0) &{} \beta _s \alpha _a S^0 &{} 0 &{} \beta _s \alpha _i S^0 &{} 0 \\ 0 &{} q_i\sigma _a &{} -\varrho _2 &{} 0 &{} 0 &{} 0 \\ 0 &{} (1-q_i)\sigma _a &{} 0 &{} -\varrho _3 &{} 0 &{} 0 \\ 0 &{} 0 &{} ~~\beta _i &{} ~~\alpha _q &{} -\varrho _4 &{} 0 \\ 0 &{} ~~\gamma _a &{} ~~\gamma _i &{} 0 &{} ~~\gamma _j &{} -\delta \\ \end{array}\right) . \end{aligned}$$

Here, we used $\varrho _1$, $\varrho _2$, $\varrho _3$, and $\varrho _4$ that are already mentioned as earlier before and $S^0 = \Lambda _s/ \delta$. Considering $\beta _s$ as the bifurcation parameter, we calculate $\beta _s$ by using $R_0 = 1$. Now, we compute $\beta _s$ as $\beta _s = \beta _s^*$ and is given by

$$\begin{aligned} \beta _s^*= & {} \frac{S^0 \ \varrho _1 \ \varrho _2 \ \varrho _3 \ \varrho _4}{ \alpha _a \varrho _2\varrho _3 \varrho _4 +\alpha _i \rho _i \sigma _a \varrho _3 \varrho _4 + \beta _i \alpha _j \rho _i \sigma _a \varrho _3 + \alpha _j \alpha _q ( 1- \rho _i ) \sigma _a \varrho _2 }, \end{aligned}$$

(7)

It is worthy in mentioning that one of the eigenvalues of the above Jacobian ${\mathcal {J}}^*_{E_0}$ is 0 (simple eigenvalue) and the other four eigenvalues are negative or have negative real parts. Therefore, apply the center manifold theorem [52] near $\beta _s^*$ and investigate the dynamics of the system (1).

We obtain the right eigenvector $w = [w_1~~w_2~~w_3~~w_4~~w_5~~w_6]^T$ and the left eigenvector $v = [v_1~~v_2~~v_3~~v_4~~v_5~~v_6]^T$ corresponding to the Jacobian ${\mathcal {J}}^*_{E_0}$. The components of the two eigenvectors w and v are given by

$$\begin{aligned} w_1= & {} -\frac{1}{\delta }\left[ \frac{\beta _s \alpha _a S^0 \rho _i \sigma _a}{\varrho _2} + \frac{\beta _q (1-\rho _i) \sigma _a}{\varrho _3}\right. \\&\left. + \frac{\beta _s \alpha _i S^0 \sigma _a( \beta _i \rho _i \varrho _3 + ( 1- \rho _i )\alpha _q \varrho _2) }{\varrho _2 \ \varrho _3 \ \varrho _4} \right] w_2,\\ w_2= & {} w_2 > 0,\ w_3= \frac{\rho _i \sigma _a}{ \varrho _2}w_2,\ w_4= \frac{( 1- \rho _i ) \sigma _a}{\varrho _3}w_2,~~\\ w_5= & {} \frac{\sigma _a( \beta _i \rho _i \varrho _3 + ( 1- \rho _i )\alpha _q \varrho _2)}{\varrho _2 \ \varrho _3 \ \varrho _4}w_2,\\ w_6= & {} \frac{1}{\delta } \left[ \gamma _a + \frac{\rho _i \sigma _a \gamma _i}{ \varrho _2} \right. \\&\left. + \frac{\sigma _a( \beta _i \rho _i \varrho _3 + ( 1- \rho _i )\alpha _q \gamma _j \varrho _2)}{\varrho _2 \ \varrho _3 \ \varrho _4} \right] w_2 \end{aligned}$$

and

$$\begin{aligned} v_1= & {} 0, \ v_2= v_2 > 0, \ v_3 = \beta _s S^0 \left[ \alpha _a + \frac{\beta _i \alpha _i}{\varrho _4} \right] v_2, \\ v_4= & {} \frac{\beta _s S^0 \alpha _q \alpha _i}{\varrho _3 \ \varrho _4}\\ v_2, v_5= & {} \frac{\beta _s S^0 \alpha _i}{\varrho _4} v_2, v_6 = 0. \end{aligned}$$

Thus, we can compute the constants a and b are as follows:

$$\begin{aligned} a= & {} \sum _{k, i, j = 1}^6 v_k w_i w_j \left[ \frac{\partial ^2 \Theta _k}{\partial \chi _i \partial \chi _j}(E_0)\right] _{\beta _s = \beta _s^*} \\ \mathrm {~and} ~~ b= & {} \sum _{k, i= 1}^6 v_k w_i \left[ \frac{\partial ^2 \Theta _k}{\partial \chi _i \partial \beta }(E_0)\right] _{\beta _s = \beta _s^*}, \end{aligned}$$

Considering the nonzero second order partial derivatives measured by replacing the value at the disease-free equilibrium point $E^*$ at $\beta _s = \beta _s^*$, we have

$$\begin{aligned}&a = 2 \beta _s^*v_2 w_1(w_2 \alpha _a + w_3 \alpha _i + w_5 \alpha _j)< 0,\\&\qquad \text {for}~~ w_1 < 0,\\&\text {and}~~b = v_2 (w_2 \alpha _a + w_3 \alpha _i + w_5 \alpha _j) > 0, \end{aligned}$$

Therefore, $a \ < \ 0$ and $b \ > \ 0$ at bifurcation parameter $\beta _s = \beta _s^*$ a transcritical bifurcation happens at $R_0 = 1$. Therefore, the unique interior fixed point $E^* (S^*, \ A^*, \ I^*, \ Q^*, \ J^*, \ R^*)$ is locally asymptotically stable if $R_0 > 1$ when $R_0$ is near to 1.

3 The optimal control problem

In this section, we employ the theory of an optimal control, which is a powerful tool for theoretical analysis corresponding to the infectious diseases. By using this mathematical tool, we have produced conditions which will point out the appropriate steps to mitigate the span of novel coronavirus infection in the human population. Our main aim is to minimize the infected individuals and the hospitalized individuals by using optimal intervention strategies [53]. We performed the theoretical analysis as well as numerical illustrations to show how these control strategies make an evident on the transmission of SARS-CoV-2 virus and to minimize the disease burden and their implementations. The definition of the parameters and assumptions lead to the model (1), which implies a coupled system of nonlinear differential equations with six state variables, that is, S(t), A(t), I(t), Q(t), J(t) and R(t). In this control problem, we have introduced three control variables $\eta _i(t)$ $(i=1,\ 2,\ 3)$ that externally control the number of isolated or hospitalized cases and clinically ill or symptomatic infected cases over a specified time frame.

3.1 Enhancing the response of susceptible individuals by modifying the isolation rate

Susceptible population begins to become aware of the diseases and their control strategies when they are given sufficient statistics and as a result the behavior of the population is changed. Due to the systematic news, the population has begun to wear masks, maintaining social distances with proper hygiene, remaining at quarantine and even following home isolation strategy. Thus, we have modified the isolation rate by introducing the control factor $(1 - \xi _1 \eta _1 (t))$ that quantifies the external attempt keep in preventing or controlling the of interplays between isolated (J) and susceptible (S) individuals. Therefore, in the term $\beta _s (\alpha _j (1 - \xi _1 \eta _1 (t)) J ) S$, the parameter $\beta _s$ represents the maximum transmission rate per isolated and per susceptible populations with $(1 - \xi _1 \eta _1 (t))$ representing the depletion in $\beta _s$ created by the outside isolation or hospitalized control; $\xi _1$ quantifies the usefulness of the control $\eta _1 (t)$ (where $\eta _1 (t) \in [0, \ 1]$). The most expected framework is $\xi _1 \eta _1 (t) \approx 1$, that is, the condition when interplays between isolated and hospitalized populations are almost “perfectly” avoided (prevented via successful isolation) decreasing the total transmission rate successfully to 0. Here, 0 describes no response and 1 describes fully response due to the given treatment. Therefore, this response intensity is explicitly associated with population’s behavioral response. We have taken into account this response intensity $\eta _1 (t)$ as a control variable. To increase the response among population via isolation or hospitalization, so that they alter their behavior and the cost will be associated as a nonlinear function of $\eta _1 (t)$. We wish to obtain the optimal response for susceptible population via isolation or hospitalization.

3.2 Better treatment strategy for infected individuals

To provide the better treatment policy to the symptomatic infected individuals not only decreases the disease prevalence but also influences its development. At the present scenario in novel coronavirus, we assume that the treatment is accessible and is given to the clinically ill population. As the accessibility of resources associated to medical treatments cannot be unbounded, thus in the model system (1), we introduce the treatment in the form $- \xi _2 \eta _2(t)I$. Here, $\xi _2$ denotes the treatment rate with intensity rate $\eta _2(t)$. There are different costs associated such as medicines, kits, diagnosis, health protocols and other associated costs when medication is given. Therefore, we assume that the treatment intensity $\eta _2(t)$ as a control variable lies between 0 and 1. The controlling attempt $\eta _2(t)$ changes the fraction of asymptotic infected cases $\xi _2 I(t)$ obtaining antivirals per unit of time.

3.3 Provided treatment to isolated individuals

In order to give the better treatment strategy against novel coronavirus to the isolated or hospitalized individuals at the very beginning of infection can lower the disease mortality. It also influences the development of the diseases. It can also be noted that the vaccine is accessible and given to the population who are admitted in the nursing home or hospitals in a limited amount. As the accessibility of resources associated with the medical treatments, financial crisis, disease diagnosis, etc., all the equipments are restricted. To keep this mind, we modified the model system (1) by introducing the treatment in the form $- \xi _3 \eta _3(t)J$. Here, $\xi _3$ denotes the treatment rate with intensity rate $\eta _3(t)$. There are different cost related to the medicines, health problem, isolation, vaccination, medical kits, etc., at the time of medication period that need to be taken into account. Thus, we consider $\eta _3(t)$ as a control variable that lying between 0 and 1, where 0 represents no response and 1 represents full response after the treatment. The controlling effort $\eta _3(t)$ changes the fraction of isolated population ($\xi _3 J(t)$) obtaining the antiviral treatment per unit of time. Let us consider that the controls attain maximum per capita effectiveness vaccination rates when the controls become 1.

The main aim of this section is to obtain the optimal treatment strategy and optimal controls through clinically ill infected population and isolated individuals with minimum cost with the aid of vaccination. Thus, the admissible set for three control variables $\eta _1(t)$, $\eta _2(t)$ and $\eta _3(t)$ is defined as follows:

$$\begin{aligned} {\mathcal {U}}= & {} \Big \{ \eta _1(t), \eta _2(t), \eta _3(t) : 0 \nonumber \\&\le \eta _1(t), \eta _2(t), \eta _3(t) \le 1,~t \in [0, T] \Big \}. \end{aligned}$$

(8)

The following optimal control problem is investigated with the above discussed control strategies along with the objective functional ${\mathcal {W}}$ to be minimized:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \Lambda _s- \beta _s ( \alpha _a A + \alpha _i I + \alpha _j (1 - \xi _1 \eta _1 (t)) J ) S \nonumber \\&+ \beta _q Q - \delta S,\nonumber \\ \frac{\mathrm{d}A}{\mathrm{d}t}= & {} \beta _s ( \alpha _a A + \alpha _i I + \alpha _j (1 - \xi _1 \eta _1(t) ) J ) S \nonumber \\&- \sigma _a A - \gamma _a A - \delta A,\nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \rho _i \sigma _a A - \gamma _i I - \beta _i I - \xi _2 \eta _2(t)I - \delta I,\nonumber \\ \frac{\mathrm{d}Q}{\mathrm{d}t}= & {} (1-\rho _i) \sigma _a A - \alpha _q Q - \beta _q Q - \delta Q,\nonumber \\ \frac{\mathrm{d}J}{\mathrm{d}t}= & {} \beta _i I + \alpha _q Q - \gamma _j J - \xi _3 \eta _3(t)J - \delta J,\nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \gamma _a A + \gamma _i I + \gamma _j J + \xi _2 \eta _2(t)I + \xi _3 \eta _3(t)J - \delta R,\nonumber \\ \end{aligned}$$

(9)

subject to minimize the objective functional

$$\begin{aligned}&{\mathcal {W}}( \eta _1(t), \eta _2(t), \eta _3(t) ) = \int ^T_0 \nonumber \\&\quad \Big [ \varphi _1 I + \varphi _2 J + \frac{ 1 }{ 2 } \Big ( \kappa _1 \eta _1^2(t) + \kappa _2 \eta _2^2(t) + \kappa _3 \eta _3^2(t) \Big ) \Big ] \mathrm{d}t,\nonumber \\ \end{aligned}$$

(10)

with the initial conditions are stated in Eq. (2). Here, the objective functional ${\mathcal {W}}$ represents the total incurred cost, that is, the sum of of the costs stated in the integrand:

$$\begin{aligned}&{\mathcal {W}}(S, A, I, Q, J, R, \eta _1(t), \eta _2(t), \eta _3(t) ) = \varphi _1 I + \varphi _2 J \\&\quad + \frac{ 1 }{ 2 } \Big ( \kappa _1 \eta _1^2(t) + \kappa _2 \eta _2^2(t) + \kappa _3 \eta _3^2(t) \Big ), \end{aligned}$$

represents the current value of the cost at any time t. All the parameters $\varphi _1$, $\varphi _2$, $\kappa _1$, $\kappa _2$, and $\kappa _3$ are nonnegative. They are used as a weight constants and balancing the units of the integrand. Also they represents the measure of the relative costs of the control functions over [0, T]. The control functions $\eta _1^*(t), \eta _2^*(t)$ and $\eta _3^*(t)$ exists in the admissible control set ${\mathcal {U}}$ that mainly minimized the objective functional ${\mathcal {W}}$.

3.4 Existence of optimal control

In this subsection, the existence of an optimal control of (9) is analyzed. Then, we employ the Pontryagin’s maximum principle [53] to characterize the optimal control. The Pontryagin’s maximum principle is being utilized to get necessary conditions for the three controls. To prove the existence of an optimal control, we utilize the following theorem which assured that the existence of the controls $\eta _1^*,$ $\eta _2^*$ and $\eta _3^*$ that minimizes the objective functional ${\mathcal {W}}$

Theorem 5

There exist optimal controls $\eta (t) = ( \eta _1^*(t), \eta _2^*(t), \eta _3^*(t))$ in ${\mathcal {U}}$ that minimizes the objective functional ${\mathcal {W}}( \eta _1(t), \eta _2(t), \eta _3(t))$ corresponding to the control system (9)–(10).

Proof

In Sect. 2, we have already proved that all the solutions of (1) are nonnegative and uniformly bounded for the given initial conditions (2). Nonnegativity of the objective functional is obvious and the nonnegativity implies the boundedness of the objective functional. Hence, minimizing the sequence of controls $\eta ^\tau (t) = ( \eta _1^\tau (t), \eta _2^\tau (t), \eta _3^\tau (t) )$ $\in$ ${\mathcal {U}}$ exists in such a way that

$$\begin{aligned} \lim _{ \tau \rightarrow \infty } {\mathcal {W}}( \eta ^\tau (t) ) = \inf _{ \eta \in {\mathcal {U}}} {\mathcal {W}}( \eta (t) ). \end{aligned}$$

Therefore, the controls belonging to ${\mathcal {U}}$ are uniformly bounded in $L^\infty$ and consequently they are uniform bounded in $L^2 ( [ 0, T ] )$. Since the space $L^2 ( [ 0, T ] )$ is reflexive [54], then there exists $\eta ^*(t) = ( \eta _1^*(t), \eta _2^*(t), \eta _3^*(t) )$ $\in$ ${\mathcal {U}}$ a subsequence in such a way that

$$\begin{aligned}&\eta _1^\tau (t) \rightharpoonup \eta _1^*(t), ~~\eta _2^\tau (t) \rightharpoonup \eta _2^*(t), ~~\eta _3^\tau (t)\\&\quad \rightharpoonup \eta _3^*(t)~~\mathrm {weakly~~ in }~L^2 ( [ 0, T ] )~~\mathrm {as}~\tau \rightarrow \infty . \end{aligned}$$

Then, it is obvious that the state sequence $z^\tau = ( S^\tau , A^\tau , I^\tau , Q^\tau , J^\tau , R^\tau )$ is uniformly bounded corresponding to $\eta ^\tau (t)$. It can be seen that the uniformly boundedness of the right-hand side of the system (1) implies the uniformly boundedness of the derivatives for $z^\tau$ and equi-continuity of the corresponding state sequence $z^\tau$. Due to the Arzel–Ascoli theorem, there exist $z^\tau = ( S^\tau , A^\tau , I^\tau , Q^\tau , J^\tau , R^\tau )$ such that on a subsequence,

$$\begin{aligned} z^\tau \rightarrow z^*~~~\mathrm { uniformly~~on }~~[0, T]. \end{aligned}$$

Next, we choose a proper subsequence passing through the limit of the system (1) and corresponding to the controls $\eta _1^*(t), \eta _2^*(t), \eta _3^*(t)$, we can achieve the state solution $z^*$. Then, the lower semi-continuity of the $L^2$—norm with respect to $L^2$ weak convergence implies that

$$\begin{aligned} \inf _{ \eta \in {\mathcal {U}}} {\mathcal {W}}( \eta (t) )= & {} \lim _{ \tau \rightarrow \infty } {\mathcal {W}}( \eta ^\tau (t) )\\\ge & {} \int ^T_0 \Big ( \varphi _1 I + \varphi _2 J \Big ) \mathrm{d}t +\, \frac{ 1 }{ 2 }\int ^T_0 \\&\times \Big ( \kappa _1 \eta _1^2(t) + \kappa _2 \eta _2^2(t) + \kappa _3 \eta _3^2(t) \Big ) \mathrm{d}t\\= & {} {\mathcal {W}}( \eta ^* (t) ). \end{aligned}$$

Therefore, $\eta ^*(t)$ is an optimal control. $\square$

3.5 Characterization of optimal control

Since the existence of the controls are established for minimizing the objective functional (10) subject to the state equations (9), then we employed Pontryagin’s maximum principle [53] to obtain necessary conditions for the optimal control problem [55, 56].

Theorem 6

There exists optimal controls $\eta ^*(t) = ( \eta _1^*(t), \eta _2^*(t), \eta _3^*(t) )$ $\in$ ${\mathcal {U}}$ and the corresponding state solutions $z^* = ( S^*, A^*, I^*, Q^*, J^*, R^* )$ of the system (9) that minimizes the objective functional ${\mathcal {W}}( \eta _1(t), \eta _2(t), \eta _3(t))$, then there exist adjoint variables $\vartheta _s$, $\vartheta _a$, $\vartheta _i$, $\vartheta _q$, $\vartheta _j$, and $\vartheta _r$ satisfying the following canonical equations:

$$\begin{aligned} \vartheta _s'= & {} -\Big [ ( \vartheta _a - \vartheta _s ) \beta _s ( \alpha _a A + \alpha _i I \nonumber \\&+ \alpha _j ( 1 - \xi _1 \eta _1(t) ) J ) - \vartheta _s \delta \Big ],\nonumber \\ \vartheta _a'= & {} -\Big [ ( \vartheta _a - \vartheta _s ) \beta _s \alpha _a S-\vartheta _a ( \sigma _a + \gamma _a + \delta ) \nonumber \\&+ \vartheta _i \rho _i \sigma _a + \vartheta _q (1-\rho _i) \sigma _a + \vartheta _r \gamma _a \Big ], \nonumber \\ \vartheta _i'= & {} -\Big [ \varphi _1 + ( \vartheta _a - \vartheta _s ) \beta _s \alpha _i S - \vartheta _i ( \gamma _i + \beta _i \nonumber \\&+ \delta + \xi _2 \eta _2(t)) + \vartheta _j \beta _i + \vartheta _r ( \gamma _i + \xi _2 \eta _2(t) ) \Big ], \nonumber \\ \vartheta _q'= & {} -\Big [ \vartheta _s \beta _q - \vartheta _q ( \alpha _q + \beta _q + \delta ) + \vartheta _j \alpha _q \Big ], \nonumber \\ \vartheta _j'= & {} -\Big [ \varphi _2 + ( \vartheta _a - \vartheta _s ) ( 1 - \xi _1 \eta _1(t) ) \beta _s \alpha _j S\nonumber \\&- \vartheta _j ( \gamma _j + \delta + \xi _3 \eta _3(t)) + \vartheta _r ( \gamma _j + \xi _3 \eta _3(t) ) \Big ],\nonumber \\ \vartheta _r'= & {} -\Big [ -\vartheta _r \delta \Big ], \end{aligned}$$

(11)

with the transversality conditions:

$$\begin{aligned}&\vartheta _s (T) = 0,~ \vartheta _a (T) = 0,~ \vartheta _i (T) = 0,~\\&\vartheta _q (T) = 0,~ \vartheta _j (T) = 0,~ , \vartheta _r (T) = 0. \end{aligned}$$

Moreover, the corresponding optimal controls $\eta ^*(t) = ( \eta _1^*(t), \eta _2^*(t), \eta _3^*(t) )$ are represented by

$$\begin{aligned} \eta _1^* (t)= & {} \min \Big \{ \max \Big \{ 0, \frac{(\vartheta _a -\vartheta _s ) \beta _s \xi _1 \alpha _j S J }{ \kappa _1 } \Big \}, 1 \Big \},\\ \eta _2^* (t)= & {} \min \Big \{ \max \Big \{ 0, \frac{(\vartheta _i -\vartheta _r ) \xi _2 I }{ \kappa _2 } \Big \}, 1 \Big \},\\ \eta _3^* (t)= & {} \min \Big \{ \max \Big \{ 0, \frac{(\vartheta _j -\vartheta _r ) \xi _3 J }{ \kappa _3 } \Big \}, 1 \Big \}. \end{aligned}$$

Proof

We investigate necessary conditions for the control functions with the aid of the Pontryagin’s maximum principle for the model system (9). In order to do this, we construct the Hamiltonian ${\mathcal {H}}$ which is defined for all $t \in [0, T]$ as follows:

$$\begin{aligned} {\mathcal {H}}= & {} \varphi _1 I + \varphi _2 J + \frac{1}{2} \Big ( \kappa _1 \eta _1^2(t) + \kappa _2 \eta _2^2(t) + \kappa _3 \eta _3^2(t) \Big )\\&+ \vartheta _s \Big [ \Lambda _s- \beta _s ( \alpha _a A + \alpha _i I + \alpha _j (1 - \xi _1 \eta _1(t) ) J ) S \\&+ \beta _q Q - \delta S \Big ]\\&+ \vartheta _a \Big [ \beta _s ( \alpha _a A + \alpha _i I + \alpha _j (1 - \xi _1 \eta _1(t) ) J ) S \\&- \sigma _a A - \gamma _a A - \delta A \Big ]\\&+ \vartheta _i \Big [ \rho _i \sigma _a A - \gamma _i I - \beta _i I - \xi _2 \eta _2(t)I - \delta I \Big ]\\&+ \vartheta _q \Big [ (1-\rho _i) \sigma _a A - \alpha _q Q - \beta _q Q - \delta Q \Big ]\\&+ \vartheta _j \Big [ \beta _i I + \alpha _q Q - \gamma _j J - \xi _3 \eta _3(t)J - \delta J \Big ]\\&+ \vartheta _r \Big [ \gamma _a A + \gamma _i I + \gamma _j J + \xi _2 \eta _2(t)I \\&+ \xi _3 \eta _3(t)J - \delta R \Big ], \end{aligned}$$

where $\vartheta _s$, $\vartheta _a$, $\vartheta _i$, $\vartheta _q$, $\vartheta _j$, and $\vartheta _r$ are the co-states or adjoint variables. With the aid of Pontryagin’s maximum principle, we obtain the minimized Hamiltonian which minimizes the objective functional ${\mathcal {W}}( \eta _1(t), \eta _2(t), \eta _3(t))$. Pontryagin’s maximum principle plays an important role in adjoining the objective functional with the state variables including co-states or adjoint variables.

Due to Pontryagin’s maximum principle, there exist co-states $\vartheta _s'$, $\vartheta _a'$, $\vartheta _i'$, $\vartheta _q'$, $\vartheta _j'$ and $\vartheta _r'$ that satisfies the following canonical expressions:

$$\begin{aligned} \vartheta _s'= & {} -\frac{ \partial {\mathcal {H}} }{ \partial S },~~\vartheta _a' = -\frac{ \partial {\mathcal {H}} }{ \partial A },~~\vartheta _i'=-\frac{\partial {\mathcal {H}} }{ \partial I},\\ ~~\vartheta _q'= & {} -\frac{ \partial {\mathcal {H}} }{ \partial Q },~~\vartheta _j' = -\frac{ \partial {\mathcal {H}} }{ \partial J },~~\vartheta _r'=-\frac{\partial {\mathcal {H}} }{ \partial R }, \end{aligned}$$

with the transversality conditions: $\vartheta _s (T) = 0,~ \vartheta _a (T) = 0,~ \vartheta _i (T) = 0,~ \vartheta _q (T) = 0,~ \vartheta _j (T) = 0,$ and $\vartheta _r (T) = 0$. Now, we get the characterization of optimal controls are given by

$$\begin{aligned} \frac{ \partial {\mathcal {H}} }{ \partial \eta _1(t)}= & {} 0,~~~~~\frac{ \partial {\mathcal {H}} }{ \partial \eta _2(t) } = 0,~~~~~\frac{ \partial {\mathcal {H}} }{ \partial \eta _3(t) } = 0 \end{aligned}$$

From $\partial {\mathcal {H}}/\partial \eta _1(t) = 0$, $\partial {\mathcal {H}}/\partial \eta _2(t) = 0$, and $\partial {\mathcal {H}}/\partial \eta _3(t) = 0$, we get

$$\begin{aligned} \eta _1(t)= & {} \frac{(\vartheta _a - \vartheta _s ) \beta _s \xi _1 \alpha _j S J }{ \kappa _1 } ~~~ \mathrm {at}~~ \eta _1(t) = \eta _1^*(t),\\ \eta _2(t)= & {} \frac{(\vartheta _i - \vartheta _r ) \xi _2 I }{ \kappa _2 } ~~~~~~~~~~~~~~ \mathrm {at}~~ \eta _2(t) = \eta _2^*(t),\\ \eta _2(t)= & {} \frac{(\vartheta _j - \vartheta _r ) \xi _3 J }{ \kappa _3 } ~~~~~~~~~~~~~~ \mathrm {at}~~ \eta _3(t) = \eta _3^*(t). \end{aligned}$$

By considering the upper and lower bounds for $\eta _1(t)$, $\eta _2(t)$, and $\eta _3(t)$, we have following the characterization of the optimal controls:

$$\begin{aligned} \eta _1^*(t)= & {} \min \Big \{ \max \Big \{ 0, \frac{ (\vartheta _a -\vartheta _s ) \beta _s \xi _1 \alpha _j S J }{ \kappa _1 } \Big \}, 1 \Big \}, \end{aligned}$$

(12)

$$\begin{aligned} \eta _2^*(t)= & {} \min \Big \{ \max \Big \{ 0, \frac{ (\vartheta _i -\vartheta _r ) \xi _2 I }{ \kappa _2 } \Big \}, 1 \Big \}, \end{aligned}$$

(13)

$$\begin{aligned} \eta _3^*(t)= & {} \min \Big \{ \max \Big \{ 0, \frac{ (\vartheta _j -\vartheta _r ) \xi _3 J }{ \kappa _3 } \Big \}, 1 \Big \}. \end{aligned}$$

(14)

It can also be noted that

$$\begin{aligned} \frac{ \partial ^2 {\mathcal {H}} }{ \partial \eta _1^2(t)}= & {} \kappa _1> 0,~~~~~\frac{ \partial ^2 {\mathcal {H}} }{ \partial \eta _2^2(t) } = \kappa _2> 0,\\~~~~~\frac{ \partial ^2 {\mathcal {H}} }{ \partial \eta _3^2(t) }= & {} \kappa _3 > 0, \end{aligned}$$

which assured that our optimal controls minimize the Hamiltonian.

Now, we derive the corresponding optimality system utilizing the optimal controls $\eta ^*(t) = ( \eta _1^*(t), \eta _2^*(t), \eta _3^*(t) )$ that has already been characterized in the above. The optimality system that minimized Hamiltonian ${\mathcal {H}}$ at $(S^*, A^*, I^*$, $Q^*$, $J^*, R^*, \eta _1^*, \eta _2^*, \eta _3^*, \vartheta _s, \vartheta _a, \vartheta _i, \vartheta _q, \vartheta _j, \vartheta _r)$ is given as follows:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} \Lambda _s- \beta _s ( \alpha _a A^* + \alpha _i I^* + \alpha _j (1 - \xi _1 \eta _1^* (t)) J^* ) S^* \nonumber \\&+ \beta _q Q^* - \delta S^*, \nonumber \\ \frac{\mathrm{d}A}{\mathrm{d}t}= & {} \beta _s ( \alpha _a A^* + \alpha _i I^* + \alpha _j (1 - \xi _1 \eta _1^*(t) ) J^* ) S^* \nonumber \\&- \sigma _a A^* - \gamma _a A^* - \delta A^*, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \rho _i \sigma _a A^* - \gamma _i I^* - \beta _i I^* - \xi _2 \eta _2^*(t)I^* - \delta I^*, \nonumber \\ \frac{\mathrm{d}Q}{\mathrm{d}t}= & {} (1-\rho _i) \sigma _a A^* - \alpha _q Q^* - \beta _q Q^* - \delta Q^*,\nonumber \\ \frac{\mathrm{d}J}{\mathrm{d}t}= & {} \beta _i I^* + \alpha _q Q^* - \gamma _j J^* - \xi _3 \eta _3^*(t)J^* - \delta J^*,\nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \gamma _a A^* + \gamma _i I^* + \gamma _j J^* + \xi _2 \eta _2^*(t)I^* + \xi _3 \eta _3^*(t)J^* \nonumber \\&- \delta R^*, \end{aligned}$$

(15)

with initial values: $S^{*}(0) \ge 0$, $A^*(0) \ge 0$, $I^*(0) \ge 0$, $Q^*(0) \ge 0$, $J^*(0) \ge 0$, $R^*(0) \ge 0$ and the corresponding co-states are

Fig. 2

Semi-relative sensitivities of the system parameters by using automatic differentiation. From the figures, it can be observed that the parameters $\beta _s$, $\alpha _a$, $\delta$, $\sigma _a$, $\rho _i$, $\gamma _a$, $\alpha _j$ are most effective with respect to the symptomatic infected individuals. The biologically realistic time window is [0, 400]

$$\begin{aligned} \vartheta _s'= & {} -\Big [ ( \vartheta _a - \vartheta _s ) \beta _s ( \alpha _a A^* + \alpha _i I^* \nonumber \\&+ \alpha _j ( 1 - \xi _1 \eta _1^*(t) ) J^* ) - \vartheta _s \delta \Big ], \nonumber \\ \vartheta _a'= & {} -\Big [ ( \vartheta _a - \vartheta _s ) \beta _s \alpha _a S^*-\vartheta _a ( \sigma _a + \gamma _a + \delta ) \nonumber \\&+ \vartheta _i \rho _i \sigma _a \vartheta _q (1-\rho _i) \sigma _a + \vartheta _r \gamma _a \Big ], \nonumber \\ \vartheta _i'= & {} -\Big [ \varphi _1 + ( \vartheta _a - \vartheta _s ) \beta _s \alpha _i S^* - \vartheta _i ( \gamma _i + \beta _i \nonumber \\&+ \delta + \xi _2 \eta _2^*(t)) + \vartheta _j \beta _i + \vartheta _r ( \gamma _i + \xi _2 \eta _2^*(t) ) \Big ], \nonumber \\ \vartheta _q'= & {} -\Big [ \vartheta _s \beta _q - \vartheta _q ( \alpha _q + \beta _q + \delta ) + \vartheta _j \alpha _q \Big ], \nonumber \\ \vartheta _j'= & {} -\Big [ \varphi _2 + ( \vartheta _a - \vartheta _s ) ( 1 - \xi _1 \eta _1^*(t) ) \beta _s \alpha _j S \nonumber \\&- \vartheta _j ( \gamma _j + \delta + \xi _3 \eta _3^*(t)) + \vartheta _r ( \gamma _j + \xi _3 \eta _3^*(t) ) \Big ],\nonumber \\ \vartheta _r'= & {} -\Big [ -\vartheta _r \delta \Big ], \end{aligned}$$

(16)

with the transversality conditions are $\vartheta _s (T) = 0*$, $\vartheta _a (T) = 0$, $\vartheta _i (T) = 0$, $\vartheta _q (T) = 0$, $\vartheta _j (T) = 0$, $\vartheta _r (T) = 0$, and the three controls $\eta _1^*$, $\eta _2^*$ and $\eta _3^*$ are the same as (12)–(14). Hence, the proof of the theorem. $\square$

Table 2 Description of system parameter values used for novel coronavirus model system (1)

4 Model calibration and data source

In this section, we validate our theoretical analysis based on the numerical solutions with real data from India. In order to do this, we estimate the most sensitive parameters for our SAIQJR model.

4.1 Sensitivity analysis

We have calibrated our novel coronavirus model (1) by using the daily confirmed new SARS-CoV-2 viruses and cumulative confirmed SARS-CoV-2 viruses for India. We have taken data for novel coronavirus diseases from World Health Organization (WHO) registered cases for the time period February 01, 2021, to May 21, 2021 [58]. Our proposed model (1) has a system of six coupled ordinary differential equations with 14 parameters, among them six key parameters have been estimated by using semi-relative sensitivity analysis [59], namely $\beta _s$, $\alpha _a$, $\delta$, $\sigma _a$, $\rho _i$ and $\gamma _a$ for the novel coronavirus model (1). These six parameters value and the initial individuals size plays a critical role in the model analysis.

Fig. 3

Quantification of semi-relative sensitivity analysis by computing sensitivity coefficient using $L_2$ norm

Sensitivity analysis depicts the significance of parameter alters in the model output. Due to the lines of Martin Fink [60], we draw the sensitivity graph by utilizing the code myAD, established by Fink [60] (see Fig. 2). To quantify the sensitivities of the parameters from Fig. 2, we calculate the sensitivity coefficient by calculating $L^2$-norm that can be defined as follows:

$$\begin{aligned} C_{ij}= & {} \left\| \frac{\partial x_i}{\partial q_j} \frac{q_j}{\max x_i} \right\| _{2}^{2} ~=~ \int _{t_0}^{t_f} \left| \frac{\partial x_i}{\partial q_j} \frac{q_j}{\max x_i} \right| ^{2}\mathrm{d}t. \end{aligned}$$

From the computation of $L^2$-norm, it is clear that the most effective parameters are $\beta _s$, $\alpha _a$, $\delta$, $\sigma _a$, $\rho _i$ and $\gamma _a$ in descending order (see Fig. 3) by comparing and ranking the sensitivity function that represents the other model parameters are less sensitive with respect to the clinically ill or symptomatic infected population, thus they will affect the dynamics of novel coronavirus a little.

A parameter is known as practically identifiable if an individual estimate can be determined from various initial conditions utilizing the available data. We consider Fisher’s information matrix $F = S^{T}S$, where S represents the normalized sensitivity matrix calculated by automatic differentiation [60]. It can be noticed that m parameters are said to be locally identifiable iff the column rank of the matrix S = m, or identically $\det (S^{T}S) \ne 0$. After that, we execute QR factorization method with column pivoting in MATLAB routine qr, $[Q, ~R, ~P] ~=~ qr(F)$. This procedure find out matrix P in such a way that $FP=QR$ (QR is the factorization of FP). This indices in first k columns of P recognize k parameters are most estimable. In our study, $\beta _s$, $\alpha _a$, $\delta$, $\sigma _a$, $\rho _i$ and $\gamma _a$ are the model parameters that are most estimable from the novel coronavirus data. We have estimated the most sensitive parameters by using least square method, after identifying them. The values of these parameters are provided in Table 2. We have estimated the data for 110 days (from February 01, 2021 to May 21, 2021). The numerical procedures and data used for parameter estimation are given in the supplementary material. Model fitting is shown in Fig. 4.

Fig. 4

Parameter estimation for the novel coronavirus model system (1) based on data from India. The SAIQJR model fitted with the real data for the daily new confirmed COVID-19 cases and the cumulative confirmed COVID-19 cases of India for the time period February 01, 2021 to May 21, 2021 (110 days). Real data are shown in blue circles, whereas the red curve represents the best fitting curve of the system (1). Parameters are used for numerical solution and specified in Table 2. The initial size of the individuals used for numerical simulation are given in the text

4.2 Model calibration

We calibrated the proposed SAIQJR model by fitting the daily COVID-19 infections and cumulative COVID-19 cases in India from February 01, 2021, to May 21, 2021 (110 days). We used the nonlinear least squares method to minimize the root-mean-squared error (RMSE) between model-simulated and reported data. Due to the varied orders of magnitude of data, we standardized these data for the same orders of magnitude by dividing by the max value of the data sets, which could avoid the fitting process automatically skewing larger orders of magnitude data and better match each type of data. We estimated six most effective parameters (identified through sensitivity analysis) by data fitting and obtained the other model parameters from the published literatures (see Table 2).

To measure the accuracy of our model fitting, we have computed mean absolute error $(E_\mathrm{MAE})$ and root-mean-square error $(E_\mathrm{RMSE})$. The $(E_\mathrm{MAE})$ and $(E_\mathrm{RMSE})$ are defined as follows:

$$\begin{aligned} E_\mathrm{MAE}= & {} \frac{\sum _{i=1}^{n}| C(i) - S(i)|}{n}, \\ E_\mathrm{RMSE}= & {} \sqrt{\frac{\sum _{i=1}^{n}( C(i) - S(i))^2}{n}}, \end{aligned}$$

where C(i) denotes the observed value, S(i) denotes the model simulation and n is the sample size of the observed data. The value of $E_\mathrm{RMSE}$ for India is given in Fig. 4. Our model performs well in the case study of India.

4.3 Model simulation without control strategy

We performed the numerical simulations in twofolds, namely without administration of optimal control and with the administration of optimal control theory. For the validation of our theoretical analysis, we conduct some numerical simulations for the model parameters that are specified in Table 2. Due to the present situation of the COVID-19 pandemic in India, the newly infected population per unit time is represented by $\beta SI \equiv \beta _s (\alpha _aA + \alpha _i I + \alpha _j J)$. The total population in India in August 2021 is approximately 138 million, and according to the data from World Health Organization (WHO) [58], the daily confirmed number of infected cases on February 01, 2021, is 11,427. Thus, we have used the following set of the initial size of the populations:

$$\begin{aligned} {\mathcal {S}}\equiv & {} \bigg \{ S(0) = 1380004385, ~A(0)= 5000, \\&~I(0) = 11427, ~Q(0) = 1, ~J(0) = 10,\\&~R(0) = 1 \bigg \}. \end{aligned}$$

Fig. 5

Tornado plot for normalized forward sensitivity indices of the model parameters related with basic reproduction number $R_0$ are listed in Table 1 indicating that the most sensitive parameters are $\beta _s$, $\Lambda _s$ and $\delta$

Figures (Fig. 6a–d) represent the contour plots that demonstrate the dependence of the basic reproduction number $R_0$ with respect to $\beta _s$ (disease transmission rate) and $\sigma _a$ (progression rate of infected individuals); $\alpha _a$ (adjustment factor for clinically ill population) and $\sigma _a$; $\alpha _j$ (fraction of isolated or hospitalized individuals) and $\sigma _a$; $\alpha _a$ and $\beta _i$ (infected individuals progress to isolated class) for India. From Fig. 6a, we noticed that for an increasing value of disease transmission rate $\beta _s$ and $\sigma _a$, the value of the basic reproduction number $R_0$ increases. Similar phenomena has been noticed from Fig. 6b–d. Thus, from Fig. 6a, we can conclude that in order to mitigate the transmission of SARS-CoV-2, the basic reproduction number $R_0$ need to be maintained and that can be possible by maintaining the social distancing as well as contact tracing.

Fig. 6

Contour plots of the basic reproduction number $R_0$ for the case of India. a Contour plot of $R_0$ as a function of $\beta _s$ and $\sigma _a$; b Contour plot of $R_0$ as a function of $\alpha _a$ and $\sigma _a$; c Contour plot of $R_0$ as a function of $\alpha _j$ and $\sigma _a$; d Contour plot of $R_0$ as a function of $\alpha _a$ and $\beta _i$. All parameter values other than (a) $\beta _s$ and $\sigma _a$; (b) $\alpha _a$ and $\sigma _a$; (c) $\alpha _j$ and $\sigma _a$; (d) $\alpha _a$ and $\beta _i$ are specified in Table 2

As we are familiar with that the numerical value of $R_0$ describes the behavior of the infectious diseases. From Table 1 and Figs. 5, 6a–d, we can see that parameters with non-positive indices can be improved, and then the magnitude of $R_0$ would be diminished substantially. The model parameters, namely $\beta _s$, $\Lambda _s$ and $\alpha _a$, has nonnegative indices, and thus mitigation of these three model parameters can control the outbreak of the COVID-19 diseases. Moreover, from the sensitivity indices, we can observe that three parameters associated with susceptible population, namely $\beta _s$, $\Lambda _s$ and $\alpha _a$, are the most effective parameters, and we can restrict positively these three parameters. Therefore, we may deduce that the most favorable method to maintain the COVID-19 diseases is to decrease the value of the parameters.

To better understand the threshold parameter $R_0$, we have drawn a surface plot for $R_0$ with respect to $\beta _s$ (disease transmission rate) and $\gamma _a$ (rate by which asymptomatic populations become recovered), and the other parameters are defined in Table 2. The expression for basic reproduction number is defined in (4), and we note that $\frac{\mathrm{d}R_0}{\mathrm{d}\beta _s} > 0$ and $\frac{\mathrm{d}R_0}{\mathrm{d}\gamma _a} < 0$. If we increase $\beta _s$, the basic reproduction number $R_0$ will increase and cross the value $R_0 = 1$, thus leading to the substantial outbreak of the SARS-CoV-2 virus. Moreover, when the recovery rate $\gamma _a$ of asymptomatic individuals increases, the basic reproduction number $R_0$ will decrease, and if $R_0$ becomes lower than 1, the infected populations will no longer persist. The surface plot shown in Fig. 7 represents the behavior of $R_0$ in the range of $\beta _s$ and $\gamma _a$. Therefore, our model illustration proposed that the recovery rate $\gamma _a$ of asymptomatic individuals aids to eliminate the novel coronavirus by decreasing the basic reproduction number $R_0$. Also, our simulations suggest that the reproduction number can be maintained by decreasing the value of the disease transmission rate $\beta _s$ and that can be obtained by maintaining social distancing and contact tracing.

Fig. 7

Surface plot of $R_0$ as a function of $\beta _s$ (disease transmission rate) and $\gamma _a$ (the rate at which asymptomatic individuals become recovered). All parameter values other than $\beta _s$ and $\gamma _a$ are given in Table 2

Fig. 8

Comparisons of the corresponding to the (a) asymptomatic infected cases, (b) clinically ill or infected individuals, (c) quarantine individuals, (d) hospitalized or isolated individuals without intervention strategies, with the implementation of intervention strategies (combination of three controls and single controls). Optimal treatment strategy (solid blue line) demonstrates substantial reduction in all the state solutions when compared with the no controls and the application of single controls. The parameter values are given in Table 2 when $R_0=1.8469$

4.4 Model simulation with control strategy

Now, we introduce additional recovery through the medication by using the theory of optimal control problem. In the model system (9), we have introduced three different control policies to mitigate the transmission of COVID-19 burden and to minimize the total cost by obtaining the optimal control paths. We performed numerical simulations to investigate these outcomes and also to observe the influence of different parameters and intervention strategies on the transmission dynamics of COVID-19. To investigate the numerical simulation of the objective functional (10) subject to the coupled system of ordinary differential equations (9), we utilize fourth-order Runge–Kutta method with the aid of MATLAB. We solve the co-states (11) by using backward Runge–Kutta method by employing the solutions of (9) with the transversality conditions defined in Theorem 6. After that, these controls are upgraded for the optimality utilizing the Hamiltonian of the optimal system. To do this, we used the steepest descent method of optimization that has been studied in [55, 56]. The time frame of investigation and implementation of the optimal control strategies is considered to be 400 days. To solve the controlled system and the corresponding adjoint system, we use the parameters set defined in Table 2.

Fig. 9

Comparisons of the corresponding to the (a) asymptomatic infected cases, (b) clinically ill or infected individuals, (c) quarantine individuals, (d) hospitalized or isolated individuals without intervention strategies, with the implementation of intervention strategies (combination of three controls and combination of two controls). Optimal treatment strategy (solid blue line) demonstrates substantial reduction in the cases in all the state solutions when compared with the no controls. The parameter values are given in Table 2 when $R_0=1.8469$

To analyze the impact of optimal treatment policies for the transmission dynamics of novel coronavirus, we employ different control policies for the disease compartments, namely asymptomatic population, clinically ill population, quarantine populations and the isolated individuals. In general, high basic reproduction number ($R_0 > 1.8469$) create epidemics with high epidemic peak. Figure 8a–d represents the impact of each treatment strategies on the disease state variables in the presence of optimal control as well as without optimal controls when $R_0$ = 1.8469. These plots demonstrates the asymptomatic cases, daily number of infected cases, quarantine individuals and the isolated or hospitalized cases under no control $(\eta _1(t)=\eta _2(t)=\eta _3(t)=0)$, with the combination of three different controls $(\eta _1(t), \eta _2(t), \eta _3(t))$ and for single controls $\eta _i(t)$ where $i=1, 2, 3$. The solid red curves for epidemic (without administration of intervention strategies) are exhibited to highlight the difference from those created via implementation of optimal treatment polices. The solid blue epidemic curves (with the implementation of three controls) are shown the significant reduction in the asymptomatic cases, clinically ill cases, quarantine cases and isolated cases when compared with the no intervention scenario. The solid magenta curves, solid green curves and solid black curves represents the single controls, namely $\eta _1(t),$ $\eta _2(t)$ and $\eta _2(t)$, respectively, shows the reduction in the asymptomatic cases, clinically ill cases, quarantine cases and isolated cases when compared with the no intervention strategies as well the implementation of three controls. Implementation of single control is better in comparison with the without control policy. Also, in the cases for asymptomatic cases (only $\eta _1(t)$), clinically ill cases (only $\eta _2(t)$), quarantine cases (only $\eta _1(t)$) and isolated or hospitalized cases (only $\eta _3(t)$) show the significant reduction in the individuals when compared with the no intervention scenario and compared with the implementation of three controls. Thus, from Fig. 8a–d, we can conclude that the implementation of intervention strategy has an impact in controlling the transmission dynamics of novel coronavirus epidemic.

Fig. 10

Optimal control functions as a function of time corresponding to the (a) three controls ($\eta _1(t)$, $\eta _2(t)$ and $\eta _3(t)$); (b) two controls ($\eta _1(t)$ and $\eta _2(t)$); (c) two controls ($\eta _1(t)$ and $\eta _3(t)$); (d) two controls ($\eta _2(t)$ and $\eta _3(t)$). Parameters are given in Table 2

Fig. 11

Optimal control functions as a function of time corresponding to the single control (a) $\eta _1(t)$, (b) $\eta _2(t)$ and (c) $\eta _3(t)$. Parameters are given in Table 2

Now, we employ different treatment strategies for the disease compartments, namely asymptomatic individuals, symptomatic or clinically ill population, quarantined cases and the isolated individuals. The time series Fig. 9a–d represents the impact of each treatment strategies on the disease state variables in the presence of the optimal control strategy and in the absence of optimal treatment strategy for $R_0 = 1.8469$. These plots demonstrate the asymptomatic cases, daily number of infected cases, quarantine individuals and the isolated or hospitalized cases under no control $(\eta _1(t)=\eta _2(t)=\eta _3(t)=0)$, with the combination of three different controls $(\eta _1(t), \eta _2(t), \eta _3(t))$ and the combination of two controls, namely $\eta _1(t)$ and $\eta _2(t)$; $\eta _1(t)$ and $\eta _3(t)$; $\eta _2(t)$ and $\eta _3(t)$. The solid red curves for epidemic (without implementation of intervention strategies) are shown to highlight the difference from those created via administration of optimal treatment polices. The solid blue epidemic curves (with the administration of the combined of three controls) are exhibited the significant reduction in the asymptomatic cases, clinically ill cases, quarantine cases and isolated cases when compared with the no intervention strategies. The solid magenta curves, solid green curves and solid black curves denotes the combination of two controls, namely $\eta _1(t)$ and $\eta _2(t)$; $\eta _1(t)$ and $\eta _3(t)$; $\eta _2(t)$ and $\eta _3(t)$, respectively, shows the reduction in the asymptomatic cases, clinically ill cases, quarantine cases and isolated cases when compared with the no intervention strategies as well the implementation of three controls. Implementation of the combination of two controls is better when compared with the no control policy. Also, in the cases for asymptomatic cases (when $\eta _1(t)$ and $\eta _3(t)$), clinically ill cases (when $\eta _1(t)$ and $\eta _2(t)$), quarantine cases (when $\eta _1(t)$ and $\eta _3(t)$) and isolated or hospitalized cases (when $\eta _1(t)$ and $\eta _3(t)$) shows the significant reduction in the individuals when compared with the combination of three controls. Thus, from the numerical simulations (Fig. 9a–d), we can infer that the implementation of intervention strategy has an impact in controlling the transmission dynamics of novel coronavirus epidemic. Also, we can conclude that the combination of two controls are more effective when compared with the implementation of the single control. It can also be noted that combination of three controls are more effective when compared with the combination two controls as well as single controls.

The control functions $\eta _2(t)$) and $\eta _3(t)$) represents the antiviral treatment effectiveness aimed at clinically ill or infected cases and hospitalized or isolated populations, respectively. Another control function $\eta _1(t)$) maintains the mitigation of the creation of secondary infected cases resulting from the isolated individuals. The numerical results for the controls are shown in Fig. 10a–d. The numerical solutions of the implementation of three control effectiveness are simultaneously shown in Fig. 10a. Corresponding to the implementation of the combinations of two controls, namely controls $\eta _1(t)$) and $\eta _2(t)$); $\eta _1(t)$) and $\eta _3(t)$); $\eta _2(t)$) and $\eta _3(t)$) are shown in Fig. 10b–d, respectively. The plot of the three graphs (see Fig. 11) represents the optimal control functions where single control strategies, namely $\eta _1(t)$, $\eta _2(t)$ and $\eta _3(t)$ have been implemented. The optimal control strategies based on single controls need the administration of in-depth effectiveness at the starting of an outbreak (Fig. 11a–c) of the novel coronavirus followed by quick reductions (most likely the outcome of high reduction in the levels of susceptible individuals).

5 Discussion

Mitigating the impact and spread of the ongoing novel coronavirus pandemic was on the minds of every newscaster, Govt. official, public health departments, aspiring politicians and literally millions of populations throughout the world within a couple of months ago. According to the report by WHO, about 22 crore populations are infected with the novel coronavirus throughout the world [58]. Though the Govt. of different countries and clinicians of each and every country are trying to give safeguards to the individuals, still the rate of infection is high due to absence of proper vaccination for the COVID-19 virus. After the Second World War, the world has never gone through like the current situation that arrived due to novel coronavirus pandemic. Beginning from the Wuhan city of China in December 2019, the SARS-CoV-2 has outspread throughout the world. Due to the absence of proper antiviral or effective treatment of novel coronavirus, one can rely on the qualitative control of novel coronavirus disease in spite of the elimination. In the absence of proper vaccination and with an incomplete understanding of epidemiological cycle, mathematical models may help in understanding of both novel coronavirus transmission and its control.

To keep this pandemic scenario in our mind, we proposed and studied a compartmental SAIQJR model for novel coronavirus. Theoretical as well as numerical analysis of model system has been investigated using stability theory. Positivity and boundedness of the state equations assured that the proposed model (1) is well-defined. Our model system (1) possess two equilibrium points, namely a unique disease-free fixed point $E_0$ and a unique endemic equilibrium point $E^*$ whose feasibility and stability criteria depends on the numerical value of $R_0$. Using the theory of center manifold, we showed that the unique endemic steady state $E^*$ is locally asymptotically stable when basic reproduction number $R_0$ exceeds 1. We also performed the global stability criteria for the disease-free fixed point $E_0$ [61]. From the parameters in Table 2, we obtained the basic reproduction number $R_0=1.8469$ that demonstrates the significant outbreak of the SARS-CoV-2 virus.

We calibrated our proposed model based on the daily new novel coronavirus cases and cumulative number of novel coronavirus cases of India. Our proposed model has 14 parameters, and we estimated only six parameters depends on the sensitivity analysis. As the sensitivity analysis exhibited that only six parameters are most sensitive with reference to the clinically ill or infected individuals. We also performed the normalized forward sensitivity analysis for our proposed model which reveals that the disease transmission rate $\beta _s$, recruitment rate $\Lambda _s$ of susceptible individuals, modification factor for asymptomatic individuals $\alpha _a$ and the mortality rate $\delta$ of all the individuals have an impact effect on the clinically ill individuals and $R_0$. Our model illustration shows that to control the disease transmission must have to maintain the social distancing, contact tracing, avoid mass gathering and use proper sanitization.

Moreover, we have modified our SAIQJR model by introducing optimal control problem. Implementation of intervention policies aids to mitigate the COVID-19 disease burden. To investigate the influence of non-pharmaceutical and pharmaceutical intervention policies and to stop the community transmission of the SARS-CoV-2 virus, we implemented three different control measures $\eta _i(t)$ for $i= 1, 2, 3$. We established the existence of the optimal control functions. Moreover, to mitigate the infected populations and to minimize the cost of the controls, an objective functional ${\mathcal {W}}(\eta _1(t), \eta _2(t), \eta _3(t))$ has been formed and interpreted with the aid of Pontryagin’s maximum principle.

The behavioral changes in the susceptible individuals alters with time, and to prevent or limit the rate of interaction between susceptible (S) and isolated (J) individuals, we put the external effort $\eta _1(t)$ an intervention strategy. Also the clinically ill or infected individuals become aware about the coronavirus disease fatality and consult with medical officers or admit to the hospitals or nursing home if the symptom occurs and thus we use the controlling effort $\eta _2(t)$ that changes the fraction of clinically ill cases. Again, we employ the controlling effort $\eta _3(t)$ that taking into account the cost regarding proper diagnosis, use of test kits and life-saving medicines that given to the hospitalized or isolated individuals. Thus, we considered all these three control strategies in our proposed model.

Finally, through extensive numerical simulations, we conclude certain observations. Numerical simulations shows in Fig. 11a that the intervention strategy presenting behavioral response $\eta _1(t)$ efforts with high magnitude immediately after introduction but slowly it reduces with time. Another way, the control strategy representing clinically ill or infected cases $\eta _2(t)$ efforts with its high magnitude for quite a long time and then it reduces (see Fig. 11b). Later on, the controls indicating better treatment strategy for isolated individuals $\eta _3(t)$ efforts with high magnitude nearly about 3 months following a mitigation at a later stage, though this magnitude is higher than the magnitude of $\eta _2(t)$ (see Fig. 11c). From the extensive numerical simulations (see Fig. 9a–d), we can infer that the implementation of intervention strategy has an impact in controlling the transmission dynamics of novel coronavirus epidemic. Also, we can conclude that the combination of two controls are more effective when compared with the implementation of the single control. It can also be noted that combination of three controls is more influential when compared with the combination two controls as well as single controls. Thus, implementing all the three control strategies may help to mitigate novel coronavirus disease transmission at this present epidemic scenario. From medical perspective, we presume that our discussion sheds light on the dynamic model of COVID-19 transmission and its control.

It is important to point out that further monitoring is essential since other factors such seasonality of respiratory diseases might play an important role on COVID-19 transmission and control. More classified data are available, specifically the age-structured data, then more complex mathematical models would be helpful for in-depth investigation of the COVID-19 pandemic. We plan to address the new progression of the epidemic data in another piece of work in near future. We also plan to expand our modeling efforts by introducing vaccination and the effect of environment contamination. Most probably, this COVID-19 epidemic will remain in the communities for many years, so the changes we see in public health services and in human habits have to go on over time. Actions as simple as washing hand, space hygiene, social distance, contact tracing and use of face masks in closed spaces should be incorporated into education for health. The containment measures, which should be essential when epidemics arise, must be rigorously investigated and worked with families.