The impact of localization and registration accuracy on estimates of deep brain stimulation electrode position in stereotactic space

Patient Selection

We conducted a retrospective analysis of patients who underwent bilateral subthalamic nucleus (STN) electrode placement for PD at our center between 2009 and 2018. All subjects underwent a pre-operative MRI scan that served as the basis for surgical planning as well as a reference study for image co-registration (described below). All clinical data were obtained from the electronic health records; any missing data were obtained from paper charts. The study was approved by the Human Subject Research Ethics Board (HSREB) office (REB# 109045).

Imaging Acquisition and Processing

Prior to surgery, a gadolinium-enhanced volumetric T1-weighted (T1w) MRI scan was acquired (echo time = 1.5 ms, inversion time = 300 ms, flip angle = 20°, receiver bandwidth = 22.73 kHz, field of view = 26 cm × 26 cm, matrix size = 256 × 256, slice thickness = 1.4 mm, resolution = 1.25 × 1.25 × 1.50 mm; Signa, 1.5 T, General Electric, Milwaukee, Wisconsin, USA). Once surgery was complete, a postoperative non-contrast MRI or CT scan was acquired for the purpose of localizing the DBS electrode.

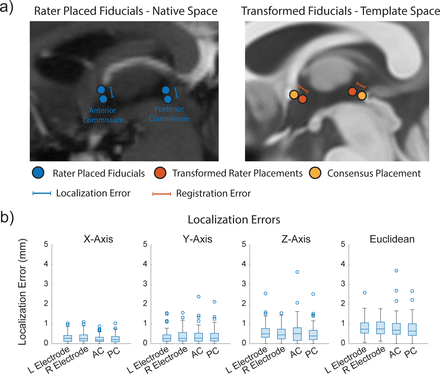
Four raters independently localized DBS electrodes using Lead-DBS software (v.2.3.2) using default settings (Horn & Kühn, 2015). Each patient had two raters independently complete the Lead-DBS workflow, raters were divided in pairs (MA/GG as raters 1, and BS/AC as raters 2, respectively). Within Lead-DBS, each patient’s postoperative CT or MRI was linearly registered to the preoperative MRI as implemented in Advanced Normalization Tools (ANTs; Avants et al., 2008; “http://stnava.github.io/ANTs/”). The two volumes were then nonlinearly registered to the MNI152NLin2009bAsym (MNI) space using the SyN registration approach in ANTs (see Table S1 for specific parameters). Nonlinear deformation into stereotactic (template) space was achieved in five stages: following two linear (rigid followed by affine) steps, a nonlinear SyN registration stage was followed by two nonlinear SyN registrations that consecutively focused on the area of interest as defined by subcortical masks (Schönecker et al., 2009). DBS electrodes were automatically pre-localized using Lead-DBS, and manually adjusted by each rater. Raters subsequently localized the anterior commissure (AC) and posterior commissure (PC) on the patient’s preoperative MRI, as defined by clinical practice (Horn et al., 2017). In addition, AC and PC were defined by consensus among raters in MNI space with the following coordinates (x,y,z): AC (−0.24, 1.88, −4.75) and PC (−0.06, −24.68, −2.36), visualized in Figure 1a.

• Download figure
• Open in new tab

Figure 1. Summary of methodology with localization accuracy of deep brain stimulation electrodes and anatomical fiducials

(a) Schematic depicting localization error and registration error. Localization error is shown as the distance between rater placed coordinates within a subject’s native space, and registration error is shown as the displacement between raters’ transformed coordinates (Transformed Rater) to rater placed coordinates (Consensus) in MNI space. (b) Localization errors of DBS electrodes, intraventricular anterior commissure (AC) and posterior commissure (PC) obtained in each axis, and the Euclidean localization error. There were no significant differences in localization error between electrode, AC, and PC LEs in all axes (Wilcoxon Sign-Rank Test (n=89), alpha = 0.05/6 in each axis).

We previously reported and openly released AFIDs annotations in a population of thirty-nine patients undergoing STN DBS for PD (Abbass et al., 2022; Taha et al., 2023). Briefly, 5 raters localized AFIDs on subject scans and on the MNI template. We non-linearly registered these volumes using fMRIPrep v1.5.4 (Esteban et al., 2019), using the SyN registration approach in ANTs. See Table S1 for a summary of the parameters used in the Lead-DBS and fMRIPrep pipelines.

Localization and Registration Accuracy

Each patient had their DBS electrode contacts, AC, and PC localized by two raters in native space representing Cartesian coordinates (x, y, and z axes) from which metrics of accuracy were computed. Specifically, the absolute difference (Euclidean distance) between rater placements was calculated and termed the localization error (LE). We compared LEs of DBS electrodes, AC, and PC using a Wilcoxon signed-rank test, and used a Bonferroni correction for multiple comparisons in each axis. Each rater’s manually placed AC and PC were then transformed to MNI space. We calculated the displacement between each rater’s transformed AC and PC to the consensus placement across the x, y, and z axes, and the Euclidean distance, a metric of registration accuracy that we call the anatomical fiducial registration error (AFRE). Figure 1a provides an illustration summarizing the calculation of LE and AFRE. We compared LEs and AFREs obtained using a Wilcoxon signed-rank test. AFRE was computed in a similar manner for a subset of patients who had the AFIDs protocol completed. We calculated the mean AFID coordinates across raters for each subject and applied the transforms obtained from Lead-DBS v2.3.2 to MNI space to compute AFRE as previously defined (Lau et al., 2019). We performed the same analysis using the transforms obtained from fMRIPrep v1.5.4. AFREs were compared using a Wilcoxon signed-rank test with Bonferroni correction to the number of AFIDs. AFIDs with a p-value less than 0.05, but that did not meet thresholds of statistical significance were also highlighted.

Correlating AFRE and Electrode Position

AFREs provide vectors of registration error in both magnitude and direction at fiducial locations rather than specific points of interest, such as an electrode contact. Across subjects, different AFREs may covary if there are consistent patterns of misregistration. Additionally, variance in electrode tip position in stereotactic space may be explained by AFREs. To this end, we investigated whether AFREs obtained at AC and PC were correlated with DBS electrode positions in stereotactic space. We centered the electrode tip locations by subtracting each patient electrode tip coordinate from the mean coordinate of all electrode tips. The displacement of each subject’s electrode tip from the mean electrode tip location was correlated with the AFRE obtained in AC and PC, and for each x, y, and z axis. We performed a simple linear regression to measure the displacement in electrode position explained by AFRE in each axis and used a Bonferroni correction for multiple comparisons for each AFID. We also explored other potential explanatory variables, including age, disease duration, sex, rater pair, modality (post-operative CT or MRI used), electrode side and implantation order. These variables were individually tested using univariate non-parametric tests, using a Wilcoxon rank sum test for binary variables (sex, rater pair, modality, side and implantation order) and a Spearman’s rank correlation for continuous variables (age and disease duration). A Bonferroni correction for multiple comparisons for each explanatory variable. A multivariate linear regression was also used including all variables and AFREs at AC and PC.

We further analyzed a subset of AFIDs which were found to explain a significant amount of variance in the electrode tip position. We first performed principal components analysis (PCA) on individual AFREs obtaining three orthogonal unit vectors (principal components; PrCs), representing the independent axes explaining the variance of AFREs. We performed this same analysis on the displacement of the electrode tip. To explore the relationship between AFREs, we computed a correlation matrix by performing simple linear regressions between all pairwise AFREs across the x, y, and z axes. The same analysis was performed with AFREs projected along their PrCs. Finally, we obtained high-dimensional axes explaining consistent variance across these AFIDs by performing PCA on all axes of the AFIDs used (3 axes x 4 AFIDs, or 12 features). We examined whether AFREs projected onto these PrCs were correlated with the electrode tip positions using a simple linear regression.

Analysis and Data Availability

All raw and processed data along with processing scripts used for data analysis (MATLAB 2022a) used in this manuscript are available at https://github.com/afids/afids-dbs.

Patient Demographics

Data from 89 patients implanted with bilateral STN DBS successfully underwent the Lead-DBS protocol independently by two raters for electrode localization. These patients had a mean age of

60.54 ± 6.12 years, a mean disease duration of 11.01 ± 4.21 years, and 31 were female (31.46%). Of these patients, 24 had the AFIDs protocol previously completed (Abbass et al., 2022). See Table S2 for a summary of the demographic variables of these patient populations.

Localization Accuracy

We first sought to investigate the accuracy and reliability of raters localizing DBS electrodes, the anterior commissure (AC), and the posterior commissure (PC) by calculating the absolute difference between the two rater placements in each axis and across all axes (Euclidean error). Figure 1b summarizes the LE for each electrode tip, AC, and PC (see Table S3 for a complete summary of LEs). The median Euclidean LE (with interquartile range; IQR) was 0.73 mm (0.53-1.06 mm) for the right electrode tip, 0.74 mm (0.50-1.10mm) for the left electrode tip, 0.68 mm (0.48-1.03 mm) for AC, and 0.63 mm (0.41-1.01 mm) for PC. A Wilcoxon signed-rank test revealed no significant differences between any LEs in all axes. Furthermore, we expanded our analysis to a subset of 24 patients who previously had AFIDs placed by five raters (Abbass et al., 2022; Lau et al., 2019; Taha et al., 2023). The median AFLE (IQR) ranged from 0.56 mm (0.40-0.69 mm) for AFID02 (PC) to 2.25 mm (1.49-2.75 mm) for AFID25 (right inferior anteromedial temporal horn). See Abbass et al. (2022) for more details.

Registration Accuracy

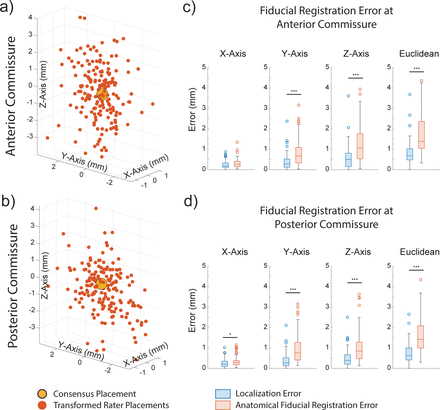
So far, we have described our calculation of LE, which represents a measure of the accuracy and reliability of electrode localization; however, registration to stereotactic space introduces additional error. To capture a fiducial-based measure of this error at the AC and PC locations, rater-placed coordinates were transformed to MNI space. AFREs are visualized as a 3D point cloud centered around the consensus placement (Figures 2a/b) and summarized in Table S4. The median Euclidean AFRE with IQR was 1.39 mm (1.05-2.38 mm) for AC (Figure 2c) and 1.42 mm (1.00-2.10 mm) for PC (Figure 2d). Compared to LE at AC and PC, AFREs at these locations were significantly greater in the y and z axes (Wilcoxon signed-rank Test; Figure 2c/d). The same AFREs at AC and PC were independently obtained across the four raters (Figure S1).

• Download figure
• Open in new tab

Figure 2. Anatomical fiducial registration errors at anterior and posterior commissures.

(a-b) 3D scatterplots represent transformed rater placements (red) of anterior commissure (AC) and posterior commissure (PC), and the consensus placement (yellow). The displacement of each transformed rater placement from the consensus placement represents its anatomical fiducial registration error (AFRE). (c-d) Boxplots comparing AFRE to localization error (LE) at AC and PC in all axes (Wilcoxon Sign-Rank Test (n=89), * p<0.05, *** p<0.001). AFRE was significantly greater than LE at AC and PC in the y and z axes (p<0.001).

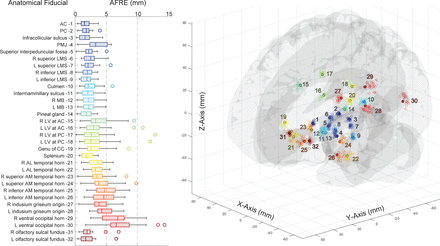
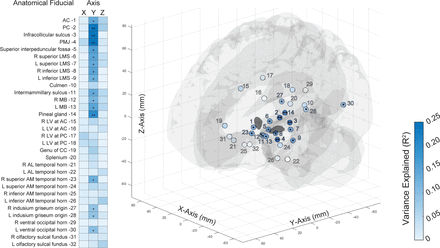
We next expanded our analysis of AFRE by using the entire set of previously defined and validated AFIDs (Abbass et al., 2022; Lau et al., 2019). Figure 3 summarizes Euclidean AFREs obtained for each AFID and illustrates 3D point-clouds of AFREs. For each subject, the mean AFRE across all AFIDs was calculated as a global measure of AFRE. The median (IQR) global AFRE was 3.09 mm (2.80-3.22 mm). AFRE was not uniform across AFIDs, with centrally located subcortical AFIDs having lower AFREs. The lowest AFREs were obtained at AFID03 (infracollicular sulcus, ICS) and AFID01 (AC) with AFREs of 1.49 mm (0.96-2.25 mm) and 1.59 mm (0.69-2.31 mm) respectively. The highest AFREs were obtained around the ventricles, the highest of which being AFID29 and AFID30 (right and left ventral occipital horn), with AFREs of 6.85 mm (4.47-7.90 mm) and 6.61 mm (5.70-8.69 mm) respectively.

• Download figure
• Open in new tab

Figure 3. Anatomical fiducial registration errors at 32 anatomical fiducials.

Boxplot of Euclidean fiducial registration errors (AFREs) calculated for 32 anatomical fiducials (AFIDs; left) and 3D scatterplot of transformed rater AFID placements (n=24; open circles) with consensus AFID placements (filled circles) in MNI space (right). Euclidean AFRE ranged from a median (with IQR) of 1.49 mm (0.96-2.25 mm) for AFID 03 to 6.85 mm (4.47-7.90 mm) for AFID 29. Subcortical and midline AFIDs had the lowest AFREs, while peripherally located and periventricular AFIDs had the highest AFREs.

In previous work, we explored AFREs obtained from these same subjects following an automated non-linear registration to MNI space using fMRIPrep 1.5.4 (Abbass et al., 2022; Esteban et al., 2019). Figure S2 summarizes the Euclidean AFREs obtained for all AFIDs using both the Lead-DBS and fMRIPrep pipelines (for the specific versions outlined). Overall, the global AFRE was higher using Lead-DBS (3.09 mm, 2.80-3.22 mm) when compared to fMRIPrep (2.75 mm, 2.46-3.01 mm; p = 0.002). This difference was not homogenous across AFIDs, and even with a stringent Bonferroni correction, 2 AFIDs had lower AFREs when using Lead-DBS: AFID14 (pineal gland, PG), and AFID20 (splenium). However, 7 AFIDs had higher AFREs using Lead-DBS: AFID01 (AC), AFID04 (pontomedullary junction, PMJ), AFID05 (superior interpeduncular fossa), AFID16 (left lateral ventricle at AC), AFID21 (right anterolateral temporal horn), AFID25 (right inferior anteromedial temporal horn), and AFID26 (left inferior anteromedial temporal horn). When we compared these AFIDs visually (Figure S2), we could appreciate that subcortical AFIDs closer to the midline were comparable, but more peripheral AFIDs had lower AFREs using fMRIPrep.

DBS Electrode Tip Position

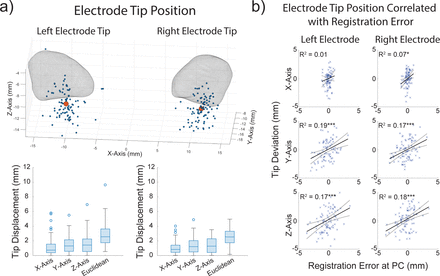
We analyzed AFREs at various anatomical landmarks; however, in the context of DBS studies, registration error should ideally be measured at the location of the electrode. We first sought to determine if the AFRE acquired at AC and PC could explain electrode position variation in stereotactic space. Figure 4a shows the distribution of electrode tips in MNI space with a mesh of the STN superimposed to provide anatomical context (Ewert et al., 2018). As a measure of electrode tip variance, we calculated each subject’s displacement from the mean electrode tip position in all axes and the Euclidean displacement (Figure 4a). The median (IQR) Euclidean displacement was 2.50 mm (1.74-3.33 mm) for the right electrode, and 2.46 mm (1.74-3.44 mm) for the left electrode. Variance of electrode position explained by AFRE at AC and PC is summarized in Table 1. A significant amount of the electrode tip displacement was explained by AFREs at both AC and PC. Electrode tip displacement in the y and z axes was especially well explained by AFRE at PC, with 19% and 17% of the variance in the y axis explained, and 17% and 18% of the variance in the z axis explained for the left and right electrode tips respectively (Figure 4b). These same patterns remained when using a Spearman’s rank correlation (Figure S3). Electrode tip displacement could not be explained by other demographic variables (Figure S3 and Table S5). Electrode displacement was not correlated with age or disease duration in any axis (Spearman’s rank correlation) and was not significantly different between sex, rater pair, modality, side, or implant order (Wilcoxon rank sum test). Finally, including all variables with AFRE in a multivariate linear regression did not change the results (Table S4).

• Download figure
• Open in new tab

Figure 4. Electrode position in template space is explained by registration error.

(a) 3D scatterplot of all deep brain stimulation (DBS) electrode tip positions (blue, n = 89) and the mean electrode tip position (red) in MNI space, with a mesh of the subthalamic nuclei (Ewert et al., 2018) overlayed (top). Boxplots of each electrode tip’s displacement from the mean electrode tip position in all axes. (b) Correlating left and right electrode tip position with registration error at the posterior commissure (PC) in all axes, (Simple linear regression (n=86), * p<0.05, *** p<0.001). There was a significant correlation between AFRE at PC in the y and z axes and electrode tip displacement in those axes (p<0.001).

Subcortical AFIDs Correlated with Electrode Position

We next explored whether AFREs at different AFIDs explained the variance of electrode tip position. For each AFID, AFREs were correlated with electrode tip displacement in each axis, as previously performed (Figure 4b). Figure 5 shows the variance of electrode tip displacement explained by AFIDs in each axis. Electrode position in the y axis was best explained by registration error for subcortically located AFIDs. Four AFIDs were significantly correlated with electrode tip position after multiple comparison corrections: AFID02 (PC; 1.80 mm, 1.19-2.25 mm), AFID03 (ICS; 1.59 mm, 0.69-2.31 mm), AFID04 (PMJ; 3.28 mm, 2.37-5.19 mm), and AFID14 (PG; 1.80 mm, 0.94-2.57 mm).

• Download figure
• Open in new tab

Figure 5. Electrode position in template space is explained by registration errors of anatomical fiducials close to the subthalamic nucleus.

Heatmap of electrode tip position variance explained (R²) by anatomical fiducial registration error, (Simple linear regression (n=48), * p<0.05, ** p<0.05/32; left) and 3D scatterplot of 32 AFIDs color mapped by R² in the y axis with significance indicated (right). Subcortical AFIDs in close proximity to the electrode target (subthalamic nucleus) had AFREs more correlated with electrode displacement. Specifically, four AFIDs had AFREs significantly correlated (p<0.05/32) with electrode tip displacement in the y axis: AFIDs 02 (posterior commissure, PC), 03 (infracollicular sulcus, ICS), 04 (pontomedullary junction, PMJ), and 14 (pineal gland, PG).

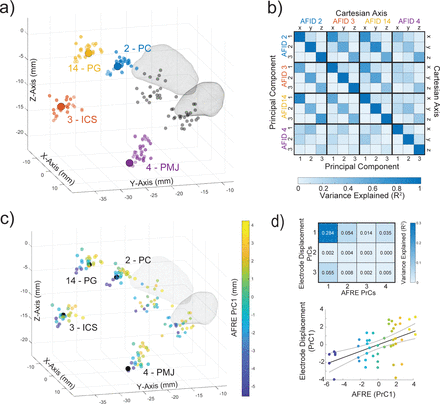
To further understand these correlations, we analyzed AFREs at the identified locations using PCA. Figure 6a illustrates these AFREs and tip positions as 3D point clouds in MNI space. AFREs at AFID02, AFID03, and AFID14 had a similar 3D distribution, with almost identically oriented PrC axes (Table S6). Furthermore, AFREs at these AFIDs were strongly correlated along their PrCs (Figure 6b), with the variance explained ranging between 48% to 85% (p<0.001 for all correlations across PrCs). AFID04 had a different AFRE distribution, with a greater contribution from the Cartesian z axis to its first PrC (Table S6). The AFRE for AFID04 was less correlated with AFREs for AFID02, AFID03, and AFID14 (Figure 6b). Given this strong covariance of AFREs, we performed PCA across all axes of these four AFIDs (i.e. 12 features), and the top 4 PrCs explained 89% of the total variance. The first PrC largely weighed the y axes of AFID02, AFID03, and AFID14, and a combination of the y and z axes of AFID04. The second PrC placed a greater weight on the z axis of AFID04, suggesting the presence of a component of registration error unique to this AFID.

• Download figure
• Open in new tab

Figure 6. Registration errors covary across a set of subcortical anatomical fiducials close to the DBS target and explain the largest component of variance in electrode position.

(a) 3D scatter plot in MNI space with each subject’s transformed anatomical fiducial placements: AFID 02 (posterior commissure, PC), 03 (infracollicular sulcus, ICS), 04 (pontomedullary junction, PMJ), and 14 (pineal gland, PG). The large solid points represent the consensus placements in MNI space. The black transparent points represent the transformed placements of each subject’s left and right electrode tips, with a mesh of the subthalamic nucleus (Ewert et al., 2018). (b) Correlation matrix of AFREs across four AFIDs (left), shown in both standard Cartesian coordinates (top right) and along each AFID’s PrCs (bottom right). (c) PCA across all AFID axes (12 features) was performed, and AFRE was projected on the first PrC. Each subject’s AFRE along the first PrC was linearly mapped to a Parula colour map and projected on a 3D scatter plot in MNI space. (d) Correlation matrix of the top four AFRE PrCs with the electrode tip displacement projected onto its PrCs (top) and scatterplot of AFID AFREs and electrode tip displacement along their first PrCs (bottom).

Finally, we sought to determine if these observed patterns of AFREs across independently placed AFIDs explained the variance observed in electrode position. The first PrC of AFREs is illustrated in Figure 6c, which colour maps each subject’s AFRE along this PrC. Next, we performed PCA on the electrode tip displacements, demonstrating a 3D distribution similar to AFID02, AFID03, and AFID14 (Table S6). We correlated electrode position along its PrCs to AFREs along their top four PrCs (Figure 6d). The first PrC of electrode position was significantly correlated with the first PrC of AFREs, with 28.4% of the electrode tip variance along the first PrC explained (p<0.001). Across all 48 electrodes, this corresponds to a median (range) of 0.64 mm (0.02-2.05 mm) of error in electrode position that can be explained by AFRE.

Localization Accuracy

Accurate localization of DBS electrode contacts is essential to study the effects of DBS. Despite this, to our knowledge there was only one study that has investigated the reliability of contact localization (Lofredi et al., 2022). We replicate these results (LE ranging from 0.52 mm to 0.75 mm) using the Lead-DBS pipeline, obtaining a median Euclidean LE of 0.73 mm and 0.74 mm for the right and left electrodes respectively. The slightly higher error may be a consequence of the current study using mostly post-operative MRIs to localize DBS electrodes (78.7%) and having two raters rather than five raters reported by Lofredi et al. (2022). Additionally, we directly compared electrode localization error to LEs obtained at AC (0.68 mm) and PC (0.63 mm). Overall, these results demonstrate that DBS electrode contacts can be as accurately localized as routinely used stereotactic landmarks, roughly within the scale of a voxel on clinical imaging.

Registration Accuracy

Beyond electrode localization, accurate registration of individual images to stereotactic space is a common step in neuroimaging studies investigating group or population-level effects (Barow et al., 2014; Horn et al., 2017; Jeon et al., 2022). This can be particularly important in studying DBS, where clinical effects depend on millimetric accuracy (Kremer et al., 2023; Zhang et al., 2021). To this end, there has been important work to optimize the accuracy of registering individual images to stereotactic space, particularly in subcortical structures (Avants et al., 2010; Ewert et al., 2019; Schönecker et al., 2009). Measures of accuracy have typically relied on voxel overlap measures, like the Jaccard similarity and Dice kappa coefficients (Ewert et al., 2019; V. S. Fonov et al., 2009; Rohlfing, 2012; Vogel et al., 2020). Fiducial based metrics, such as AFRE used in the current study, have rarely been investigated in the context of stereotactic registration, but have the advantage of providing millimetric estimates of registration accuracy. We previously demonstrated that individual fiducials can be quickly placed (of which AC and PC are generally already identified for DBS procedures by the surgical team) and can capture misregistration not observed with voxel overlap metrics (Lau et al., 2019; Miller et al., 2023). Motivated to quantify AFRE in a population of patients who underwent STN DBS for PD, we used our manual placements of each subject’s AC and PC obtaining median AFREs of 1.39 mm and 1.42 mm at AC and PC respectively. This was significantly higher than the LEs at these locations, on an order of two to three times the LE. Therefore, AFRE adds a substantial degree of variance compared to localization error, consistent with previous work (Abbass et al., 2022). We then expanded our analysis to investigate 32 previously identified AFIDs, demonstrating AFREs ranging from 1.49 mm to 6.85 mm with subcortical AFIDs at the midline having the lowest AFREs, which are closest to the conventional targets for DBS.

It is difficult to compare the AFREs we obtained given the limited reports of fiducial-based metrics for evaluating registration from subject to stereotactic space. The initial study describing the AFIDs framework found AFREs ranging from 0.36 mm to 4.51 mm (Lau et al., 2019). The higher AFREs obtained in the current study was expected given the use of clinical images. We subsequently explored AFREs in a set of patients undergoing DBS for PD using non-linear registration (Abbass et al., 2022); a subset of these patients who were also included in the current study, giving us an opportunity to provide proof-of-concept comparison of two commonly used open-source pipelines for neuroimaging analyses: fMRIPrep and Lead-DBS (see Table S1 for details). Key differences between these pipelines include additional nonlinear SyN registrations that consecutively focused on optimization of registration of subcortical areas, a process termed “subcortical refinement” in Lead-DBS (Ewert et al., 2019). We found that the majority of midline and subcortical AFIDs had similar AFREs using both pipelines, but the Lead-DBS pipeline had decreased AFREs for midline AFIDs located more posteriorly (the pineal gland and splenium). This difference was presumably due to the additional subcortical refinement in Lead-DBS, which aims to provide more accurate registration in anatomically relevant regions for DBS (Ewert et al., 2019). Of note, this comparison was not meant to be exhaustive but rather to be used as an example to demonstrate the utility of the AFIDs framework for providing focal (millimetric) estimates of differences between software versions and packages.

There are limited reports of other groups providing fiducial-based metrics for registration accuracy. Schönecker et al. (2009) computed fiducial-based metrics for their novel registration algorithm using a linear three-step registration focusing on the basal ganglia. The authors computed the root-mean-square error (RMSE) across Cartesian axes for 16 fiducials, rather than the Euclidean-based metric we report. This group reported RMSEs of 1.26 ± 0.70 mm at AC and 0.93 ± 0.72 mm at PC. To directly compare with this prior work, we recomputed our measures as RMSE and obtained a similar RMSE at PC (0.92 ± 0.49 mm), and a lower RMSE at AC (0.97 ± 0.52 mm; Table S4). Horn et al., (2017) transformed rater placed AC and PC coordinates from stereotactic space to individual images and calculated the RMSE in each axis. Across AC and PC, RMSE was 0.29 mm (x axis), 1.59 mm (y axis), and 1.16 mm (z axis). In contrast, we obtained higher errors in the x axis (0.42 mm) and z axis (1.40 mm), and lower errors in the y axis (1.22 mm; Table S4). Overall, the registration accuracy we obtained in this study is in keeping with previous reports. One advantage of the AFIDs framework is that it leverages open resources and tools, developed with full transparency in mind so that others may freely use, adopt, and modify.

Registration Errors Covary with Electrode Location

The true electrode contact location for a given DBS patient in stereotactic space is unknown. Previous studies have relied on manually obtained fiducial localizations or ROI segmentations near the electrodes, indirectly measuring the effect of misregistration (Ewert et al., 2019; Lau et al., 2019; Vogel et al., 2020). The assumption that nearby anatomical structures share misregistration is inherent to this work; however, to our knowledge, the relationship of misregistration between anatomically distinct regions has not been investigated. AFRE provides a 3D metric with both magnitude and direction which can be leveraged to detect systematic patterns of misregistration between distinct AFIDs. In this study, we find that AFIDs close to each other share similar AFREs. Specifically, we observed that AFID02 (PC), AFID03 (ICS), and AFID14 (PG) had highly correlated AFREs (Figure 5c). In fact, these AFREs varied along almost identical independent axes and shared a significant amount of variance. This suggests that misregistration can be similar (in magnitude and direction) across anatomically distinct regions, adding to the validity of previous studies measuring registration accuracy.

Since AFREs across AFIDs can covary, systematic spatial patterns of misregistration may explain some variance in DBS electrode position. We found that our electrode tips had median (IQR) Euclidean displacements 2.50 mm (1.74-3.33 mm) and 2.46 mm (1.74-3.44 mm) for the right and left electrodes respectively. Exploring all 32 AFIDs, we found that the AFIDs closest to the DBS target of the study population (STN) explained a significant amount of variance in electrode tip position. Additionally, electrode position and AFREs at AFID02 (PC), AFID03 (ICS), and AFID14 (PG) all varied along similar independent axes. This suggested that common patterns of misregistration between these AFIDs may have influenced electrode positions. To further support this, we correlated electrode positions along their PrCs with AFREs projected onto their PrCs. We found that the first PrC of AFREs explained 28.4% of the variance in electrode tip position, representing 0.64 mm (0.02-2.05 mm). The patterns of misregistration depend on specific pipeline parameters and software versions, the impact of which can be evaluated more systematically with this framework.

Practical and Clinical Implications

Our findings have important implications for studies that answer population level questions by registering individual brain scans to a stereotactic space. This work is especially relevant for DBS and other stereotactic applications where results are pooled across multiple sites and studies, with clinical effects that depend on millimetric accuracy (Li et al., 2016). As previously discussed, variance in electrode position can be influenced by many factors including application accuracy, LE, and AFRE. Without dissociating these factors, our contacts had a median Euclidean displacement of 2.47 mm, which can be used to contextualize the LEs and AFREs we report. On average, LE of the contacts adds ∼0.75 mm of uncertainty to the contact position. Since AFRE cannot be known at the contact location, we can only speculate about the uncertainty added by misregistration. Our most accurate AFREs were in the ∼1.50 mm range, and this is likely a conservative estimate of the uncertainty in contact position specifically added by registration error. Some of this registration error (up to 2.05 mm) could be explained by regional AFIDs close to the DBS target location. Furthermore, the extent to which these multiple sources of error accrue remains poorly understood and the framework presented provides a means to uncouple the different components.

Ultimately, the main goal for most of these studies is to explain clinical outcomes by the spatial variance of the volume of tissue activated (VTA) related to application accuracy, providing clinicians with ideal targets (Barow et al., 2014; Horn, 2019; Horn et al., 2017; Zhang et al., 2021). Considering these effects on VTA analyses requires an understanding of typical DBS electrode VTAs, which have been reported to range from 30 to 116 mm³ (Chen et al., 2022; Maks et al., 2009). Assuming a spherical VTA of 100 mm³ (radius 2.89 mm), the Dice coefficients are: 0.74 for a 1 mm shift, 0.50 for a 2 mm shift, and 0.29 for a 3 mm shift. Therefore, the LEs and AFREs we observe have the potential to change more than half of the VTA in stereotactic space. Ideally, these errors are random, without any bias, as we observed with many AFREs such as with AFID02, AFID03, and AFID14 (Figure 6a), in which case this added variance may be overcome with sufficiently powered studies. Our approach using detected patterns of misregistration across AFIDs to explain variance in contact position may result in more optimal estimates of target locations.

Limitations and Future Directions

Although we can measure AFREs at validated AFIDs and correlate this with DBS electrode position, we are unable to determine if registration errors are biased at the electrode position since the ‘true’ electrode position in stereotactic space is unknown. This issue may partially be addressed by identifying and validating an anatomical landmark at or closer to the target, which can be challenging since in this case the target (STN) can be difficult to identify on the most commonly acquired clinical scans. Another limitation is our use of gadolinium-enhanced images, which have not been optimized by automated registration pipelines and thus may have higher registration errors than images without gadolinium. Despite these potential concerns about gadolinium, the AFREs we obtained are in keeping with previous work reporting registration errors (Horn et al., 2017; Schönecker et al., 2009). Furthermore, gadolinium-enhanced scans typically represent the main reference image used during stereotactic planning due to the combination of high-quality anatomical imaging, and the ability to visualize cerebral vasculature without the need for additional multimodal fusion for trajectory optimization.

AFIDs require manual placement, which takes expertise. One barrier to adoption is that placement has been perceived to be overly time-consuming, although in our experience trained raters can complete the protocol within 15-20 minutes. This motivated the open release of a curated set of manually placed AFIDs on 14 templates and 132 individual scans, including the data used in this study (Taha et al., 2023). Since we have shown that only a few AFIDs are necessary to explain variations in electrode position for STN DBS, it may be determined that only a subset may be necessary for a given indication. In fact, AC and PC are commonly already manually defined when planning a DBS procedure, and can be quickly leveraged to calculate AFREs and explain electrode position variance. Future tools can furthermore benefit from automatic placement of AFIDs, which can be easily incorporated into established open toolboxes for neuroimaging (Esteban et al., 2019; Horn & Kühn, 2015).

We compared registration accuracy in two commonly used open tools for neuroimaging analysis: Lead-DBS and fMRIPrep. We wish to emphasize that this comparison was not meant to be formal or exhaustive but to be used as a proof-of-concept of how the AFIDs framework can be employed to evaluate registration accuracy. We selected Lead-DBS given it is the most widely adopted tool for DBS electrode localization, its transparent and open development, and given the clinical context of our dataset. We furthermore selected fMRIPrep based on previous experience (Abbass et al., 2022) and given the direct development of this application from the open Brain Imaging Data Structure (BIDS) standard (Gorgolewski et al., 2016). Both Lead-DBS and fMRIPrep employ ANTS for registration on the back end (Avants et al., 2008), and have active user and support communities. Future studies can use this framework for more detailed quality control, software testing with continuous integration, optimization and comparison of different software versions and pipelines, as well as different registration algorithms.

Concluding Remarks

In summary, we used the AFIDs framework to investigate localization and registration accuracy, as well as explain variance in electrode position related to transformations to stereotactic space. The AFIDs framework is an open resource, and curated AFID placements for various imaging datasets have been released (Taha et al., 2023). Using this framework, we provide AFREs at different anatomical locations to estimate the magnitude and direction of registration accuracy. To our knowledge, these represent the first millimetric estimates of registration accuracy in DBS, allowing uncoupling of registration-related factors from other sources of variance in electrode position. Additionally, we show that AFREs can covary, identifying potential systematic spatial patterns of misregistration in a dataset, that can explain a significant portion of the variance observed in electrode positions. Accounting for these registration errors has the potential to dissociate application error from registration error in a stereotactic space, improving the spatial specificity of group-level analyses.