Abstract
Covid-19 disease, caused by SARS-CoV-2 virus, has infected over four million people globally. It has been declared as a global public health emergency by the World Health Organization. Researchers and governments are striving to do their best to fight against this pandemic. Several Mathematical models mostly based on compartmental modeling are being used for projections for Covid-19 in India. These projections are used for policy level decisions and public health prevention activities. Compartmental models are mostly used for Covid-19 projections. Unlike compartmental models, which consider population average, the Agent based models (ABM) models consider individual behavior in the models for projections. ABMs, yet rarely used for Covid-19, provide better insights into projections compared to compartmental models. We present an ABM approach with a small synthetic population of India, to examine the patterns and trends of the Covid-19 in terms of infected, admitted, critical cases requiring intensive care and/ or ventilator support, mortality and recovery. The parameters for the ABM model are defined and model run for a period of 365 days for three different non-pharmaceutical intervention (NPI) scenarios. AnyLogic platform was used for the ABM simulations. Results revealed that the peak values and slope of the curve declined as NPI became more stringent. The results could provide a platform for researchers and modelers to explore this approach for conducting ABM for Covid-19 projections with inclusion of interventions and health system preparedness.
1. Introduction
The first reported case of the novel coronavirus (Covid-19 or SARS-CoV-2) in India dates back to January 30, 2020 when it was also announced as pandemic by WHO [1, 2]. Since then, epidemic has spread across India infecting 97,028 people with 56,707 active cases, 37,271 recovered cases and 3,044 deaths as on May 18, 2020 [3]. Globally, Covid-19 is spread across 213 nations, infecting 48,33,022 people worldwide and claiming 3,17,214 lives as on May 18, 2020, posing a global health emergency [4, 5]. In a country like India having a denser population, the situation poses a serious challenge [6]. There are several underlying factors such as age, comorbidities, exposure to air pollution, amount of exposure to virus, etc., that may determine the severity of infection and rate of recovery [7, 8]. Higher transmission rate of the disease further increases the vulnerability. Reports estimate that the transmission rates range from 2.24 to 3.58 and WHO estimates transmission rates between 1.4 to 2.5 [9, 10, 11]. The behaviour of Covid-19 is found to be similar to that of Severe Acute Respiratory Syndrome (SARS) epidemic family which reduces the chance of reinfection [7, 12]. Common symptoms of Covid-19 include fever, cough and fatigue [5]. Yet, the existence of a significant proportion of asymptomatic carriers makes it a greater cause for concern as they remain unidentified and can unknowingly spread the disease to healthy people [7, 8, 13]. Travel restrictions have reduced the rate of spread of the infection [14, 15]. Other non-pharmaceutical interventions such as restrictions on public gatherings, intracity movements, etc., may flatten the curve [16]. It is important to understand the time required between exposure and complete recovery, to take timely responsive actions against Covid-19 [17].
Modeling is an effective technique to provide solutions to real-time problems because it obviates the burden of making changes to physical systems that require a lot of investment in time, cost and risks. Simulation represents a way of mapping several real-world scenarios as a model [18]. There are several mathematical models being utilized at this time for Covid-19 using compartmental models and Discrete Event Simulation (DES) [19]. Since compartmental models and DES do not account for the interactions between individual entities within the system, Agent Based Modeling (ABM) may be a better option to gain insights [19]. ABM is thought to be of a greater importance in the public health domain as it incorporates actions of individuals/ agents within the system, helping the model comprehend infection spread dynamics better [20, 21]. ABM follows a bottom-up approach i.e., the behaviour of the system is a result of behaviour of individuals, defined as agents within the system [22, 23]. ABM allows definition of factors such as age, underlying health conditions and other susceptibility factors to the agents to make each of them behave distinctly [23]. Various factors such as the data quality, disease dynamics, ever-changing social and environmental interactions, uncertainties in effects of these interventions need to be properly dealt with as they impact on the accuracy of models [24]. Mixing patterns among the agents within a system play a vital role in dynamic transmission models for close contact infections [25]. A research study based on Susceptible Exposed Infected Recovered (SEIR) predicts that the peak infections in India would be seen by the mid of May based on the spread in the US and Italy, under no lockdown conditions. The study has analyzed two scenarios that lifting lockdown by May 15 and May 30 would nullify the case tally to zero by Sep 15 and mid-June respectively [26]. The present study aims to define an ABM approach using AnyLogic 8.5.2 University edition, to examine the patterns and trends for the number of infected people, admitted people, people who might require intensive care and/ or ventilator support, mortality rate, recovery and effect of non-pharmaceutical interventions on the transmission dynamics, for the Covid-19 epidemic through an ABM approach [27].
2. Materials and Methods
The current study follows an ABM approach using AnyLogic 8.5.2 University edition to model the interaction environment [18]. Early stages of any epidemic provide only loose estimates in terms of the proportion of people who get infected and die, number of people to whom an infected individual would transmit the infection, etc. [27]. The three key components of ABM namely i) a realistic synthetic population, ii) social contact network among the agents, and iii) a disease model was considered to construct the model [24].
Synthetic population
A synthetic population is one of the commonly used approaches to represent a group of people, preserving the confidentiality of individuals. Synthetic population has statistical equivalence with the original population being represented and is indistinguishable from the census data [28]. We used a synthetic population developed for Telangana state which consists of 5,48,323 people, to demonstrate the ABM [29]. Though the synthetic population was developed for the whole state of 40 million population, we have used a subset (one district) population for this approach to limit the compute infrastructure needed. Age was a major parameter considered to distinguish the population as it was identified as one of the key factors in determining the number of people each individual would contact, the probability of acquiring the infection, growth rate of the infections and recovery rate [7, 25]. Table S1 represents the age-wise distribution of the population.
Transmission rates of Covid-19
Based on the WHO report on Covid-19 (16 to 24 Feb 2020), the transmission rates were derived based on the statistics obtained from three cities in China [30]. The number of close contacts traced and the proportion who were infected are presented in the table S2.
To determine the distribution that the transmission rates follow, the transmission rates of table S2 were given weightages based on their respective total number of close contacts i.e., number of values corresponding to 2.8% of 2842, 0.9% of 25492 and 4.8% of 9939 and were input into “Input Analyzer” tool of Arena (Version 16.00.00002) and the transmission rate was found to follow a triangular distribution with lower limit, upper limit and mode being 0.51, 5 and 4.75 percentages respectively [31].
Contact network
The contact network plays a vital role in transmission dynamics. This includes i) contact rate estimation, ii) mapping the estimated contact rate in proportion with the population densities of various townships and iii) estimation of average contact rate based on proportion of various population densities. For contact rate estimation, we used a study from Ballabgarh, India, which, for a similar disease, to determine the age group distribution [31]. The contact rates of each group were found to follow normal distributions using “Input Analyzer” tool of Arena software (Table S3).
For population density related estimation, we used the Indian population classified based on types of towns that are presented in table S4 [32, 33]. The population density of Ballabgarh is 551 people per square kilometer [31]. This was used to proportionately determine the contact rates that would be obtained for various types of towns based on their respective population densities, assuming Density Dependent (DD) contact rate [34, 35].
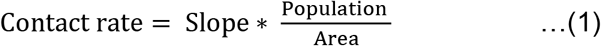
For estimation of average contact rate based on proportion of various population densities, the corresponding proportions of people from the sample size of the study in Ballabgarh were segregated and mapped to be living in Statutory town, Census town, Outgrowth and Village, respectively. The corresponding contact rates for these proportion(s) of people for each category of town were calculated based on the known contact rates (as in table S3) for Ballabgarh’s population density using the DD contact rate to population density proportion using the multiplication factor (table S4), which represents the ratio of the population density of a particular location type to the population density of Ballabgarh.
Table 1 indicates the contact rate distributions for each of the age groups. Number of people in each age group were divided further based on the proportion of people residing in each of the town type [32]. The number of contacts made by people under each age-town category were multiplied by their respective multiplication factors (table S4). These values were input to Arena and their respective contact rate distributions were determined using “Input Analyzer”. Lognormal distributions as mentioned in table-5 were obtained for contact rates, which represent those for the entire country. Natural log of the lognormal variables was determined, the parameters of which indicate the included normal values [36].
Contact rate distributions of various age groups (for India). Indicated are the parameters of Lognormal distributions: μ – mean of the included Normal; σ – standard deviation of the included Normal; Min – minimum sample (contact) value.
State chart
A state chart represents the various states in which an agent would exist, at any given instant [37]. Figure 1 represents the state chart for the disease model [18]. The initial state of all agents is defined to be healthy, as it is linked with the ‘start’ of the simulation. Once the simulation is run, an agent would be triggered to move to the ‘infected’ state randomly based on the probability i.e., he/ she is considered to acquire the infection. Further, based on the parameters assigned as per table 2, the agents would interact with other agents in the population and transmit the infection which is dependent on the number of contacts an agent interacts every day and the probability of an agent to get infected through contact, i.e., transmission rate. Agents in ‘infected’ state go through an incubation period from the time of exposure and turn out to be either symptomatic or asymptomatic. Agents continue to contact other agents and transmit till they either get ‘admitted’ after being ‘symptomatic’ or till they ‘recover’ being ‘asymptomatic’ for a defined time duration. Once admitted, all agents undergo treatment and either recover from the illness or move to serious illness condition and are taken to Intensive Care Unit (ICU) state. Upon further treatment, some patients recover after intensive care whereas a proportion of them turn critical and would require ‘ventilator’ support. Patients in this state either recover or are deceased after the treatment. Illness levels of patients during treatment tenure are categorized in three levels represented by ‘admitted’, ‘ICU’ and ‘ventilator’ states indicating severity of illness as illness, serious illness and critical illness respectively [22].
State chart for agent(s) (people)
Model calibration
Various parameters that are included in the model were determined based on various sources as discussed in this section. Models of Infectious Disease Agent Study (MIDAS) has also been used as a source of acquiring parameters through the pre-prints and manuscripts available [38]. Calibration of the model depicts the assignment of run parameters required for simulation that are mentioned in table 2 and also in points that follow.
Parameters for the model
References for parameters
WHO estimates that in India, about 80% of the cases remain asymptomatic or mild, 15% of the cases are severe and 5% cases require intense care and/ or ventilator assistance [43]. 50% to 75% were reported to be asymptomatic [44].
Recovered patients are not infected again and hence are excluded from further simulation process [45].
Transmission rate for all age groups follow a triangular distribution: Triangular(0.51, 4.75, 5)
Number of people who come in contact with an individual in the population follows a lognormal distribution as mentioned in table 1.
Hospital admission duration was determined to be 13 days with an Inter-quartile range (IQR) of (10–18) days for patients with no severity [17].
Time duration between exposure to discharge was 23 days with an IQR of (18–24.5) days [17].
Time duration of illness onset to discharge i.e., after the arrival of symptoms, was 18.5 days with an IQR of (15–22) days [17].
Incubation period was found to be 4 days with an IQR of (3–6) days. The longest incubation period was determined to be 14 days [17].
Time between illness onset to admission was 5 days [17].
Model scenarios
Once the model was developed and the parameters were assigned appropriately, the simulation was run for a duration of 365 days. The model was designed to trigger one infected agent (5–59 years) into the healthy population to understand the transmission dynamics and spread of infection based on the given parameters. In order to study the effect of minimization of number of contacts among the agents, three different scenarios were simulated and the results were compared, that are discussed in the subsequent sections. First scenario, referred to as “no lockdown” scenario can be comprehended as a routine day-to-day life as there were non-pharmaceutical interventions put in place from the day when the epidemic marked its onset in India [3]. The scenario contains three items. One is distancing second is the start date, third is duration. You need to mention all the three to describe a scenario. the parameters considered for the simulation of “no lockdown” scenario (scenario 1) are all based on the statistics obtained after the origination of the epidemic. Second and third scenarios considered 50% and 75% reductions in day-to-day contact among people, that are referred to as “50% lockdown” or “scenario 2” and “75% lockdown” or “scenario 3” respectively in this manuscript. The results of the simulation are discussed subsequently.
3. Results
Simulations were run for different age groups as per the categorization for all the three scenarios. Detailed day-wise data of the number of people in each of the state is provided in the supplementary excel file. The results of the same and their interpretations are discussed below.
Figures S1 a), 2 b) and 2 c) represent the number of healthy people on each day for the three different scenarios, respectively. In figures S1 a) and b), it is evident that the number of healthy people for the age groups less than 5 and above 60 decline well ahead of the age group between 5 and 59. It can be observed that during the peak infection days (table 3), for all the three scenarios, percentage of healthy people have declined to 34.62%, 58.69% and 82.87% of the initial healthy population respectively. It can be seen that there is a positive impact on the number of people remaining healthy due to the lockdown implemented. The peak infection for the three scenarios is found to occur on 105th, 172nd and 320th day of simulation run. For the 75% lockdown scenario, the peak decline has not been arrived at as is evident from the graph. This shows the delay that can be imposed on the crisis by stricter implementation of lockdown. For the age group of people above 60 years of age, the proportion of healthy people have declined to 1.34%, 18.04% and 93.65% respectively for the three scenarios. This age group is found to be affected the most in a no lockdown situation whereas the proportion of people infected is significantly reduced upon implementation of a 75% lockdown.
Figure S2 a) represents the number of healthy people on each day and it is clear that the rate of reduction in number of healthy people declines as the imposed lockdown percentage increases. After a duration of one year, proportion of people who remain healthy are 8.58%, 34.19% and 76.09% in the three scenarios signifying the impact created by the lockdowns imposed.
Figure S2 b) indicates the total number of people infected as on a chosen day. These results complement figure S2 a) owing to the fact that lockdown conditions hinder the rate of spread of the infection. The rate of spread of the infection is the minimum for the third scenario and is the maximum for scenario without any lockdown. Maximum number of people infected in scenarios 2 & 3 over a one year simulation run are 360834 and 131095 which would be reached in a period of just 106 and 81 days in a no lockdown condition.
Figure S2 c) represents the number of infections on a given day for all the three scenarios. These values reach a maximum of 146815, 61412 and 12583 which corresponds to 26.78%, 11.20% and 2.29% respectively of the initial population. A significant amount of reduction in peak infections is seen due to the lockdowns imposed. Furthermore, it is also noteworthy that there is a delay in the occurrence of these peak values as the stringency of the lockdowns imposed increases. These values which indicate the number of infections on a given day would be useful in determining the number of asymptomatic cases that remain unidentified given the number of identified and admitted cases. This technique could be useful to track and diagnose the contact networks of the people who are diagnosed to be positive. Significant proportion of asymptomatic cases remain a great challenge to the government and health care practitioners in tracking and treating the infected. It is also interesting to note that there were two peaks, one smaller and another bigger in no lockdown scenario and an attenuated peak for 50% lockdown, however in 75% lockdown this does not have a dual peak but slowly rises.
Figure S3 a) represents the number of asymptomatic people on each day indicating the peak values for the three different scenarios. The proportion of asymptomatic people is the highest for the age category ‘5 to 59’ which is around 80% of the total infected people. Number of asymptomatic carriers reach a peak value corresponding to 12.57%, 5.17% and 1.06% of the initial population respectively for the three scenarios. There is an occurrence of a local maximum equal to 40325 on 33rd day for no lockdown scenario and 4309 on 66th day for a 50% lockdown scenario. These local maxima are representations of the peak values that are observed due to the cumulative effect of peak infections among people aged below 5 years of age and people above 60 years of age. Asymptomatic carriers, being the ones to contact a greater number of people till their recovery are surely potential transmitters of the disease. They enhance the rate of spread till they have completely recovered, as they move freely unnoticed.
Figure S3 b) represents the number of people who would be in admitted state on each day. The peak values correspond to 12.61%, 3.03% and 0.48% of the initial healthy population respectively for the three scenarios. There is a considerable reduction in the peak values as the lockdown proportion is increased. The peak values provide a platform for hospital capacity planning to accommodate the number of admissions simultaneously.
Figure S3 c) indicates the number of people who move from normal illness to ICU on each day. The peak number of patients in ICU correspond to 1.12%, 0.2% and 0.03% of the initial healthy population respectively for the three scenarios. These percentages correspond to the peak values indicated in table 3 for each of the scenario which indicate the minimum number of intensive care setups required for the respective scenarios. These values are of serious concern to the healthcare providers as the arrangements for intensive care of patients have to be put in place with no delay. Most of the patients who require intensive care are projected to use ventilators. Hence, the peak numbers indicated in figure S3 d) (also in table 3) are of higher importance so as to assist patients with ventilators whenever required.
The peak values represented in figure S3 d) indicate the number of people who would require ventilator assistance on any given day. The peak values 5222, 1014 and 219 indicate the minimum number of ventilator setups required for each of the scenarios, as indicated in table 3 for each state represented by figure S3 d).
Figure S4 indicates the number of people deceased for various days. Higher mortality rate is seen for a no lockdown condition and it is seen to decline as the stringency of lockdown is increased. Number of people deceased after the model was simulated for 365 days are 4908, 3039 and 663 which correspond to 0.9%, 0.55% and 0.12% of the initial population respectively for three of the scenarios.
Table 3 indicates the peak values for various states possessed by the agents in the infection model. These values throw light on the timely measures to be taken to meet the peak demands at each of the scenario considered. The peak values also decrease for all these states as the stringency of lockdown is increased, indicating the effectiveness of lockdown measures. The values in % indicate the percentage contribution of each of the value for a particular state’s peak value when compared to the corresponding peak values of other two scenarios.
Peak values for various states of population
The peak number of infections is seen to decline by 15.58% and 24.49% (with initial healthy population as reference for 100%) respectively for 50% and 75% lockdown conditions compared to the no lockdown scenario. Likewise, there are drops across all states such as the peak number of admissions in ICU, peak number of patients requiring ventilators, and number of people deceased. A significant drop in peak number of ICUs required from 6115 for a no lockdown condition to 167 for a 75% lockdown is evident. Concurrently, the peak number of ventilators decline from 5222 for a no lockdown condition to 219 for a 75% lockdown condition.
4. Discussion
This approach based on the synthetic population of 5,43,823 agents for three different scenarios projects that the transmission rate of Covid-19 could be effectively brought down by stringency of lockdowns imposed. This is equivalent to pitching in non-pharmaceutical interventions into the model to reduce the number of contacts among people. The results of simulation model clearly indicated that the peak values of various states such as the number of infections, number of admissions in hospital, number of symptomatic/ asymptomatic cases, number of ICUs and ventilators required and number of people deceased could significantly be reduced by increasing the lockdown imposed. This might be helpful in flattening the curve. Thus, the importance of reducing the number of contacts, i.e., social distancing is apparent through the results of this study. There are several measures such as a ban on international travel, preventing inter-district and inter-state travel except for essentials and imposing a ban on even intra-district travel in hotspots/ epicenters of transmission would effectively reduce the rate of spread. Proportion of people who are deceased globally and went to critical illness were relatively higher for people aged above 60 owing to their adverse health conditions which are age dependent and comorbidities [10]. Transmission rates among children were also low as expected due to the fact that they are always sheltered by their parents and family members, which ultimately reduces their number of contacts with outside people.
Simulation outperforms analytical models for handling optimization of complex and dynamic systems [37]. A study employed Monte Carlo simulation to assess the transmission rate and reproduction number over time [15]. Another research study performed Bayesian analysis and found that the probability of misreporting Covid-19 in China was 48%. This might probably be due to the underestimation of the prevalence of virus or overestimation of mortality rates [46].
Though other mathematical and statistical modelling approaches have been used to project the epidemic in India and elsewhere, use of ABM in this study allowed us to clearly study the behaviour of agents depending on their characteristics. There are major differences among the widely used simulation models. DES mainly focusses on the flows of entities through various states/ processes of the system. There are no interactions between the entities of the system. System Dynamics concentrates on flows, stocks and delays. It focusses on collective measures rather than on measures pertaining to single/ group of agents. ABM is said to direct agents based on their parameters. This method also considers the interaction between agents whilst distinguishing them based on their individual parameters [47]. ABM approach was used over a population of 10,000 people; the study considered only four possible states an agent can take: susceptible, infected, sick, and immune [18]. Two of their three major assumptions include i) all infected people could be treated ii) close contacts could be reduced as soon as the first case is reported, which are rectified in the present study. ABM addresses micro-level interactions and heterogeneity among agents.
There are limitations of the current ABM approach. It does not consider the socio economic diversity of the population in the model. The network of agents has not been considered; however, we have used global estimates of contacts based on existing data from India and used a DD estimation based on population density. Considering high levels of clustering in contact networks, especially in the context of spread of infections would provide more accurate results [52–55]. The effects of forecasting Ebola through an ABM approach using a synthetic population with work/ school activity and mobility data of agents was examined [24]. An ABM approach was used in integration with GIS information to investigate the spread of epidemic in urban areas [21]. ABM consisting of a Euclidean complex network with agents moving on defined routes based on their schedules was performed [22]. The studies discussed above suggest that ABM provides a platform to integrate the GIS information to study the disease transmission dynamics. Other non-pharmaceutical interventions such as maintenance of face and hand hygiene, wearing protective face mask, etc. could be incorporated into the model to improve the accuracy and to study the effects of such activities on the infection transmission dynamics [56]. Exploring the contact network and dynamics of different regions would help us to represent the region-specific disease spread better. Also, including spatial data, ethnicity, gender, etc., into the model would allow obtaining region specific results. Wearable devices could be integrated with mobiles to provide real-time monitoring of Covid-19 patients and healthcare practitioners [57]. Also, these could possibly be integrated with applications that work based on geolocations to map infected areas/ people around.
5 Conclusions
We present an approach towards ABM using AnyLogic on a synthetic population. Further, data specific to India to parametrize such ABM will be critical. Having a synthetic population of a country can provide several options to create ABMs for several conditions apart from Covid-19 and may prove efficient for decision-making.
Data Availability
Detailed day-wise data of the number of people in each of the state, supplementary tables and supplementary figures used to support the findings of this study are included within the supplementary information file(s).
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this article.






